
Wir setzen unsere Bekanntschaft mit der sehr jungen, aber unglaublich schönen und mächtigen Programmiersprache Julia fort . Die sechsjährige Beta ist endlich beendet, sodass Sie jetzt keine Angst mehr vor Syntaxänderungen haben können. Und während sich alle streiten, ob es gut oder schlecht ist, mit der Indizierung zu beginnen, spielt die aufgeregte Community aktiv herum: Neue Bibliotheken kommen heraus, alte werden aktualisiert, ernsthafte Projekte beginnen und Studenten unterrichten diese Sprache aktiv an Universitäten. Lassen wir uns also nicht zurücklassen! Wir machen Tee stärker, weil wir diese Nacht codieren werden!
Vorbereitung auf die Arbeit
Hier gibt es eine kleine Rezension in russischer Sprache, auch auf dem Hub gibt es eine Kenntnis der Sprache und Installationsanweisungen . Auch hier wird es Probleme beim Herunterladen von Paketen geben, wenn man sich auf die Notwendigkeit des Windows Management Framework konzentriert .
Nach dem Upgrade enthält JuliaPRO nur noch Juno . Aber ich persönlich mag Jupyter mehr : Es gab keine Probleme mit dem Laptop, außerdem ist es praktisch, im Browser zu arbeiten und sofort Notizen und Formeln zu erstellen, im Allgemeinen ideal zum Erstellen von Berichten, Folien oder Handbüchern.
Heirate Jupyter und Julia 1.0.1 Es gibt mehrere Pakete für Julia, von denen die erfolgreichsten als Backends in den Plots enthalten sind. Plots.jl - Metasprache des Plots.jl : Plots.jl ist eine Schnittstelle für verschiedene Diagrammbibliotheken. Daher interpretiert Plots.jl Ihre Befehle nur und erstellt dann Diagramme mithilfe einer Diagrammbibliothek. Diese Hintergrundgrafikbibliotheken werden als Backends bezeichnet. Das Beste daran ist, dass Sie mit der Plots.jl Syntax viele verschiedene Grafikbibliotheken verwenden Plots.jl , und wir werden auch sehen, dass Plots.jl jeder dieser Bibliotheken neue Funktionen hinzufügt!
Installieren Sie GrafikpaketeFühren Sie zum Installieren von Paketen die Befehle in REPL, Juno oder Jupyter aus:
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
Es ist nicht erforderlich, alle Pakete zu installieren, aber Sie sollten wissen, dass jedes von ihnen seine eigenen Eigenschaften hat . Ich bevorzuge plotlyjs () : Obwohl es sich nicht in der Geschwindigkeit unterscheidet, ist es sehr interaktiv. Es gibt einen Zoom, der sich entlang der Ebene bewegt, sowie die Möglichkeit, die Datei zu speichern. Wenn Sie das Jupyter- Dokument als HTML speichern, werden alle Funktionen gespeichert. So können Sie der Site hinzufügen oder eine interaktive Präsentation erstellen. Weitere Informationen auf den Seiten: Plots , Gadfly
Endloses Primmuster
Umsetzung der Idee eines Artikels über Habr . In wenigen Worten: Was ist, wenn wir die Koordinate des Punktes nehmen und eine Operation verwenden, z. B. XOR oder bitweises UND zwischen der Abszisse und der Ordinate, und dann die Zahl auf Einfachheit oder Zugehörigkeit zu Fibonacci-Zahlen prüfen und wenn die Antwort Ja lautet, den Punkt mit einer Farbe füllen? und mit einem negativen in einem anderen? Überprüfen Sie:
Für den Betrieb% using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
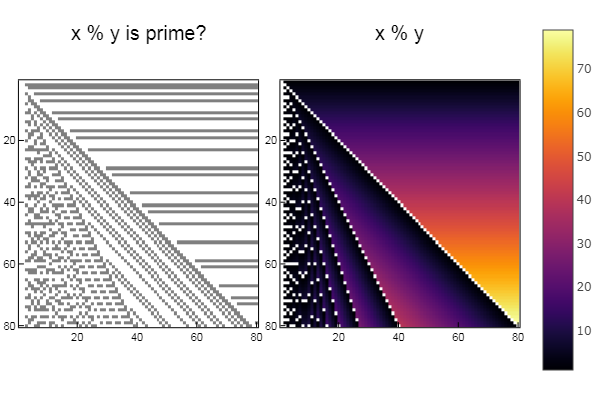
Für den Betrieb + W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
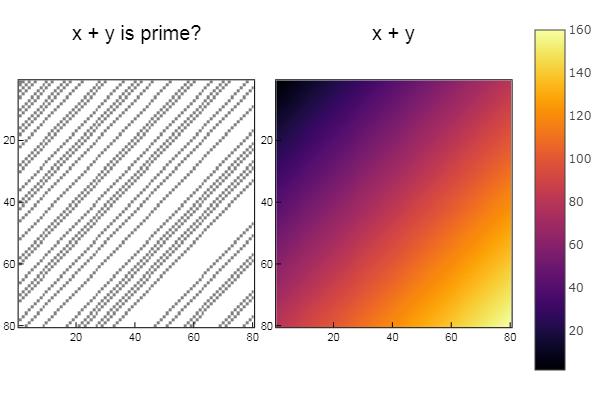
Für den Betrieb | W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

Für den Betrieb & W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
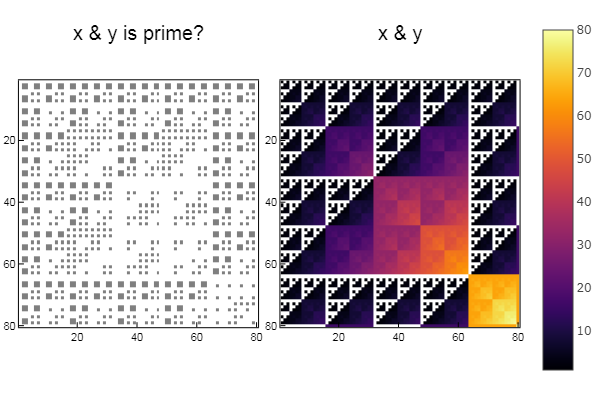
Für die Operation xor W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
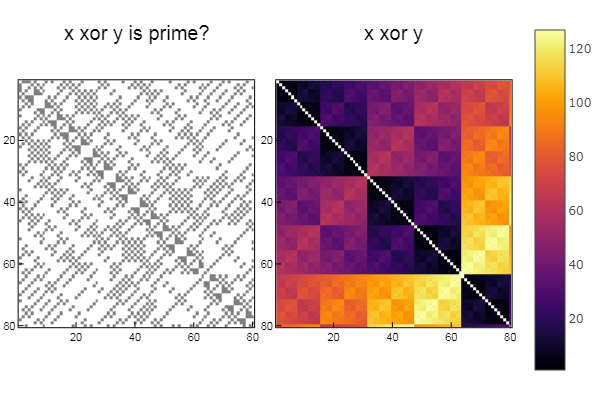
Und jetzt ist alles gleich, außer für Fibonacci-ZahlenSie können wie gewohnt eine Serie erstellen mit:
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
Verwenden wir jedoch die Matrixdarstellung ( genauer ):
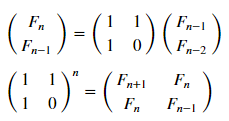
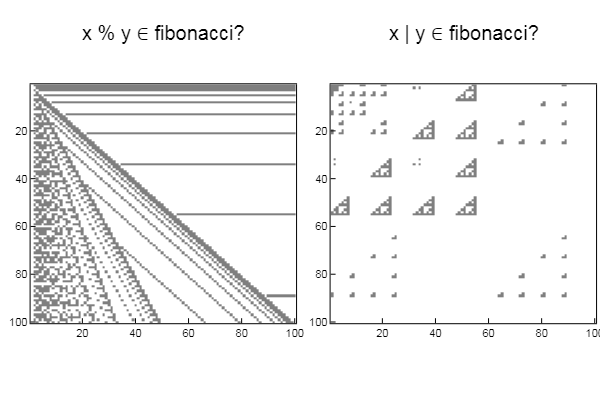
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
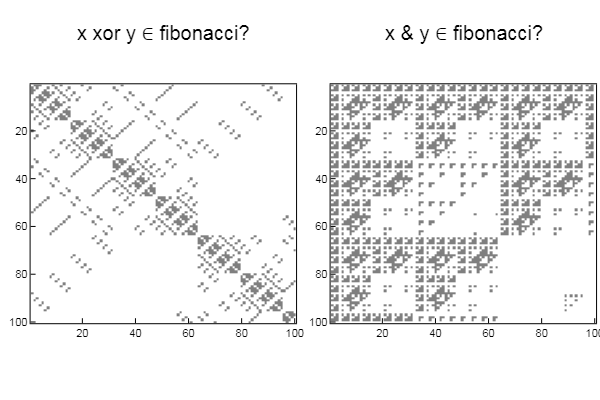
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
Reflexion einer Figur relativ gerade
Diese Art der Anzeige wird durch die Matrix bestimmt:
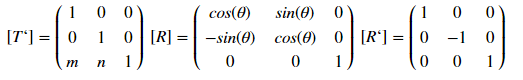
wobei [T '], [R] bzw. [R'] die Verschiebungs-, Rotations- und Reflexionsmatrizen sind. Wie funktioniert es Analysieren wir ein Beispiel für einen Versatz - für einen Punkt mit Koordinaten (x, y) wird der Versatz durch m um x und um n durch das Spiel durch die Transformation bestimmt:
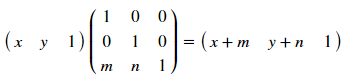
Diese Matrizen ermöglichen Transformationen für verschiedene Polygone. Die Hauptsache ist, die Koordinaten untereinander aufzuzeichnen und die Einheitsspalte am Ende nicht zu vergessen. Also [T]:
- verschiebt die Linie am Ursprung zusammen mit dem zu transformierenden Polygon
- dreht es so, dass es mit der X-Achse übereinstimmt
- spiegelt alle Punkte des Polygons in Bezug auf X wider
- gefolgt von Rückwärtsdrehung und Übertragung
Das Thema wird ausführlicher in dem Buch Rogers D., Adams J. Mathematische Grundlagen der Computergrafik beschrieben
Jetzt codiere es!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
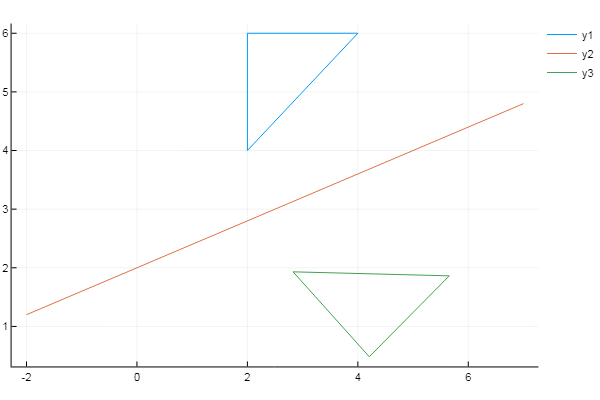
Interessante Tatsache: Wenn Sie griechische Zeichen loswerden und die erste Zeile durch ersetzen
function y=f(x,t) y=0.4*x + 2 endfunction,
Da die Klammern [] die Indizes der Arrays auf () und die Flöße auf dem plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ) umrahmen, läuft dieser Code so ziemlich in Scilab .
Arbeiten Sie mit dreidimensionalen Grafiken
Einige dieser Pakete unterstützen die Erstellung dreidimensionaler Diagramme. Ich möchte jedoch Makies ziemlich leistungsfähiges Visualisierungstool, das in Verbindung mit den GLFW- und GLAbstraction- Paketen funktioniert, die die OpenGL-Funktionen in Julia implementieren, separat erwähnen. Weitere Informationen zu Makie . Wir verstecken seine Zustimmung unter
Spoiler using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
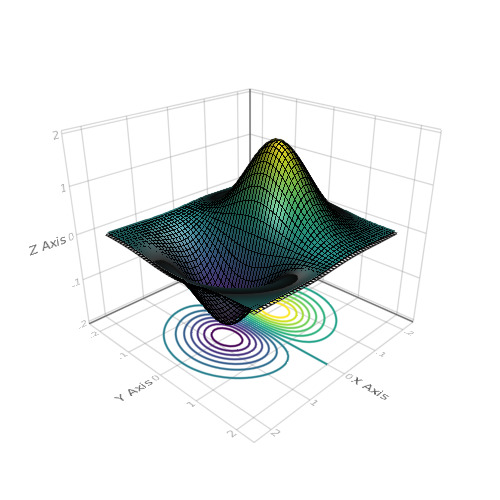
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
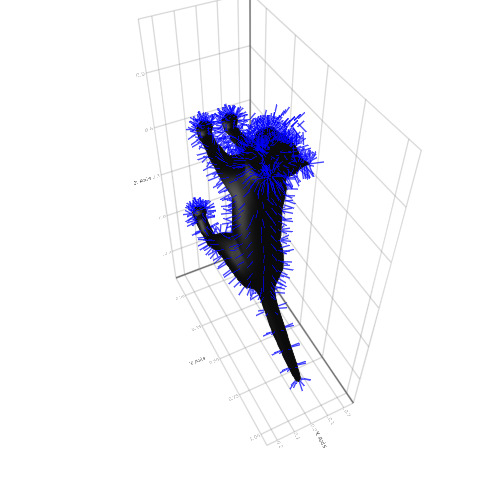
Das ist alles mit der Grafik. Interaktivität, Animation, 3D, Big Data oder schnelle Erstellung einfacher Grafiken - sich ständig weiterentwickelnde Pakete erfüllen nahezu jeden Geschmack und jede Anforderung. Darüber hinaus ist alles sehr einfach zu erlernen. Fühlen Sie sich frei, praktische Übungen herunterzuladen und Julia weiter zu verstehen!
UPD: Alle oben genannten Einträge werden in Jupyter mit Julia 0.6.4 erstellt. Leider wurden einige Funktionen des Plots-Metapakets entweder entfernt oder umbenannt, sodass wir weiterhin nach Updates suchen, aber der Spion wird vorerst vollständig ersetzt:
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)