Start gestartet
Das letzte Mal habe ich mich entschlossen, eine Tabelle mit Funktionswerten zu erstellen. Es ist an der Zeit, mit der Erstellung des Zeitplans selbst fortzufahren, für den all dies tatsächlich begann.
Die Hauptidee lautet also wie folgt. Drehen Sie die Koordinatenachse um 90 Grad im Uhrzeigersinn. Dies ist erforderlich, um die Konstruktion zu vereinfachen, ohne Daten zu jedem Punkt in einem Blatt zu speichern.
Als nächstes beschränken wir die Koordinatenachse des Spiels auf 82 Zeichen, um die Lesbarkeit des Diagramms zu verbessern. Es ist klar, dass wir dadurch an Genauigkeit verlieren und der Zeitplan schematischer (zu eng) sein wird, insbesondere für „coole“ Funktionen, aber immer noch.
Danach berechnen wir die Position der x-Achse relativ zur Achse der Spieler, dh wir suchen, an welcher Stelle wir einen Punkt haben (x, 0). Nun, dann werden wir zeilenweise x den Wert der Funktion y1 an dieser Stelle zuweisen.
Lass uns gehen
Zunächst benötigen wir die folgende Formel:
Wir werden dem Zeitplan selbst 80 Positionen zuweisen, die beiden verbleibenden Plätze werden rein dekorativ sein. Mit dieser Formel finden wir heraus, welcher Wertebereich einer Position in unserem Diagramm entspricht. Dann können wir den aktuellen Punkt darauf korrekt markieren.
Die Hauptideen werden umrissen. Fahren wir also mit dem Code selbst fort
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Dank der Kommentare zum ersten Teil habe ich so etwas wie
Format gelernt. Es schien mir wirklich bequemer als meine Tänze mit einem Tamburin, also verwandelte sich ein riesiger Code aus der Berechnung von Einrückungen in ein paar Zeilen
print("{1:>{0}}".format(len(label) + dial_length, label), '\n')
Die Einheit ist für die Nummer des Elements verantwortlich, das als Argument an die Formatierungsfunktion übergeben wird, dh es handelt sich um eine „Verknüpfung“ (nicht wörtlich) mit der Beschriftungsvariablen, die wir tatsächlich auf dem Bildschirm anzeigen. Die Nummerierung erfolgt genauso wie in den Blättern - von Grund auf neu.
Ein Zeichenpaar
:> wird verwendet, um den angezeigten Text auf der rechten Seite auszurichten. Nun,
{0} nach dem Zeichen
> wird benötigt, um die Anzahl der benötigten Zeilenpositionen zu bestimmen.
Das heißt, in diesem Fall behalten wir uns die Positionen für die Zeilenbezeichnung len (label) + dial_length vor, und die Beschriftung selbst nimmt nur len (label) ein, und wir richten den Text auf der rechten Seite innerhalb des Satzes dieser Positionen aus.
print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print(dial_length*' ' + label, '\n')
Diese Zeilen sind äquivalent
Ja, für Zeichenfolgen ist es wahrscheinlich einfacher, die zweite Option zu verwenden, aber die erste für die allgemeine Entwicklung anzuwenden, schadet nicht.
print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Sogar Arrays vom Typ r_value (in C ++) können in ein Format gepackt werden, das direkt beim Übergeben eines Arguments erstellt wird.
Wir fixieren die Variablen, die bei uns konstant sind, dh sie hängen nicht vom aktuellen Wert der Funktion ab.
In Python gibt es keine bedingte Konstante für die Bezeichnung von Konstanten. Daher ist es üblich, solche Variablen in Großbuchstaben aufzurufen und sie einfach nicht zu ändern.
MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81
Da RATIO aus offensichtlichen Gründen nicht gleich 0 sein kann, sollte MAX_Y1_VALUE_DIFFERENCE eine positive Zahl sein. Deshalb befindet sich die zweite Amtszeit auf der rechten Seite der Aufgabe.
Die Position der x-Achse berechnen wir nach der Formel
Woher kommt diese Formel? Wir berechnen einfach das Verhältnis der Segmente (auf der Achse des Spiels) vom Anfang der Achse (min (y1)) zum aktuellen Wert der Funktion (y1 (x)) und des Segments vom Anfang der Achse bis zu ihrem Ende (max (y1)). Nun, wir multiplizieren dieses Verhältnis mit 80, um den Abstand vom Anfang der Achse zum aktuellen Wert in Räumen zu ermitteln (daher können Sie nur ganze Zahlen verwenden), der die Verhältnisformel im Diagramm widerspiegelt.
Da wir an der Position bei y1 (x) = 0 interessiert sind, setzen wir die notwendigen Werte und voila in die Formel ein.
Jetzt können Sie direkt zum Drucken von Werten übergehen
while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE)
Der Zyklus ist uns bereits bekannt. Wir müssen jeden Wert der Funktion ein zweites Mal zählen, um sie nicht in einem Blatt oder etwas anderem zu speichern.
Die Position des Spiels wird nach der obigen Formel berechnet.
Wir müssen den oberen Unterschied zur Formel korrigieren, vorausgesetzt, wir erhalten in der Formel die Unsicherheit der Form Null durch Null. Wenn eine solche Unsicherheit auftritt, bedeutet dies, dass der aktuelle Wert y1 (x) = max (y1) ist, was bedeutet, dass der aktuelle Wert des Spiels mit dem Ende der y-Achse übereinstimmt.
print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Dieser Teil des Codes ist direkt für das Drucken des Diagramms selbst verantwortlich.
print("{1:^{0}.6g}".format(dial_length, from_x), end='')
Hier war das Format sehr nützlich und vereinfachte den Code.
^ ermöglicht es uns, die Zahl in der Mitte des ausgewählten Bereichs auszurichten (in diesem Fall 12 Positionen).
g ist für Zahlen verantwortlich - wenn sie keinen Bruchteil haben, wird er nicht gedruckt (Zahl als int), andernfalls - 6 Dezimalstellen
Da unser Diagramm auf einen Abstand von 80 Zeichen entlang der y-Achse beschränkt ist, stimmt der Wert der Funktion am Punkt in unserem Diagramm nicht nur mit der x-Achse überein, wenn y1 (x) = 0 ist, sondern auch in der Nachbarschaft [0 - RATIO / 2, 0 + RATIO / 2].
Insgesamt haben wir drei Fälle, in denen sich das Sternchen (dh der Punkt) und der vertikale Stick (dh die x-Achse) befinden: '* |' (y1 (x) <= 0 - VERHÄLTNIS / 2), '*' (0 - VERHÄLTNIS / 2 <y1 (x) <0 + VERHÄLTNIS / 2), '| *' (y1 (x)> = 0 + VERHÄLTNIS / 2) werden wir diese drei Fälle betrachten.
- y1 (x) <= 0 - VERHÄLTNIS / 2
In diesem Fall befindet sich der Punkt auf der x-Achse, daher suchen wir den Abstand vom Punkt zur Achse in Räumen. Aufgrund der Rundung von Zahlen kann es vorkommen, dass die Werte der Variablen AXIS_X_POS und pos_of_y übereinstimmen. Dies kann aber nicht sein, da wir in diesem Fall im dritten Fall wären. In unserem Fall stimmt der Punkt nicht mit der x-Achse überein, daher ist eine zusätzliche Bedingung erforderlich, die bei Gleichheit die Variable pos_of_y um 1 reduziert. - y (x)> = 0 + VERHÄLTNIS / 2
Der Fall ist identisch mit dem ersten Fall, nur der Punkt befindet sich auf der anderen Seite der x-Achse und alle oben genannten Aktionen werden dafür angepasst - der Rest
Der einfachste Fall - drucken Sie einfach ein Sternchen anstelle der Achse
Das heißt, wenn wir negative Werte haben (y1 (x) <0). Wenn nicht, geben Sie einfach '|' ein und bestimmen Sie die Position des Punktes.
Nun, wir beenden das Programm mit einer zusätzlichen x-Achse.
Also, der Code, der endete:
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:^{0}.6f}".format(dial_length, x_copy)) print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 81, 'y' , 82*'-']), end=''); MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81 while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE) print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Führen Sie das Programm in mehreren Tests aus
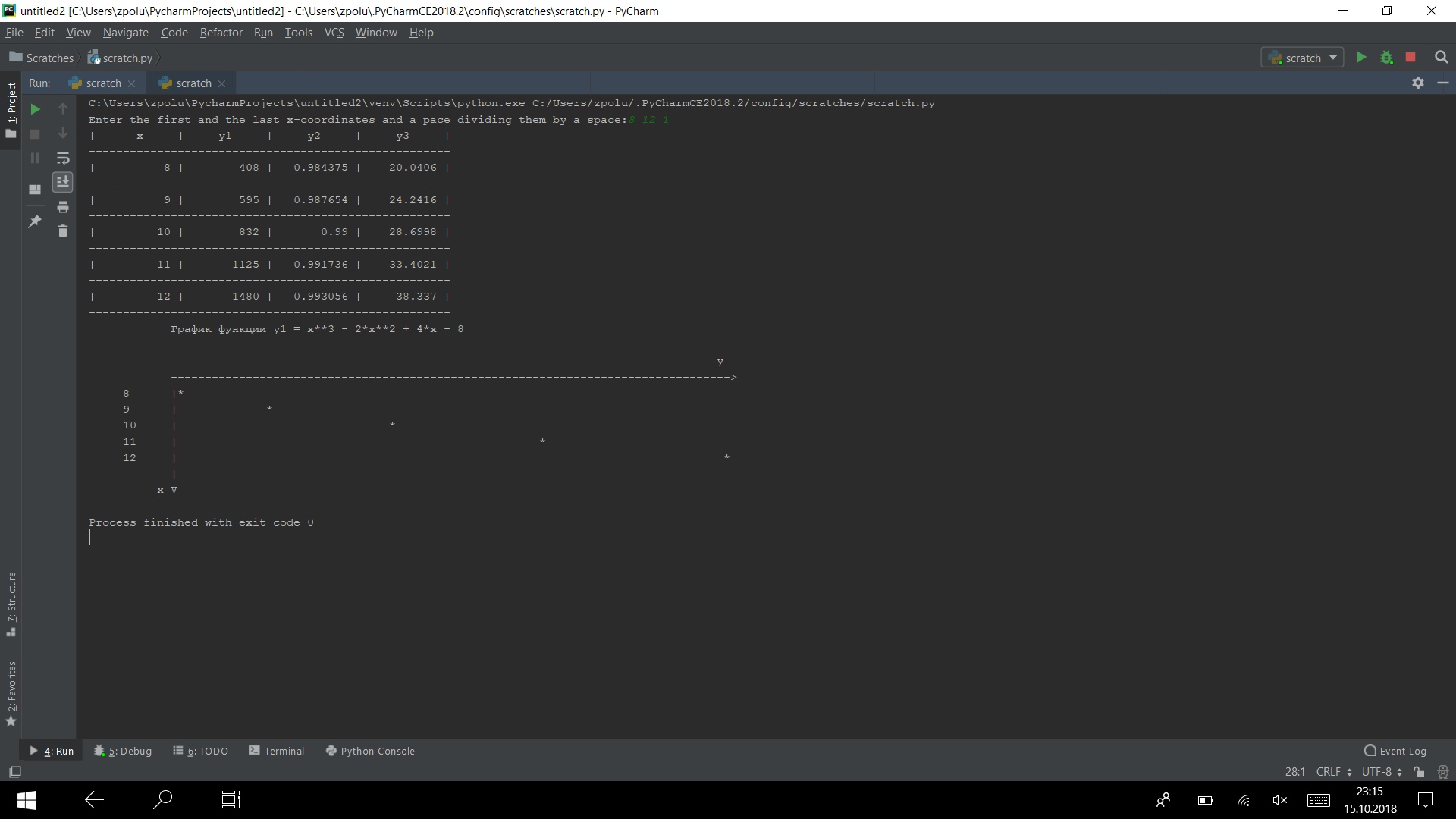
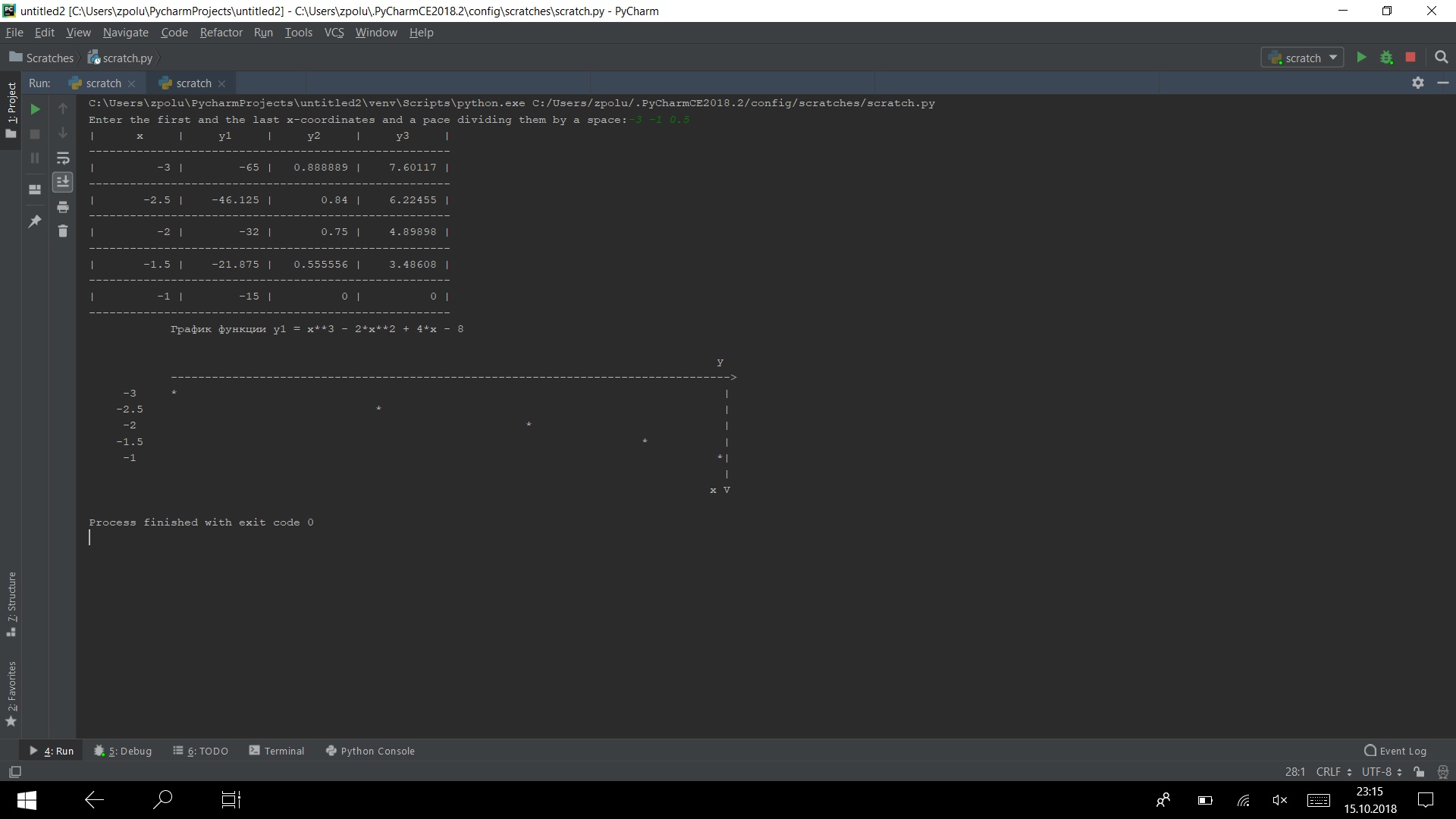
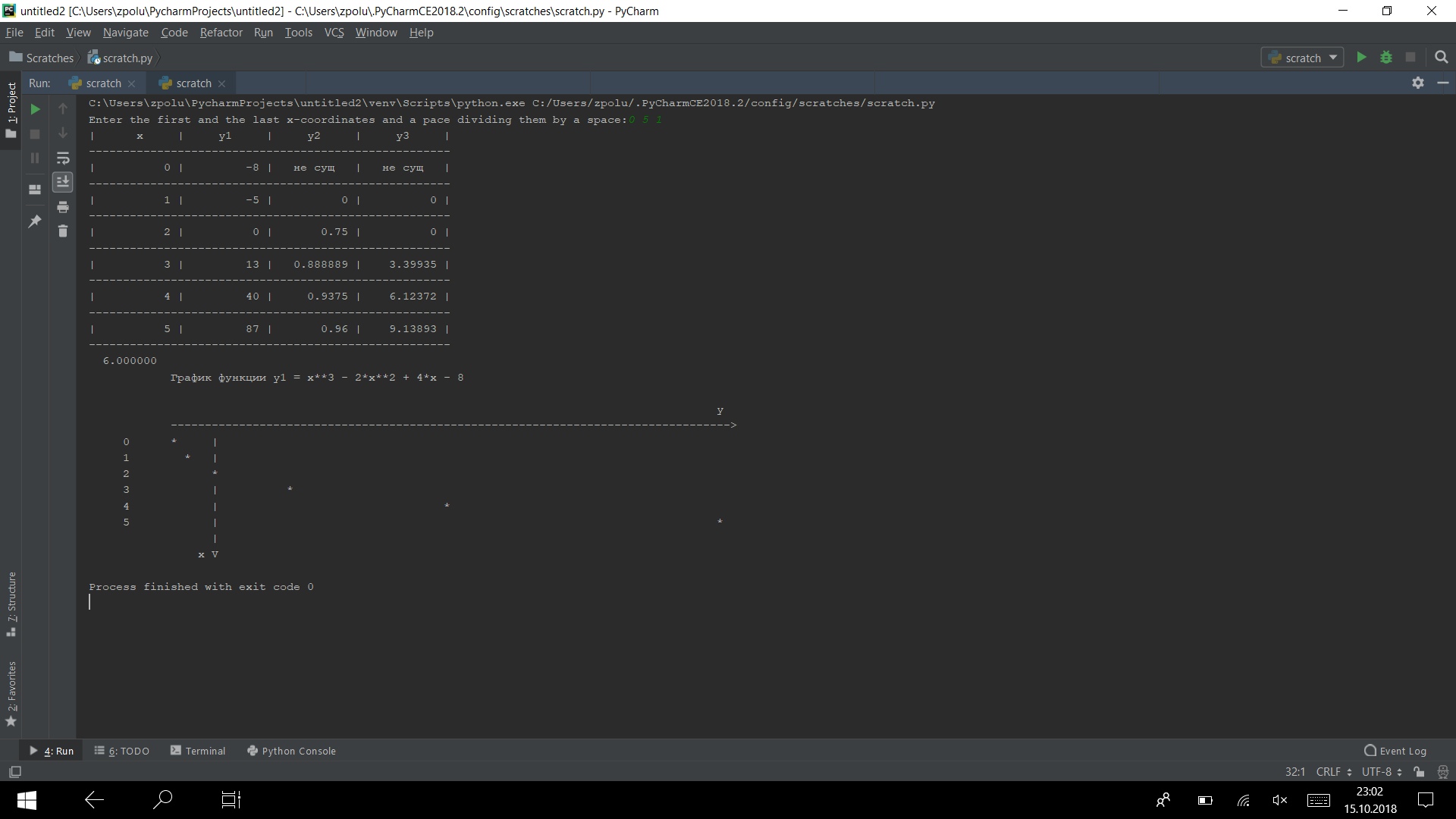
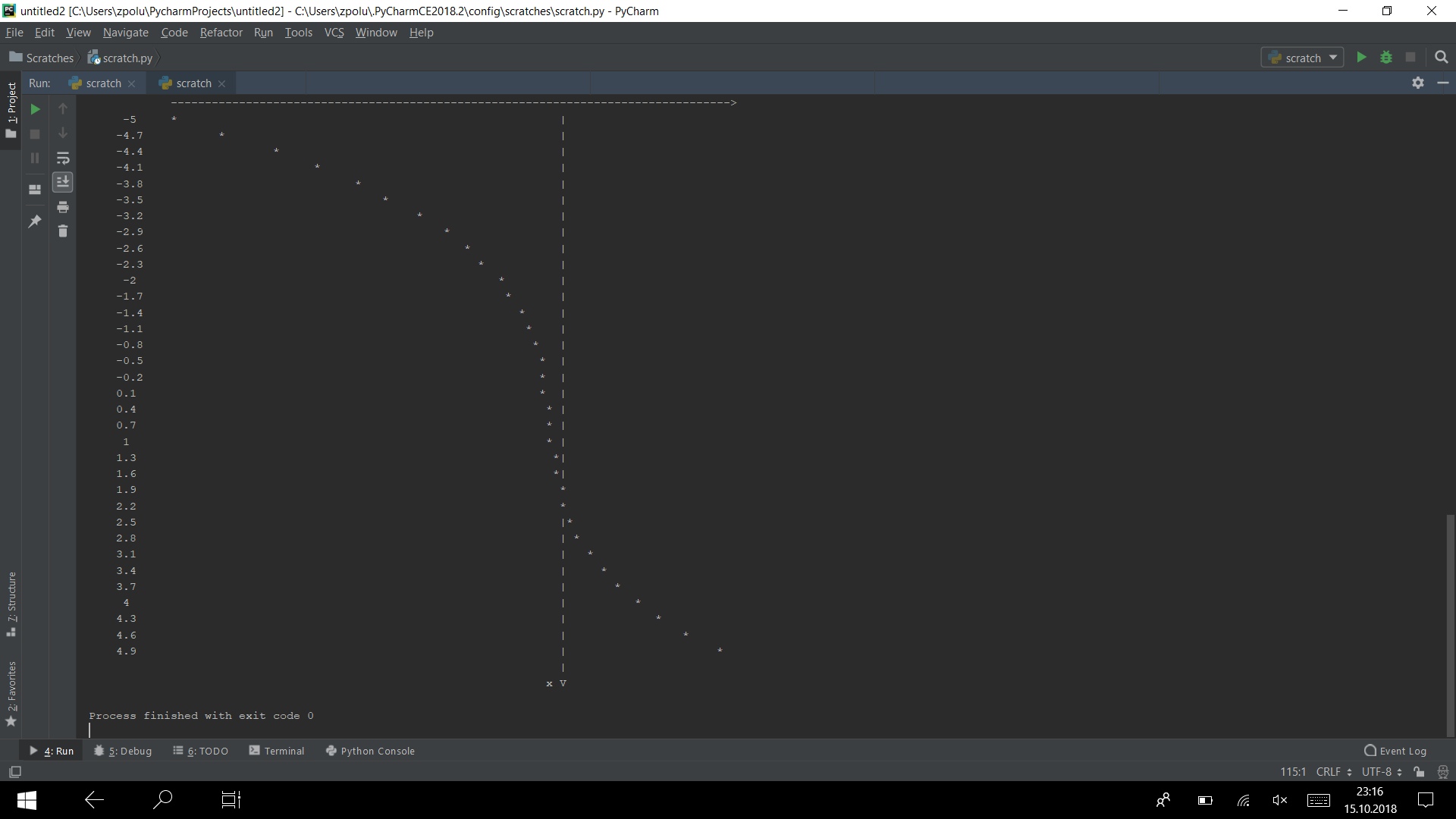
Es funktioniert)
