Spinnspirale: Mathematik und Halluzinationen

Bei dem Versuch, sich Halluzinationen vorzustellen, die durch Betäubungsmittel verursacht werden, fallen wirbelnde, spiralförmige psychedelische Formen ein, die unmittelbar dem Tunnelblick ähneln. Solche geometrischen Strukturen können jedoch nicht nur halluzinogene Medikamente wie LSD, Cannabis oder Meskalin verursachen . Die Menschen sprachen über das Auftreten solcher Visionen zu der Zeit, als sie im Tod waren, unter so schmerzhaften Zuständen wie Epilepsie und Schizophrenie, als Folge sensorischer Deprivation oder sogar nach einfachem Druck auf die Augäpfel. Solche geometrischen Halluzinationen sind so weit verbreitet, dass sich Wissenschaftler im letzten Jahrhundert fragten, ob sie uns etwas Grundlegendes über die Struktur unseres Gehirns erzählen könnten. Und anscheinend ist es das auch.


Auf einem Computer erstellte Formularkonstanten. Die beiden oberen Bilder ahmen den Trichter und die Spirale nach, die nach dem Empfang von LSD auftreten. Unten links ist die von Marihuana erzeugte Wabe. Unten rechts ist das Web.

Systematische geometrische Halluzinationen wurden erstmals in den 1920er Jahren von einem amerikanisch-deutschen Psychologen, Heinrich Kluver, untersucht . Kluvers Interesse an visueller Wahrnehmung führte ihn schließlich dazu, mit Peyote zu experimentieren, einem Kaktus, der von Carlos Castaneda gefeiert wurde, dessen psychoaktiver Bestandteil Meskalin eine wichtige Rolle in den schamanistischen Ritualen vieler zentralamerikanischer Stämme spielte. Meskalin ist bekannt dafür, lebhafte visuelle Halluzinationen zu verursachen. Kluver benutzte Peyote im Labor mit einem Assistenten und bemerkte, dass sich geometrische Formen in durch Meskalin verursachten Halluzinationen wiederholten. Er teilte sie in vier Typen ein und nannte sie Konstanten : Tunnel und Trichter, Spiralen, Gitter, einschließlich Waben und Dreiecke, sowie Spinnweben.

In den 1970er Jahren verwendeten die Mathematiker Jack Cowan und Bard Ermentraut Kluvers Klassifikation, um eine Theorie zu erstellen, die beschreibt, was im Gehirn passiert, wenn wir glauben, dass wir geometrische Muster sehen. Ihre Theorie wurde von anderen Wissenschaftlern weiterentwickelt, darunter Paul Breslov, Professor für mathematische und rechnergestützte Neurobiologie am kürzlich gegründeten Oxford Centre for Collaborative Applied Mathematics.

Wo sind die Streifen von der Großhirnrinde *

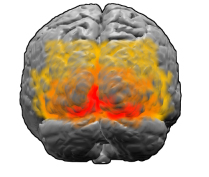Der visuelle Kortex. Rot markierter Bereich V1

[ * Hinweis auf das vietnamesische Märchen „Woher kommt der Tiger vom Streifen?“ / Ca. perev. ]]

Der erste Bereich des visuellen Kortex des Gehirns, der Bilder bei Menschen und Säugetieren verarbeitet, ist der als V1 bekannte Bereich. Experimentelle Beweise wie fMRI- Bilder legen nahe, dass Kluver-Muster ebenfalls größtenteils aus V1 stammen und später nicht irgendwo im visuellen System erscheinen. Wie der Rest des Gehirns hat V1 eine komplexe, faltige, gefaltete Struktur - es gibt jedoch eine überraschend einfache Möglichkeit, das, was wir in unserem Sichtfeld sehen, in die Aktivität von Neuronen in V1 zu übersetzen. "Stellen Sie sich vor, wir setzen V1 ein", sagt Breslov. - Man kann es sich als mehrere Millimeter dickes Nervengewebe mit verschiedenen Schichten von Neuronen vorstellen. In erster Näherung verhalten sich Neuronen in der gesamten Tiefe des Kortex ähnlich. Wenn Sie sie also abflachen, können Sie sich V1 als zweidimensionales Blatt vorstellen. "

Das Objekt oder die Szene der visuellen Welt wird in Form eines zweidimensionalen Bildes auf die Netzhaut jedes Auges projiziert, sodass das, was wir sehen, auch als flaches Blatt betrachtet werden kann: Sichtfeld. Jeder Punkt auf diesem Blatt kann durch zwei Koordinaten gekennzeichnet werden, z. B. einen Punkt auf der Karte oder einen Punkt auf einem flachen Modell V1. Die abwechselnden hellen und dunklen Bereiche, aus denen die geometrischen Halluzinationen bestehen, werden durch die abwechselnden Bereiche mit hoher und niedriger Aktivität von Neuronen in V1 verursacht - Bereiche, in denen Neuronen sehr schnell aktiviert werden, und Bereiche, in denen das Gegenteil der Fall ist.

Um visuelle Muster in Neuronenaktivität zu übersetzen, ist ein Koordinatengitter erforderlich - eine Regel, nach der jeder Punkt des Sichtfelds mit einem Punkt des Ebenenmodells V1 verbunden ist. In den 1970er Jahren erstellten Wissenschaftler, darunter auch Cowen, ein solches Raster, das auf der Kenntnis der Anatomie der Interaktion von Netzhautneuronen mit Neuronen in V1 beruhte. Für jeden hellen oder dunklen Teil des Sichtfelds definiert die Abbildung einen Teil hoher oder niedriger neuronaler Aktivität in V1.

Wie transformiert diese Abbildung der Netzhaut und des Kortex die geometrischen Muster von Kluver? Es stellt sich heraus, dass Halluzinationen, die Spiralen, Kreise und Strahlen verursachen, die vom Zentrum ausgehen, den Aktivitätsstreifen von Neuronen in V1 entsprechen, die in bestimmten Winkeln verlaufen. Gitter wie Waben oder Zellen entsprechen den hexagonalen Aktivitätsmustern in V1. Dies mag an sich nicht so interessant sein, aber es gibt einen Präzedenzfall: Es waren die Streifen und Sechsecke, die Wissenschaftler bei der Modellierung anderer Beispiele für die Bildung von Mustern beobachteten, beispielsweise die Konvektion von Flüssigkeiten oder überraschenderweise das Auftreten von Flecken und Streifen auf Tierhäuten. Die Mathematik zur Bildung dieser Muster war bekannt und schlug auch einen Mechanismus zur Modellierung der Funktionsweise des visuellen Kortex vor.

Vom Sichtfeld zum visuellen Kortex

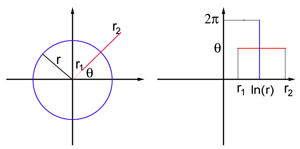
Stellen Sie sich das Sichtfeld in Form eines flachen Blattes mit Polarkoordinaten vor: Jeder Punkt P wird durch zwei Zahlen (r, θ) definiert, wobei r der Abstand zum Ursprung und θ der Winkel zwischen dem Segment OP und der x-Achse ist. Der Bezugspunkt entspricht der Mitte des Sichtfeldes. V1 wird ebenfalls als flaches Blatt modelliert, diesmal jedoch mit kartesischen Koordinaten (x, y). Die genaue Koordinatenanzeige des Sichtfelds und des Ebenenmodells V1 ist für diesen Artikel zu kompliziert, aber für Punkte, die weit genug von der Mitte des Sichtfelds entfernt sind (dh für ein ausreichend großes r), ähnelt es einer logarithmischen Karte:

$$

$$x = \ ln {r} \\ y = \ theta$$

Die Abbildung übersetzt einen Kreis mit dem Radius r im Sichtfeld in ein gerades vertikales Segment mit x = ln r und einen Strahl, der vom Ursprung der Koordinaten O unter einem Winkel θ kommt, in ein gerades horizontales Segment mit y = θ

Woher kommt der Leopard?

Das erste Modell zur Bildung von Tierhautmustern stammt von Alan Turing , besser bekannt als der Vater der modernen Informatik und ein Hacker aus Bletchley Park, der Codes geknackt hat. Turing war daran interessiert, wie ein so räumlich homogenes System wie ein einheitlicher Zellball, der der Embryo des Tieres ist, räumlich inhomogene, aber statische Muster wie Zebrastreifen erzeugen kann.

Turing schlug vor, dass diese Muster als Ergebnis eines Reaktionsdiffusionsprozesses auftreten . Stellen Sie sich einen tierischen Embryo vor, in dessen Haut zwei chemische Verbindungen leben. Einer von ihnen ist ein Inhibitor, der die Produktion von sich selbst und einer anderen Chemikalie unterdrückt. Der andere ist ein Katalysator, der die Produktion beider Substanzen bewirkt.

Im ersten Moment des Turing-Modells gleichen sich zwei Chemikalien idealerweise aus - sie befinden sich im Gleichgewicht und ihre Konzentration an verschiedenen Punkten des Embryos ändert sich nicht mit der Zeit. Stellen Sie sich nun vor, dass aus irgendeinem Grund die Katalysatorkonzentration irgendwann leicht anstieg. Diese leichte Störung setzt das gesamte System in Bewegung. Die erhöhte lokale Konzentration des Katalysators bedeutet, dass dort mehr Katalysator und Inhibitor produziert werden. Beide Verbindungen diffundieren jedoch auch über die Haut des Embryos und hemmen und katalysieren ihre Produktion an anderen Stellen.

Wenn beispielsweise ein Inhibitor schneller diffundiert als ein Katalysator, umgibt er schnell den Störungspunkt und verringert die Konzentration des Katalysators darin. Als Ergebnis erhalten wir einen Abschnitt mit einer hohen Katalysatorkonzentration, umgeben von einer hohen Inhibitorkonzentration - mit anderen Worten, einem Katalysatorfleck auf dem Hintergrund des Inhibitors. Abhängig von der Diffusionsrate der beiden Verbindungen ist es möglich, dass ein solches Fleckenmuster auf der Haut des Embryos auftritt und sich schließlich stabilisiert.

Thuring schrieb ein System von Differentialgleichungen auf, das die Konkurrenz zwischen den beiden Verbindungen beschreibt - Sie können sie sich rechtzeitig entwickeln lassen und sehen, ob Muster auftreten. Diese Gleichungen hängen von Parametern ab, die die Diffusionsrate zweier Verbindungen beschreiben: Wenn Sie sie richtig auswählen, stabilisiert sich das System schließlich und bildet ein bestimmtes Muster, das durch Ändern der Parameter geändert werden kann. Der Link bietet ein Applet in Java , in dem Sie mit den Parametern herumspielen und die resultierenden Muster anzeigen können.

Gleichungen von Tiermustern

Stellen Sie sich der Einfachheit halber einen Embryo in Form einer eindimensionalen Linie vor. Zu jedem Zeitpunkt t und zu jedem Zeitpunkt x des Embryos wird die Konzentration des Katalysators (Aktivators) und des Inhibitors (Inhibitors) durch die Funktionen A (x, t) und I (x, t) bestimmt. Sie ändern sich im Laufe der Zeit nach folgenden Regeln:

$$

$$\ frac {\ partielles A} {\ partielles t} = f (A, I) + \ frac {\ partielles ^ 2 A} {\ partielles x ^ 2} \\ \ frac {\ partielles I} {\ partielles t } = g (A, I) + d \ frac {\ partiell ^ 2 I} {\ partiell x ^ 2}$$

Der erste Term rechts von jeder Gleichung beschreibt die Menge der Katalysator- und Inhibitorproduktion. Sie sind Funktionen der Konzentrationen von Katalysator und Inhibitor, da beide die Reaktionsgeschwindigkeit beeinflussen.

Der zweite Term rechts von jeder Gleichung ist die zweite Ableitung, die die Änderungsrate des Gradienten des Katalysators und des Inhibitors beschreibt. Sie stellen die Diffusionsrate ein.

Ein zusätzlicher Term d auf der rechten Seite der zweiten Gleichung ist der Diffusionskoeffizient, der zeigt, wie stark der Inhibitor schneller diffundiert als der Katalysator. Turing hat gezeigt, dass die Überlegenheit der Inhibitorgeschwindigkeit ein kritischer Parameter für die Fleckenbildung ist.

Gehirnmuster

Die Aktivität von Neuronen im Gehirn ist kein reaktionsdiffuser Prozess, weist jedoch Analogien zum Turing-Modell auf. „Neuronen senden Signale über Datenausgangskanäle, sogenannte Axone, aneinander“, sagt Breslov. Neuronen reagieren auf die Signale des anderen, hier ist die Reaktion. "Signale bewegen sich im Vergleich zum Strukturierungsprozess so schnell, dass sie für sofortige Interaktionen gehalten werden können." Anstelle von Diffusion, einem lokalen Prozess, haben wir daher eine sofortige Interaktion in der Ferne. Die Rolle von Katalysator und Inhibitor spielen zwei verschiedene Klassen von Neuronen. "Es gibt exzitatorische Neuronen - die die Wahrscheinlichkeit erhöhen, dass andere Neuronen aktiv werden - und es gibt inhibitorische Neuronen, die diese Wahrscheinlichkeit verringern", sagt Breslov. "Die Konkurrenz zwischen den beiden Klassen von Neuronen ist analog zum Katalysator-Inhibitor-Mechanismus im Turing-Modell."


Gestreifte, hexagonale und rechteckige Muster der Nervenaktivität in V1, die durch ein mathematisches Modell erzeugt wurden

Inspiriert von den Analogien der Turing-Prozesse erstellten Cowan und Ermentraut ein Modell der Nervenaktivität in V1 unter Verwendung eines von Cowan und Hugh Wilson formulierten Gleichungssystems. Obwohl sich herausstellte, dass die Gleichungen komplizierter waren als die von Turing, können Sie immer noch dasselbe Spiel spielen und das System im Laufe der Zeit weiterentwickeln lassen, um festzustellen, ob sich Muster nervöser Aktivität entwickeln. „Wenn Sie unter bestimmten Bedingungen den Parameter erhöhen, der beispielsweise die Wirkung von Arzneimitteln auf den Kortex darstellt, führt dies unter bestimmten Bedingungen zum Wachstum periodischer Muster“, sagt Breslov.

Das Cowan- und Ermentraut-Modell legt nahe, dass geometrische Halluzinationen auf Instabilität in V1 zurückzuführen sind: Etwas, beispielsweise das Vorhandensein des Arzneimittels, entfernt das neuronale Netzwerk aus einem ausgeglichenen Zustand und startet einen Schneeball-Wachstumsprozess der Interaktion zwischen anregenden und unterdrückenden Neuronen, der sich dann stabilisiert in Form von gestreiften oder hexagonalen Mustern der Nervenaktivität in V1. Dann „beobachten“ wir dieses Muster in Form von geometrischen Strukturen, die Kluver im Sichtfeld beschreibt.

Symmetrien im Gehirn

Tatsächlich ist nicht alles so einfach wie im Cowan- und Ermentraut-Modell, da Neuronen nicht nur auf helle und dunkle Bilder reagieren. Durch die Dicke V1 reihen sich Neuronen in Spalten an, die als Hypersäulen bekannt sind , von denen jede ungefähr auf einen kleinen Teil des Gesichtsfeldes reagiert. Aber nicht alle Neuronen in der Hypersäule sind gleich: Zusätzlich zum Erkennen der hellen und dunklen Bereiche ist jedes Neuron darauf spezialisiert, lokale Gesichter zu erkennen - Linien, die helle und dunkle Bereiche in einem Teil des Bildes trennen - eine bestimmte Ausrichtung. Einige erkennen horizontale Flächen, andere - vertikale, andere - Flächen, die sich in einem Winkel von 45 ° befinden, und so weiter. Jede Hypersäule enthält Spalten von Neuronen aller bevorzugten Orientierungen, daher kann eine Hypersäule auf die Flächen aller Orientierungen in einem bestimmten Bereich des Gesichtsfelds reagieren. Es ist die Zusammensetzung von Hypersäulen und Orientierungspräferenzen, die es uns ermöglicht, die Konturen, Oberflächen und Texturen der visuellen Welt zu erkennen.


Verbindungen in V1: Neuronen in einer Hypersäule interagieren mit den meisten anderen Neuronen. Sie reagieren jedoch nur dann mit Neuronen in anderen Hyperkolonnen, wenn sich die Säulen in Richtung ihrer Orientierung befinden und die Neuronen dieselbe Orientierungspräferenz haben.

In den letzten Jahren wurden zahlreiche anatomische Belege dafür gesammelt, wie Neuronen mit unterschiedlichen Orientierungspräferenzen miteinander interagieren. Innerhalb ihrer Geosäule interagieren Neuronen mit den meisten anderen Neuronen, unabhängig von ihren Vorlieben. Die Neuronen anderer Hypersäulen wirken jedoch selektiver und interagieren nur mit Neuronen ähnlicher Präferenzen, um uns die Fähigkeit zu garantieren, kontinuierliche Konturen in der visuellen Welt zu erkennen.

Breslov verallgemeinerte zusammen mit Cowen, dem Mathematiker Martin Golubitsky und anderen Wissenschaftlern das ursprüngliche Modell von Cowen und Ermentraut, um diese neuen anatomischen Beweise zu berücksichtigen. Sie verwendeten die Ebene erneut als Grundlage für das V1-Modell: Jede Hypersäule wird in der Ebene durch einen Punkt (x, y) dargestellt, und jeder Punkt (x, y) entspricht einer Hypersäule. Neuronen mit einer gegebenen Präferenz für die Orientierung θ (wobei θ der Winkel zwischen 0 und π ist, werden durch die Position der Hypersäule (x, y) zusammen mit dem Winkel θ angegeben - das heißt, sie werden durch drei Informationseinheiten (x, y, θ) angegeben V1-Modelle sind keine Ebene, sondern eine Ebene mit einem vollständigen Satz von Ausrichtungen für jeden Punkt.


Wenn zwei Elemente (x, y, θ) und (s, t, θ) interagieren, interagieren andere Elemente mit derselben Ausrichtung an den Punkten (x + a, y + b) und (s + a, t + b) ) und Elemente mit der Orientierung -θ an den Punkten (x, -y) und (s, -t).

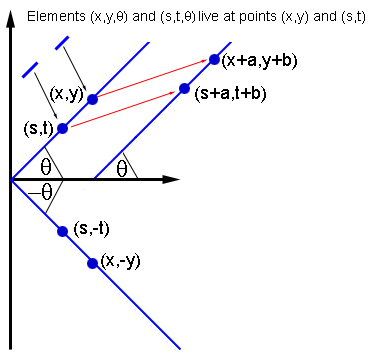
Um den anatomischen Befunden zu entsprechen, schlugen Breslov und Kollegen vor, dass das durch den Punkt (x ₀ , y ₀ , θ ₀ ) angegebene Neuron mit allen anderen Neuronen in derselben Hypersäule (x ₀ , y ₀ ) interagiert. Er interagiert jedoch nur dann mit Neuronen aus anderen Hypersäulen, wenn diese in seiner bevorzugten Ausrichtung θ _{0 liegen} : In der Ebene müssen Sie eine Linie durch den Punkt (x ₀ , y ₀ ) in einem Winkel θ _{0 ziehen} . Dann interagieren die mit dem Punkt (x ₀ , y ₀ , & thgr; ₀ ) bezeichneten Neuronen nur mit den Neuronen von Hypersäulen, die auf derselben Linie liegen, dh dieselbe bevorzugte Orientierung & thgr; _{0 haben} .

Dieses Interaktionsschema ist sehr symmetrisch. Zum Beispiel ändert es sich nicht, wenn die Ebene um irgendeine Strecke in irgendeine Richtung verschoben wird: Wenn zwei Elemente (x ₀ , y ₀ , θ ₀ ) und (s ₀ , t ₀ , φ ₀ ) interagieren, dann werden die durch die Verschiebung erhaltenen Elemente, (x ₀ + a, y ₀ + b, θ ₀ ) und (s ₀ + a, t ₀ + b, φ ₀ ) für einige a und b interagieren auf die gleiche Weise. Nach dem gleichen Prinzip ist das Schema in Bezug auf Rotationen und Reflexionen der Ebene unveränderlich.


Eine Gitterhalluzination, die durch ein mathematisches Modell erzeugt wird. Es ähnelt stark Halluzinationen, die bei der Einnahme von Marihuana auftreten.

Breslov und Kollegen verwendeten eine verallgemeinerte Version der Gleichungen aus dem ursprünglichen Modell, um die Entwicklung des Systems zu ermöglichen. Das Ergebnis ist ein Modell, das nicht nur hinsichtlich der Anatomie von V1 genauer ist, sondern auch geometrische Muster in dem Sichtfeld erzeugen kann, zu dem das ursprüngliche Modell nicht in der Lage war. Dies schließt Gittertunnel, Waben und Spinnweben ein, deren Ausrichtung die Konturen besser charakterisiert als helle und dunkle kontrastierende Bereiche.

Darüber hinaus reagiert das Modell empfindlich auf die Symmetrien von Neuroneninteraktionsschemata: Mathematiker haben gezeigt, dass diese Symmetrien die Bildung periodischer Muster nervöser Aktivität erzeugen. Das Modell geht daher davon aus, dass Halluzinationen zur Anordnung von Hypersäulen und Orientierungspräferenzen führen, dh zu Mechanismen, die uns helfen, die Gesichter, Konturen, Oberflächen und Texturen der visuellen Welt zu erkennen. Wenn diese Mechanismen beispielsweise durch die Exposition gegenüber dem Arzneimittel an Stabilität verlieren, treten Aktivitätsmuster auf, die sich in visuelle Halluzinationen verwandeln.

Jenseits von Halluzinationen

Das Breslov-Modell ermöglicht nicht nur einen Einblick in die Mechanismen, die visuelle Halluzinationen erzeugen, sondern gibt auch Hinweise auf die Architektur des Gehirns im weiteren Sinne. Zusammen mit seiner Frau, einer experimentellen Neurobiologin, untersuchte Breslov die Konturen von Hypercolumn-Verbindungen mit normalem Sehen, um zu verstehen, wie visuelle Bilder verarbeitet werden. „Die Menschen sind es gewohnt zu glauben, dass Neuronen in V1 einfach lokale Gesichter definieren und dass man zu höheren Ebenen des Gehirns gehen muss, um diese Gesichter zu sammeln und komplexere Dinge wie Konturen und Oberflächen zu erkennen. Aus unserer Arbeit mit meiner Frau geht jedoch hervor, dass diese Strukturen in V1 es dem visuellen Kortex tatsächlich ermöglichen, Konturen frühzeitig zu erkennen und eine globalere Verarbeitung durchzuführen. Es wurde angenommen, dass wir immer komplexere Aspekte des Bildes verarbeiten und in der Hierarchie des Gehirns höher steigen. Nun wurde klar, dass es eine aktive Rückkopplung zwischen dem oberen und unteren Teil des Kortex gibt."Dies ist kein einfacher hierarchischer Prozess, sondern ein unglaublich komplexes und aktives System, dessen Verständnis viele Jahre dauern wird."

Zu den praktischen Anwendungen dieser Arbeit gehört das Computer-Sehen. Informatiker bauen bereits Strukturen mit internen Verbindungen auf, mit denen Breslov und Kollegen Modelle erstellt haben, um Computern das Definieren von Konturen und Texturen beizubringen. Wenn Sie ein wenig Fantasie zeigen, können Sie sich vorstellen, dass diese Studie eines Tages dazu beitragen kann, das Sehvermögen von Menschen mit Behinderungen wiederherzustellen. „Die Frage ist, ob es möglich ist, einen Teil des visuellen Kortex unter Umgehung des Auges zu stimulieren und damit die Blinden zu orientieren“, sagt Breslov. "Wenn Sie verstehen, wie der Kortex strukturiert ist und wie er auf Stimulation reagiert, ist es vielleicht möglich, die beste Methode für die richtige Stimulation zu erfinden."

Es gibt sogar solche Anwendungsbereiche, die überhaupt nicht mit dem Gehirn verbunden sind. Breslov wandte die durch seine Arbeit gewonnenen Ideen auf andere Situationen an, in denen sich Objekte in einem Raum mit einer bestimmten Ausrichtung befinden, beispielsweise Fibroblasten aus menschlichen und tierischen Geweben. Er zeigte, dass diese interagierenden Zellen und Moleküle unter bestimmten Bedingungen sich aneinanderreihen und Muster erzeugen können, die denen in V1 ähneln.

Die Leute sprachen von Anfang an davon, Halluzinationen zu sehen, und in fast allen Kulturen - Bilder von Halluzinationen finden sich sogar in Petroglyphenund Höhlenmalereien. In den Traditionen der Schamanen auf der ganzen Welt werden sie als Botschaften aus der Welt der Geister behandelt. Nur wenige moderne Neurowissenschaftler werden der Beteiligung von Geistern zustimmen, aber als Botschafter der verborgenen Welt - diesmal der verborgenen Welt unseres Gehirns - haben diese Halluzinationen ihre Fähigkeiten nicht verloren.