Wie kann LIGO Gravitationswellen sehen, wenn sich in BRT Licht zusammen mit dem Raum erstreckt?

Wie kann LIGO Gravitationswellen erfassen, wenn sie das Licht zusammen mit dem Raum zwischen den Spiegeln strecken?

Bildnachweis : www.ligo.caltech.edu

Diese Frage stellt sich sicherlich, wenn es um die Detektion von Gravitationswellen (GW) geht. Normalerweise lautet das Argument wie folgt: Wir wissen, dass es eine Gravitationsrotverschiebung gibt , d.h. Die Schwerkraft streckt die Wellenlängen. Es ist anzunehmen, dass sich in LIGO auch das Licht ausdehnt und die Wellenlängen, die wir als „Lineal“ zur Messung des Abstands zwischen den Spiegeln verwenden, sich im gleichen Maße ausdehnen wie der Abstand selbst. Wie kann man also ein Interferometer verwenden, um Gravitationswellen zu messen?

Stellen Sie sich mögliche Antworten darauf vor:

1. GV beeinflussen das Licht nicht, daher macht die Frage keinen Sinn.
2. GWs strecken die Wellenlänge des Lichts, aber sehr schwach, so dass wir es nicht bemerken.
3. Es spielt keine Rolle, das Detektionsprinzip ist nicht wellenlängenempfindlich.
4. Detektoren funktionieren nicht wirklich.

1. Gab es einen Jungen?

Zunächst funktionieren die Detektoren noch.


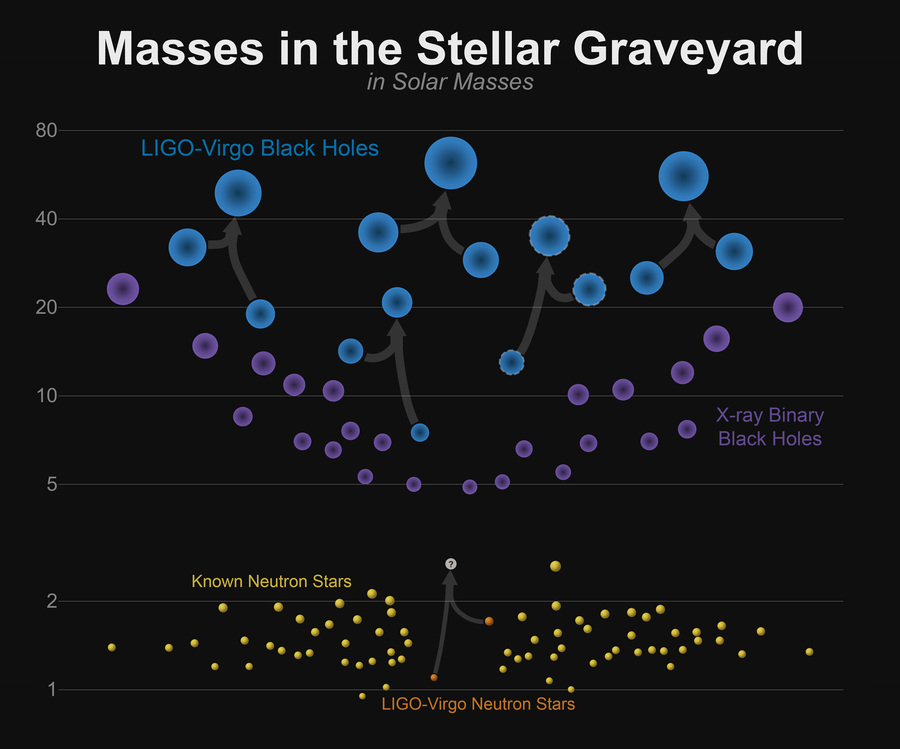Friedhof der Sterne: Massen von uns bekannten Neutronensternen und Schwarzen Löchern, einschließlich LIGO-Beobachtungen. Bildnachweis : www.ligo.caltech.edu


Im Moment haben wir mehr als ein Dutzend Ereignisse von der GW gesehen. Am überzeugendsten ist die gemeinsame Detektion von GW und Lichtblitzen aus der Fusion von Neutronensternen. In LIGO sahen sie das GW, triangulierten den Bereich am Himmel, aus dem sie stammen, und sagten zu den Teleskopen: „Schau mal!“ Sie schauten und sahen den Ausbruch des Kilons genau dort, wo es von LIGO angezeigt wurde. Es besteht also kaum ein Zweifel, dass es funktioniert. Mal sehen wie genau.

2. Was ist LIGO im Allgemeinen?

Der Virgo-Detektor ist ein europäischer Detektor, einer von drei Detektoren, die Gravitationswellen gesehen haben. Bildnachweis : www.ligo.caltech.edu

Eine Gravitationswelle, die während der Verschmelzung massereicher Objekte (z. B. zweier Schwarzer Löcher) entsteht, breitet sich in der Raumzeit als kleine Störung ihrer Krümmung aus. Dies führt dazu, dass sich die Abstände zwischen Objekten geringfügig ändern, wenn die Welle durch sie hindurchgeht (genauer gesagt, die Definition der Entfernung ändert sich). Bei LIGO ändern sich die beiden Arme eines 4 km langen Michelson-Interferometers um ~ 10 ^-18 m, und der Detektor kann diese Änderung erkennen. Ein wichtiger Punkt: Wenn der Wellenleiter einen Arm des Interferometers streckt, wird der zweite Arm proportional komprimiert (idealerweise ergibt sich dies aus der Quadrupolnatur des Wellenleiters und dem Vorhandensein von zwei Polarisationen).

Es gibt bereits einen guten Artikel über das LIGO-Gerät auf Habré. Fahren wir also mit der Antwort auf die am Anfang des Artikels gestellte Frage fort.

3. Messkonzept

Eine Animation, die zeigt, wie der Detektor funktioniert

Betrachten Sie zunächst ein Beispiel, das Ihnen hilft, das Grundprinzip des Detektors zu verstehen.
Dieser Detektor arbeitet mit kontinuierlichem Licht - der Laser pumpt die Resonatoren in LIGO ständig mit Licht und Fotodioden erkennen ständig das Vorhandensein / Fehlen eines Signals. Vereinfachen wir zum Beispiel das Schema: Nehmen wir an, wir haben eine Photonenquelle, die gleichzeitig Photonen in zwei Richtungen sendet, wo sie von den Spiegeln reflektiert und zum Photonendetektor (in unserem Fall zum Strahlteiler) zurückgeführt werden, wie in der folgenden Abbildung gezeigt.



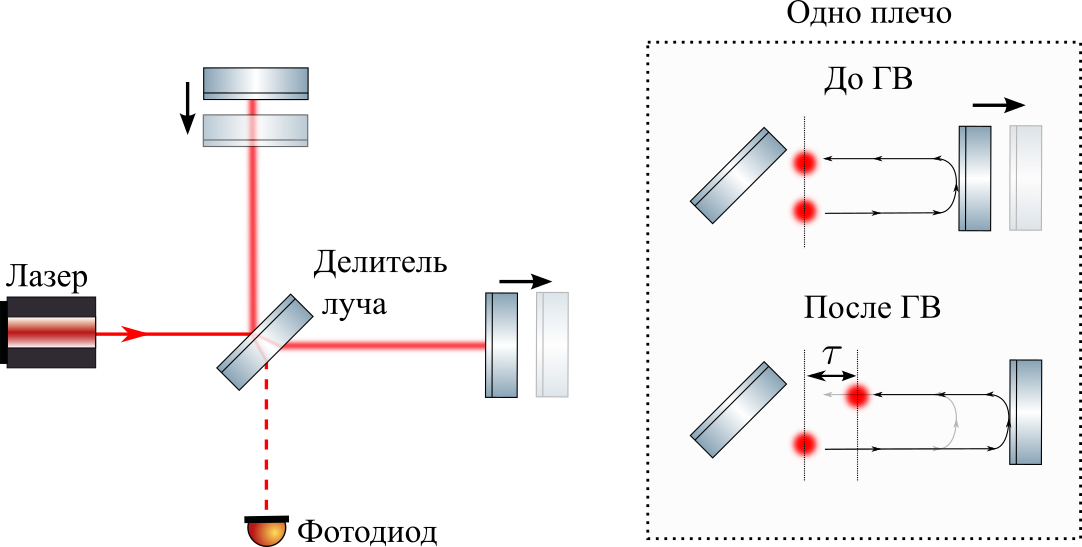
Wenn sich zwei Spiegel in gleichem Abstand von der Photonenquelle befinden, kehren zwei Photonen gleichzeitig zum Detektor zurück (wie in der obigen Abbildung). Wenn GW eine Schulter streckt $$$x$ und komprimiert einen anderen auf $$$x$ dann kommt ein Photon früher als ein anderes $$$2 \ tau = 4x / c \ sim 4 \ mal 10 ^ {- 18} / (3 * 10 ^ 8) \ sim 10 ^ {- 26}$ c, wie in der obigen Abbildung. Das ist natürlich sehr klein und es wäre unmöglich, direkt zu messen, aber wir messen ein wenig anders. Ich wollte nur die Hauptbotschaft dieses Beitrags demonstrieren:

Der Detektor ist kein Lineal, sondern eine Uhr

4. Detaillierte Erklärung

Betrachten wir nun das Michelson-Interferometer, in das sie mit einem kontinuierlichen Laser leuchten. Der Strahl wird gleichmäßig auf dem Strahlteiler aufgeteilt, von den endgültigen Spiegeln reflektiert und stört, wenn er zum Strahlteiler zurückkehrt.



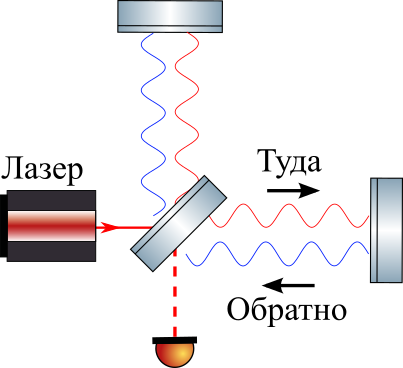
Der Einfachheit halber nehmen wir an, dass das GW ein "Schritt" ist - es ändert die Metrik sofort um einen kleinen Betrag $$$h_0$ . Mit den Worten "metrische Änderung" meinen wir, dass sich die Definition der Entfernung etwas ändert, d.h. Alle Entfernungen nehmen zu (oder ab) $$$(1+ h_0 / 2)$ mal. Wenn wir den Abstand zwischen dem Strahlteiler und dem endgültigen Spiegel berücksichtigen $$$L$ Wenn sich die Metrik ändert, erhöht sie sich um $$$\ Delta L$ so dass $$$h_0 = 2 \ Delta L / L$ .

Hinweis: Es ist wichtig, dass die Darstellung des GW als „Schritt“ nur zur Betrachtung an den Fingern nützlich ist. In der Realität ist es erforderlich, das GW als Welle mit einer bestimmten Länge zu betrachten.

Überlegen Sie, was in diesem Moment mit Licht passiert.


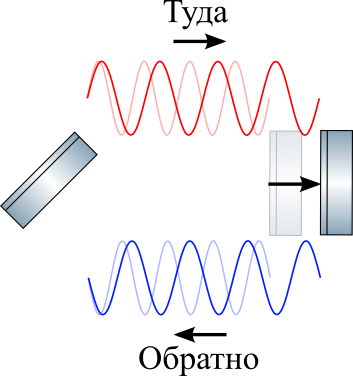Zum Zeitpunkt des Eintreffens des GW wird die Wellenlänge des Lichts relativ zur ursprünglichen Wellenlänge (durchscheinende Kurven) gestreckt. NB: Die gezeigte Wellenlänge ist aus Gründen der Klarheit mit der Schulterlänge vergleichbar. Tatsächlich beträgt die Laserwellenlänge etwa 1 Mikron und die Schulterlänge 4 km.

Wenn der Spiegel vor dem Dehnen einen Knoten einer stehenden Welle hatte, bleibt er nach dem Dehnen dort, wie im obigen Bild gezeigt. Warum? Dies wird von der Relativitätstheorie verlangt: Da es kein separates unabhängiges Ruhesystem gibt, hat der Knoten nichts zu tun, als dort zu bleiben, wo er relativ zur Oberfläche des Spiegels war. Das heißt, die Wellenlänge nimmt zu $$$(1 + h_0 / 2)$ Zeiten, wie zu Beginn des Artikels erwartet, in Analogie zur Gravitationsrotverschiebung.

Es stellt sich also heraus, dass das Licht trotzdem zusammen mit dem Detektor gestreckt wurde und wir das Signal nicht registrieren können?

Und doch können wir!



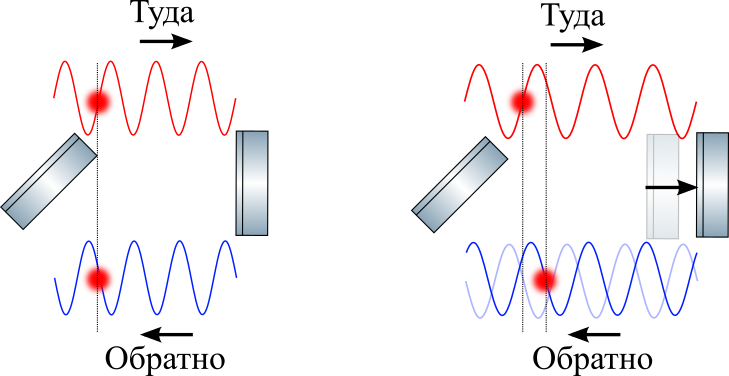
Wir werden dies im obigen Bild zeigen: Wir werden den Pfad eines bestimmten Knotens in einer gestreckten Welle auf dem Weg hin und zurück verfolgen und ihn mit einem Kreis markieren. Trotz der Dehnung breitet sich das Licht immer noch mit Lichtgeschwindigkeit aus. Dies bedeutet, dass für den Teil der Welle, der gerade in die Schulter eingetreten ist, mehr Zeit benötigt wird, um die Rundreise zu überwinden (siehe hier Absatz 3 aus dem Artikel). Das heißt, seine Phase bei der Ankunft ändert sich (wie auf dem Bild zu sehen ist).

Darüber hinaus pumpt Licht weiterhin Licht mit einer ungedehnten Wellenlänge.

Die vom Licht auf dem Weg vom Teiler zum Spiegel und umgekehrt akkumulierte Phase hängt von der Eigenfrequenz des Lichts ab $$$\ omega _ {\ rm schluchz}$ auf dem Strahlteiler und Zeit beobachtet $$$\ tau _ {\ rm Hin- und Rückfahrt}$ ::

$$

$$\ phi = \ omega _ {\ rm schluchz} \ tau _ {\ rm Hin- und Rückfahrt}$$

Es kann gezeigt werden (zum Beispiel hier oder hier ), dass sich die Eigenfrequenz praktisch nicht ändert, wenn die Wellenlänge des HW viel größer als die Länge des Arms des Interferometers ist. Die Verzögerungszeit hängt vom Abstand zwischen den Spiegeln ab:

$$

$$\ tau _ {\ rm Hin- und Rückfahrt} \ approx \ frac {2 L} {c} (1+ \ frac {h_0} {2})$$

Dementsprechend wird die Lichtphase beim Eintreffen des Strahlteilers abhängig von der Größe der Metrik eine Verzögerung aufweisen $$$h_0$ . Auf der anderen Schulter passiert alles gleich, genau auf das Schild vor $$$h_0$ - weil diese Schulter nicht gedehnt, sondern zusammengedrückt wird. Infolgedessen beträgt auf dem Strahlteiler die Phasendifferenz zwischen den beiden Schultern

$$

$$\ Delta \ phi = \ frac {2 \ omega L} {c} (1+ \ frac {h_0} {2}) - \ frac {2 \ omega L} {c} (1- \ frac {h_0} { 2}) = 2 \ pi \ frac {L} {\ lambda} h_0$$

Aus dieser Gleichung ist übrigens ersichtlich, warum der Detektor einen so langen Arm hat - je länger die Länge L im Vergleich zur Wellenlänge ist, desto empfindlicher ist der Detektor. Detektoren der nächsten Generation wie das Einstein-Teleskop oder der Cosmic Explorer werden noch länger sein - von 10 bis 40 km.

Ich stelle fest, dass das GW in Wirklichkeit kein „Schritt“ ist, sondern eine Welle mit einer Wellenlänge, die viel länger als die Schulterlänge ist. Während des Streckens geht also ein „Knoten“ der Lichtwelle hin und her, dessen Dehnung vernachlässigt werden kann. Daher fehlt der erste Moment des "Streckens" des Lichts aus der Betrachtung "an den Fingern" tatsächlich praktisch.

Also die Schlussfolgerung. Die richtige Antwort auf die Frage steht am Anfang des Artikels: Sowohl 2 als auch 3 - Gravitationswellen wirken auf Licht etwas anders als auf den Abstand zwischen den Spiegeln, aber das spielt keine Rolle, da wir auf jeden Fall nicht die Wellenlänge, sondern die Phasenverzögerung messen. Mit anderen Worten

Der Gravitationswellendetektor funktioniert wie eine Uhr, nicht wie ein Lineal.

5. Fazit

Es ist wichtig zu betonen, dass die Gravitationswelle die Wellenlänge des Lichts anders beeinflusst als den Abstand zwischen den Spiegeln. Dies ist hauptsächlich auf die Tatsache zurückzuführen, dass die Periode des GW viel länger ist als die Zeit, die das Licht benötigt, um hin und her zu gehen. Der Arm des Interferometers dehnt sich nach der Zeit des GW im Laufe der Zeit weiter aus, und das Licht kommt ständig "neu" vom Laser.

Darüber hinaus verfügt der reale Detektor über zusätzliche Spiegel, die mehrere Resonatoren erzeugen, wodurch die Länge der Schulter effektiv erhöht wird. Dies hat jedoch keinen Einfluss auf die Hauptidee.

Wir können also wirklich Gravitationswellen beobachten und keine Verschwörungstheorien!

Bildnachweis : www.ligo.caltech.edu

6. LIGO News

Als Postskriptum ein wenig darüber, was jetzt in LIGO passiert. Der zweite Beobachtungszyklus von O2 brachte nicht nur die Beobachtung der Fusion von Neutronensternen und die erste gemeinsame Beobachtung von HS durch drei Detektoren , einschließlich Virgo, sondern auch viele andere Ereignisse. In naher Zukunft werden die Ergebnisse der Datenanalyse veröffentlicht und die Daten selbst werden offen und für die Analyse verfügbar sein.

LIGO führt jetzt zahlreiche Aktualisierungen durch, einschließlich der Installation von komprimiertem Licht und eines leistungsstärkeren Lasers, wodurch die Empfindlichkeit des Detektors um ein Vielfaches erhöht wird und Sie viel mehr Ereignisse beobachten können (in einem guten Szenario - nach Ereignis pro Woche).

Anfang nächsten Jahres wird ein neuer O3-Beobachtungszyklus beginnen.