Laplace-Unschärfe - Ist es möglich, Laplace anstelle von Gauß zu blubbern, wie oft ist es schneller und ist es den Verlust von 1/32 Genauigkeit wert?

"Unschärfe" bei gewöhnlichen Menschen ist ein Unschärfeeffekt in der digitalen Bildverarbeitung. Es kann an sich und als Bestandteil von Schnittstellenanimationen oder komplexeren abgeleiteten Effekten (Bloom / FocusBlur / MotionBlur) sehr effektiv sein. Bei alledem ist ehrlicher Blues in der Stirn eher langsam. Und oft lassen die in die Zielplattform integrierten Implementierungen zu wünschen übrig. Entweder ist die Geschwindigkeit traurig, die Artefakte verletzen die Augen. Die Situation führt zu vielen Kompromissimplementierungen, die für bestimmte Bedingungen besser oder schlechter geeignet sind. Eine originelle Implementierung mit guter Zuverlässigkeitsqualität und höchster Geschwindigkeit, während die geringste Abhängigkeit von Hardware unter dem Strich auf Sie wartet. Guten Appetit!

(Laplace Blur - Vorgeschlagener ursprünglicher Algorithmusname)

Heute hat mich meine interne Demoszene getreten und mich gezwungen, einen Artikel zu schreiben, der vor sechs Monaten geschrieben werden musste. Als Amateur möchte ich der Öffentlichkeit in aller Ruhe einen „fast gausischen Blurah“ -Algorithmus anbieten, der durch die Verwendung außergewöhnlich schneller Prozessoranweisungen (Verschiebungen und Masken) gekennzeichnet ist und daher für die Implementierung bis zu Mikrocontrollern zugänglich ist (extrem schnell in einer begrenzten Umgebung).

Gemäß meiner Tradition, Artikel über Habr zu schreiben, werde ich Beispiele in JS als beliebteste Sprache nennen und ob Sie es glauben oder nicht, es ist sehr praktisch für den Zweck des Rapid Prototyping von Algorithmen. Darüber hinaus war die Möglichkeit, dies effektiv in JS zu implementieren, mit typisierten Arrays verbunden. Auf meinem nicht sehr leistungsstarken Laptop wird das Vollbild mit einer Geschwindigkeit von 30 fps verarbeitet (Multithreading von Arbeitern war nicht beteiligt).


Diese Beschreibung ist hier eher vorhanden, um den Verlauf meiner Gedanken und Vermutungen zu erklären, die mich zum Ergebnis geführt haben. Für diejenigen, die interessiert sein werden:

Ursprüngliche Gauß-Funktion:



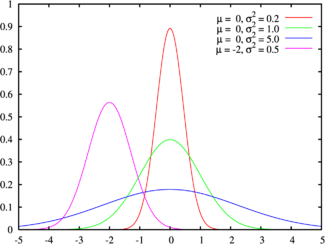
g (x) = a * e ** (- ((xb) ** 2) / c), wobei
a ist die Amplitude (wenn wir acht Farbbits pro Kanal haben, dann ist es = 256)
e ist die Eulerkonstante ~ 2.7
b - Graphverschiebung in x (wir brauchen nicht = 0)
c - Parameter, der die Breite des damit verbundenen Diagramms beeinflusst, als ~ w / 2.35

Unsere private Funktion (minus vom Exponenten, der durch Ersetzen der Multiplikation durch Division entfernt wurde):



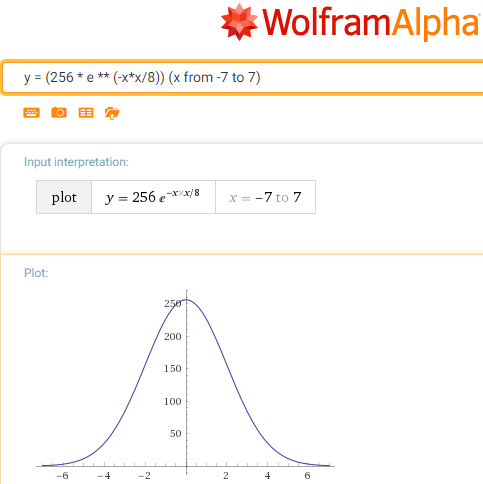
g (x) = 256 / e ** (x * x / c)

Lassen Sie die schmutzige Approximationsaktion beginnen:
Beachten Sie, dass Parameter c sehr nahe an der halben Breite liegt und 8 eingestellt ist (dies liegt daran, wie viele Schritte Sie jeweils um einen 8-Bit-Kanal verschieben können).

Wir ersetzen e auch grob durch 2, wobei wir jedoch feststellen, dass dies die Krümmung der „Glocke“ stärker beeinflusst als ihre Grenzen. Eigentlich betrifft es 2 / e-mal, aber die Überraschung ist, dass dieser Fehler den Parameter c kompensiert, so dass die Randbedingungen noch in Ordnung sind und der Fehler nur in einer leicht falschen „Normalverteilung“ für die Grafik erscheint Algorithmen, dies wird die Dynamik von Farbverläufen mit Farbverläufen beeinflussen, aber es ist fast unmöglich, mit dem Auge zu bemerken.

Unsere Funktion lautet nun wie folgt:
gg (x) = 256/2 ** (x * x / 8) oder gg (x) = 2 ** (8 - x * x / 8)
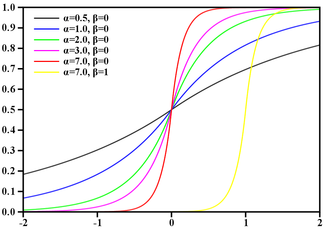
Es ist zu beachten, dass der Exponent (x * x / 8) den gleichen Wertebereich [0-8] wie die Funktion eines Abs (x) niedrigerer Ordnung hat, daher ist letzterer ein Kandidat für eine Ersetzung. Wir werden die Vermutung schnell überprüfen, indem wir uns ansehen, wie sich der Graph damit ändert. Gg (x) = 256 / (2 ** abs (x)):

GaussBlur gegen LaplasBlur:



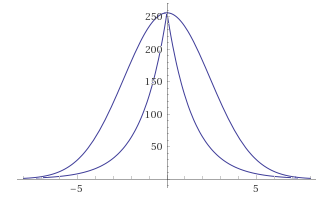
Abweichungen scheinen zu groß zu sein, außerdem hat die Funktion, die ihre Glätte verloren hat, jetzt einen Höhepunkt. Aber hey.

Vergessen wir zunächst nicht, dass die Glätte der durch Unschärfe erhaltenen Gradienten nicht von der Wahrscheinlichkeitsdichtefunktion (der Gauß-Funktion) abhängt, sondern von ihrem Integral - der Verteilungsfunktion. Zu dieser Zeit kannte ich diese Tatsache nicht, aber nachdem ich eine „destruktive“ Näherung in Bezug auf die Wahrscheinlichkeitsdichtefunktion (Gauß) durchgeführt hatte, blieb die Verteilungsfunktion ziemlich ähnlich.

Es war:



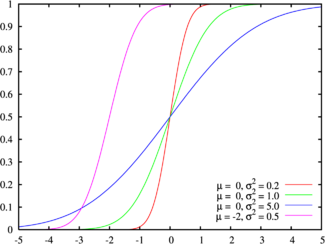
Es wurde:



Der Beweis, der dem vorgefertigten Algorithmus entnommen wurde, stimmt überein:



(Mit Blick auf die Zukunft werde ich sagen, dass der Unschärfefehler meines Algorithmus in Bezug auf Gausian x5 nur 3% betrug.)

Wir sind also der Laplace-Verteilungsfunktion viel näher gekommen. Wer hätte das gedacht, aber sie können die Bilder zu 97% nicht schlechter waschen.

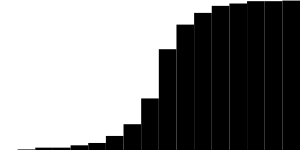
Beweis, Unterschiede Gausian Blura x5 und "Laplace Blura" x7:



(Dies ist kein schwarzes Bild! Sie können im Editor studieren)

Die Annahme dieser Transformation ermöglichte es uns, zu der Idee überzugehen, den Wert durch iterative Filterung zu erhalten, auf die ich zunächst reduzieren wollte.

Bevor ich einen bestimmten Algorithmus erzähle, ist es ehrlich, wenn ich vorauslaufe und sofort seinen einzigen Nachteil beschreibe (obwohl die Implementierung mit einem Geschwindigkeitsverlust behoben werden kann). Dieser Algorithmus wird jedoch unter Verwendung von Scherarithmetik implementiert, und Potenzen von 2 sind seine Begrenzung. Das Original verwischt also x7 (was in Tests am ehesten mit Gausian x5 zusammenhängt). Diese Implementierungsbeschränkung ist auf die Tatsache zurückzuführen, dass bei einer 8-Bit-Farbe, bei der der Wert im Filterantrieb um ein Bit pro Schritt verschoben wird, jede Aktion vom Punkt aus in maximal 8 Schritten endet. Ich habe auch eine etwas langsamere Version durch Proportionen und zusätzliche Ergänzungen implementiert, die eine schnelle Division durch 1,5 implementiert (was zu einem Radius von x15 führt). Mit der weiteren Anwendung dieses Ansatzes steigt jedoch der Fehler und die Geschwindigkeit sinkt, was eine solche Verwendung nicht zulässt. Andererseits ist anzumerken, dass x15 bereits ausreicht, um den Unterschied nicht zu bemerken. Das Ergebnis wird aus dem Original oder aus dem heruntergetasteten Bild erhalten. Die Methode eignet sich daher gut, wenn Sie in einer begrenzten Umgebung eine außergewöhnliche Geschwindigkeit benötigen.

Der Kern des Algorithmus ist also einfach: Es werden vier Durchgänge desselben Typs ausgeführt:

1. Die Hälfte des Wertes des Laufwerks t (anfänglich gleich Null) wird zur Hälfte des Wertes des nächsten Pixels addiert, das Ergebnis wird ihm zugewiesen. Fahren Sie auf diese Weise bis zum Ende der Bildzeile fort. Für alle Zeilen.

Nach Abschluss des ersten Durchgangs wird das Bild in eine Richtung unscharf.

2. Beim zweiten Durchgang machen wir für alle Linien dasselbe in die entgegengesetzte Richtung.
Wir erhalten ein Bild, das horizontal vollständig unscharf ist.

3-4. Machen Sie jetzt dasselbe vertikal.
Fertig!

Anfangs habe ich einen Zwei-Pass-Algorithmus mit der Implementierung von Back-Blur durch den Stack verwendet, aber es ist schwer zu verstehen, nicht anmutig, und es stellte sich heraus, dass es auf aktuellen Architekturen langsamer ist. Möglicherweise ist der One-Pass-Algorithmus auf Mikrocontrollern schneller, und die Möglichkeit, das Ergebnis schrittweise auszugeben, ist ebenfalls von Vorteil.

Bei der aktuellen Vier-Wege-Implementierungsmethode habe ich mir Habré vom vorherigen Guru über Unschärfealgorithmen angesehen. habr.com/post/151157 Ich nutze diese Gelegenheit, um ihm meine Solidarität und tiefe Dankbarkeit auszudrücken.

Aber die Hacks endeten nicht dort. Nun erfahren Sie, wie Sie alle drei Farbkanäle in einer Prozessoranweisung berechnen! Tatsache ist, dass Sie mit der Bitverschiebung, die als Division durch zwei verwendet wird, die Position der Ergebnisbits sehr gut steuern können. Das einzige Problem besteht darin, dass die unteren Bits der Kanäle in benachbarte höhere Bits verschoben werden. Sie können sie jedoch einfach zurücksetzen, um das Problem mit einem gewissen Genauigkeitsverlust zu beheben. Und gemäß der beschriebenen Filterformel führt die Addition des halben Wertes des Laufwerks mit dem halben Wert der nächsten Zelle (vorbehaltlich des Zurücksetzens der entladenen Bits) niemals zu einem Überlauf, sodass Sie sich darüber keine Sorgen machen sollten. Und die Filterformel für die gleichzeitige Berechnung aller Ziffern lautet wie folgt:

buf32 [i] = t = (((t >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);

Es ist jedoch noch eine weitere Ergänzung erforderlich: Es wurde experimentell festgestellt, dass der Genauigkeitsverlust in dieser Formel zu signifikant ist und die Helligkeit des Bildes visuell signifikant springt. Es wurde klar, dass das verlorene Bit auf das nächste Ganze gerundet und nicht verworfen werden muss. Eine einfache Möglichkeit, dies in Ganzzahlarithmetik zu tun, besteht darin, die Hälfte des Divisors vor der Division zu addieren. Unser Divisor ist zwei, daher müssen Sie in allen Ziffern eine hinzufügen - die Konstante 0x010101. Aber bei jedem Zusatz muss man vorsichtig sein, wenn es zu einem Überlauf kommt. Daher können wir eine solche Korrektur nicht verwenden, um den halben Wert der nächsten Zelle zu berechnen. (Wenn es weiße Farbe gibt, werden wir überlaufen, daher werden wir es nicht korrigieren). Es stellte sich jedoch heraus, dass der Hauptfehler in der mehrfachen Aufteilung des Laufwerks lag, die wir nur korrigieren können. Denn selbst bei einer solchen Korrektur steigt der Wert im Antrieb nicht über 254. Bei Addition zu 0x010101 kann jedoch kein Überlauf garantiert werden. Und die Filterformel mit Korrektur hat folgende Form:

buf32 [i] = t = (((((0x010101 + t) >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);

Tatsächlich führt die Formel die Korrektur recht gut durch. Wenn Sie diesen Algorithmus wiederholt auf das Bild anwenden, werden Artefakte erst in den zweiten zehn Durchgängen sichtbar. (nicht die Tatsache, dass das Wiederholen der Gausianischen Blura solche Artefakte nicht hervorbringt).

Darüber hinaus gibt es ein wunderbares Anwesen mit vielen Pässen. (Dies liegt nicht an meinem Algorithmus, sondern an der "Normalität" der Normalverteilung). Bereits beim zweiten Durchgang der Laplace Blura sieht die Wahrscheinlichkeitsdichtefunktion (wenn ich alles richtig gemacht habe) ungefähr so ​​aus:



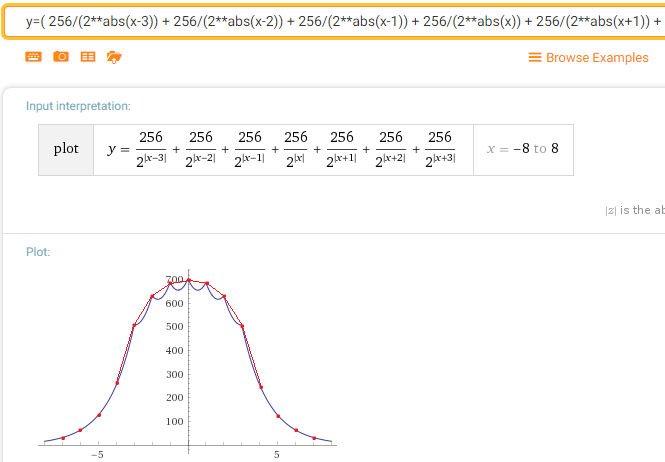
Was, wie Sie sehen, dem Gaußschen schon sehr nahe kommt.

Empirisch fand ich, dass die Verwendung von Modifikationen mit einem großen Radius paarweise zulässig ist, weil Die oben beschriebene Eigenschaft kompensiert Fehler, wenn der letzte Durchgang genauer ist (der genaueste ist der hier beschriebene x7-Unschärfealgorithmus).

Demo
Rap
codpen

Ein Appell an coole Mathematiker:
Was interessant wäre zu wissen, wie richtig es ist, einen solchen Filter getrennt zu verwenden, ich bin mir nicht sicher, ob es ein symmetrisches Verteilungsbild gibt. Obwohl die Heterogenität des Auges nicht sichtbar ist.

upd: Hier werde ich nützliche Links ansprechen, die freundlicherweise von Kommentatoren präsentiert und von anderen Khabroviten gefunden wurden.
1. Wie Intel-Assistenten basierend auf der Leistung von SSE funktionieren - software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (danke vladimirovich )
2. Theoretische Grundlage zum Thema „Schnelle Bildfaltungen“ + einige seiner benutzerdefinierten Anwendungen in Bezug auf ehrliche Gaußsche Blau - blog.ivank.net/fastest-gaussian-blur.html (danke Grox )

Vorschläge, Kommentare, konstruktive Kritik sind willkommen!