Numerische Überprüfung der abc-Hypothese (ja, diese)

Hallo Habr.

Es gab bereits mehrere Artikel zur abc-Hypothese im Geektimes Habr (zum Beispiel 2013 und 2018 ). Die Geschichte selbst über einen Satz, der zunächst über viele Jahre nicht bewiesen und dann nicht über die gleiche Anzahl von Jahren verifiziert werden kann, verdient zumindest einen Spielfilm. Aber im Schatten dieser wunderbaren Geschichte wird der Satz selbst als zu oberflächlich angesehen, obwohl er nicht weniger interessant ist. Schon die Tatsache, dass die ABC-Hypothese eines der wenigen ungelösten Probleme der modernen Wissenschaft ist, deren Aussage selbst ein Fünftklässler verstehen kann. Wenn diese Hypothese wirklich wahr ist, folgt sie leicht aus dem Beweis anderer wichtiger Sätze, zum Beispiel dem Beweis des Satzes von Fermat .

Ohne Motizuki-Lorbeeren zu beanspruchen, habe ich mich auch entschlossen, mit einem Computer zu überprüfen, inwieweit die in der Hypothese versprochene Gleichheit erfüllt ist. Warum nicht - moderne Prozessoren sind nicht nur zum Spielen gedacht - warum nicht einen Computer für seinen Haupt- (Rechen-) Zweck verwenden ...

Wen interessiert es, was passiert ist, bitte unter der Katze.

Erklärung des Problems

Beginnen wir von vorne. Worum geht es im Satz? Wie Wikipedia sagt (der Wortlaut in der englischen Version ist etwas klarer), gibt es für gegenseitig Primzahlen (ohne gemeinsame Teiler) die Zahlen a, b und c, so dass a + b = c, für jedes ε> 0 eine begrenzte Anzahl von Tripeln a + b = c, so dass:



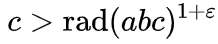
Die rad-Funktion wird als Radikal bezeichnet und bezeichnet das Produkt von Primfaktoren einer Zahl. Zum Beispiel ist rad (16) = rad (2 · 2 · 2 · 2) = 2, rad (17) = 17 (17 ist eine Primzahl), rad (18) = rad (2 · 3 · 3) = 2 · 3 = 6, rad (1.000.000) = rad (2 ^ 6 ≤ 5 ^ 6) = 2 · 5 = 10.

Tatsächlich besteht das Wesen des Satzes darin, dass die Anzahl solcher Tripel ziemlich gering ist. Wenn wir zum Beispiel zufällig ε = 0,2 und die Gleichheit 100 + 27 = 127 nehmen: rad (100) = rad (2 · 2 · 5 · 5) = 10, rad (27) = rad (3 · 3 · 3) = 3, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (c) = 3810, 3810 ^ 1,2 ist deutlich größer als 127, die Ungleichung gilt nicht. Es gibt jedoch Ausnahmen, zum Beispiel für die Gleichheit 49 + 576 = 625, die Bedingung des Satzes ist erfüllt (diejenigen, die dies wünschen, können dies selbst überprüfen).

Der nächste Schlüsselmoment für uns ist nach dem Theorem eine begrenzte Anzahl dieser Gleichungen. Das heißt, Dies bedeutet, dass Sie einfach versuchen können, alle auf einem Computer zu sortieren. Dies gibt uns den Nobelpreis eine ziemlich interessante Programmieraufgabe.

Also fangen wir an.

Quellcode

Die erste Version wurde in Python geschrieben, und obwohl diese Sprache für solche Berechnungen zu langsam ist, ist das Schreiben von Code einfach und unkompliziert, was für das Prototyping praktisch ist.

Radikalisierung : Wir zerlegen die Zahl in Primfaktoren, entfernen dann die Wiederholungen und konvertieren das Array in eine Menge. Dann holen Sie sich einfach das Produkt aller Elemente.

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result 

Gegenseitige Primzahlen : Faktorisieren Sie die Zahlen und überprüfen Sie einfach den Schnittpunkt der Mengen.

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0 

Check : Wir verwenden bereits erstellte Funktionen, hier ist alles einfach.

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625) 

Wer möchte, kann unabhängig experimentieren, indem er den obigen Code in einen beliebigen Online-Python-Spracheditor kopiert. Natürlich läuft der Code wie erwartet wie erwartet, und es wäre zu lang, alle Tripel auf mindestens eine Million aufzulisten. Unterhalb des Spoilers befindet sich eine optimierte Version, deren Verwendung empfohlen wird.

Die endgültige Version wurde in C ++ mit Multithreading und einigen Optimierungen neu geschrieben (das Arbeiten in C mit sich überschneidenden Mengen wäre zu hardcore, wenn auch wahrscheinlich schneller). Der Quellcode befindet sich unter dem Spoiler, er kann im kostenlosen g ++ - Compiler kompiliert werden, der Code funktioniert unter Windows, OSX und sogar auf dem Raspberry Pi.


Für diejenigen, die zu faul sind, um den C ++ - Compiler zu installieren, wird eine leicht optimierte Python-Version bereitgestellt, die in jedem Online-Editor gestartet werden kann (ich habe https://repl.it/languages/python verwendet ).

Ergebnisse

Die Tripel a, b, c sind wirklich sehr wenige.

Einige Ergebnisse sind unten angegeben:
N = 10 : 1 "drei", Vorlaufzeit <0,001c
1 + 8 = 9

N = 100 : 2 "Tripel", Laufzeit <0,001c
1 + 8 = 9
1 + 80 = 81

N = 1000 : 8 "Tripel", Laufzeit <0,01 c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625

N = 10000 : 23 "Tripel", Laufzeit 2s


N = 100000 : 53 Tripel, Laufzeit 50c


Mit N = 1.000.000 haben wir nur 102 "Tripel", eine vollständige Liste finden Sie unter dem Spoiler.


Leider arbeitet das Programm immer noch langsam, ich habe nicht auf Ergebnisse für N = 10.000.000 gewartet, die Berechnungszeit beträgt mehr als eine Stunde (vielleicht habe ich irgendwo einen Fehler bei der Optimierung des Algorithmus gemacht und kann es besser machen).

Noch interessanter ist es, die Ergebnisse grafisch zu sehen:



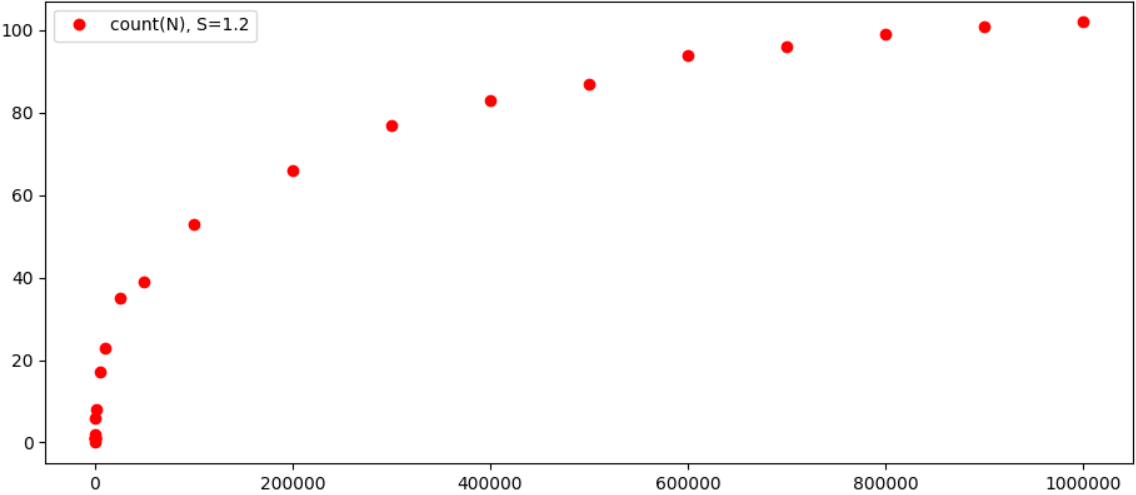
Im Prinzip ist es ziemlich offensichtlich, dass die Abhängigkeit der Anzahl möglicher Tripel von N merklich langsamer wächst als N selbst, und es ist wahrscheinlich, dass das Ergebnis für jedes ε zu einer bestimmten Zahl konvergiert. Übrigens nimmt mit einer Zunahme von ε die Anzahl der Tripel merklich ab, zum Beispiel haben wir für ε = 0,4 nur 2 Gleichheiten für N <100000 (1 + 4374 = 4375 und 343 + 59049 = 59392). Im Allgemeinen scheint das Theorem also wirklich zu gelten (nun, und wahrscheinlich wurde es bereits auf leistungsfähigeren Computern getestet, und vielleicht wurde dies alles schon lange berechnet).

Diejenigen, die dies wünschen, können selbst experimentieren. Wenn jemand Ergebnisse für Zahlen von 10.000.000 und höher hat, füge ich sie gerne dem Artikel hinzu. Natürlich wäre es interessant, bis zu dem Moment zu „zählen“, an dem die Menge der „Tripel“ nicht mehr wächst, aber es kann sehr lange dauern, die Berechnungsgeschwindigkeit scheint von N als N * N (oder vielleicht N ^ 3) und dem Prozess abzuhängen sehr lang. Trotzdem ist eine erstaunliche Sache in der Nähe, und diejenigen, die es wünschen, können sich der Suche anschließen.

Bearbeiten: Wie in den Kommentaren vorgeschlagen, hat Wikipedia bereits eine Tabelle mit den Ergebnissen - im Bereich N bis 10 ^ 18 wächst die Anzahl der "Tripel" immer noch, so dass das "Ende" des Satzes noch nicht gefunden wurde. Umso interessanter - die Intrige bleibt erhalten.