Ein Beugungsmuster findet sich in der Verteilung von Primzahlen, ähnlich der von Quasikristallen

Im März 2016 eröffneten Robert J. Lemke-Oliver und Kannan Sundararajan von der Stanford University ein neues Muster für die Verteilung von Primzahlen. Es stellte sich heraus, dass Primzahlen spezifisch über den Zahlenraum verteilt sind. Weitere Einzelheiten finden Sie in der Übersetzung des Artikels „Struktur und Zufälligkeit von Primzahlen“ über Habré.

Experten aus anderen Bereichen, einschließlich der Chemie, nahmen an der Untersuchung des Themas teil. Und erfolgreich. Der Professor für Theoretische Chemie Salvatore Torcuato fand zusammen mit dem Zahlentheoretiker Matthew de Courcy-Ireland neue Muster in der Verteilung von Primzahlen, die bisher nicht bekannt waren. Es stellte sich heraus, dass die Verteilung der Primzahlen ein fraktales Beugungsmuster bildet, das dem Beugungsmuster exotischer Quasikristalle etwas ähnlich ist.

Professor Torcuato ist spezialisiert auf die Untersuchung von Mustern in den Strukturen physikalischer Systeme wie Kristalle und Kolloide. Die Standardmethode zur Untersuchung der Struktur ist die Röntgenbeugung. Zufällige Moleküle in Flüssigkeiten oder Gasen reflektieren Strahlen in alle Richtungen, ohne ein wahrnehmbares Muster zu erzeugen. Symmetrisch angeordnete Atome in einem Kristall reflektieren jedoch synchron Lichtwellen und erzeugen periodisch helle Flecken mit ausgeprägter Beugung ( Bragg-Peaks ). Eine Analyse der Bragg-Peaks ermöglicht es, die innere Struktur eines Kristalls oder eines anderen Materials zu verstehen, das ein solches Bild erzeugt.

In neuen wissenschaftlichen Artikeln von Torkuato und anderen ( 1 , 2 , 3 ) wird gezeigt, dass die entdeckte geordnete Struktur bei der Verteilung von Primzahlen nichts anderes als ein fraktalartiges Beugungsmuster ist, ähnlich dem von Quasikristallen.

Das Bild von Bragg-Peaks auf einem Gitter von Primzahlen ähnelt Quasikristallen, unterscheidet sich jedoch immer noch von diesen. Torcuato sagt, dass Primzahlen als physikalisches System "eine völlig neue Kategorie von Strukturen sind". Forscher haben dieses neue fraktale Muster als "effektive Grenzperiodizität" bezeichnet.

Die Figur besteht aus einer periodischen Folge von hellen Spitzen, die die häufigsten Primzahlintervalle widerspiegeln: Sie sind alle ungerade (außer 2), viele nebeneinander. Die hellsten Peaks (durch zwei Ziffern getrennte Paare) wechseln sich in regelmäßigen Abständen mit weniger hellen Peaks ab, die durch sechs Ziffern getrennte Primzahlen widerspiegeln. Zwischen ihnen befinden sich noch schwächere Peaks, die weiter entfernten Primzahlenpaaren usw. entsprechen. All dies ist eine unendliche Anzahl von Bragg-Peaks, die ineinander angeordnet sind.


Eine ähnliche Struktur der Bragg-Peaks wurde früher beobachtet - in den Beugungsmustern von Quasikristallen.


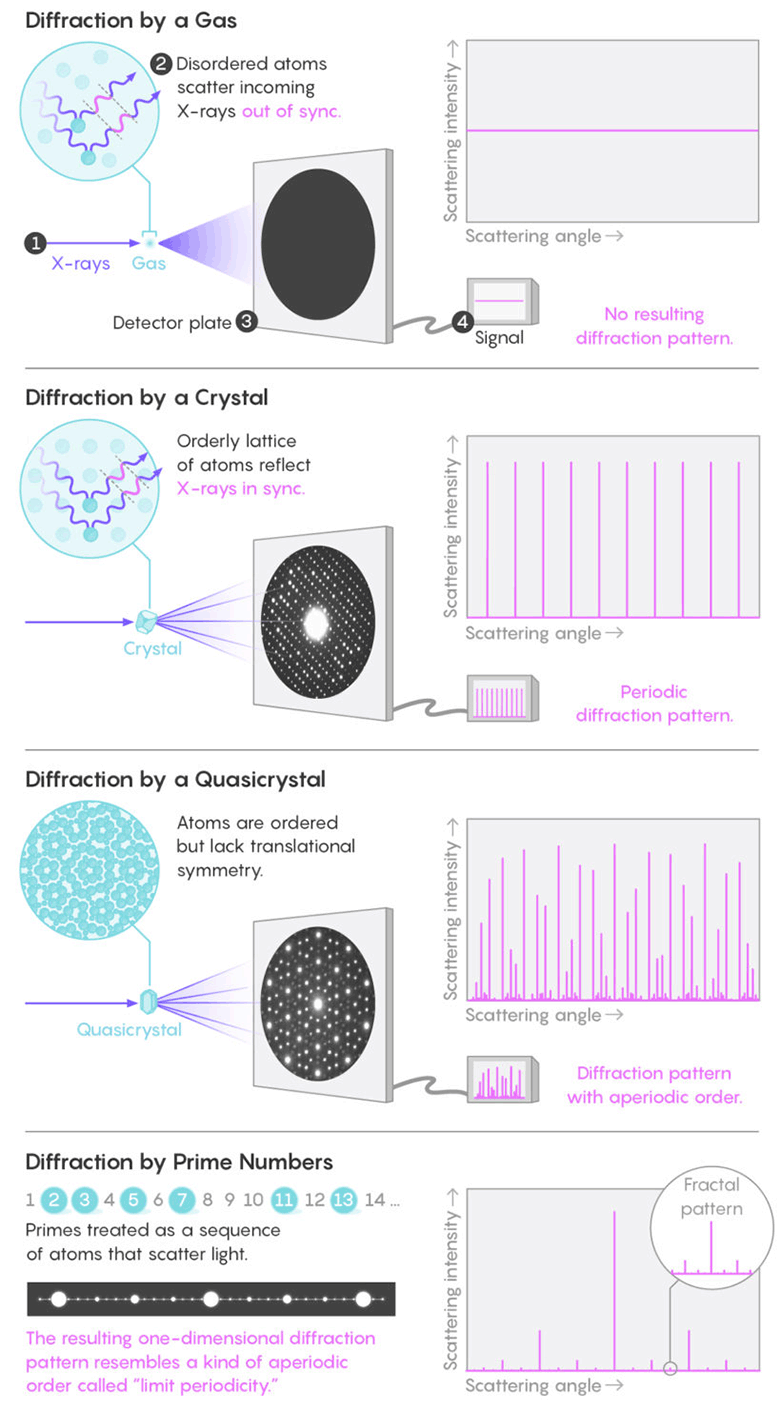Zufällige Moleküle in Flüssigkeiten oder Gasen reflektieren Strahlen in alle Richtungen, ohne ein wahrnehmbares Muster zu erzeugen. Symmetrisch angeordnete Atome in einem Kristall reflektieren jedoch synchron Lichtwellen und erzeugen periodisch helle Flecken mit ausgeprägter Beugung. Wie sich herausstellte, bildet das Verteilungsmuster von Primzahlen ein fraktales Beugungsmuster, ähnlich dem von Quasikristallen

Quasikristalle sind seltsame Materialien, die in den 1980er Jahren entdeckt wurden. Sie zeichnen sich durch in der klassischen Kristallographie verbotene Symmetrie und das Vorhandensein einer Fernordnung aus. Aperiodische Mosaike vom Typ des berühmten Penrose-Mosaiks sind ein mathematisches Modell für Quasikristalle. In diesen Mosaiken fehlt die Translationssymmetrie, Wiederholbarkeit und Quasikristallinität sind vorhanden (Symmetrie fünfter Ordnung).


Fragment des Penrose-Mosaiks Typ P1 (aus Kacheln von sechs Typen)

Bei Primzahlen sind die Abstände zwischen den Peaks im Gegensatz zu den irrational beabstandeten Bragg-Peaks von Quasikristallen proportional zueinander. "Primzahlen implizieren tatsächlich einen völlig anderen Zustand der Partikelpositionen, ähnlich wie Quasikristalle, aber nicht wie Quasikristalle", sagte Torcuato.

Die Entdeckung des Beugungsmusters kann nicht als Durchbruch für die Zahlentheorie bezeichnet werden, da der Hauptteil dieser Muster bereits zuvor nur mit anderen mathematischen Methoden (nicht durch Beugung von Quasikristallen) beschrieben wurde. Unter Verwendung des Beugungsmusters ist es also möglich, "Doppel" der Typen 17 und 19 vorherzusagen - dies ist das mathematische Äquivalent der ersten Hardy-Littlewood-Hypothese bezüglich der Existenz von Tupeln von Primzahlen auf einem gegebenen Segment der Zahlenlinie. Eine der Regeln verbietet Drillinge aufeinanderfolgender ungerader Zahlen nach {3, 5, 7}. Dies erklärt auch, warum der nächst hellere Bragg-Peak im Beugungsmuster Zahlen entspricht, die durch sechs statt vier Stellen getrennt sind.

Eine neue wissenschaftliche Arbeit ist nur ein neuer Blick auf das Problem der gleichmäßigen Verteilung von Primzahlen und eine einfachere Möglichkeit, ein bestimmtes „einheitliches Gesetz“ für sie abzuleiten. Darüber hinaus ist dies eine ungewöhnliche Methode zur Analyse eines mathematischen Problems unter dem Gesichtspunkt der Kristallographie, und zwar unter dem Gesichtspunkt eines relativ jungen Forschungsgebiets namens „aperiodische Ordnung“, das sich nicht wiederholende Modelle untersucht und an der Schnittstelle von Kristallographie, dynamischen Systemen, harmonischer Analyse und diskreter Geometrie liegt. Dieser Wissenschaftszweig wuchs nach der Entdeckung der Quasikristalle, als klar wurde, dass die alten Methoden hier nicht funktionierten.

Die Verteilung der Primzahlen ähnelt einer speziellen aperiodischen Ordnung, die seit den 1950er Jahren bekannt ist. Es wird Grenzperiodizität genannt. In solchen Systemen sind periodische Intervalle in einer unendlichen Hierarchie verschachtelt, so dass das System in jedem Intervall Teile von Mustern enthält, die nur in einem größeren Intervall wiederholt werden, wie in der Taylor-Sokolar-Kachel.


Taylor-Sokolar Fliese

Theoretische Berechnungen zeigen, dass sich die maximalen periodischen Phasen eines Stoffes in der Natur bilden können sollten, und solche Systeme können ungewöhnliche Eigenschaften haben. Aber niemand ahnte, die begrenzende Periodizität mit Primzahlen zu verbinden. Jetzt wissen wir, dass es einen solchen Zusammenhang gibt, und die Primzahlen zeigen eine neue Art von Grenzperiodizität - die „effektive“ Grenzperiodizität, da die Synchronität in den Abständen zwischen den Primzahlen im gesamten System nur statistisch beobachtet wird.

Es stellt sich die Frage: Wie können Muster in der Verteilung von Primzahlen die Stärke kryptografischer Algorithmen beeinflussen?

„Ich bekomme wirklich viele Briefe zu diesem Thema. Obwohl dies eine interessante Studie ist, hat sie nichts mit Kryptographie zu tun “, schrieb der berühmte Kryptograf Bruce Schneier in seinem Blog. - Kryptographen sind nicht daran interessiert, Primzahlen oder deren Verteilung zu finden. Die Persistenz von RSA-Typ-Kryptografiealgorithmen mit öffentlichem Schlüssel ist mit der Schwierigkeit verbunden, große zusammengesetzte Zahlen zu faktorisieren, die das Produkt von Primzahlen sind. Und das ist eine ganz andere Sache. “

Trotz der Fortschritte bei der Untersuchung der Verteilung von Primzahlen besteht noch kein Grund zur Sorge um die Stärke kryptografischer Codes.

---