Hallo allerseits! Dieser Artikel konzentriert sich auf einen wichtigen Teil der digitalen Signalverarbeitung - die Fenstersignalfilterung, insbesondere auf FPGAs. Der Artikel zeigt, wie klassische Fenster mit Standardlänge und "langen" Fenstern von 64K bis 16M + entworfen werden. Die Hauptentwicklungssprache ist VHDL, die Elementbasis sind die neuesten Xilinx FPGA-Kristalle der neuesten Familien: Ultrascale, Ultrascale +, 7-Serie. Der Artikel zeigt die Implementierung von CORDIC - dem grundlegenden Kernel zum Konfigurieren von Fensterfunktionen beliebiger Dauer sowie grundlegenden Fensterfunktionen. Der Artikel beschreibt die Entwurfsmethode unter Verwendung der Hochsprachen C / C ++ in Vivado HLS. Wie üblich finden Sie am Ende des Artikels einen Link zu den Quellcodes des Projekts.
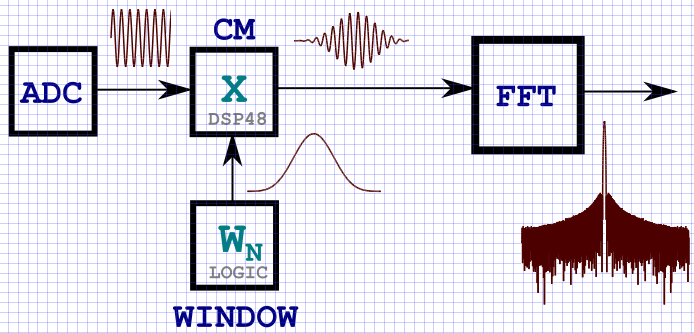
KDPV: Ein typisches Schema der Signalübertragung durch DSP-Knoten für Spektrumanalyseaufgaben.
Einführung
Aus dem Kurs „Digitale Signalverarbeitung“ wissen viele Menschen, dass für eine sinusförmige Wellenform, die zeitlich unendlich ist, ihr Spektrum eine Delta-Funktion bei der Signalfrequenz ist. In der Praxis entspricht das Spektrum eines zeitlich begrenzten harmonischen Signals der Funktion
~ sin (x) / x , und die Breite der Hauptkeule hängt von der Dauer des Signalanalyseintervalls
T ab. Das Zeitlimit ist nichts anderes als das Multiplizieren des Signals mit einer rechteckigen Hüllkurve. Aus dem DSP-Kurs ist bekannt, dass die Multiplikation von Signalen im Zeitbereich eine Faltung ihrer Spektren im Frequenzbereich ist (und umgekehrt), daher ist das Spektrum der begrenzten rechteckigen Hüllkurve des harmonischen Signals äquivalent zu ~ sinc (x). Dies liegt auch daran, dass wir das Signal nicht über ein unendliches Zeitintervall integrieren können und die Fourier-Transformation in diskreter Form, ausgedrückt durch eine endliche Summe, durch die Anzahl der Abtastwerte begrenzt ist. In der Regel nimmt die Länge der FFT in modernen digitalen FPGA-Verarbeitungsgeräten
NFFT- Werte von 8 bis zu mehreren Millionen Punkten an. Mit anderen Worten wird das Spektrum des Eingangssignals auf dem Intervall
T berechnet, das in vielen Fällen gleich
NFFT ist . Indem wir das Signal auf das Intervall
T begrenzen, legen wir dadurch ein rechteckiges "Fenster" mit einer Dauer von
T Abtastwerten fest. Daher ist das resultierende Spektrum das Spektrum des multiplizierten harmonischen Signals und der rechteckigen Hüllkurve. Bei DSP-Aufgaben wurden lange Zeit Fenster verschiedener Formen erfunden, die, wenn sie einem Signal im Zeitbereich überlagert werden, dessen spektrale Eigenschaften verbessern können. Eine große Anzahl verschiedener Fenster ist hauptsächlich auf eines der Hauptmerkmale einer Fensterüberlagerung zurückzuführen. Dieses Merkmal drückt sich in der Beziehung zwischen der Höhe der Nebenkeulen und der Breite der Mittellappen aus. Ein bekanntes Muster: Je stärker die Unterdrückung der Nebenkeulen ist, desto breiter ist die Hauptkeule und umgekehrt.
Eine der Anwendungen von Fensterfunktionen: Erkennung schwacher Signale vor dem Hintergrund stärkerer Signale durch Unterdrückung des Niveaus von Nebenkeulen. Die Hauptfensterfunktionen in DSP-Aufgaben sind ein dreieckiges, sinusförmiges Fenster, Lanczos, Hann, Hamming, Blackman, Harris, Blackman-Harris-Fenster, Flat-Top-Fenster, Natall, Gauss, Kaiser-Fenster und viele andere. Die meisten von ihnen werden durch eine endliche Reihe ausgedrückt, indem harmonische Signale mit bestimmten Gewichten summiert werden. Fenster mit komplexer Form werden mit einem Exponenten (Gaußsches Fenster) oder einer modifizierten Bessel-Funktion (Kaiser-Fenster) berechnet und in diesem Artikel nicht berücksichtigt. Sie können mehr über Fensterfunktionen in der Literatur lesen, die ich traditionell am Ende des Artikels geben werde.
Die folgende Abbildung zeigt typische Fensterfunktionen und ihre spektralen Eigenschaften, die mit Matlab CAD-Werkzeugen erstellt wurden.

Implementierung
Zu Beginn des Artikels habe ich KDPV eingefügt, das allgemein ein Strukturdiagramm der Multiplikation von Eingabedaten mit einer Fensterfunktion zeigt. Der einfachste Weg, die Speicherung einer Fensterfunktion im FPGA zu implementieren, besteht offensichtlich darin, sie in den Speicher zu schreiben (
RAMB blockieren oder verteilt
verteilen - das spielt keine Rolle) und dann die Daten zum Zeitpunkt der Eingangssignalabtastungen zyklisch abzurufen. In modernen FPGAs ermöglicht die Größe des internen Speichers in der Regel das Speichern von Fensterfunktionen relativ kleiner Größe, die dann mit den eingehenden Eingangssignalen multipliziert werden. Mit klein meine ich Fensterfunktionen mit einer Länge von bis zu 64 KB.
Was aber, wenn die Fensterfunktion zu lang ist? Zum Beispiel 1M Messwerte. Es ist leicht zu berechnen, dass für eine solche Fensterfunktion, die in einem 32-Bit-Bitgitter dargestellt wird, NRAMB = 1024 * 1024 * 32/32768 = 1024 Blockspeicherzellen der FPGA-Xilinx-Kristalle vom Typ RAMB36K erforderlich sind. Und für 16M Proben? 16 Tausend Speicherzellen! Kein einziges modernes FPGA hat so viel Speicher. Für viele FPGAs ist dies zu viel, und in anderen Fällen ist es eine verschwenderische Verwendung von FPGA-Ressourcen (und natürlich des Geldes des Kunden).
In diesem Zusammenhang müssen Sie eine Methode zum Generieren von Fensterfunktionsbeispielen direkt auf dem FPGA im laufenden Betrieb entwickeln, ohne Koeffizienten vom Remote-Gerät in den Blockspeicher schreiben zu müssen. Glücklicherweise sind die grundlegenden Dinge für uns schon lange erfunden. Mit einem Algorithmus wie
CORDIC (
Ziffernweise ) können viele Fensterfunktionen entworfen werden, deren Formeln in harmonischen Signalen ausgedrückt werden (Blackman-Harris, Hann, Hamming, Nattal usw.).
CORDIC
CORDIC ist eine einfache und bequeme iterative Methode zur Berechnung der Drehung eines Koordinatensystems, mit der Sie komplexe Funktionen berechnen können, indem Sie primitive Additions- und Verschiebungsoperationen ausführen. Mit dem CORDIC-Algorithmus kann man die Werte der harmonischen Signale sin (x), cos (x) berechnen, die Phasenatan (x) und atan2 (x, y) finden, hyperbolische trigonometrische Funktionen, den Vektor drehen, die Wurzel der Zahl extrahieren usw.
Zuerst wollte ich den fertigen CORDIC-Kernel nehmen und den Arbeitsaufwand reduzieren, aber ich habe eine lange Abneigung gegen die Xilinx-Kernel. Nachdem ich die Repositories auf dem Github studiert hatte, stellte ich fest, dass alle vorgestellten Kernel aus einer Reihe von Gründen nicht geeignet sind (schlecht dokumentiert und unlesbar, nicht universell, für eine bestimmte Aufgabe oder Elementbasis erstellt,
in Verilog geschrieben usw.). Dann bat ich Genosse
Lazifo , diese Arbeit für mich zu erledigen. Natürlich hat er damit fertig geworden, denn die Implementierung von CORDIC ist eine der einfachsten Aufgaben im Bereich DSP. Aber da ich ungeduldig bin, habe ich parallel zu seiner Arbeit
mein Fahrrad mit meinem
eigenen parametrisierten Kern geschrieben. Die Hauptmerkmale sind die konfigurierbare Bittiefe der Ausgangssignale
DATA_WIDTH und der normalisierten Eingangsphase
PHASE_WIDTH von -1 bis 1 sowie die Genauigkeit der
PRECISION- Berechnungen. Der CORDIC-Kern wird gemäß der Pipeline-Parallelschaltung ausgeführt - bei jedem Taktzyklus ist der Kern bereit, Berechnungen durchzuführen und Eingangsabtastwerte zu empfangen. Der Kernel verwendet N Zyklen, um das Ausgabesample zu berechnen, dessen Anzahl von der Kapazität der Ausgabesamples abhängt (je größer die Kapazität, desto mehr Iterationen zur Berechnung des Ausgabewerts). Alle Berechnungen erfolgen parallel. Somit ist CORDIC der Basiskern zum Erstellen von Fensterfunktionen.
Fensterfunktionen
Im Rahmen dieses Artikels realisiere ich nur jene Fensterfunktionen, die durch harmonische Signale ausgedrückt werden (Hann, Hamming, Blackman-Harris verschiedener Ordnung usw.). Was wird dafür benötigt? Im Allgemeinen sieht die Formel zum Erstellen eines Fensters wie eine Reihe endlicher Längen aus.

Ein bestimmter Satz von Koeffizienten
a k und Mitgliedern der Reihe bestimmt den Namen des Fensters. Das beliebteste und am häufigsten verwendete ist das Blackman-Harris-Fenster: unterschiedlicher Reihenfolge (von 3 bis 11). Das Folgende ist eine Koeffiziententabelle für Blackman-Harris-Fenster:

Im Prinzip ist der Blackman-Harris-Fenstersatz bei vielen Spektralanalyseproblemen anwendbar, und es besteht keine Notwendigkeit, komplexe Fenster wie Gauß oder Kaiser zu verwenden. Nattal- oder Flat-Top-Fenster sind nur eine Vielzahl von Fenstern mit unterschiedlichen Gewichten, aber denselben Grundprinzipien wie Blackman-Harris. Es ist bekannt, dass je mehr Mitglieder der Reihe, desto stärker die Unterdrückung des Pegels der Nebenkeulen ist (vorbehaltlich einer vernünftigen Wahl der Bittiefe der Fensterfunktion). Basierend auf der Aufgabe muss der Entwickler nur den verwendeten Fenstertyp auswählen.
FPGA-Implementierung - traditioneller Ansatz
Alle Kernel von Fensterfunktionen werden unter Verwendung des klassischen Ansatzes zur Beschreibung digitaler Schaltungen in FPGAs entworfen und in der VHDL-Sprache geschrieben. Unten finden Sie eine Liste der hergestellten Komponenten:
- bh_win_7term - Blackman-Harris 7-Reihenfolge, ein Fenster mit maximaler Unterdrückung von Seitengerüsten.
- bh_win_5term - Blackman-Harris 5-Bestellung, enthält ein Fenster mit einer flachen Oberseite.
- bh_win_4term - Blackman-Harris 4-Bestellungen, einschließlich der Fenster Nattal und Blackman-Nattal.
- bh_win_3term - Blackman-Harris 3 Bestellungen,
- hamming_win - Hamming und Hann Fenster.
Der Quellcode für die Blackman-Harris-Fensterkomponente beträgt 3 Größenordnungen:
entity bh_win_3term is generic ( TD : time:=0.5ns;
In einigen Fällen habe ich die
UNISIM- Bibliothek verwendet, um die
DSP48E1- und DSP48E2-Knoten in das Projekt einzubetten, wodurch
ich letztendlich die Berechnungsgeschwindigkeit aufgrund des Pipelining in diesen Blöcken erhöhen kann. Wie die Praxis gezeigt hat, ist es jedoch schneller und einfacher, freie Hand zu lassen und so etwas wie
P = zu schreiben
A * B + C und geben Sie die folgenden Anweisungen im Code an:
attribute USE_DSP of <signal_name>: signal is "YES";
Dies funktioniert gut und legt den Elementtyp fest, auf dem die mathematische Funktion für den Synthesizer implementiert ist.
Vivado hls
Außerdem habe ich alle Kerne mit den
Vivado HLS- Tools implementiert. Ich werde die
Hauptvorteile von Vivado HLS auflisten: hohe Entwurfsgeschwindigkeit (
Time-to-Market ) in Hochsprachen C oder C ++, schnelle Modellierung entwickelter Knoten aufgrund des Fehlens eines Taktfrequenzkonzepts, flexible Konfiguration von Lösungen (in Bezug auf Ressourcen und Leistung) durch Einführung Pragmas und Richtlinien im Projekt sowie eine niedrige Einstiegsschwelle für Entwickler in Hochsprachen. Der Hauptnachteil sind die suboptimalen Kosten der FPGA-Ressourcen im Vergleich zum klassischen Ansatz. Es ist auch nicht möglich, die Geschwindigkeiten zu erreichen, die durch die klassischen alten RTL-Methoden (VHDL, Verilog, SV) bereitgestellt werden. Nun, der größte
Nachteil ist das Tanzen mit einem Tamburin, aber dies ist charakteristisch für alle CAD von Xilinx. (Hinweis: Im Vivado HLS-Debugger und im tatsächlichen C ++ - Modell wurden häufig unterschiedliche Ergebnisse erzielt, da Vivado HLS die Vorteile der
willkürlichen Genauigkeit schief nutzt.)
Das folgende Bild zeigt das Protokoll des synthetisierten CORDIC-Kernels in Vivado HLS. Es ist sehr informativ und zeigt viele nützliche Informationen: die Menge der verwendeten Ressourcen, die Kernel-Benutzeroberfläche, Schleifen und ihre Eigenschaften, die Verzögerung bei der Berechnung, das Intervall für die Berechnung des Ausgabewerts (wichtig beim Entwurf von seriellen und parallelen Schaltungen):

Sie können auch sehen, wie Daten in verschiedenen Komponenten (Funktionen) berechnet werden. Es ist ersichtlich, dass in Phase Null Phasendaten gelesen werden und in den Schritten 7 und 8 das Ergebnis des CORDIC-Knotens angezeigt wird.

Das Ergebnis von Vivado HLS: Ein synthetisierter RTL-Kernel, der aus C-Code erstellt wurde. Das Protokoll zeigt, dass der Kernel in der Zeitanalyse alle Einschränkungen erfolgreich erfüllt:

Ein weiteres großes Plus von Vivado HLS ist, dass sie selbst zur Überprüfung des Ergebnisses eine Testbench des synthetisierten RTL-Codes erstellt, die auf dem Modell basiert, mit dem der C-Code überprüft wurde. Dies mag ein primitiver Test sein, aber ich glaube, dass er sehr cool und praktisch genug ist, um die Funktionsweise des Algorithmus in C und auf HDL zu vergleichen. Unten sehen Sie einen Screenshot von Vivado, der eine Simulation des Kernelfunktionsmodells einer von Vivado HLS erhaltenen Fensterfunktion zeigt:

Somit wurden für alle Fensterfunktionen unabhängig von der Entwurfsmethode ähnliche Ergebnisse erzielt - in VHDL oder in C ++. Im ersten Fall werden jedoch eine größere Betriebsfrequenz und eine geringere Anzahl von Ressourcen erreicht, und im zweiten Fall wird die maximale Entwurfsgeschwindigkeit erreicht. Beide Ansätze haben das Recht auf Leben.
Ich habe speziell berechnet, wie viel Zeit ich mit verschiedenen Methoden für die Entwicklung aufwenden würde. Ich habe ein C ++ - Projekt in Vivado HLS ~ 12-mal schneller als in VHDL implementiert.
Vergleich der Ansätze
Vergleichen Sie den Quellcode für HDL und C ++ für den CORDIC-Kern. Der Algorithmus basiert, wie bereits gesagt, auf den Operationen Addition, Subtraktion und Verschiebung. Auf VHDL sieht es so aus: Es gibt drei Datenvektoren - einer ist für die Drehung des Winkels verantwortlich, und die anderen beiden bestimmen die Länge des Vektors entlang der X- und Y-Achse, was sin und cos entspricht (siehe Bild aus dem Wiki):
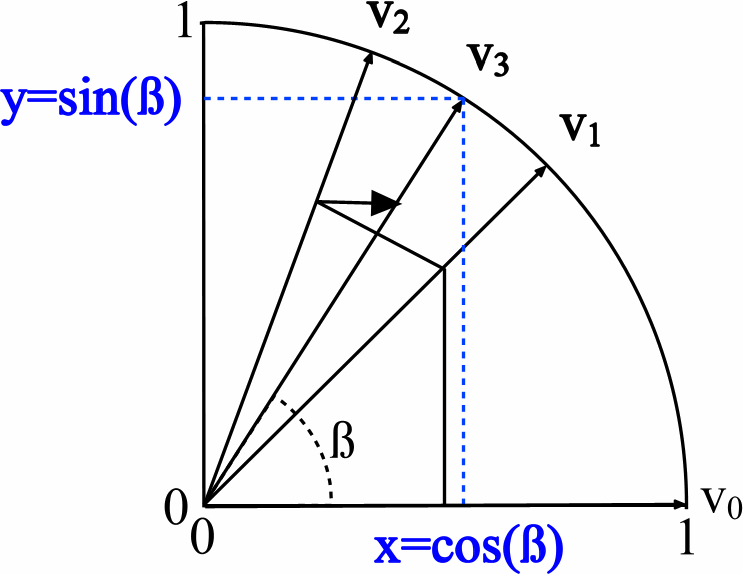
Durch iteratives Berechnen des Z-Werts werden die X- und Y-Werte parallel berechnet. Der Prozess der zyklischen Suche nach Ausgabewerten in HDL:
constant ROM_LUT : rom_array := ( x"400000000000", x"25C80A3B3BE6", x"13F670B6BDC7", x"0A2223A83BBB", x"05161A861CB1", x"028BAFC2B209", x"0145EC3CB850", x"00A2F8AA23A9", x"00517CA68DA2", x"0028BE5D7661", x"00145F300123", x"000A2F982950", x"000517CC19C0", x"00028BE60D83", x"000145F306D6", x"0000A2F9836D", x"0000517CC1B7", x"000028BE60DC", x"0000145F306E", x"00000A2F9837", x"00000517CC1B", x"0000028BE60E", x"00000145F307", x"000000A2F983", x"000000517CC2", x"00000028BE61", x"000000145F30", x"0000000A2F98", x"0000000517CC", x"000000028BE6", x"0000000145F3", x"00000000A2FA", x"00000000517D", x"0000000028BE", x"00000000145F", x"000000000A30", x"000000000518", x"00000000028C", x"000000000146", x"0000000000A3", x"000000000051", x"000000000029", x"000000000014", x"00000000000A", x"000000000005", x"000000000003", x"000000000001", x"000000000000" ); pr_crd: process(clk, reset) begin if (reset = '1') then
In C ++, in Vivado HLS, sieht der Code fast gleich aus, aber der Datensatz ist um ein Vielfaches kürzer:
Anscheinend wird der gleiche Zyklus mit Verschiebung und Hinzufügung verwendet. Standardmäßig werden jedoch alle Schleifen in Vivado HLS "reduziert" und nacheinander ausgeführt, wie für die C ++ - Sprache vorgesehen. Die Einführung des
Pragmas HLS UNROLL oder
HLS PIPELINE konvertiert serielle in parallele Berechnungen. Dies führt zu einer Erhöhung der FPGA-Ressourcen. Sie können jedoch bei jedem Taktzyklus neue Werte berechnen und an den Kern senden.
Die Ergebnisse der Synthese des Projekts in VHDL und C ++ sind in der folgenden Abbildung dargestellt. Wie Sie logischerweise sehen können, ist der Unterschied zweimal zugunsten des traditionellen Ansatzes. Bei anderen FPGA-Ressourcen ist die Diskrepanz unbedeutend. Ich habe mich nicht eingehend mit der Optimierung des Projekts in C ++ befasst, aber durch das Festlegen verschiedener Anweisungen oder das teilweise Ändern des Codes kann die Anzahl der verwendeten Ressourcen reduziert werden. In beiden Fällen konvergierten die Timings für eine gegebene Kernfrequenz von ~ 350 MHz.
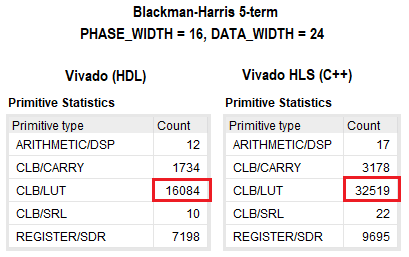
Implementierungsfunktionen
Da Berechnungen in einem Festkommaformat durchgeführt werden, weisen Fensterfunktionen eine Reihe von Merkmalen auf, die beim Entwurf von DSP-Systemen auf FPGAs berücksichtigt werden müssen. Je größer beispielsweise die Bittiefe der Fensterfunktionsdaten ist, desto besser ist die Genauigkeit der Fenstermischung. Andererseits werden bei unzureichender Bittiefe der Fensterfunktion Verzerrungen in die resultierende Wellenform eingeführt, die die Qualität der spektralen Eigenschaften beeinflussen. Beispielsweise muss eine Fensterfunktion mindestens 20 Bits haben, wenn sie mit einem Signal mit einer Dauer von 2 ^ 20 = 1 M Abtastwerten multipliziert wird.
Fazit
Dieser Artikel zeigt eine Möglichkeit zum Entwerfen von Fensterfunktionen ohne Verwendung eines externen Speichers oder eines FPGA-Blockspeichers. Die Methode zur Verwendung ausschließlich logischer Ressourcen von FPGAs (und in einigen Fällen von DSP-Blöcken) wird angegeben. Mit dem CORDIC-Algorithmus ist es möglich, Fensterfunktionen mit beliebiger Bittiefe (innerhalb eines angemessenen Rahmens), beliebiger Länge und Reihenfolge zu erhalten und daher praktisch alle spektralen Eigenschaften des Fensters zu erhalten.
Im Rahmen einer der Studien gelang es mir, einen stabil funktionierenden Kern der Blackman-Harris-Fensterfunktion von 5 und 7 Größenordnungen für 1M-Proben mit einer Frequenz von ~ 375 MHz zu erhalten und einen Generator für Rotationskoeffizienten für eine auf CORDIC basierende FFT mit einer Frequenz von ~ 400 MHz zu erstellen. Verwendeter FPGA-Kristall: Kintex Ultrascale + (xcku11p-ffva1156-2-e).
Link zum
Github- Projekt hier . Das Projekt enthält ein mathematisches Modell in Matlab, Quellcodes für Fensterfunktionen und CORDIC in VHDL sowie Modelle der aufgelisteten Fensterfunktionen in C ++ für Vivado HLS.
Nützliche Artikel
Ich empfehle auch ein sehr beliebtes Buch über DSP -
Ayficher E., Jervis B. Digitale Signalverarbeitung. Praktischer AnsatzVielen Dank für Ihre Aufmerksamkeit!