Mit LEGO EV3 entwickeln wir unbemannte Transportmittel in der High School

Robomobile ohne Fahrer liefern Pizza. Taxis ohne Fahrer befördern Menschen. Lastwagen ohne Fahrer tragen mehrere Tonnen. Wenn wir all diese spektakulären Projekte analysieren, werden wir zu verschiedenen typischen Aufgaben kommen, von denen die wichtigste die Suche und Optimierung von Routen ist. Solche Probleme werden mit der Graphentheorie gelöst. Dieses Thema ist nicht einfach, es wird hauptsächlich an der Universität oder zumindest in höheren Fachklassen studiert. Aber in diesem Beitrag werde ich zeigen, wie man mit dem LEGO EV3 bereits in der High School Graphentheorie lernt. Und ohne zu stopfen, aber auf einem faszinierenden, angewandten Niveau.


Dannys LAB EV3 Automotive Conveyor Sammelt wirklich LEGO Autos. Aber es geht nicht wenig um ihn.

Damit der unbemannte Transport dort ankommt, wo er benötigt wird, muss er in der Lage sein, eine Route zwischen den angegebenen Punkten zu erstellen. Am kürzesten und im Einklang mit den Verkehrsregeln ist wünschenswert. Um ein solches Problem zu simulieren und zu lösen, benötigen wir die mobile LEGO EV3-Plattform und tatsächlich die Karte, auf der sich diese Plattform bewegen wird.

LEGO EV3 Mobile Plattform

Unsere mobile Plattform muss mit Sensoren und Servos ausgestattet sein. Alles, was Sie brauchen, finden Sie in der Grundausbildung von LEGO Mindstorms EV3 45544. So sieht die Plattform aus:



Die Montage erfordert keine Kenntnisse der Elektronik und dauert nicht länger als eine halbe Stunde. Die Plattform bietet alles, was Sie benötigen, um bei der Lösung eines Problems ein hohes Maß an Abstraktion zu erreichen.

Straßenkarte

Zeichnen wir eine Straßenkarte in Form eines Rasters. Linien sind Straßen, Kreuzungspunkte sind Kreuzungen von Straßen:



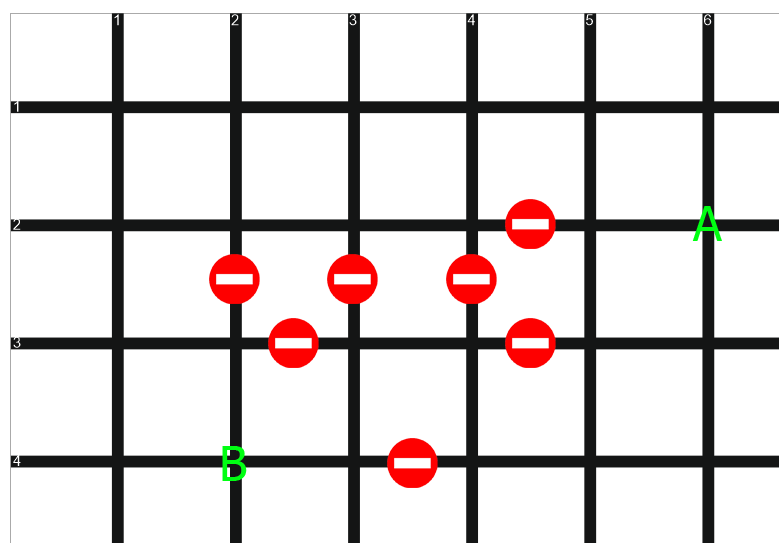
Alle Abschnitte der Straße zwischen den Kreuzungen sind gleich lang, der Verkehr auf ihnen ist in beide Richtungen. Einige Straßen sind blockiert - sie sind mit einem "Ziegelstein" markiert. Außerdem sind alle Kurven auf unserer Karte Vielfache von 90 Grad. Die Komplikation des Straßennetzes hat keinen Einfluss auf das Prinzip der Problemlösung, und aus Gründen der Klarheit werden wir eine relativ einfache Option wählen. Unsere Aufgabe ist es, auf dem kürzesten Weg von Punkt A nach Punkt B zu fahren.

Zählen

Jeder Schnittpunkt hat seine eigenen Koordinaten - die horizontalen und vertikalen Liniennummern. In der Graphentheorie werden solche Schnittpunkte als Eckpunkte bezeichnet . Straßen zwischen Kreuzungen sind durch Pfeile gekennzeichnet. In der Graphentheorie sind dies Kanten . Alle Straßen sind in beide Richtungen (Pfeile in beide Richtungen), dh der Graph ist nicht ausgerichtet . Die Kosten (Reisezeit) sind für alle Straßenabschnitte gleich, was bedeutet, dass die Grafik ungewichtet ist .

Adjazenzmatrix

Die durch das Bild dargestellte Grafik zeigt deutlich die Karte und die darin enthaltenen Verbindungen. Auf einem Computer - einschließlich EV3 - ist es jedoch mühsam, grafische Informationen zu verarbeiten. Es ist optimal, einen Graphen mit einer Matrix, einer Adjazenzmatrix, zu codieren.



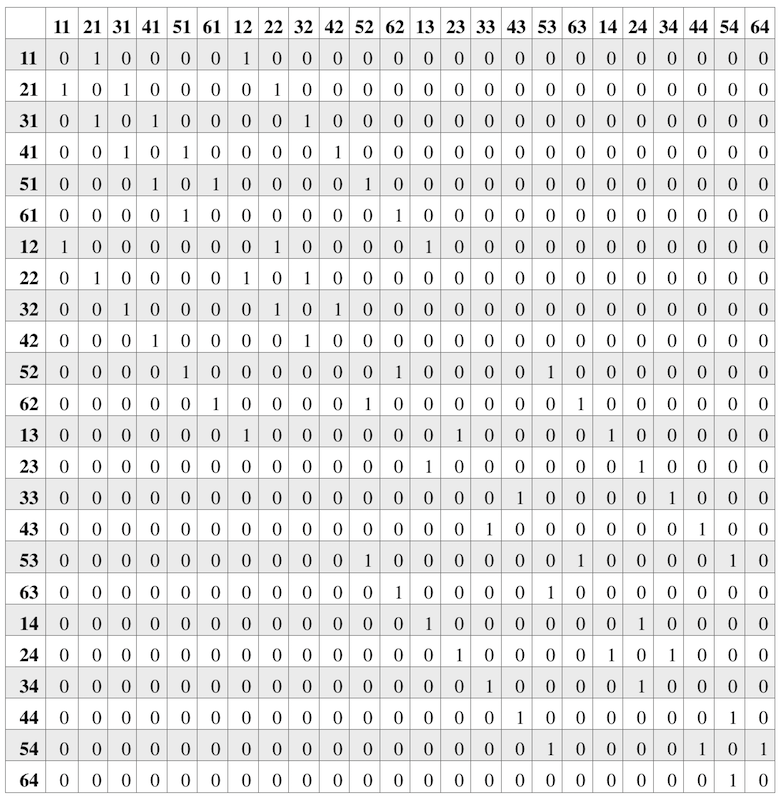
Wenn es keine direkte Verbindung zwischen den Kreuzungen gibt, setzen wir 0. Wenn es - 1 gibt. Wenn es - 1 gibt. Wir waren uns einig, dass alle Abstände zwischen benachbarten Kreuzungen gleich 1 sind. Wenn der Graph gewichtet wäre, würden wir anstelle von Eins an jeder Kreuzung „ Gewicht “der Handlung. Und wenn die Bewegungsrichtung berücksichtigt würde, wäre die obige Matrix asymmetrisch - in einer Richtung könnte sie 1 und in der anderen 0 sein.

Mit einer Adjazenzmatrix kann unser Roboter das Problem bereits lösen - den kürzesten Weg von A nach B finden. Wir haben jedoch eine zweidimensionale Matrix, und in EV3 können nur eindimensionale Arrays gespeichert werden. Wir können leicht durch die Verschiebung n * Y + X zu einem eindimensionalen Array gehen, wobei n die Größe der Matrix ist.

Dijkstra-Algorithmus

Der Dijkstra-Algorithmus, der Algorithmus zum Finden des kürzesten Pfades zwischen einem Scheitelpunkt eines Graphen und allen anderen, wird zum Lösen verwendet. Der Algorithmus wurde 1956 vom niederländischen Wissenschaftler Edsger Dijkstroy erfunden. Wenn die Erklärung so einfach wie möglich ist, basiert der Algorithmus auf dem sequentiellen Fortschritt zu benachbarten Eckpunkten des Graphen mit einer konstanten Bewertung der zurückgelegten Entfernung. Ein gutes anschauliches Beispiel und ein grundlegendes Flussdiagramm des Algorithmus finden Sie im Wikipedia-Artikel.

In unserem Fall sieht das Flussdiagramm des Dijkstra-Algorithmus (unser „Dijkstra“) folgendermaßen aus:



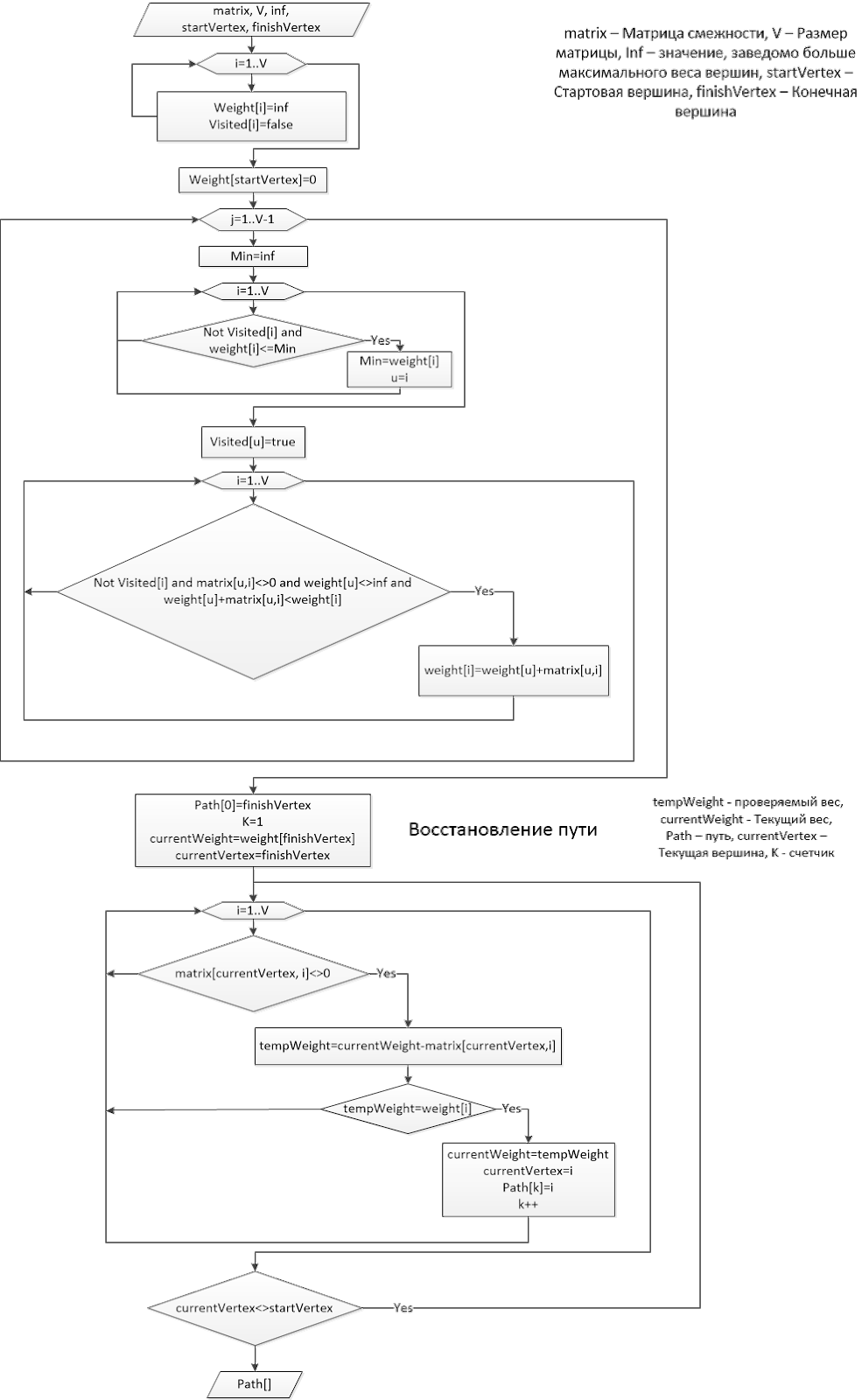
Nach dem Algorithmus und besser nach seinem mathematischen Modell können wir bereits ein Programm für den Roboter erstellen. Die Eingabe ist die Adjazenzmatrix sowie der Start- und Endpunkt. Nach allen beschriebenen Aktionen kann die Suche nach dem kürzesten Pfad zwischen Punkten auf derselben Karte schnell gefunden werden.

Zusätzlich zum Dijkstra-Algorithmus benötigt unser LEGO EV3-basierter Roboter natürlich eine Reihe einfacherer Programmmodule (Unterprogramme): Bewegen Sie sich entlang der Linie bis zur Kreuzung, zählen Sie Kreuzungen, drehen Sie sich in beide Richtungen und bestimmen Sie Ihren Standort relativ zum absoluten Koordinatensystem X, Y, Θ X, Y - Koordinaten auf dem Gitter, Θ - die aktuelle Richtung des Roboters (ausgedrückt durch den Code, zum Beispiel 1 - oben, 2 - rechts, 3 - unten, 4 - links).


Und hier ist eine Live-Demonstration der Lösung des Problems. Die Eingabedaten unterscheiden sich geringfügig, dies ändert jedoch nichts an der Essenz.

Bonus-Thema: Kilometerzähler

Odometriefunktionen können in Aufgaben zum Bewegen am Boden integriert werden - beispielsweise, damit der Roboter im Labyrinth versteht, wo er sich befindet und wo er sich bewegt. Mithilfe der Kilometerzähler wird die Bewegung des Roboters anhand von Daten zur Bewegung der Antriebe (Drehung der Motoren) geschätzt. Wenn wir den Durchmesser der Räder kennen, können wir die Entfernung berechnen, die der Roboter in einer bestimmten Zeit zurückgelegt hat. Wenn wir die Winkelgeschwindigkeit der Räder kennen, können wir den Winkel bestimmen, um den sich der Roboter relativ zum Original dreht. Durch Einstellen unterschiedlicher Winkelgeschwindigkeiten können wir die Bewegung des Roboters entlang des Bogens anpassen und gleichzeitig die „Schleifen“ beim Bewegen des Roboters bestimmen, wie im folgenden Video gezeigt:


In Schulen wird der Trigonometrie viel Aufmerksamkeit geschenkt, ihre praktische Anwendung wird jedoch in keiner Weise behandelt. Mit LEGO EV3 gelöste Odometrieprobleme zeigen, warum Trigonometrie überhaupt erforderlich sein kann. In der Praxis wird die Kilometerzähler nicht nur beim Transport eingesetzt, sondern beispielsweise auch zur Verfolgung der Position eines Werkzeugs in CNC-Maschinen (numerische Steuerung).

Wo kann ich das alles lernen?

Ich erlaube mir etwas Werbung. Die oben beschriebene Aufgabe und komplexere Aufgaben können durchaus von Kindern der Klassen 7 bis 9 gelöst werden, die in Robotikclubs ausgebildet wurden. Ich leite einen solchen Club, Robit, in Jekaterinburg - das ist unser Trainingsprogramm . Wir haben ein Video von der Demo für die obige Aufgabe in einer der Klassen gedreht. Dann studierte ein Achtklässler aus unserem Club in 6 Stunden die Grundlagen der Graphentheorie und löste ein ähnliches Problem.

So wählen Sie eine LEGO EV3-Programmierumgebung aus

Problemlösungen sind ohne die Auswahl der richtigen Programmierumgebung für LEGO EV3 nicht möglich. Spätestens in diesem Bereich gibt es separates Material . Ich versuche, Kindern beizubringen, eine Programmiersprache für die Aufgabe zu wählen, und keine Aufgabe für diese Programmiersprache, deren Syntax sie gelernt haben. In den unteren Klassen ist es jedoch schwierig, sofort in einer textbasierten Programmiersprache zu arbeiten. Daher beginnen wir, Algorithmen in Grafiksprachen zu studieren, bei denen die Eintrittsschwelle niedriger ist. Ab 10 Jahren lernen die Schüler die grafische Umgebung von EV3 Mindstorms. Einige Robotikwettbewerbe beschränken Toolkits nur auf diese Umgebung.

Ab dem 12. Lebensjahr beginnen die Jungs, die EV3 Basic-Umgebung zu beherrschen. Die Umgebung ist relativ einfach zu erlernen und Basic bietet leistungsstarke Funktionen für die LEGO EV3-Plattform. Darüber hinaus programmieren wir in der EV3Dev-Umgebung, in der Sie viele verschiedene Sprachen installieren können - Python, Java, C. Mit EV3Dev sammeln die Jungs ihre ersten Erfahrungen mit trendigen, beliebten Sprachen. Das einzige Minus von EV3Dev ist eine im Vergleich zu anderen Umgebungen relativ niedrigere Sensorabfragerate. Mit dem richtigen Ansatz wird LEGO EV3 zu einem großartigen Werkzeug, um die Programmierung kennenzulernen. Wenn Schüler sehen, wie ihr Code einem Konstruktor Leben einhaucht, ist dies eine hervorragende Motivation.

Was kommt als nächstes?

Nachdem Kinder solche Algorithmen in der High School studiert haben, können sie ihr Wissen weiter festigen und beispielsweise an Design- und Facholympiaden teilnehmen, die echte Boni bieten - zum Beispiel 100 Punkte automatisch für die Prüfung beim Eintritt in die Universität.