Die Schüler lernen das Problem der Umgehungsstraße durch die Teilnahme an Bioinformatikkursen kennen. Einer der qualitativ hochwertigsten und für Programmierer am besten geeigneten Kurse ist der Bioinformatikkurs (Pavel Pevzner) auf der Coursera der University of California in San Diego. Das Problem fällt durch die Einfachheit der Aussage, die praktische Bedeutung und die Tatsache auf, dass es immer noch als ungelöst angesehen wird und offensichtlich in der Lage ist, es mit einfacher Codierung zu lösen. Das Problem wird auf diese Weise gestellt. Ist es möglich, die Koordinaten einer Menge von Punkten
in der Polynomzeit wiederherzustellen
? $ inline $ X $ inline $ wenn die Menge aller paarweisen Abstände zwischen ihnen bekannt ist
$ inline $ \ Delta X $ inline $ ?
Diese scheinbar einfache Aufgabe steht immer noch auf der Liste der ungelösten Probleme der Rechengeometrie. Darüber hinaus betrifft die Situation nicht einmal Punkte in mehrdimensionalen Räumen, insbesondere gekrümmte, das Problem ist bereits die einfachste Option - wenn alle Punkte ganzzahlige Koordinaten haben und auf derselben Linie lokalisiert sind.
In den letzten fast einem halben Jahrhundert, seit diese Aufgabe von Mathematikern als Herausforderung erkannt wurde (Shamos, 1975), wurden einige Ergebnisse erzielt. Wir halten zwei Fälle für ein eindimensionales Problem für möglich:
- Punkte liegen auf einer geraden Linie (Turnpike-Problem)
- Punkte befinden sich auf einem Kreis (Umgehungsproblem)
Diese beiden Fälle erhielten aus einem bestimmten Grund unterschiedliche Namen - es sind unterschiedliche Anstrengungen erforderlich, um sie zu lösen. In der Tat wurde die erste Aufgabe schnell genug gelöst (in 15 Jahren) und ein Backtracking-Algorithmus wurde erstellt, der die Lösung im Durchschnitt in quadratischer Zeit wiederherstellt
$ inline $ O (n ^ 2 \ log n) $ inline $ wo
$ inline $ n $ inline $ - die Anzahl der Punkte (Skiena, 1990); Für die zweite Aufgabe wurde dies bisher nicht durchgeführt, und der am besten vorgeschlagene Algorithmus weist eine exponentielle Rechenkomplexität auf
$ inline $ O (n ^ n \ log n) $ inline $ (Lemke, 2003). Das folgende Bild zeigt eine Schätzung, wie lange Ihr Computer arbeiten wird, um eine Lösung für ein Set mit einer anderen Anzahl von Punkten zu erhalten.

Das heißt, in einer psychologisch akzeptablen Zeit (~ 10 Sekunden) können Sie viele wiederherstellen
$ inline $ X $ inline $ Bis zu 10 Tausend Punkte in einem Turnpike-Koffer und nur ~ 10 Punkte in einem Beltway-Koffer, was für praktische Anwendungen absolut wertlos ist.
Eine kleine Klarstellung. Es wird angenommen, dass das Turnpike-Problem im Hinblick auf die praktische Verwendung gelöst ist, dh für die überwiegende Mehrheit der angetroffenen Daten. In diesem Fall werden die Einwände reiner Mathematiker gegen die Tatsache, dass es spezielle Datensätze gibt, für die die Zeit, um eine Lösung zu erhalten, exponentiell ignoriert
$ inline $ O (2 ^ n \ log n) $ inline $ (Zhang, 1982). Im Gegensatz zu Turnpike kann das Umgehungsproblem mit seinem Exponentialalgorithmus in keiner Weise als gelöst angesehen werden.
Bedeutung der Lösung von Umgehungsproblemen im Hinblick auf die Bioinformatik
Ende des 20. Jahrhunderts wurde ein neuer Syntheseweg für Biomoleküle entdeckt, der als nichtribosomaler Syntheseweg bezeichnet wird. Der Hauptunterschied zum klassischen Syntheseweg besteht darin, dass das endgültige Syntheseergebnis überhaupt nicht in DNA kodiert wird. Stattdessen wird nur der Code von „Werkzeugen“ (viele verschiedene Synthetasen), die diese Objekte sammeln können, in die DNA geschrieben. Somit ist die Biomaschinentechnik erheblich angereichert, und anstelle eines einzelnen Sammlertyps (Ribosom), der nur mit 20 Standardteilen (Standardaminosäuren, auch als proteinogen bezeichnet) arbeitet, erscheinen viele andere Sammlertypen, die mit mehr als 500 Standard- und Nichtstandardteilen arbeiten können (nicht proteinogene Aminosäuren und ihre verschiedenen Modifikationen). Und diese Assembler können nicht nur Teile zu Ketten verbinden, sondern auch sehr komplizierte Strukturen erhalten - zyklisch, verzweigt sowie Strukturen mit vielen Zyklen und Verzweigungen. All dies erhöht das Arsenal der Zelle für verschiedene Fälle ihres Lebens erheblich. Die biologische Aktivität solcher Strukturen ist hoch, auch die Spezifität (Selektivität der Wirkung), eine Vielzahl von Eigenschaften ist nicht begrenzt. Die Klasse dieser Zellprodukte wird in der englischen Literatur als NRPs (nicht-ribosomale Produkte oder nicht-ribosomale Peptide) bezeichnet. Biologen hoffen, dass gerade unter solchen Produkten des Zellstoffwechsels neue pharmakologische Präparate gefunden werden können, die hochwirksam sind und aufgrund ihrer Spezifität keine Nebenwirkungen haben.
Die Frage ist nur, wie und wo nach NRPs gesucht werden soll. Sie sind sehr effektiv, daher muss die Zelle sie absolut nicht in großen Mengen produzieren, und ihre Konzentrationen sind vernachlässigbar. Daher sind chemische Extraktionsmethoden mit ihrer geringen Genauigkeit von ~ 1% und den enormen Reagenzien- und Zeitkosten nutzlos. Weiter. Sie sind nicht in DNA kodiert, was bedeutet, dass alle Datenbanken, die während der Dekodierung des Genoms akkumuliert wurden, sowie alle Methoden der Bioinformatik und Genomik ebenfalls unbrauchbar sind. Der einzige Weg, etwas zu finden, sind physikalische Methoden, nämlich Massenspektroskopie. Darüber hinaus ist das Nachweisniveau von Substanzen in modernen Spektrometern so hoch, dass unbedeutende Mengen mit insgesamt> ~ 800 Molekülen (atto-molarer Bereich oder Konzentration) gefunden werden können
$ inline $ 10 ^ {- 18} $ inline $ )
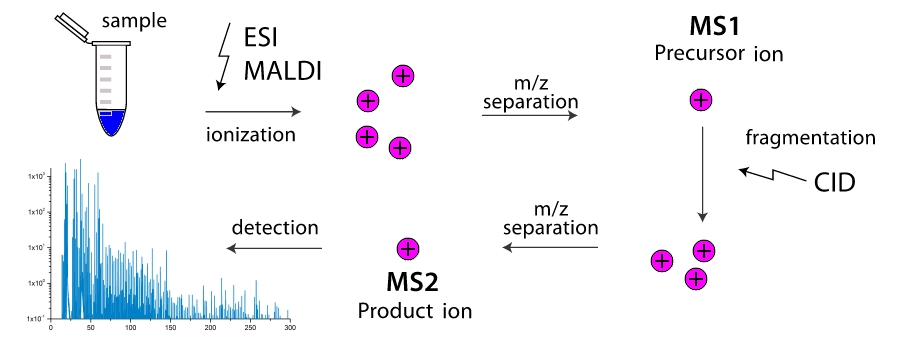
""
Wie funktioniert ein Massenspektrometer? In der Arbeitskammer des Geräts werden Moleküle in Fragmente zerlegt (häufiger durch Kollisionen miteinander, seltener durch äußere Einflüsse). Diese Fragmente werden ionisiert und dann beschleunigt und in einem externen elektromagnetischen Feld getrennt. Die Trennung erfolgt entweder durch den Zeitpunkt, zu dem der Detektor erreicht wird, oder durch den Drehwinkel im Magnetfeld, da die Masse des Fragments größer und seine Ladung geringer ist, je ungeschickter es ist. Somit "wiegt" das Massenspektrometer die Massen von Fragmenten. Darüber hinaus kann das "Wiegen" schrittweise erfolgen, indem Fragmente mit derselben Masse (genauer gesagt mit einem Wert) wiederholt gefiltert werden
$ inline $ m / z $ inline $ ) und treiben sie durch Fragmentierung mit weiterer Trennung. Zweistufige Massenspektrometer sind weit verbreitet und werden als Tandem-Massenspektrometer bezeichnet. Mehrstufige Massenspektrometer sind äußerst selten und werden einfach als bezeichnet
$ inline $ ms ^ n $ inline $ wo
$ inline $ n $ inline $ - die Anzahl der Stufen. Und hier erscheint die Aufgabe, wie man, wenn man nur die Massen aller Arten von Fragmenten eines Moleküls kennt, seine Struktur kennt? So kamen wir zu Turnpike- und Beltway-Problemen für lineare bzw. cyclische Peptide.
Ich werde am Beispiel eines cyclischen Peptids genauer erklären, wie die Aufgabe der Wiederherstellung der Struktur eines Biomoleküls auf die angegebenen Probleme reduziert wird.
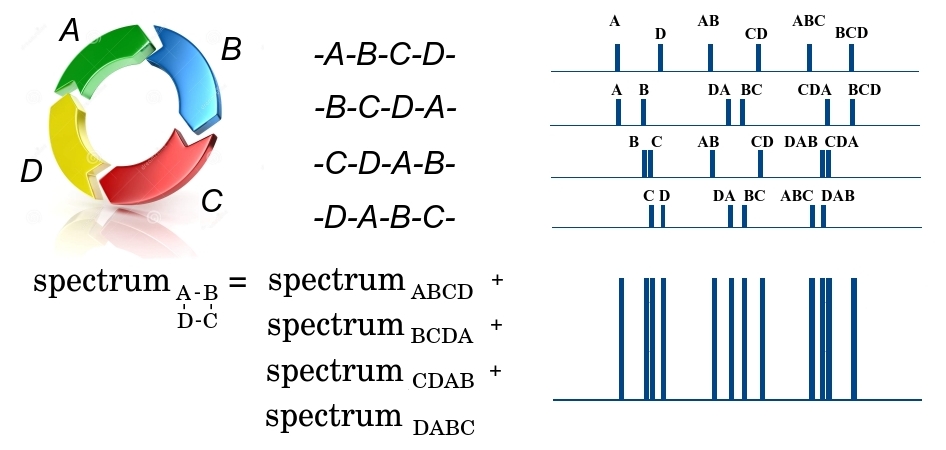
Das cyclische Peptid ABCD im ersten Stadium der Fragmentierung kann an 4 Stellen entweder durch DA-Verknüpfung oder durch AB, BC oder CD gebrochen werden, wobei 4 mögliche lineare Peptide gebildet werden - entweder ABCD, BCDA, CDAB oder DABC. Da eine große Anzahl identischer Peptide das Spektrometer passiert, werden am Ausgang Fragmente aller vier Typen vorhanden sein. Darüber hinaus stellen wir fest, dass alle Fragmente die gleiche Masse haben und im ersten Stadium nicht getrennt werden können. In der zweiten Stufe kann das lineare Fragment ABCD an drei Stellen gebrochen werden, wobei kleinere Fragmente mit unterschiedlichen Massen A und BCD, AB und CD, ABC und D gebildet werden und das entsprechende Massenspektrum gebildet wird. In diesem Spektrum ist die Fragmentmasse entlang der x-Achse und die Anzahl kleiner Fragmente mit einer gegebenen Masse entlang der y-Achse aufgetragen. In ähnlicher Weise werden Spektren für die verbleibenden drei linearen Fragmente von BCDA, CDAB und DABC gebildet. Da alle 4 großen Fragmente in die zweite Stufe übergegangen sind, werden alle ihre Spektren addiert. Insgesamt ist das Ergebnis eine gewisse Masse
$ inline $ \ {m_1 ^ {n_1}, m_2 ^ {n_2}, .., m_q ^ {n_q} \} $ inline $ wo
$ inline $ m_i $ inline $ - etwas Masse und
$ inline $ n_i $ inline $ - die Häufigkeit seiner Wiederholung. Gleichzeitig wissen wir nicht, zu welchem Fragment diese Masse gehört und ob dieses Fragment einzigartig ist, da verschiedene Fragmente eine Masse haben können. Je weiter die Bindungen im Peptid voneinander entfernt sind, desto größer ist die Masse des Peptidfragments zwischen ihnen. Das heißt, die Aufgabe, die Reihenfolge der Elemente in einem cyclischen Peptid wiederherzustellen, reduziert sich auf ein Umgehungsproblem, bei dem die Elemente des Satzes
$ inline $ X $ inline $ sind Bindungen im Peptid und Elemente einer Vielzahl
$ inline $ \ Delta X $ inline $ - Massen von Fragmenten zwischen Bindungen.
Antizipation der Existenz eines Algorithmus mit Polynomzeit zur Lösung von Umgehungsproblemen
Aus meiner Erfahrung und aus der Kommunikation mit Menschen, die versucht oder wirklich etwas getan haben, um dieses Problem zu lösen, habe ich festgestellt, dass die überwiegende Mehrheit der Menschen versucht, es entweder im allgemeinen Fall oder für ganzzahlige Daten in einem engen Bereich wie diesem zu lösen (1, 50). Beide Optionen sind zum Scheitern verurteilt. Für den allgemeinen Fall wurde nachgewiesen, dass die Gesamtzahl der Lösungen für Umgehungsprobleme im eindimensionalen Fall
$ inline $ S_1 (n) $ inline $ begrenzt durch Werte (Lemke, 2003)
$$ display $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o (1)}} \ leq S_1 (n) \ leq \ frac {1} {2} n ^ {n-2} $$ Anzeige $$
was das Vorhandensein einer exponentiellen Anzahl von Lösungen in der Asymptotik bedeutet
$ inline $ n \ rightarrow \ infty $ inline $ . Wenn die Anzahl der Lösungen exponentiell zunimmt, kann der Zeitpunkt ihres Eingangs natürlich nicht langsamer wachsen. Das heißt, für den allgemeinen Fall ist es unmöglich, eine Polynomzeitlösung zu erhalten. Bei ganzzahligen Daten in einem engen Bereich kann alles experimentell überprüft werden, da es nicht allzu schwierig ist, Code zu schreiben, der durch umfassende Suche nach einer Lösung sucht. Für kleine
$ inline $ n $ inline $ Ein solcher Code wird nicht sehr lange dauern. Die Testergebnisse eines solchen Codes zeigen, dass unter solchen Datenbedingungen die Gesamtzahl der verschiedenen Lösungen für jeden Satz
$ inline $ \ Delta X $ inline $ schon klein
$ inline $ n $ inline $ wächst auch extrem stark.
Nachdem Sie diese Fakten kennengelernt haben, können Sie diese Aufgabe aufgeben und aufgeben. Ich gebe zu, dass dies einer der Gründe ist, warum das Umgehungsproblem immer noch als ungelöst gilt. Es gibt jedoch Lücken. Denken Sie daran, dass die Exponentialfunktion
$ inline $ e ^ {\ alpha x} $ inline $ verhält sich sehr interessant. Zuerst wächst es furchtbar langsam und steigt über ein unendlich großes Intervall von 0 auf 1 an
$ inline $ \ infty $ inline $ auf 0, dann beschleunigt sich sein Wachstum immer mehr. Je niedriger jedoch der Wert
$ inline $ \ alpha $ inline $ Je größer der Wert sein sollte
$ inline $ x $ inline $ so dass das Ergebnis der Funktion über einen eingestellten Wert springt
$ inline $ y = \ xi $ inline $ . Als solcher Wert ist es bequem, eine Zahl zu wählen
$ inline $ \ xi = 2 $ inline $ Vor ihm die einzige Lösung, nach ihm gibt es viele Entscheidungen. Frage Und hat jemand die Abhängigkeit der Anzahl der Entscheidungen davon überprüft, welche Daten in die Eingabe gelangen? Ja, ich habe es getan. Es gibt eine wunderbare Doktorarbeit der kroatischen Mathematikerin Tamara Dakis (Dakic, 2000), in der sie festlegte, welche Bedingungen die Eingabedaten erfüllen müssen, damit das Problem in Polynomzeit gelöst werden kann. Die wichtigsten davon sind die Eindeutigkeit der Lösung und das Fehlen von Duplikaten im Satz der Eingabedaten
$ inline $ \ Delta X $ inline $ . Das Niveau ihrer Doktorarbeit ist sehr hoch. Es ist bedauerlich, dass sich diese Studentin nur auf ein Turnpike-Problem beschränkt hat. Ich bin überzeugt, dass dies längst gelöst gewesen wäre, wenn sie ihr Interesse an dem Umgehungsproblem gewendet hätte.
Erhalten eines Algorithmus mit Polynomzeit zur Lösung von Umgehungsproblemen
Es war möglich, die Daten zu finden, für die es möglich ist, den gewünschten Algorithmus zufällig zu erstellen. Es brauchte zusätzliche Ideen. Die Hauptidee ergab sich aus der Beobachtung (siehe oben), dass das Spektrum eines cyclischen Peptids die Summe der Spektren aller linearen Peptide ist, die bei Einzelringbrüchen gebildet werden. Da die Sequenz von Aminosäuren in einem Peptid aus einem solchen linearen Peptid wiederhergestellt werden kann, ist die Gesamtzahl der Linien im Spektrum signifikant (in
$ inline $ n $ inline $ mal wo
$ inline $ n $ inline $ - Die Anzahl der Aminosäuren im Peptid ist zu hoch. Die Frage ist nur, welche Linien aus dem Spektrum ausgeschlossen werden sollten, um die Fähigkeit zur Wiederherstellung der Sequenz nicht zu verlieren. Da beide Aufgaben (Wiederherstellung der cyclischen Peptidsequenz aus dem Massenspektrum und dem Umgehungsproblem) mathematisch isomorph sind, ist es auch möglich, viele auszudünnen
$ inline $ \ Delta X $ inline $ .
Ausdünnungsvorgänge
$ inline $ \ Delta X $ inline $ wurden unter Verwendung lokaler Symmetrien der Menge konstruiert
$ inline $ \ Delta X $ inline $ (Fomin, 2016a).
- Symmetrisierung Die erste Operation besteht darin, ein beliebiges Element der Menge auszuwählen $ inline $ x _ {\ mu} \ in \ Delta X $ inline $ und entfernen von $ inline $ \ Delta X $ inline $ alle Elemente außer denen, die symmetrische Paare in Bezug auf Punkte haben $ inline $ x _ {\ mu} / 2 $ inline $ und $ inline $ (L + x _ {\ mu}) / 2 $ inline $ wo $ inline $ L $ inline $ - Umfang (ich erinnere mich, dass sich im Umgehungsfall alle Punkte auf dem Kreis befinden).
- Teillösungsfaltung. Die zweite Operation verwendet das Rätselraten über die Lösung, dh die Kenntnis der einzelnen Punkte, die zur Lösung gehören, die sogenannte Teillösung. Von vielen $ inline $ \ Delta X $ inline $ Alle Elemente werden ebenfalls gelöscht, mit Ausnahme derjenigen, die die Bedingung erfüllen. Wenn wir den Abstand zwischen dem zu testenden Punkt und allen Punkten einer Teillösung messen, sind alle erhaltenen Werte in $ inline $ \ Delta X $ inline $ . Ich werde klarstellen, dass, wenn mindestens eine der erhaltenen Entfernungen in fehlt $ inline $ \ Delta X $ inline $ dann wird der Punkt ignoriert.
Es wurde bewiesen, dass beide Operationen die Menge verdünnen
$ inline $ \ Delta X $ inline $ Es sind jedoch noch genügend Elemente vorhanden, um die Lösung wiederherzustellen
$ inline $ X $ inline $ . Unter Verwendung dieser Operationen wurde ein Algorithmus erstellt und in c ++ implementiert, um das Umgehungsproblem zu lösen (Fomin, 2016b). Der Algorithmus unterscheidet sich kaum vom klassischen Backtracking-Algorithmus (dh wir versuchen, eine Lösung zu erstellen, indem wir mögliche Optionen aufzählen und zurückkehren, wenn während der Erstellung ein Fehler auftritt). Der einzige Unterschied besteht darin, die Menge einzugrenzen
$ inline $ \ Delta X $ inline $ uns zu testen wird deutlich weniger möglichkeiten.
Hier ist ein Beispiel dafür, wie viele
$ inline $ \ Delta X $ inline $ beim Ausdünnen.

Computerexperimente wurden für zufällig erzeugte cyclische Peptide mit einer Länge durchgeführt
$ inline $ n $ inline $ 10 bis 1000 Aminosäuren (die Ordinatenachse auf einer logarithmischen Skala). Die Abszisse zeigt auch auf einer logarithmischen Skala die Anzahl der Elemente in den Mengen, die durch verschiedene Operationen ausgedünnt wurden
$ inline $ \ Delta X $ inline $ in Einheiten
$ inline $ n $ inline $ . Eine solche Darstellung ist absolut ungewöhnlich, daher werde ich entschlüsseln, wie sie an einem Beispiel gelesen wird. Wir sehen uns das linke Diagramm an. Lassen Sie das Peptid eine Länge haben
$ inline $ n = 100 $ inline $ . Für ihn die Anzahl der Elemente im Set
$ inline $ \ Delta X $ inline $ gleich
$ inline $ n ^ 2 = 10000 $ inline $ (Dies ist ein Punkt auf der oberen gestrichelten Linie
$ inline $ y = n ^ 2 $ inline $ ) Nach dem Entfernen aus dem Set
$ inline $ \ Delta X $ inline $ sich wiederholende Elemente, Anzahl der Elemente in
$ inline $ \ Delta X $ inline $ sinkt auf
$ inline $ n_D \ ca. n ^ {1.9} \ ca. 6300 $ inline $ (Kreise mit Kreuzen). Nach der Symmetrisierung sinkt die Anzahl der Elemente auf
$ inline $ n_S \ ca. n ^ {1,75} \ ca. 3100 $ inline $ (schwarze Kreise) und nach Faltung durch Teillösung zu
$ inline $ n_C \ ca. n ^ {1.35} \ ca. 500 $ inline $ (Kreuze). Total, das Gesamtvolumen des Sets
$ inline $ \ Delta X $ inline $ nur um das 20-fache reduziert. Für ein Peptid gleicher Länge, aber im rechten Diagramm, kommt die Kontraktion von
$ inline $ n ^ 2 = 10000 $ inline $ vorher
$ inline $ N_C \ ca. n \ ca. 100 $ inline $ das heißt 100 mal.
Beachten Sie, dass die Generierung von Testfällen für das linke Diagramm so durchgeführt wird, dass der Grad der Duplizierung erreicht wird
$ inline $ k_ {dup} $ inline $ in
$ inline $ \ Delta X $ inline $ lag im Bereich von 0,1 bis 0,3 und rechts - weniger als 0,1. Der Grad der Duplizierung ist definiert als
$ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ wo
$ inline $ N_u $ inline $ - die Anzahl der eindeutigen Elemente im Set
$ inline $ \ Delta X $ inline $ . Eine solche Definition ergibt ein natürliches Ergebnis: Wenn keine Duplikate in der Menge vorhanden sind
$ inline $ \ Delta X $ inline $ seine Macht ist gleich
$ inline $ N_u = n ^ 2 $ inline $ und
$ inline $ k_ {dup} = 0 $ inline $ bei der maximal möglichen Vervielfältigung
$ inline $ N_u = n $ inline $ und
$ inline $ k_ {dup} = 1 $ inline $ . Wie man es ermöglicht, eine andere Duplizierungsstufe bereitzustellen, werde ich etwas später sagen. Die Diagramme zeigen, dass je geringer der Duplizierungsgrad ist, desto dünner wird es
$ inline $ \ Delta X $ inline $ bei
$ inline $ k_ {dup} <0.1 $ inline $ Anzahl der verdünnten Elemente
$ inline $ \ Delta X $ inline $ im Allgemeinen erreicht seine Grenze
$ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , da in der dezimierten Menge kleiner als ist
$ inline $ O (n) $ inline $ Elemente können nicht abgerufen werden (Operationen speichern genügend Elemente, um eine Lösung zu erhalten, in der
$ inline $ n $ inline $ Elemente). Die Tatsache, die Macht von einzugrenzen
$ inline $ \ Delta X $ inline $ bis zur Untergrenze ist sehr wichtig, er ist es, der zu dramatischen Änderungen in der rechnerischen Komplexität des Erhaltens einer Lösung führt.
Nach dem Einfügen von Ausdünnungsoperationen in den Backtracking-Algorithmus und dem Lösen des Umgehungsproblems wurde ein vollständiges Analogon dessen enthüllt, worüber Tamara Dakis in Bezug auf das Turnpike-Problem sprach. Lass mich dich erinnern. Sie sagte, dass es für Turnpike-Probleme möglich ist, eine Lösung in Polynomzeit zu erhalten, wenn die Lösung eindeutig ist und es keine Duplizierung gibt
$ inline $ \ Delta X $ inline $ . Es stellte sich heraus, dass ein völliges Fehlen von Duplikaten nicht erforderlich ist (für reale Daten ist dies kaum möglich). Es reicht aus, dass der Pegel recht gering sein wird. Die folgende Abbildung zeigt, wie viel Zeit erforderlich ist, um eine Lösung des Umgehungsproblems zu erhalten, abhängig von der Länge des Peptids und dem Grad der Duplikation in
$ inline $ \ Delta X $ inline $ .

In der Figur sind sowohl die Abszisse als auch die Ordinate auf einer logarithmischen Skala angegeben. So können Sie deutlich erkennen, ob die Abhängigkeit der Zählzeit von der Sequenzlänge liegt
$ inline $ T = f (n) $ inline $ Exponential (gerade Linie) oder Polynom (logarithmische Kurve). Wie in den Diagrammen zu sehen ist, wird die Lösung mit einem geringen Duplikationsgrad (rechtes Diagramm) in Polynomzeit erhalten. Genauer gesagt wird die Lösung in quadratischer Zeit erhalten. Dies tritt auf, wenn Ausdünnungsvorgänge die Leistung des Geräts auf eine Untergrenze reduzieren.
$ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ Es gibt nur noch wenige Punkte, die zurückgegeben werden, wenn das Iterieren über Optionen einzeln wird, und der Algorithmus hört im Wesentlichen auf, über Optionen zu iterieren, sondern erstellt einfach eine Lösung aus dem, was übrig bleibt.
PS Nun, ich werde das letzte Geheimnis bezüglich der Erzeugung von Sets auf verschiedenen Ebenen der Vervielfältigung enthüllen. Dies ist auf die unterschiedliche Genauigkeit der Datenpräsentation zurückzuführen. Wenn die Daten mit geringer Genauigkeit generiert werden (z. B. auf ganze Zahlen gerundet), wird der Duplizierungsgrad mit mehr als 0,3 hoch.
Wenn die Daten mit guter Genauigkeit generiert werden, beispielsweise mit bis zu 3 Dezimalstellen, nimmt der Duplizierungsgrad stark ab, weniger als 0,1. Und von hier folgt die letzte wichtige Bemerkung.Für reale Daten wird das Problem der Umgehungsstraße unter Bedingungen immer höherer Messgenauigkeit in Echtzeit lösbar.
Literatur
1. Dakic, T. (2000). Auf dem Turnpike-Problem. Doktorarbeit, Simon Fraser University.2. Fomin. E. (2016a) Ein einfacher Ansatz zur Rekonstruktion einer Menge von Punkten aus dem Multiset von n ^ 2 paarweisen Abständen in n ^ 2 Schritten für das Sequenzierungsproblem: I. Theorie. J Comput Biol. 2016, 23 (9): 769 & ndash; 75.3. Fomin. E. (2016b) Ein einfacher Ansatz zur Rekonstruktion eines Satzes von Punkten aus dem Multiset von n ^ 2 paarweisen Abständen in n ^ 2 Schritten für das Sequenzierungsproblem: II. Algorithmus. J Comput Biol. 2016, 23 (12): 934 & ndash; 942.4. Lemke, P., Skiena, S. und Smith, W. (2003). Rekonstruieren von Mengen aus Zwischenpunktabständen. Diskrete und rechnergestützte Geometriealgorithmen und Kombinatorik, 25: 597–631.5. S. Skiena, W. Smith und P. Lemke (1990). Rekonstruktion von Mengen aus Zwischenpunktabständen. In Proceedings of the Sixth ACM Symposium on Computational Geometry, S. 332–339. Berkeley, CA6. Zhang, Z. 1982. Ein exponentielles Beispiel für einen partiellen Digest-Mapping-Algorithmus. J. Comp. Biol. 1, 235–240.