Implementierung des k-means (k-means) -Algorithmus am Beispiel der Arbeit mit Pixeln

Hallo allerseits! Vor kurzem war es notwendig, Code zu schreiben, um die Bildsegmentierung unter Verwendung der k-means-Methode (englisch k-means) zu implementieren. Nun, das erste, was Google tut, ist Hilfe. Ich habe viele Informationen gefunden, beispielsweise aus mathematischer Sicht (alle Arten komplexer mathematischer Skizzen dort, Sie werden verstehen, was zum Teufel dort geschrieben steht) sowie einige Software-Implementierungen, die im englischen Internet verfügbar sind. Diese Codes sind sicherlich wunderschön - kein Zweifel, aber das Wesentliche der Idee ist schwer zu fassen. Irgendwie ist dort alles kompliziert, verwirrt und doch, von Hand, von Hand, schreiben Sie den Code nicht, Sie verstehen nichts. In diesem Artikel möchte ich eine einfache, nicht produktive, aber hoffentlich verständliche Implementierung dieses wunderbaren Algorithmus zeigen. Okay, lass uns gehen!

Was ist Clustering in Bezug auf unsere Wahrnehmungen? Lassen Sie mich ein Beispiel geben, sagen wir, es gibt ein schönes Bild mit Blumen aus dem Haus Ihrer Großmutter.



Die Frage ist: um festzustellen, wie viele Bereiche auf diesem Foto mit ungefähr derselben Farbe gefüllt sind. Nun, es ist überhaupt nicht schwierig: weiße Blütenblätter - eins, gelbe Zentren - zwei (ich bin kein Biologe, ich weiß nicht, wie sie heißen), drei grüne. Diese Abschnitte werden als Cluster bezeichnet. Ein Cluster ist eine Kombination von Daten mit gemeinsamen Merkmalen (Farbe, Position usw.). Das Bestimmen und Platzieren jeder Komponente von Daten in solchen Clustern wird als Clustering bezeichnet.

Es gibt viele Clustering-Algorithmen, aber der einfachste davon ist k - medium, worauf später noch eingegangen wird. K-means ist ein einfacher und effizienter Algorithmus, der mithilfe einer Softwaremethode einfach zu implementieren ist. Die Daten, die wir in Clustern verteilen, sind Pixel. Wie Sie wissen, besteht ein Farbpixel aus drei Komponenten: Rot, Grün und Blau. Durch das Auferlegen dieser Komponenten wird eine Palette vorhandener Farben erstellt.



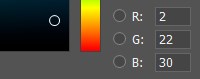
Im Speicher des Computers ist jede Farbkomponente durch eine Zahl von 0 bis 255 gekennzeichnet. Wenn Sie also verschiedene Werte für Rot, Grün und Blau kombinieren, wird eine Farbpalette auf dem Bildschirm angezeigt.

Am Beispiel von Pixeln implementieren wir unseren Algorithmus. K-means ist ein iterativer Algorithmus, dh er liefert nach einer bestimmten Anzahl von Wiederholungen einiger mathematischer Berechnungen das richtige Ergebnis.

Algorithmus

1. Sie müssen im Voraus wissen, wie viele Cluster Sie zum Verteilen der Daten benötigen. Dies ist ein wesentlicher Nachteil dieser Methode, aber dieses Problem wird durch verbesserte Implementierungen des Algorithmus gelöst, aber dies ist, wie sie sagen, eine ganz andere Geschichte.
2. Wir müssen die Anfangszentren unserer Cluster auswählen. Wie? Ja zufällig. Warum? Damit können Sie jedes Pixel in der Mitte des Clusters einrasten lassen. Das Zentrum ist wie der König, um den sich seine Motive versammeln - Pixel. Es ist der „Abstand“ von der Mitte zum Pixel, der bestimmt, wem jedes Pixel gehorcht.
3. Wir berechnen den Abstand von jedem Zentrum zu jedem Pixel. Dieser Abstand wird als euklidischer Abstand zwischen Punkten im Raum und in unserem Fall als Abstand zwischen den drei Farbkomponenten betrachtet:

   $$$$ display $$ \ sqrt {(R_ {2} -R_ {1}) ^ 2 + (G_ {2} -G_ {1}) ^ 2 + (B_ {2} -B_ {1}) ^ 2} $$ Anzeige $$

   Wir berechnen den Abstand vom ersten Pixel zu jedem Zentrum und bestimmen den kleinsten Abstand zwischen diesem Pixel und den Zentren. Für das Zentrum, dessen Abstand am kleinsten ist, berechnen wir die Koordinaten als arithmetisches Mittel zwischen jeder Komponente des Pixels - dem König und dem Pixel - des Subjekts neu. Unser Zentrum verschiebt sich nach Berechnungen im Raum.
4. Nachdem wir alle Zentren nachgezählt haben, verteilen wir die Pixel in Cluster und vergleichen den Abstand zwischen jedem Pixel und den Zentren. Ein Pixel wird in einem Cluster platziert, an dessen Zentrum es näher liegt als an den anderen Zentren.
5. Alles beginnt von vorne, solange sich die Pixel in denselben Clustern befinden. Oft kann dies nicht passieren, da sich bei einer großen Datenmenge die Zentren in einem kleinen Radius bewegen und die Pixel entlang der Kanten der Cluster in den einen oder anderen Cluster springen. Bestimmen Sie dazu die maximale Anzahl von Iterationen.

Implementierung

Ich werde dieses Projekt in C ++ implementieren. Die erste Datei ist "k_means.h", darin habe ich die Hauptdatentypen, Konstanten und die Hauptklasse für die Arbeit definiert - "K_means".
Um jedes Pixel zu charakterisieren, erstellen Sie eine Struktur, die aus drei Pixelkomponenten besteht, für die ich den Doppeltyp für genauere Berechnungen ausgewählt und einige Konstanten für das Programm definiert habe:

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb; 

K_ bedeutet Klasse selbst:

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; 

Lassen Sie uns die Komponenten der Klasse durchgehen:

vectorpixcel - ein Vektor für Pixel;
q_klaster - Anzahl der Cluster;
k_pixcel - Anzahl der Pixel;
vectorcentr - ein Vektor für Clustering-Zentren, dessen Anzahl durch q_klaster bestimmt wird;
identity_centers () - eine Methode zur zufälligen Auswahl von Anfangszentren unter den Eingabepixeln;
integrierte Methoden compute () und compute_s () zum Berechnen des Abstands zwischen Pixeln bzw. Neuberechnungszentren;
Drei Konstruktoren: Der erste dient standardmäßig zum Initialisieren von Pixeln aus einem Array, der dritte zum Initialisieren von Pixeln aus einer Textdatei (in meiner Implementierung wird die Datei zunächst versehentlich mit Daten gefüllt, und dann werden Pixel aus dieser Datei gelesen, damit das Programm funktioniert, warum nicht direkt in den Vektor - nur in meinem Fall benötigt);
Clustering (std :: ostream & os) - Clustering-Methode;
Methode und Überladung der Ausgabeanweisung zum Veröffentlichen der Ergebnisse.

Methodenimplementierung:

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } 

Dies ist eine Methode zum Auswählen der anfänglichen Clustering-Zentren und zum Hinzufügen dieser zum Center-Vektor. In diesen Fällen wird eine Überprüfung durchgeführt, um die Zentren zu wiederholen und zu ersetzen.

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } 

Eine Konstruktorimplementierung zum Initialisieren von Pixeln aus einem Array.

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } 

Wir übergeben diesem Konstruktor ein Eingabeobjekt, um Daten sowohl aus der Datei als auch aus der Konsole eingeben zu können.

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } 

Die Hauptmethode für das Clustering.

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } 

Die Ausgabe der Anfangsdaten.

Ausgabebeispiel

Dieses Beispiel ist im Voraus geplant, die Pixel werden speziell zur Demonstration ausgewählt. Zwei Iterationen reichen aus, damit das Programm die Daten in drei Cluster gruppiert. Wenn Sie sich die Zentren der letzten beiden Iterationen ansehen, können Sie sehen, dass sie praktisch an Ort und Stelle geblieben sind.

Interessanter sind die Fälle zufällig erzeugter Pixel. Nachdem ich 50 Punkte generiert hatte, die in 10 Cluster unterteilt werden müssen, erhielt ich 5 Iterationen. Nachdem ich 50 Punkte generiert habe, die in 3 Cluster unterteilt werden müssen, habe ich alle 100 maximal zulässigen Iterationen erhalten. Möglicherweise stellen Sie fest, dass es für das Programm umso einfacher ist, die ähnlichsten Pixel zu finden und zu kleineren Gruppen zu kombinieren, je mehr Cluster vorhanden sind. Wenn nur wenige Cluster und viele Punkte vorhanden sind, endet der Algorithmus häufig erst, wenn die maximale Anzahl von Iterationen überschritten wird, da einige Pixel ständig springen von einem Cluster zum anderen. Die Masse wird jedoch immer noch vollständig in ihren Clustern bestimmt.

Nun wollen wir das Ergebnis des Clusters überprüfen. Ich habe das Ergebnis einiger Cluster aus dem Beispiel von 50 Punkten pro 10 Cluster genommen und das Ergebnis dieser Daten in Illustrator übertragen. Folgendes ist passiert:



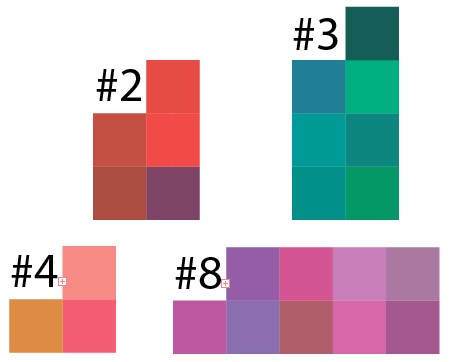
Es ist zu sehen, dass in jedem Cluster Farbtöne vorherrschen, und hier muss man verstehen, dass die Pixel zufällig ausgewählt wurden. Das Analogon eines solchen Bildes im wirklichen Leben ist eine Art Bild, auf das alle Farben versehentlich gesprüht wurden, und es ist schwierig, Bereiche mit ähnlichen Farben auszuwählen.

Nehmen wir an, wir haben so ein Foto. Wir können eine Insel als einen Cluster definieren, aber mit zunehmender Zunahme sehen wir, dass sie aus verschiedenen Grüntönen besteht.



Und dies ist Cluster 8, aber in einer kleineren Version ist das Ergebnis ähnlich:



Die Vollversion des Programms kann auf meinem GitHub eingesehen werden.