Unterhaltsame Mathematik. Das wirtschaftlichste Zahlensystem

Wir alle wissen aus dem Schulkurs, was das Zahlensystem (SS) ist. Aber nicht jeder denkt darüber nach, wie viel die SS kostet. Das heißt, Welchen Satz von Zahlen brauchen wir, um die Zahl in dieser SS darzustellen? Wenn wir eine begrenzte Anzahl einzigartiger Elemente (mehrfarbige Kieselsteine ​​unterschiedlicher Größe) haben, mit denen wir eine Zahl darstellen können, wie viele können wir mit diesen Elementen maximal darstellen? (Alle roten Kieselsteine ​​sind Null, Grün sind Eins, Blau sind Zwei usw., Klein sind Null, Mittel sind die Ersten, Groß sind die Zweiten usw.). Wo ist die Linie, an der die Basis der SS eine größere Rolle spielt als die Ziffernkapazität der Nummer?

Nehmen wir zum Beispiel n - die Anzahl der Elemente ist gleich 60. Nachdem wir die Elemente in 2 Gruppen unterteilt haben (Binärzahlensystem), erhalten wir 30 Ziffern. 30 Einheiten ist die größte 30-Bit-Zahl mit einer Basis von 2. Wenn Sie 1 hinzufügen, erhalten Sie eine Einheit mit 30 Nullen, d. H. 2 in der 30., da jede Null eine Zweierpotenz ist und die Ziffern bei 0 beginnen, und vergessen Sie nicht, die hinzugefügte Einheit zu subtrahieren.

Für andere SS ähnlich $$$y = x ^ {60 / x} -1$ Dabei ist y die maximale Anzahl, x die Basis des Grades.

Punkte erstellen:

$$$2 ^ {30} -1 = 1 \, 073 \, 741 \, 823$ .
$$$3 ^ {20} -1 = 3 \, 486 \, 784 \, 400$ .
$$$4 ^ {15} -1 = 1 \, 073 \, 741 \, 823$
$$$5 ^ {12} -1 = 244 \, 140 \, 624$
$$$6 ^ {10} -1 = 60 \, 466 \, $ 17$
$$$10 ^ {6} -1 = 999 \, $ 99$
$$$12 ^ {5} -1 = 248 \, $ 83$

Funktionsgraph:



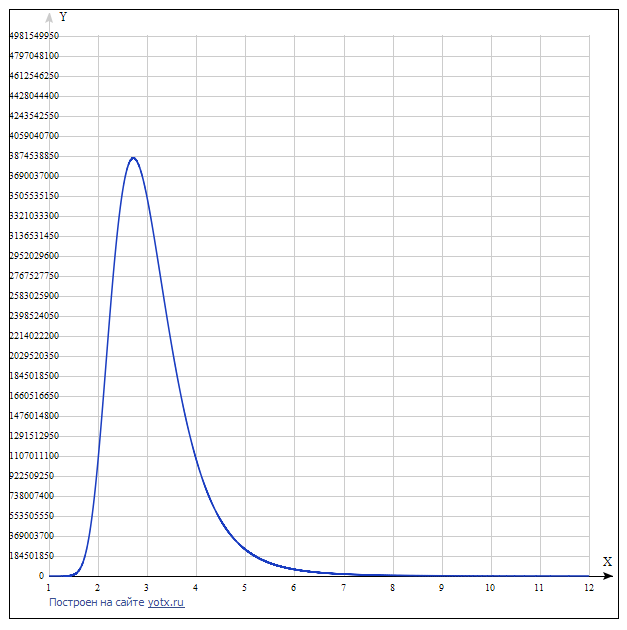
Die Grafik zeigt, dass mit einer Zunahme der Basis der SS, beginnend mit drei, ihre Kosten steigen und die Funktion ein oberes Extremum hat. Wenn Sie es in eine allgemeine Form bringen, können Sie es bekommen $$$y = (\ sqrt [x] x) ^ {n} -1$ und die maximale Funktion $$$\ sqrt [x] x$ erreicht wenn $$$x = e$ .



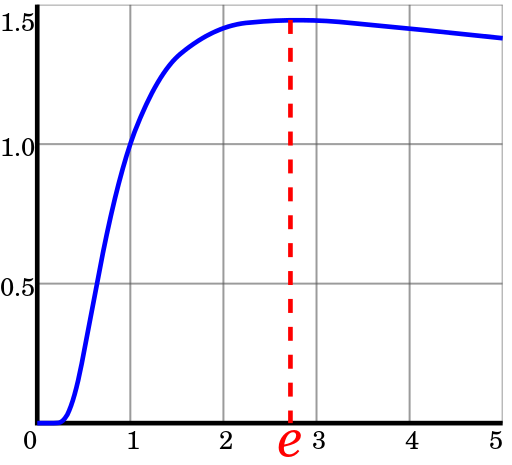
Funktionsgraph $$$y = \ sqrt [x] x$

Das heißt, Die wirtschaftlichste SS ist ein System, das so nah wie möglich ist $$$e$ oder 3.

PS: Außerdem ist die SS mit Basis 3 ungerade, was bedeutet, dass sie kein Rundungsproblem hat (bringen Sie 0,5 auf 0 oder auf 1), und wenn die Zahlen symmetrisch geschrieben sind (-1,0,1 anstelle von 0,1,2), erscheint Einfachheit stellen negative Zahlen dar (10-1 ist 8, -101 ist -8, wobei Minus kein Vorzeichen ist, sondern Teil einer Ziffer, die durch Z ersetzt werden kann), aber dies ist eine völlig andere Arithmetik)))