Wie man noch mehr ungültige Zustände noch unaussprechlicher macht

Vor nicht allzu langer Zeit wurde bei Habr ein Artikel über die Verwendung algebraischer Datentypen übersetzt, um sicherzustellen, dass falsche Zustände nicht ausgedrückt werden können. Heute schauen wir uns eine etwas allgemeinere, skalierbarere und sicherere Möglichkeit an, das Unaussprechliche auszudrücken, und das Haskell wird uns dabei helfen.

Kurz gesagt, in diesem Artikel wird eine Entität mit einer Postanschrift und einer E-Mail-Adresse sowie mit der zusätzlichen Bedingung beschrieben, dass mindestens eine dieser Adressen vorhanden sein muss. Wie wird vorgeschlagen, diese Bedingung auf Typebene auszudrücken? Es wird vorgeschlagen, die Adressen wie folgt zu schreiben:

type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo 

Welche Probleme hat dieser Ansatz?

Das offensichtlichste (und mehrfach in den Kommentaren zu diesem Artikel erwähnte) ist, dass dieser Ansatz überhaupt nicht skalierbar ist. Stellen Sie sich vor, wir haben nicht zwei Arten von Adressen, sondern drei oder fünf, und die Korrektheitsbedingung sieht so aus: "Es muss entweder eine Postanschrift oder gleichzeitig eine E-Mail-Adresse und eine Adresse im Büro vorhanden sein, und es sollten nicht mehrere Adressen desselben Typs vorhanden sein." Wer möchte, kann den entsprechenden Typ als Übung zum Selbsttest schreiben. Die Aufgabe mit einem Sternchen besteht darin, diesen Typ neu zu schreiben, wenn die Bedingung bezüglich des Fehlens von Duplikaten aus dem TOR verschwunden ist.

Teilen

Wie kann man dieses Problem lösen? Versuchen wir zu phantasieren. Zuerst zerlegen und trennen wir die Adressklasse (z. B. Mail- / E-Mail- / Schreibtischnummer im Büro) und den Inhalt, der dieser Klasse entspricht:

 data AddrType = Post | Email | Office 

Wir werden noch nicht über den Inhalt nachdenken, da in der Leistungsbeschreibung nichts für die Gültigkeit der Adressliste enthalten ist.

Wenn wir die entsprechende Bedingung zur Laufzeit eines Konstruktors einer gewöhnlichen OOP-Sprache überprüfen würden, würden wir einfach eine Funktion wie schreiben

 valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs --      hasPost = Post `elem` xs hasEmail = Email `elem` xs hasOffice = Office `elem` xs in hasNoDups && (hasPost || (hasEmail && hasOffice)) 

und würde eine Ausführung werfen, wenn es False zurückgibt.

Können wir stattdessen beim Kompilieren einen ähnlichen Zustand mit Hilfe eines Timers überprüfen? Es stellt sich heraus, dass wir es können, wenn das Typensystem der Sprache ausdrucksstark genug ist, und den Rest des Artikels werden wir diesen Ansatz wählen.

Hier helfen uns abhängige Typen sehr, und da der am besten geeignete Weg, einen validierten Code in Haskell zu schreiben, darin besteht, ihn zuerst in Agde oder Idris zu schreiben, werden wir unsere Schuhe wechseln und in Idris schreiben. Die idris-Syntax ist der von Haskell ziemlich ähnlich: Mit der oben genannten Funktion müssen Sie beispielsweise die Signatur nur geringfügig ändern:

 valid : List AddrType -> Bool 

Denken Sie nun daran, dass wir zusätzlich zu den Adressklassen auch deren Inhalt benötigen und die Abhängigkeit der Felder von der Adressklasse als GADT codieren:

 data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office 

Das heißt, wenn wir einen Wert für fields Typ AddrFields t , wissen wir, dass t eine AddrType- AddrType und dass fields eine Reihe von Feldern enthalten, die dieser bestimmten Klasse entsprechen.

 addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields 

Wie lautet die gesamte Adresse in diesem Modell? Dies ist ein Paar aus der Adressklasse und den entsprechenden Feldern:

 Addr : Type Addr = (t : AddrType ** AddrFields t) 

Fans der Typentheorie werden sagen, dass dies ein existenziell abhängiger Typ ist: Wenn wir einen Wert vom Typ Addr , bedeutet dies, dass es einen Wert t Typ AddrType und einen entsprechenden Satz von AddrFields t Feldern gibt. Adressen einer anderen Klasse sind natürlich vom gleichen Typ:

 someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762) 

Wenn uns außerdem EmailFields werden, ist die einzige geeignete EmailFields Email . Sie können sie also weglassen. Der Timer druckt sie selbst aus:

 someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762) 

Wir schreiben eine Hilfsfunktion, die die entsprechende Liste der Adressklassen aus der Adressliste angibt, und verallgemeinern sie sofort auf die Arbeit an einem beliebigen Funktor:

 types : Functor f => f Addr -> f AddrType types = map fst 

Hier verhält sich der existenzielle Addr Typ wie ein bekanntes Paar: Insbesondere können Sie nach seiner ersten Komponente AddrType (Aufgabe mit einem Sternchen: Warum kann ich nicht nach der zweiten Komponente fragen?).

Erhöhen

Jetzt kommen wir zu einem wichtigen Teil unserer Geschichte. Wir haben also eine Liste von List Addr Adressen und ein valid : List AddrType -> Bool Prädikat valid : List AddrType -> Bool , dessen Ausführung für diese Liste wir auf der Ebene der Typen garantieren möchten. Wie kombinieren wir sie? Natürlich ein anderer Typ!

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst 

Jetzt werden wir analysieren, was wir hier geschrieben haben.

data ValidatedAddrList : List Addr -> Type where bedeutet, dass der Typ ValidatedAddrList tatsächlich durch die Adressliste parametrisiert wird.

Schauen wir uns die Signatur des einzigen MkValidatedAddrList Konstruktors dieses Typs an: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst . Das heißt, es wird eine Liste von lst Adressen und ein anderes prf Argument vom Typ valid (types lst) = True . Was bedeutet dieser Typ? Dies bedeutet, dass der Wert links von = gleich dem Wert rechts von = ist, valid (types lst) , tatsächlich ist er wahr.

Wie funktioniert es Signatur = sieht aus wie (x : A) -> (y : B) -> Type . Das heißt, = nimmt zwei beliebige Werte x und y (möglicherweise sogar von unterschiedlichen Typen A und B , was bedeutet, dass die Ungleichung in der Idris heterogen ist und dass sie aus typentheoretischer Sicht etwas mehrdeutig ist, aber dies ist ein Thema für eine andere Diskussion). Was zeigt dann Gleichheit? Und aufgrund der Tatsache, dass der einzige Konstruktor = - Refl mit einer Signatur von fast (x : A) -> x = x . Das heißt, wenn wir einen Wert vom Typ x = y , wissen wir, dass er mit Refl (weil es keine anderen Konstruktoren gibt), was bedeutet, dass x tatsächlich gleich y .

Beachten Sie, dass wir deshalb in der Haskell immer bestenfalls so tun, als würden wir etwas beweisen, weil die Haskell undefined , die einen beliebigen Typ bewohnt, sodass das obige Argument dort nicht funktioniert: für jedes x , y Term vom Typ x = y könnte durch undefined (oder durch unendliche Rekursion, sagen wir, dass es im Großen und Ganzen in Bezug auf die Typentheorie dasselbe ist) erzeugt werden.

Wir stellen auch fest, dass die Gleichheit hier nicht im Sinne von Haskells Eq oder eines operator== in C ++ gemeint ist, sondern wesentlich strenger: strukturell, was vereinfachend bedeutet, dass die beiden Werte dieselbe Form haben . Das heißt, ihn so einfach zu täuschen, funktioniert nicht. Gleichstellungsfragen werden jedoch traditionell in einem separaten Artikel behandelt.

Um unser Verständnis von Gleichheit zu festigen, schreiben wir Unit-Tests für die valid Funktion:

 testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl 

Diese Tests sind insofern gut, als Sie sie nicht einmal ausführen müssen. Es reicht aus, wenn der Taypcher sie überprüft hat. Lassen Sie uns zum Beispiel im ersten Fall True durch False ersetzen und sehen, was passiert:

 testPostValid : valid [Post] = False testPostValid = Refl 

Typsekher schwört

wie erwartet. Großartig

Vereinfachen

Lassen Sie uns nun unsere ValidatedAddrList wenig umgestalten.

Erstens ist das Muster des Vergleichens eines bestimmten Werts mit True ziemlich häufig, daher gibt es dafür einen speziellen Typ So in der idris: Sie können So x als Synonym für x = True . Lassen Sie uns die Definition von ValidatedAddrList :

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst 

Darüber hinaus hat So eine bequeme Hilfsfunktion zu choose , die im Wesentlichen die Prüfung auf die Ebene der Typen erhöht:

 > :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof 

Dies ist nützlich, wenn wir Funktionen schreiben, die diesen Typ ändern.

Zweitens kann idris manchmal (insbesondere in der interaktiven Entwicklung) den entsprechenden prf Wert selbst finden. Damit es in solchen Fällen nicht von Hand konstruiert werden musste, gibt es einen entsprechenden syntaktischen Zucker:

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst 

Geschweifte Klammern bedeuten, dass dies ein implizites Argument ist, das Idris versuchen wird, aus dem Kontext herauszuziehen, und auto bedeutet, dass er auch versuchen wird, es selbst zu konstruieren.

Was bietet uns diese neue ValidatedAddrList ? Und es gibt eine solche Argumentationskette: Sei val ein Wert vom Typ ValidatedAddrList lst . Dies bedeutet, dass lst eine Liste von Adressen ist. Außerdem wurde val mit dem Konstruktor MkValidatedAddrList , an den wir lst diesen lst und einen weiteren prf Wert vom Typ So (valid $ types lst) , der fast valid (types lst) = True . Und damit wir prf bauen prf , müssen wir tatsächlich beweisen, dass diese Gleichheit gilt.

Und das Schönste ist, dass dies alles von einem Tympher überprüft wird. Ja, die Gültigkeitsprüfung muss zur Laufzeit durchgeführt werden (da die Adressen aus einer Datei oder aus dem Netzwerk gelesen werden können), aber der Timer stellt sicher, dass diese Prüfung durchgeführt wird: Ohne sie ist es unmöglich, eine ValidatedAddrList zu erstellen. Zumindest in Idris. In Haskell leider.

Einfügen

Um die Unvermeidlichkeit der Überprüfung zu überprüfen, werden wir versuchen, eine Funktion zu schreiben, um der Liste eine Adresse hinzuzufügen. Erster Versuch:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst) 

Nein, der Tippfehlerprüfer gibt an den Fingern (obwohl nicht sehr lesbar, sind die Kosten für die valid zu kompliziert):

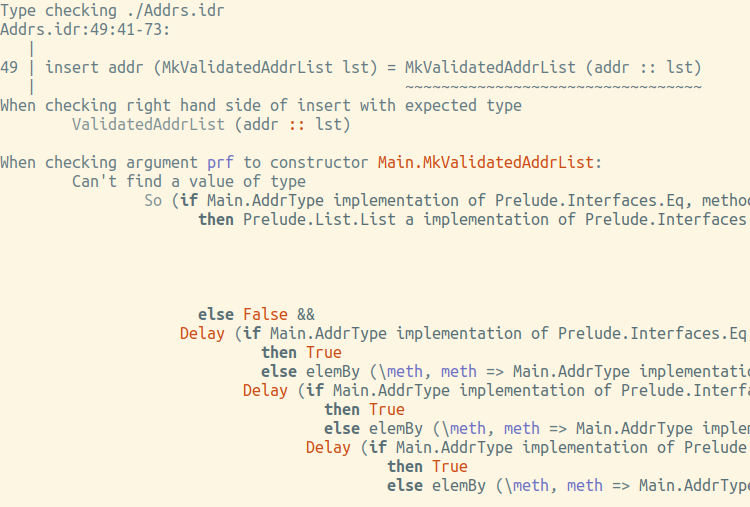
Wie bekommen wir eine Kopie dieses So ? Nicht wie oben erwähnt. Zweiter Versuch:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs 

Es ist fast typechetsya. "Fast", weil nicht klar ist, was rhs . Vielmehr ist klar: In diesem Fall muss die Funktion irgendwie einen Fehler melden. Sie müssen also die Signatur ändern und den Rückgabewert einschließen, z. B. in Maybe :

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing 

Dies ist gekachelt und funktioniert wie es sollte.

Aber jetzt tritt das folgende nicht sehr offensichtliche Problem auf, das tatsächlich im ursprünglichen Artikel war. Der Typ dieser Funktion hört nicht auf, eine solche Implementierung zu schreiben:

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing 

Das heißt, wir sagen immer, dass wir keine neue Adressliste erstellen konnten. Typhechaetsya? Ja Ist es richtig Na ja, kaum. Kann das vermieden werden?

Es stellt sich heraus, dass dies möglich ist, und wir haben alle notwendigen Werkzeuge dafür. Bei Erfolg gibt insert eine ValidatedAddrList , die Beweise für diesen Erfolg enthält. Fügen Sie also eine elegante Symmetrie hinzu und bitten Sie die Funktion, auch einen Fehlernachweis zurückzugeben!

 insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r 

Jetzt können wir nicht einfach Nothing nehmen und immer zurückgeben.

Sie können dasselbe für Funktionen zum Entfernen von Adressen und dergleichen tun.

Mal sehen, wie jetzt am Ende alles aussieht.

Versuchen wir, eine leere Adressliste zu erstellen:

Es ist unmöglich, eine leere Liste ist ungültig.

Wie wäre es mit einer Liste nur einer Postanschrift?

Okay, versuchen wir, die Postanschrift in die Liste einzufügen, die bereits die Postanschrift enthält:

Versuchen wir, die E-Mail einzufügen:

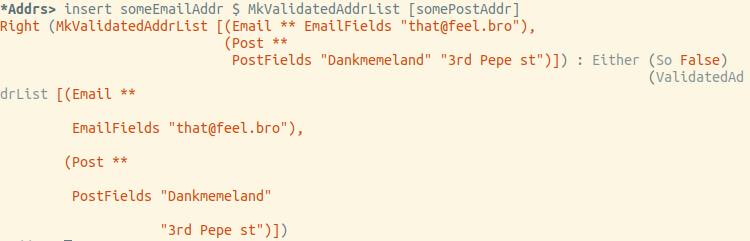
Am Ende funktioniert alles genau wie erwartet.

Puh. Ich dachte, es wären drei Zeilen, aber es stellte sich etwas länger heraus. Um herauszufinden, wie weit wir im Haskell gehen können, werden wir im nächsten Artikel sein. In der Zwischenzeit ein wenig

Nachdenken

Was ist am Ende der Gewinn einer solchen Entscheidung im Vergleich zu dem in dem Artikel, auf den wir ganz am Anfang Bezug genommen haben?

1. Es ist wiederum viel skalierbarer. Komplexe Validierungsfunktionen sind einfacher zu schreiben.
2. Es ist eher isoliert. Der Client-Code muss nicht wissen, was sich in der Validierungsfunktion befindet, während das ContactInfo Formular aus dem Originalartikel das ContactInfo erfordert.
3. Die Validierungslogik ist in Form von normalen und vertrauten Funktionen geschrieben, sodass sie sofort durch sorgfältiges Lesen überprüft und mit Tests zur Kompilierungszeit getestet werden kann, anstatt die Bedeutung der Validierung aus einem Datentypformular abzuleiten, das ein bereits verifiziertes Ergebnis darstellt.
4. Es wird möglich, das Verhalten von Funktionen, die mit dem für uns interessanten Datentyp arbeiten, genauer zu spezifizieren, insbesondere wenn der Test nicht bestanden wird. Zum Beispiel ist es einfach unmöglich, die als Ergebnis geschriebene insert falsch zu schreiben. In ähnlicher Weise könnte man insertOrReplace , insertOrIgnore und dergleichen schreiben, deren Verhalten im Typ vollständig angegeben ist.

Was ist der Gewinn im Vergleich zu einer solchen OOP-Lösung?

 class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } }; 

1. Der Code ist modularer und sicherer. Im obigen Fall ist eine Prüfung eine Aktion , die einmal geprüft wird und die sie später vergessen hat. Alles basiert auf Ehrlichkeit und dem Verständnis, dass bei einer ValidatedAddrListClass die Implementierung dort einmal überprüft wurde. Die Tatsache dieser Prüfung aus der Klasse kann nicht als bestimmter Wert herausgegriffen werden. Bei einem Wert eines bestimmten Typs kann dieser Wert zwischen verschiedenen Teilen des Programms übertragen werden, um komplexere Werte zu erstellen (z. B. diese Prüfung erneut abzulehnen), Nachforschungen anzustellen (siehe nächster Absatz) und im Allgemeinen das Gleiche wie früher zu tun mit Werten.
2. Solche Überprüfungen können beim (abhängigen) Mustervergleich verwendet werden. Richtig, nicht im Fall dieser valid Funktion und nicht im Fall von idris ist sie schmerzhaft kompliziert und idris ist schmerzhaft langweilig, so dass Informationen, die für Muster nützlich sind, aus der valid Struktur extrahiert werden können. Trotzdem kann valid in einem etwas freundlicheren Mustervergleichsstil umgeschrieben werden, aber dies geht über den Rahmen dieses Artikels hinaus und ist an sich im Allgemeinen nicht trivial.

Was sind die Nachteile?

Ich sehe nur einen schwerwiegenden Grundfehler: valid ist eine zu dumme Funktion. Es wird nur eine Information zurückgegeben - unabhängig davon, ob die Daten die Validierung bestanden haben oder nicht. Bei intelligenteren Typen könnten wir etwas Interessanteres erreichen.

Stellen Sie sich zum Beispiel vor, dass die Anforderung der Eindeutigkeit von Adressen aus TK verschwunden ist. In diesem Fall ist es offensichtlich, dass das Hinzufügen einer neuen Adresse zur vorhandenen Adressliste die Liste nicht ungültig macht. Wir könnten diesen Satz also beweisen, indem wir eine Funktion mit dem Typ So (valid $ types lst) -> So (valid $ types $ addr :: lst) und verwenden Sie es zum Beispiel, um typensicher zu schreiben, das immer erfolgreich ist

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) 

Aber leider haben Theoreme wie Rekursion und Induktion, und unser Problem hat keine elegante induktive Struktur, daher ist meiner Meinung nach der Code mit Eiche Boolean valid auch gut.