In diesem Artikel erstellen wir ein Controller-Modell, das auf der Standardbibliothek der Strukturmodellierung basiert (ohne Verwendung einer vorgefertigten Bibliothek von Fuzzy-Regelungsblöcken).
Als Steuerungsobjekt wurde ein Modell eines Gasturbinentriebwerks aus dem Lehrbuch von V.I. Gosteva „Fuzzy-Regler in automatischen Steuerungssystemen“
Vergleichen wir die PID- und SDA-Regler.
Erklärung des Problems
Der Unterschied zwischen einem Gasturbinentriebwerk (Gasturbinentriebwerk) und einem Turbostrahltriebwerk (Turbostrahltriebwerk) besteht darin, dass bei einem Gasturbinentriebwerk die gesamte Energie durch die Welle abgeführt wird. Bei Turbostrahltriebwerken wird Energie in Form eines Strahls freigesetzt.
Gasturbinentriebwerke (GTE) werden häufig in der Gas- und Luftfahrtindustrie eingesetzt, wo sie die Grundlage für Gaspumpenaggregate und Flugzeugkraftwerke bilden, für Antriebe industrieller elektrischer Turbogeneratoren von Spitzen- und Mobilkraftwerken, für Schiffskraftwerke und andere Industrieanlagen, in denen die Entwicklung großer Stückkapazitäten erforderlich ist (von 1 bis 25 MW) in einer Einheit mit minimalem Gewicht und Mindestabmessungen.
An Gasturbinentriebwerke werden eine Reihe von Anforderungen hinsichtlich ihrer Zuverlässigkeit, Energieeffizienz, Sicherheit und Umweltfreundlichkeit während des Betriebs gestellt. Neben diesen Anforderungen, den Anforderungen an die Qualität der Transienten, die mit dem Start des Geräts verbunden sind, ist eine starke Änderung der ausgewählten Last (Leistung) relevant. Die Erfüllung dieser Anforderungen liegt in vielerlei Hinsicht im automatischen Steuerungssystem (ACS) des Gasturbinentriebwerks.
Ein typisches Gasturbinentriebwerk, das in der Industrie verwendet wird, ist ein Turbowellenmotor, dessen Schaltung in Abbildung 1 dargestellt ist.
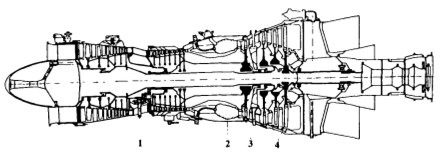
Abbildung 1. Schema eines typischen Industriegasturbinentriebwerks:
1- Kompressor; 2 - eine Brennkammer; 3 - Kompressorturbine; 4 - Leistungsturbine.
Der Motor ist eine Rotationsmaschine, bei der Luft im Kompressor 1 komprimiert wird, der der Luft zugeführte Kraftstoff in der Brennkammer 2 verbrannt wird, ein Teil der Energie aus den heißen Gasen in der Turbine des Kompressors 3 entnommen wird, die vom Antrieb des Kompressors 1 verbraucht werden, 4 Gase in der Leistungsturbine Durch die Erweiterung wird vom Verbraucher die dem Motor entnommene Leistung erzeugt.
Bei der überwiegenden Mehrheit der Gasturbinentriebwerke ist die Rotordrehzahl eine geregelte Größe. Als Steuerungsfaktor im ACS wird die Rotordrehzahl n zum Kraftstoffverbrauch GT im Brennraum verwendet. Bei verschiedenen Betriebsarten und unter verschiedenen äußeren Bedingungen ändern sich die Motorparameter erheblich.
Betrachten Sie ein Gasturbinentriebwerk (GTE) als ein nicht stationäres Steuerobjekt, für das die Rotordrehzahl n steuerbar ist und der Kraftstoffverbrauch G T die Steueraktion ist. Wenn Sie die Abhängigkeit des Turbinenmoments - M T und des Kompressormoments - M K von der Rotordrehzahl linearisieren und den Einfluss der Wärme- und Massenkapazität des Motors für einen bestimmten Betriebsmodus nicht berücksichtigen, schreiben Sie die Motorübertragungsfunktion wie folgt auf:
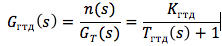
wobei die Verstärkung und die Zeitkonstante definiert sind als:
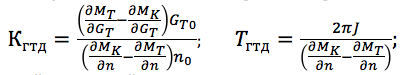
Darüber hinaus werden die Eingangs- und Ausgangssignale in relativen dimensionslosen Abweichungen vom stationären Zustand aufgezeichnet (n = Δn / n 0 ; G T = ΔG / G TO , wobei die Grundwerte der Parameter für einen bestimmten Motorbetriebsmodus ausgewählt werden, beispielsweise bewertet oder maximal). Bei verschiedenen Betriebsarten und unter verschiedenen äußeren Bedingungen ändern sich die Verstärkung und die Zeitkonstante des Motors erheblich. Daher ist es für jeden Modus erforderlich, seine eigenen Werte für K GTD und T GTD zu bestimmen.
Es ist zu beachten, dass die Übertragungsfunktion G des Gasturbinentriebwerks (der Gasturbinentriebwerke) für ein instationäres Steuerobjekt, wie beispielsweise ein Gasturbinentriebwerk, durch das Verfahren von "eingefrorenen" Koeffizienten unter der Bedingung einer ziemlich langsamen Änderung der Objektparameter erhalten wird.
Das Blockschaltbild eines analogen elektromechanischen Systems zur automatischen Steuerung der Rotordrehzahl eines Motors ist in Abbildung 2 dargestellt
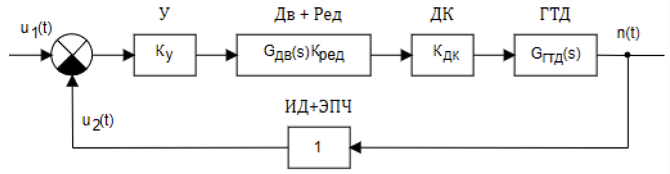
Abbildung 2. Blockdiagramm eines analogen SAR GTE
Die Rotationsfrequenz wird durch die Spannung u 1 (t) eingestellt und durch einen Impuls-ID-Sensor geändert, dessen Frequenz des Ausgangssignals durch den Ausdruck bestimmt wird:
f = kmn, wobei n die Anzahl der Motorumdrehungen ist, m die Anzahl der Zahnradzähne ist, k das Übersetzungsverhältnis ist. Die Wechselspannung, die mit dem elektronischen Frequenzumrichter des EPC vom ID-Ausgang genommen wird, wird in ein Signal u2 (t) umgewandelt, dessen Wert proportional zur Anzahl der Motorumdrehungen - n ist. Die Spannung u2 (t) wird mit der Referenzspannung und dem Fehlersignal verglichen, nachdem der Verstärker U dem Zweiphasen-Asynchronmotor Dv zugeführt wurde, der die Drosselklappe des Gleichstroms über das Getriebe Rot regelt und die Durchflussmenge des in das Gasturbinentriebwerk eintretenden Kraftstoffs ändert. Ein Impulssensor kann zusammen mit einem elektronischen Frequenzumrichter durch eine Proportionalverbindung mit einer Übertragungsfunktion gleich Eins beschrieben werden. In diesem Fall hat das System selbst eine einzige Rückmeldung.
In Anbetracht der seriellen Verbindung von Verstärker, Induktionsmotor, Drosselklappe, Gasturbineneinheit und Frequenzsensor mit einem elektronischen Frequenzumrichter als gemeinsamem Steuerobjekt und unter Verwendung eines digitalen Fuzzy-Controllers kann das gesamte Blockschaltbild aus Abbildung 2 auf das Blockschaltbild in Abbildung 3 reduziert werden Die Übertragungsfunktionen der Verbindungen werden auf eine gemeinsame Übertragungsfunktion G 0 (s) reduziert.
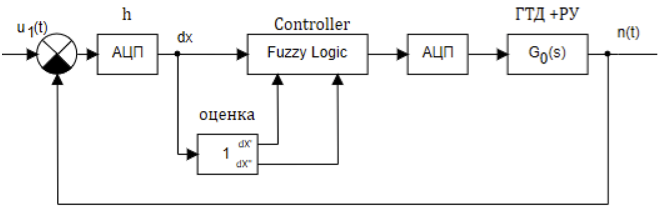
Abbildung 3. Aufbau des Steuerungssystems mit einem Fuzzy-Controller.
Die allgemeine Übertragungsfunktion G0 (s) kann wie folgt geschrieben werden:
G 0 (s) = G (s) K BEARBEITEN AUF G (s) = α [s (s + a) (s + b)] -1 , wobei
α = ab K K BEARBEITEN AUF K ,
a = 1 / T DW ,
b = 1 / T GTE
Beispielsweise nehmen wir an, dass die Abhängigkeiten der Übertragungsfunktion von der Betriebszeit folgende Werte annehmen:
T GTD (t) = 0,9849 - 0,1188 × t + 0,0063 × t 2 - 0,00012 × t 3 ;
α (t) = 16,5475 - 4,4469 × t + 0,4843 × t 2 - 0,02315 × t 3 + 0,0004 × t 4 ;
T DW = 0,35 s.
Bei der Untersuchung des Steuerungssystems nehmen wir an, dass die gegebene Funktion der Änderung der Drehzahl des Rotors eines Gasturbinentriebwerks durch die Eingangsspannung u (t) eingestellt wird.
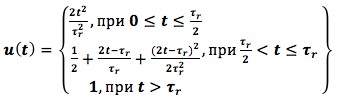
wobei τ r die Beschleunigungszeit des Motors ist. Wir nehmen τ r = 6 sec.
Erstellen eines dynamischen Modells
Ein vereinfachtes Modell des Motors ist in Abbildung 4 dargestellt. In diesem Modell verwenden wir variable Parameter typischer Blöcke, die sich während der Simulation der oben angegebenen Abhängigkeit ändern.
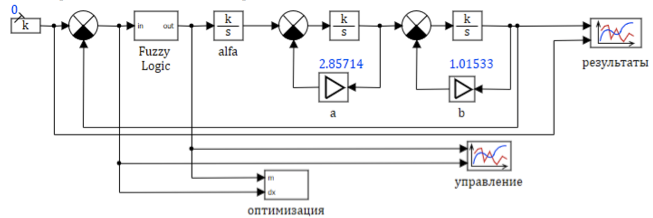
Abbildung 4. Strukturdiagramm eines Gasturbinentriebwerksmodells
Die Koeffizienten von Alfa, a, b-Verstärkern werden unter Verwendung einer Skriptsprache berechnet, der folgende Programmtext:
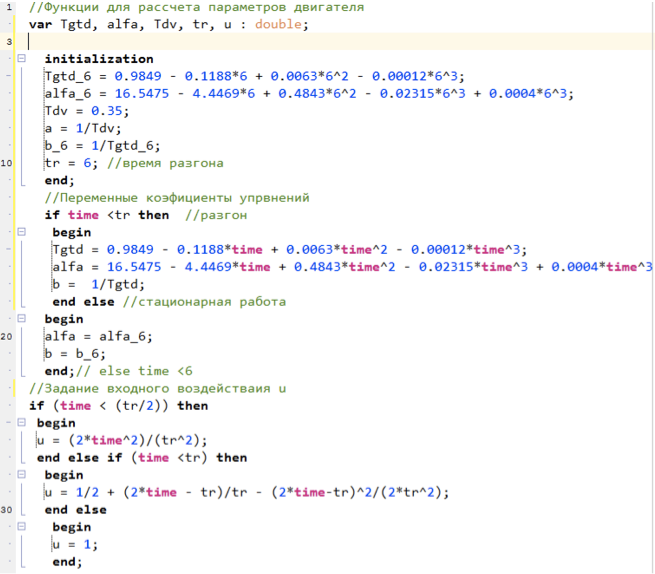
Abbildung 5. Skript zur Berechnung von Modellparametern.
Fuzzy-Logik-Steuerknopf
Der Steuerregler nimmt die Eingabe der Nichtübereinstimmung zwischen dem eingestellten Wert und dem vom Modell erhaltenen Wert entgegen und muss die Steueraktion berechnen.
Versuchen wir, einen Controller zusammenzustellen, der auf Fuzzy-Logik basiert und nur mathematisch standardmäßige Blöcke der Strukturmodellierung verwendet, ohne eine spezielle Bibliothek zu verwenden.
Eine Beschreibung der auf Fuzzy-Logik basierenden Steuerungsprinzipien finden Sie im vorherigen Artikel über den Hub oder in der Beschreibung der Erstellung einer speziellen Bibliothek von Blöcken hier (sorgfältig, Obszönität).
Jeder auf Fuzzy-Logik basierende Controller führt die folgende Folge von Transformationen durch:
- Phaseneinstellung von Eingangsvariablen. Der Wert der Variablen wird durch eine Reihe von Begriffen ersetzt.
- Aktivierung der Schlussfolgerungen der Regeln der Fuzzy-Logik.
- Ansammlung von Schlussfolgerungen für jede sprachliche Variable.
- Entnazifizierung von Ausgabevariablen.
Zur Steuerung des Motors werden drei kontinuierliche Variablen verwendet, die anhand eines Signals berechnet werden:
- Abweichung
- abgeleitete Abweichung (Änderungsrate Abweichung);
- die zweite Ableitung der Abweichung (Beschleunigung von Abweichungsänderungen).
Das Berechnungsschema ist in Abbildung 6 dargestellt:
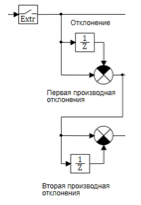
Abbildung 6. Berechnungen der Abweichungen der ersten und zweiten Ableitung.
Der Extrapolatorblock quantisiert das in die Steuerung eintretende Signal mit einer Periode von 0,01 Sekunden. Die erste und die zweite Ableitung werden unter Verwendung von Differenzformeln berechnet:
 wo:
wo:
u (t) ist die Stromabweichung zum Zeitpunkt t;
u (t - Δt) ist die Abweichung zum Zeitpunkt t - Δt;
u '(t) ist der aktuelle Wert der Ableitung der Abweichung zum Zeitpunkt t;
u '(t - Δt) ist der Wert der Ableitung der Abweichung zum Zeitpunkt t - Δt;
u '' (t) ist der aktuelle Wert der zweiten Ableitung der Abweichung zum Zeitpunkt t;
u '' (t - Δt) ist der Wert der zweiten Ableitung der Abweichung zum Zeitpunkt t - Δt;
Δt ist die Quantisierungsperiode.
Die Division durch Δt erfolgt in der Vergleichseinheit.
Als Ergebnis dieses Blocks werden drei sprachliche Variablen erstellt: Abweichung, erste Abweichungsvariable, zweite Abweichungsvariable.
Um das Problem der Fuzzy-Steuerung zu lösen, werden für jede Sprachvariable nur zwei Begriffe verwendet.
Abweichung - weniger, mehr;
Die erste Ableitung der Abweichung nimmt ab und zu;
Die zweite Ableitung der Abweichung - verlangsamt sich, beschleunigt.
Um den Wert der Zugehörigkeitsfunktion μ für jeden Term zu berechnen, verwenden wir eine lineare Funktion mit Sättigung. Diese Funktion für den Term ist größer als 0, wenn der Eingabewert minimal ist, und 1, wenn der Eingabewert maximal ist. Für einen Term weniger nimmt diese Funktion den Wert 1 an, wenn die Variable gleich dem Minimum ist, und 0, wenn die Variable maximal ist. (siehe Abb. 7)
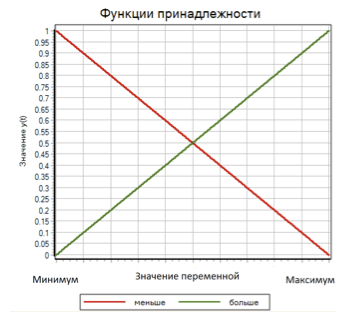
Abbildung 7. Mitgliedschaftsfunktionen für immer weniger Begriffe.
Somit gibt es für jede der drei Eingangsvariablen (Abweichung, 1. Ableitung der Abweichung, 2. Ableitung der Abweichung) mehr und weniger zwei Terme, den Wert der Zugehörigkeitsfunktionen μ i, die in Abhängigkeit vom Wert der Eingabe linear von 0 bis 1 variieren variabel.
Als sprachliche Ausgabevariable verwenden wir den Ausgabeeffekt, der auch nur zwei Begriffe zum Verringern und Erhöhen enthält.
Aus dem Modelldiagramm von Abb. 4 Es ist offensichtlich, dass wenn die Abweichung kleiner als 0 ist, der Wert größer als der angegebene Wert ist und reduziert werden muss. Wenn die Abweichung größer als 0 ist, ist die Funktion kleiner als die angegebene und muss erhöht werden.
Die logischen Regeln für die beiden Begriffe sehen folgendermaßen aus:
- Wenn weniger und abnimmt und verlangsamt => abnehmen.
- Wenn mehr und erhöht und beschleunigt => erhöhen.
Um die Fuzzy-Inferenzregeln zu aktivieren, verwenden wir die Minimalfunktion für Fuzzy und Operator. Der Wert der Zugehörigkeitsfunktionen für Terme der Ausgabefunktion wird durch die folgenden Formeln berechnet:
μ
Abnahme = MIN (μ
weniger , μ
nimmt ab , μ
verlangsamt sich )
μ
Anstieg = MIN (μ
mehr , μ
steigt , μ
beschleunigt )
Um die Umwandlung von Begriffen in bestimmte Aufprallwerte (Akkumulation und Entnazifizierung) sicherzustellen, verwenden wir den Tsukamoto-Algorithmus als Schwerpunkt der Punkte.
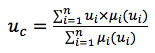 wo
wo
u c ist die resultierende Funktion;
u i ist der Wert der Funktion für Term i;
μ i ist der Wert der Zugehörigkeitsfunktion für Terme für die Funktion.
In unserem Fall wird die resultierende Funktion für zwei Terme durch die Formel berechnet:
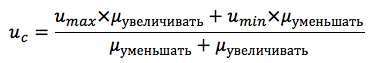
Das allgemeine Schema des Fuzzy-Inferenz-Algorithmus ist in Abbildung 8 dargestellt:
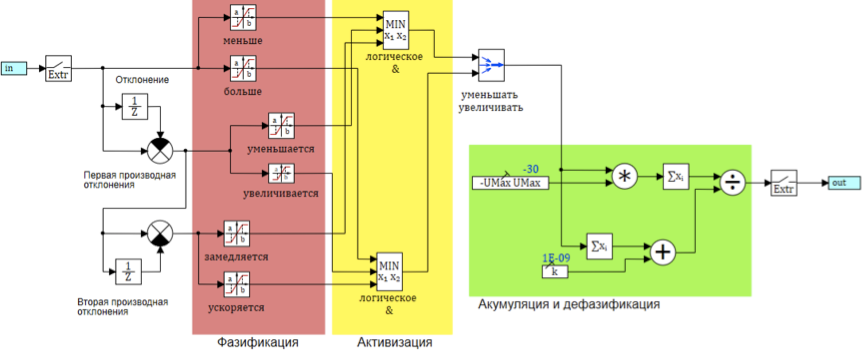
Abbildung 8. Das Schema des Fuzzy-Inferenz-Algorithmus
Damit dieser Algorithmus funktioniert, müssen wir die Minimal- und Maximalwerte für 6 Terme von drei Sprachvariablen festlegen (Abweichung, 1. Ableitung der Abweichung, 2. Ableitung der Abweichung). Um die Berechnungen zu reduzieren, nehmen wir an, dass die Abweichung in Bezug auf Null symmetrisch ist. Dann reicht es für uns, 3 Absolutwerte zu finden, einen für jede Variable.
deltMax - maximale Abweichung. Legt die Werte der Begriffe weniger, mehr fest (-deltMax, deltaMax);
divMax ist die maximale Ableitung der Abweichung. Legt fest, dass die Werte der Terme abnehmen, zunehmen (-divMax, divMax);
div2Max ist die maximale zweite Ableitung. Legt fest, dass die Werte der Begriffe verlangsamt und beschleunigt werden (-div2Max, div2Max).
Die maximale und minimale Auswirkung von umin und umax wird durch Konstruktionsmerkmale bestimmt und in diesem Beispiel mit +30 und -30 gleichgesetzt.
Einstellung des Reglers durch Optimierung.
Zur Auswahl der Koeffizienten verwenden wir dasselbe Optimierungsschema, das wir in früheren Experimenten mit Fuzzy-Logik verwendet haben.
Als Optimierungskriterium nehmen wir die Standardabweichung von nicht mehr als 0,001 und die Anzahl der Schaltvorgänge in der Steuereinheit nicht mehr als 25. Zum Schalten nehmen wir eine Änderung des Vorzeichens der Steueraktion vor.
Die Schaltung des Reglereinstellungsblocks ist in Abb. 2 dargestellt. 9.
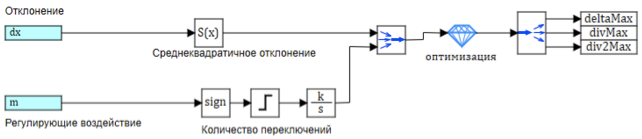
Abbildung 9. Konfigurieren der Fuzzy-Ausgabeparameter
Als Ergebnis der Blockoperation wurden die folgenden Parameter erhalten
deltMax = 0,00746;
divMax = 0,2657;
div2Max = 25,13;
Die Übergangsergebnisse sind in Abbildung 10 dargestellt.
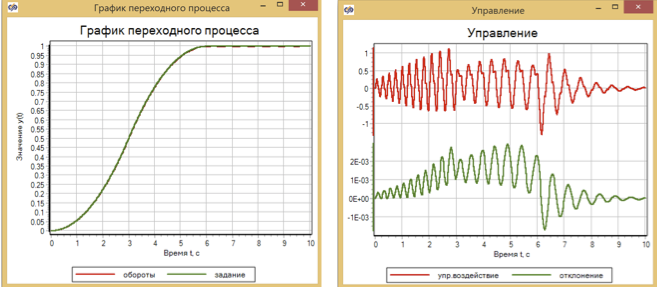
Abbildung 10. Transienten- und Motorsteuerung mithilfe von Fuzzy-Logik.
Die maximale Abweichung der Umdrehungen vom Satz nach der Optimierung betrug 2,5 × 10 –3 . Was im Prinzip nicht schlecht ist, aber im Buch von V.I. Gastabweichungen im Modell nach Einstellungen waren zwei Größenordnungen kleiner: Das Maximum betrug 5 × 10 -5 .
Zum Vergleich präsentieren wir die Ergebnisse des PID-Reglerbetriebs Abb. 11 und der Verkehrsregeln Abb. 12 für dasselbe Modell eines vereinfachten Motors. Die Parameter dieser Regler wurden ebenfalls durch die Optimierungsmethode ausgewählt.
Infolgedessen wird für den PID-Regler eine größere Abweichung erhalten als für einen Regler, der auf Fuzzy-Logik basiert - ungefähr 6 × 10 –3 , und für einen Verkehrsregler, der die zweite Ableitung verwendet, beträgt die Abweichung ungefähr 3 × 10 –3 (siehe 13). Darüber hinaus ist in allen Diagrammen zu sehen, dass sich die Qualität der Regulierung ändert, wenn sich die angegebenen Auswirkungen ändern (Änderungen in den Abschnitten 3 Sek., 6 Sek.).
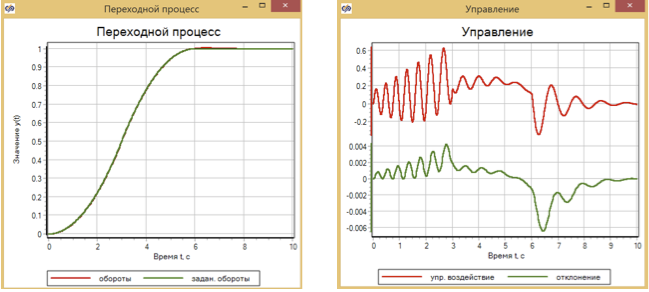
Abbildung 11. Transienten- und Motorsteuerung mit einem PID-Regler.
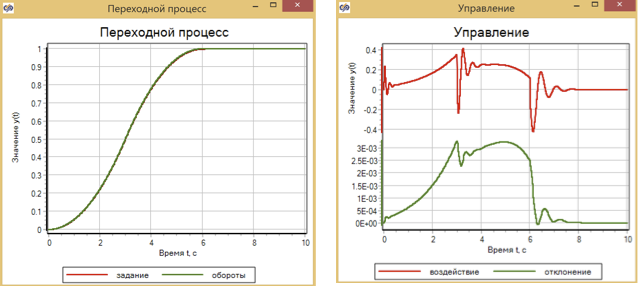
Abbildung 12. Transiente Prozess- und Motorsteuerung mit Hilfe des Verkehrsleiters.
Zum Starten des Motors wird die Übergangsfunktion in Form einer sanften Drehzahländerung verwendet. Wir haben auch die Regler durch die Optimierungsmethode für eine optimale Steuerung gemäß diesem Gesetz abgestimmt. Versuchen wir, einen schrittweisen Effekt anzuwenden und zu sehen, wie Regulierungsbehörden, die ursprünglich für einen reibungslosen Übergangsprozess optimiert wurden, damit umgehen können.
Als Effekt verwenden wir einen Schritt von 0 auf 1 nach 3 Sekunden des Prozesses.
Die Ergebnisse des Experiments sind in den Abbildungen 13-15 dargestellt.
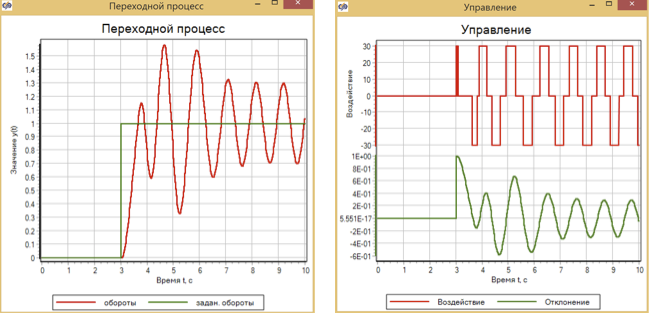
Abbildung 13. Übergangsprozess und Steuerung mit einer schrittweisen Steueraktion mit einer Fuzzy-Logik-Steuerung.
Es ist ersichtlich, dass ein Regler, der auf eine gleichmäßige Beschleunigung des Motors eingestellt ist, die Steuerung während einer schrittweisen Aktion nicht bewältigt und das System in den automatischen Oszillationsmodus wechselt.
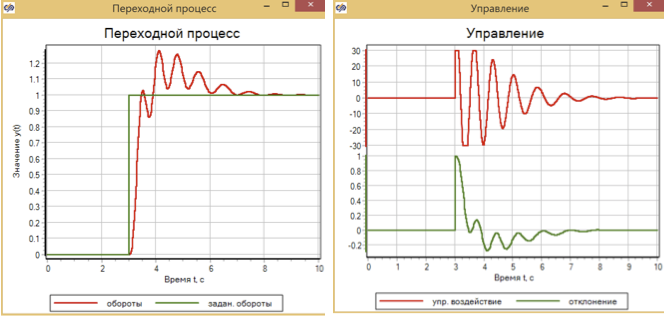
Abbildung 14. Übergangsprozess und Regelung mit Schrittregelung mit PID-Regler.
Ein PID-Regler, der auf einen reibungslosen Prozess mit schrittweisem Effekt abgestimmt ist, bietet einen Übergang zu einer vorgegebenen Zeit, gleichzeitig gibt es jedoch ein Überschwingen von 30% und einen Oszillationsprozess innerhalb von 4 Sekunden.
Der für eine reibungslose Regelung konfigurierte Verkehrsregler mit schrittweisem Effekt sorgt für einen reibungslosen Übergang ohne Überschwingen (Abb. 14).
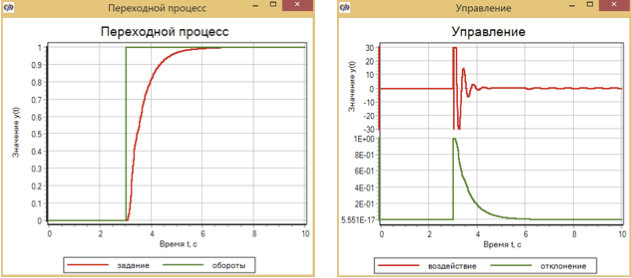
Abbildung 15. Der Übergangsprozess und die Steuerung mit einer abgestuften Steueraktion mit einer Verkehrssteuerung.
Schlussfolgerungen
Diese numerischen Experimente zeigten, dass ein auf Fuzzy-Logik basierender Regler eine genauere Steuerung der Umdrehungen eines einfachen Motormodells mit einer sanften Änderung des Einstellwerts als PID und SDA bietet.
Wie sich herausstellte, garantiert eine solche Einstellung jedoch nicht die Stabilität des Reglers während einer schrittweisen Aktion.
Gleichzeitig erwies sich für ein vereinfachtes Modell des Motors eine auf Fuzzy-Logik basierende Steuerung bei einer schrittweisen Aktion als schlechter als eine PID- oder SDA-Steuerung.
Link zum Archiv mit den Projekten aus dem Artikel zum Selbststudium