Schlaue Präfixbaum-C-Implementierung

Einführung

Seit der Veröffentlichung des Artikels über meinen Versuch, den Präfixbaum auf niedriger Ebene zu implementieren, sind vier Monate vergangen. Trotz aller Bemühungen betrug die Obergrenze, zu der sich meine vorherige Implementierung des Präfixbaums als fähig herausstellte, ~ 80.000 Wörter pro Sekunde. Ich habe dann viel Zeit und Energie aufgewendet, aber das Ergebnis wäre nur als Laborarbeit in der Informatik geeignet.

Viele sagten mir dann: „Erfinde kein Fahrrad, das wir bereits erfunden haben! Verwenden Sie die schlüsselfertige Lösung. “ Die Schwierigkeit ist, dass ich etwas nicht verwenden konnte, was ich zumindest allgemein nicht verstehe.

Ich glaube, ich habe den Präfixbaum verstanden, und das habe ich erreicht.

Arbeitsprinzip

Ich kann nicht sehr gut Englisch. Von den vielen Artikeln, die ich zum Thema Präfixbäume gelesen habe, haben mich einige Informationen wahrscheinlich nicht erreicht. Deshalb habe ich mir überlegt, wie man alles anordnet und nur das Grundprinzip des Präfixbaums versteht. Für diejenigen, die es nicht wissen, werde ich versuchen, es klarer zu beschreiben, als es auf Wikipedia geschrieben ist. Also erklärte ich meiner Frau, was ich tat.

Der Präfixbaum ist eine logische Struktur zum Speichern von Daten, die als Kartenverzeichnis von Büchern in einer Bibliothek dargestellt werden können. Jede Box hat eine Nummer. Jedes Feld entspricht einem bestimmten Buchstaben des Alphabets. Im Inneren befinden sich die Nummern der folgenden Schubladen, deren Öffnung Sie wie folgt herausfinden können und so weiter. Wenn sich nichts in der Box befindet, bedeutet dies, dass der Buchstabe dieser Box der letzte im Wort ist. Das Problem ist, dass einige Felder fast leer bleiben, da sie 1 oder 2 Zahlen enthalten und der verbleibende Platz leer ist.

Um dieses Problem zu lösen, sind viele Arten von Präfixbäumen erschienen, einschließlich: HAT-Trie, Double-Array-Trie, Tripple-Array-Trie. Es war genau die Tatsache, dass ich das Prinzip ihrer Arbeit nicht gründlich verstehen konnte, die mich zu einem Baum drängte, der so einfach war wie eine Bibliotheksausweisdatei.

Das letzte Mal gelang es mir, eine recht sparsame Implementierung eines einfachen Präfixbaums für den Speicherverbrauch zu implementieren. Ich setzte diese Metapher mit einem Bibliotheksausweis fort und fertigte Schubladen in meinem Aktenschrank in verschiedenen Größen an. Für das vollständige Alphabet ist die Box die größte, für 1 Buchstaben die kleinste.

Ich habe es geschafft, genau das gleiche PHP-Schema in C zu implementieren.

1. Jeder Buchstabe des Wortes gemäß der festgelegten Tabelle wird mit einer Zahl von 2 bis 95 codiert. Beispielsweise wird das Wort "abv" mit drei Zahlen codiert: 11, 12, 13. Für maximale Leistung wird ein zweidimensionales Array von Zahlen mit einer uint8_t abc[256][256] = {}; von 1 Byte uint8_t abc[256][256] = {}; Um ein Programm zu konvertieren, liest es eine Zeile mal 1 Byte und versucht, den Wert jedes Bytes in unserem Array zu übernehmen. Zum Beispiel ist der Zifferncode 1 = 49, also schauen wir abc[49][0]; . Wenn es einen anderen Wert als '\ 0' gibt, ist dies der Code unseres Buchstabens. Denken Sie daran und fahren Sie mit dem nächsten Byte fort. In unserem Fall besteht das Wort "abv" aus einer Folge von 6 Bytes, zwei Bytes pro Buchstabe: 208, 176, 208, 177, 208, 178. Da die utf-8-Codierung so ausgelegt ist, dass die ersten Bytes von Einzelbytezeichen niemals mit den ersten Bytes von Mehrbyte übereinstimmen in unserem Array abc[208][0] = 0; .

Für Bytepaare gibt es jedoch einige Übereinstimmungen:

 /*  [11] */ abc[208][176] = 11; /*  [12] */ abc[208][177] = 12; /*  [13] */ abc[208][178] = 13; 

2. Jetzt müssen wir die Zahlen 11, 12 und 13 in die Kästchen unseres Baumes schreiben. Der Baum besteht aus 2 separaten nicht explosiven Speicherblöcken, der erste ist ein Knotenblock, der zweite ist ein Block von Links sowie zwei Zähler von besetzten Knoten und besetzten Zellen eines Blockes von Links. Jeder Baumknoten besteht aus 16 Bytes, 12 Bytes einer Bitmaske und 4 Bytes zum Speichern der ID des Verbindungsblocks. Mit der Maske können Sie Zahlen von 2 bis 96 Bit speichern. Das erste Bit der Maske wird verwendet, um das Ende des Wortes auf diesem Knoten zu kennzeichnen. Jeder Knoten kann der ID aus dem Verbindungsblock entsprechen, wenn mindestens 1 Buchstabe in diesen Knoten geschrieben ist, oder nicht, wenn der Knoten ein "Blatt" in Bezug auf Bäume ist, dh ein Wort endet einfach darauf. Ausgedrückt in einer Bibliothek, einer leeren Schublade.

3. Nehmen Sie die Maske des ersten (Wurzel-) Knotens. trie-> node [0] .mask; Wir zählen die Bits, die in dieser Maske ausgelöst werden, beginnend mit der zweiten (die erste für das Wort-End-Flag). Wenn keine Bits in der Maske angehoben werden, d.h. Da der Knoten leer ist, benötigen wir einen Verbindungsblock der Größe 1, um unsere Nummer 11 zu speichern, die Nummer vom Verbindungsreferenzzähler des Blocks zu nehmen und den alten Wert um eins zu erhöhen (weil wir Größe 1 benötigen). Wir nehmen die Nummer vom Knotenzähler und erhöhen auch den alten Wert um 1. Wir schreiben die Verbindungsblock-ID, die die vom Verbindungsblockzähler erhaltene Nummer ist, in unseren Wurzelknoten. Schreiben Sie in diese ID des Verbindungsblocks die ID des neuen Knotens, dh die vom Knotenzähler erhaltene Nummer. Jetzt haben wir zusätzlich zum Wurzelknoten (ID 0) einen Knoten mit dem Buchstaben „a“ (ID 1). Um die Zahl 12 zu schreiben, die dem Buchstaben "b" entspricht, machen wir dasselbe, jedoch mit dem Knoten des Buchstabens "a".

4. Auf dem letzten Buchstaben "c" brauchen wir keinen Platz im Linkblock, da wir den letzten Knoten auf dem Zweig oder dem Knotenblatt haben. Ein solcher Knoten hat nur 1 Bit in der angehobenen Maske.

5. Der schwierigste Teil der Arbeit eines Baums tritt auf, wenn er auf einen Knoten geschrieben wird, in dem bereits einige Buchstaben geschrieben wurden. In diesem Fall ist das Operationsschema wie folgt:

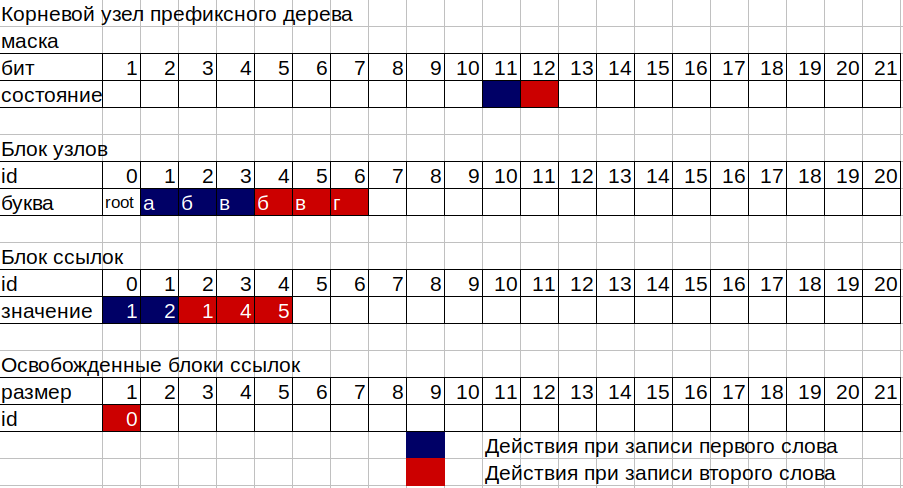
Angenommen, wir möchten unserem Baum das Wort „bvg“ (12, 13, 14) hinzufügen, in dem das Wort „abv“ (11, 12, 13) bereits geschrieben ist. Wir zählen die Bits in der Maske des Wurzelknotens bis zum Bit des für uns interessanten Buchstabens. Wir haben den Buchstaben "b" mit Code 12, was bedeutet, dass das Bit dieses Buchstabens 12 ist, in der Maske von 1 bis 12 Bit wurde Bit 11 aus dem Buchstaben "a" bereits ausgelöst. Wir haben also die aktuelle Größe des Verknüpfungsblocks für den Wurzelknoten 1. Wir schreiben den zweiten Buchstaben, also brauchen wir jetzt einen Verknüpfungsblock der Größe 2. Hier kommt die Registrierung der freigegebenen Blöcke ins Spiel, bei der die ID und Größe der Abschnitte im Verknüpfungsblock von den Knoten nicht mehr verwendet werden Baum. Unsere alte ID des Linkblocks für den Stammknoten der Größe 1 wird nur in die Registrierung der freien Abschnitte der Größe 1 aufgenommen, da unser Stammknoten eine größere Größe benötigt. Unsere Registrierung hat keinen geeigneten Abschnitt der Größe 2 und wir nehmen wieder den Wert vom Zähler des Verbindungsblocks als neue ID des Verbindungsblocks und erhöhen den Zähler um 2. An der neuen Adresse des Verbindungsblocks in derselben Reihenfolge, in der sich die Bits in der Knotenmaske befinden, schreiben wir den ID-Wert Knoten aus dem alten Linkblock für den Buchstaben "a" des ersten Wortes und den Wert des gerade erstellten Knotens des Buchstabens "b" des zweiten Wortes.

Arbeitsgeschwindigkeit

Der Drum Roll klingt ... Erinnerst du dich an das letzte Ergebnis? Ungefähr 80.000 Wörter pro Sekunde. Der Baum wurde aus dem Wörterbuch aller russischen Wörter OpenCorpora 3 039 982 Wörter erstellt. Und hier ist, was jetzt passiert ist:

 yatrie creation time: 4.588216s (666k wps) yatrie search time 1 mln. rounds: 0.565618s (1.76m wps) 

UPDATE 11/01/2018:
In Version 0.0.2 war es möglich, die Geschwindigkeit um fast das Zweifache zu erhöhen, indem vollwertige Funktionen durch Makrofunktionen ersetzt und die Struktur der Knotenmaske in uint32_t mask [3] geändert wurden, zuvor war es uint8_t mask [12].
Außerdem wurden Makros LIKELY () UNLIKELY () hinzugefügt, um die erwarteten Ergebnisse in diesen if () -Blöcken nach Möglichkeit vorherzusagen.
UPDATE 11/05/2018:
Ein bisschen mehr verdreht. Ich habe es geschafft, dass es auch beim Kompilieren von -O3 und -Ofast einwandfrei funktioniert. Die Suchgeschwindigkeit im Baum beträgt ~ 0,2 μs oder 0,2 c pro 1 Million Wiederholungen. Anscheinend wurde diese Geschwindigkeit aufgrund des Übergangs zu einem anderen Format der Maske erhalten. Früher gab es 12 Bytes mit 8 Bits und jetzt 3 int32 und eine sehr schnelle Funktion zum Zählen von Bits in int32.

Wie kompakt ist das?

Das angegebene OpenCorpora-Wörterbuch benötigt ~ 84 MB, was nicht viel schlimmer ist als libdatrie, das ~ 80 MB ergibt.

→ Quellcode

Willkommen zurück!