Implementierung des Levenberg-Marquardt-Algorithmus zur Optimierung neuronaler Netze auf TensorFlow

Dies ist ein Tutorial für die TensorFlow-Bibliothek. Betrachten Sie es als etwas tiefer als in Artikeln über das Erkennen handgeschriebener Zahlen. Dies ist ein Tutorial zu Optimierungsmethoden. Hier kann man nicht ohne Mathematik auskommen. Es ist okay, wenn du es komplett vergessen hast. Rückruf. Es wird keine formalen Beweise und komplexen Schlussfolgerungen geben, nur das notwendige Minimum für ein intuitives Verständnis. Zunächst ein kleiner Hintergrund darüber, wie dieser Algorithmus bei der Optimierung eines neuronalen Netzwerks hilfreich sein kann.

Vor sechs Monaten bat mich ein Freund zu zeigen, wie man in Python ein neuronales Netzwerk erstellt. Seine Firma produziert Instrumente für geophysikalische Messungen. Während des Bohrens messen mehrere verschiedene Sonden eine Reihe von Signalen, die den Parametern der Umgebung des Bohrlochs zugeordnet sind. In einigen komplexen Fällen können die Umgebungsparameter aus Signalen auch auf einem leistungsstarken Computer über einen langen Zeitraum genau berechnet werden, und es ist erforderlich, die Ergebnisse von Messungen vor Ort zu interpretieren. Es gab die Idee, mehrere hunderttausend Fälle in einem Cluster zu zählen und ein neuronales Netzwerk darauf zu trainieren. Da das neuronale Netzwerk sehr schnell ist, kann es verwendet werden, um Parameter zu bestimmen, die mit den gemessenen Signalen übereinstimmen, direkt während des Bohrvorgangs. Details finden Sie im Artikel:

D. Kushnir, N. Velker, A. Bondarenko, G. Dyatlov & Y. Dashevsky (2018, 29. Oktober). Echtzeitsimulation des Werkzeugs für den tiefen azimutalen Widerstand im 2D-Fehlermodell unter Verwendung neuronaler Netze (russisch). Gesellschaft der Erdölingenieure. doi: 10.2118 / 192573-RU

Eines Abends zeigte ich, wie Keras ein einfaches neuronales Netzwerk implementieren können, und ein Freund bei der Arbeit begann mit dem Training der gezählten Daten. Nach ein paar Tagen diskutierten wir das Ergebnis. Aus meiner Sicht sah er vielversprechend aus, aber ein Freund sagte, er brauche Berechnungen mit der Genauigkeit des Geräts. Und wenn sich herausstellte, dass der mittlere quadratische Fehler bei 1 lag, wurde 1e-3 benötigt. 3 Bestellungen weniger. Tausendmal.

Experimente mit neuronalen Netzwerkarchitekturen, Datennormalisierungs- und Optimierungsansätzen ergaben fast nichts. Ein paar Wochen später rief ein Freund an und sagte, er habe MatLab installiert und das Problem mit der Levenberg-Marquardt- Methode gelöst (im Folgenden werden wir LM nennen). Es wurde für eine lange Zeit (mehrere Tage) optimiert, es funktionierte nicht auf der GPU, aber das Ergebnis war das richtige. Es klang wie eine Herausforderung.

Eine schnelle Suche nach einem vorgefertigten LM-Optimierer für Keras oder TensorFlow ist fehlgeschlagen. Ich bin nur auf die Pyrenn-Bibliothek gestoßen, aber ihre Funktionalität schien mir schlecht. Ich habe beschlossen, es selbst umzusetzen. Auf den ersten Blick sah alles einfach aus, und zwei Abende hätten ausreichen sollen. Es dauerte länger. Es gab zwei Probleme:

1. TensorFlow. Eine Reihe von Artikeln, aber fast alle Ebenen "aber schreiben wir hallo Welt handgeschriebene Ziffernerkennung."
2. Mathe Ich habe viel vergessen, und die Autoren mathematischer Artikel interessieren sich überhaupt nicht für Leute wie mich: feste Formeln ohne Erklärung, "offensichtlich!" usw.

Infolgedessen schrieb er einen Artikel für diejenigen, die die Mathematik vergessen haben und TensorFlow etwas tiefer verstehen wollen, aber ohne Hardcore. Der Artikel enthält viel Text und wenig Code. Die entgegengesetzte Option, wenn es wenig Text und viel Code gibt, ist hier Jupyter Notebook Levenberg-Marquardt .

Lernen Sie die Rosenbrock-Funktion kennen

Wir werden Trainingsdaten mit der Rosenbrock-Funktion generieren, die häufig als Benchmark für Optimierungsalgorithmen verwendet wird:

$$ $$f (x, y) = (a-x) ^ 2 + b (y-x ^ 2) ^ 2$$

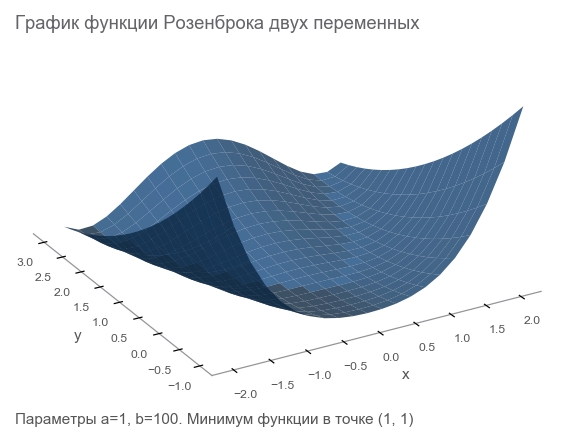
Warum ist sie gut?

• Schöner Zeitplan. Es heißt Rosenbrock-Tal und die unübersetzbare Rosenbrock-Bananenfunktion .
• Das globale Minimum befindet sich in einem langen, schmalen, parabolisch flachen Tal. Ein Tal zu finden ist trivial und ein globales Minimum ist schwierig.
• Es gibt eine mehrdimensionale Option. Es ist nicht so einfach, für viele Variablen eine gute Funktion zu entwickeln.

Wir beginnen mit dem Schreiben von Code, indem wir die für die weitere Arbeit erforderlichen Bibliotheken verbinden:

import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2 

Wir geben das Problem an

Da es sich um ein Messgerät handelt, verwenden wir die Analogie weiter. Unser Gerät in einer fiktiven Welt kann Koordinaten messen $$$(x, y)$ und Höhe $$$z$ . Physiker studierten die Welt und sagten: " Ja, das ist Rosenbrock! Wenn Sie die Koordinaten kennen, können Sie die Höhe genau berechnen, Sie müssen sie nicht messen. " Mit anderen Worten, Wissenschaftler gaben uns ein Modell $$$z = Rosenbrock (x, y, a, b)$ das hängt von den Parametern ab $$$(a, b)$ . Obwohl diese Parameter in einer fiktiven Welt konstant sind, sind sie unbekannt. Sie müssen gefunden werden.

Wir haben eine Reihe von Experimenten durchgeführt, die ergeben haben $$$m$ Punkte $$$(x_1, y_1, z_1), (x_2, y_2, z_2), ..., (x_m, y_m, z_m)$ ::

 # (2.5, 2.5) -   ,  ,     data_points = np.array([[x, y, rosenbrock(x, y, 2.5, 2.5)] for x in np.arange(-2, 2.1, 2) for y in np.arange(-2, 2.1, 2)]) m = data_points.shape[0] 

Die erste Möglichkeit zur Optimierung besteht darin, die Parameter zu erraten. Wir verwenden die Numpy-Bibliothek:

 x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2] #   =5  b=5? a_guess, b_guess = 5., 5. #  -hat   ,   , #   ,   ,   .   #     ^   - # .    hat. z_hat = rosenbrock(x, y, a_guess, b_guess) 

Wie kann man verstehen, wie falsch wir sind? Residuen zählen - Fehlergrößen. $$$m$ Punkte geben $$$m$ Residuen - Sie benötigen einen integralen Indikator. Wir quadrieren jeden Rest in einem Quadrat und berechnen den Durchschnitt:

$$ $$MSE (a, b) = \ frac {1} {m} \ sum_ {i = 1} ^ {m} (z_ {i} - \ widehat {z_ {i}}) ^ 2$$

Dieses Maß für die Nähe wird als mittlerer quadratischer Fehler bezeichnet (im Folgenden als mse bezeichnet ):

 # r - residuals () r = z - z_hat # mse loss = np.mean(r**2) print(loss) 

 [Out]: 3868.2291666666665 

Durch Minimierung von mse lösen wir das Problem der kleinsten Quadrate ( Minimierung nichtlinearer Quadrate ):

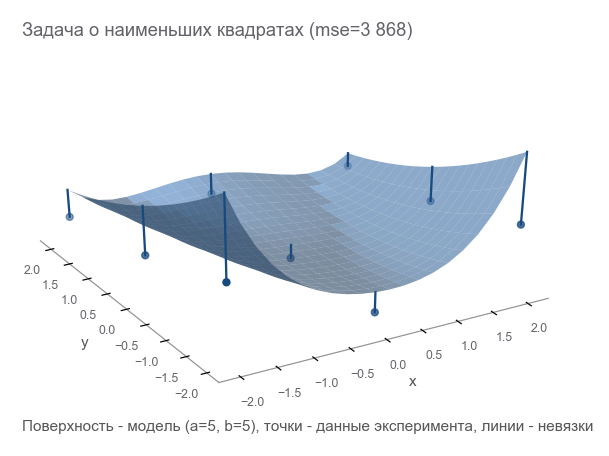
Es ist ersichtlich, dass die Parameter überhaupt nicht geraten haben.

Wir formulieren das Problem auf TensorFlow

Das Modell hat die Form $$$z = Rosenbrock (x, y, a, b)$ . Wir bringen es auf die Form $$$y = f (x, p)$ (Normalerweise schreibt Mathe $$$\ beta$ statt $$$p$ Programmierer verwenden jedoch keine Beta). Jetzt hat das Modell die Form $$$y = Rosenbrock (x, p)$ wo $$$y$ - Höhe $$$x$ Ist der Koordinatenvektor zweier Elemente (Komponente) und $$$p$ - Vektor der Parameter.

Programmierer betrachten Vektoren oft als eindimensionale Arrays. Das ist nicht ganz richtig. Ein Array von Zahlen ist ein Mittel zur Darstellung eines Vektors. Sie können einen Vektor als Array von Dimensionen darstellen $$$N$ zweidimensionales Array $$$1 \ mal N$ und sogar ein Array $$$N \ mal 1$ in Fällen, in denen die Tatsache, dass der Vektor ein Spaltenvektor ist (zum Beispiel um eine Matrix damit zu multiplizieren), wichtig ist:

$$ $$\ begin {bmatrix} x_1 \\\ vdots \\ x_N \ end {bmatrix}$$

TensorFlow verwendet das Konzept des Tensors . Ein Tensor kann wie ein Array eindimensional (zur Darstellung eines Vektors ), zweidimensional (für einen Matrix- oder Spaltenvektor ) und jede größere Dimension sein.

 #    ('placeholder' ,    #      ) x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m]) #   ('variable' ,    ) #     (5, 5) p = tf.Variable([5., 5.], dtype=tf.float64) #  y_hat = rosenbrock(x[:, 0], x[:, 1], p[0], p[1]) #  r = y - y_hat # mse (mean squared error) loss = tf.reduce_mean(r**2) 

Der TensorFlow-Code unterscheidet sich in seiner Form nicht vom Numpy-Code. Der Inhalt ist riesig. Numpy Code berechnet den mse- Wert . Der TensorFlow-Code führt überhaupt keine Berechnungen durch, sondern bildet ein Datenflussdiagramm , das mse berechnen kann . Ein sehr hirntoleranter Moment ist die Arbeit der Rosenbrock- Funktion. Wir verwenden es in beiden Fällen. Wenn wir jedoch die Numpy-Arrays übergeben, werden die Berechnungen gemäß der Formel ausgeführt und die Zahlen zurückgegeben. Wenn wir die Tensoren an TensorFlow übertragen, bildet dies einen Teilgraphen des Datenstroms und gibt seine Kante in Form eines Tensors zurück. Wunder des Polymorphismus, aber missbrauchen Sie sie nicht:

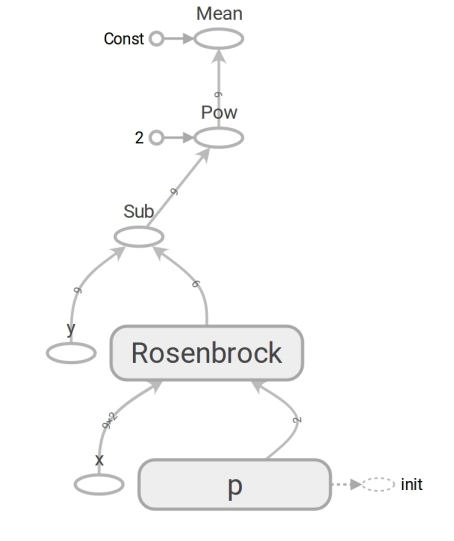
Dank des Vorhandenseins eines solchen Datenflussdiagramms kann insbesondere TensorFlow Ableitungen automatisch berechnen (unter Verwendung der automatischen Differenzierungstechnik im umgekehrten Modus ).

Ein Moment der Mathematik. Blöcke "für diejenigen, die vergessen haben" werden in einem Spoiler versteckt.

Wir haben ein Datenflussdiagramm erstellt. Lassen Sie uns die mse-Berechnung ausführen:

 #        #      placeholder (  ) feed_dict = {x: data_points[:,0:2], y: data_points[:,2]} #       TensorFlow session = tf.Session() #     session.run(tf.global_variables_initializer()) #   ()  loss (mse) current_loss = session.run(loss, feed_dict) print(current_loss) 

 [Out]: 3868.2291666666665 

Das Ergebnis ist das gleiche wie bei Numpy. Sie haben sich also nicht geirrt.

Beginnen Sie mit der Optimierung

Leider war es nicht möglich, die Parameter zu erraten. Aber dann haben wir:

1. Wir setzen das Optimalitätskriterium - den Minimalwert von mse.
2. Es wurden variable Parameter bestimmt: Vektor $$$p$ mit Komponenten $$$a$ , $$$b$ Rosenbrock funktioniert.
3. Wir haben noch nicht über Einschränkungen nachgedacht, aber sie sind nicht da.

Im letzten Schritt haben wir ein Datenflussdiagramm mit einem Tensor für endliche Verluste ( Verlustfunktion ) erstellt. Ziel der Optimierung ist es, den Wert des Parametervektors zu ermitteln $$$p$ bei dem der Wert der Verlustfunktion minimal ist. Wir hatten Glück, der Graph dieser Funktion ist sehr einfach (konkav und ohne lokale Minima):

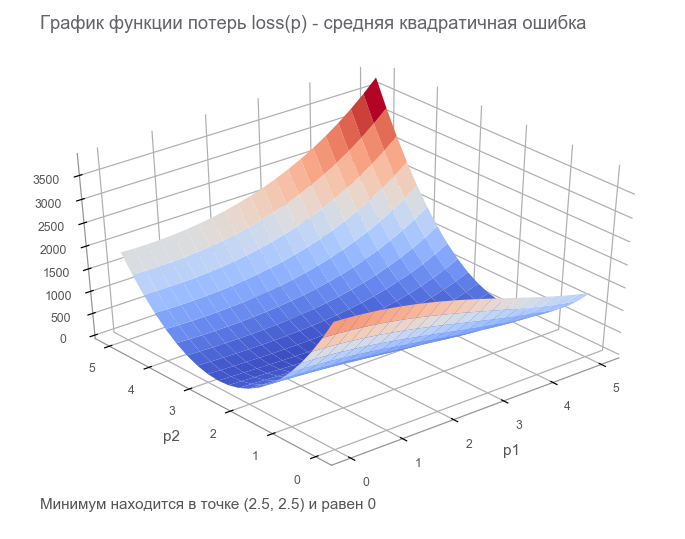
Erste Schritte mit der Optimierung. Zunächst schreiben wir einen verallgemeinerten Zyklus:

 # :   mse,   ,  #   mse,        placeholder def train(target_loss, max_steps, loss_tensor, train_step_op, inputs): step = 0 current_loss = session.run(loss_tensor, inputs) #           while current_loss > target_loss and step < max_steps: step += 1 #    1, 2, 4, 8, 16...  if math.log(step, 2).is_integer(): print(f'step: {step}, current loss: {current_loss}') #    session.run(train_step_op, inputs) current_loss = session.run(loss_tensor, inputs) print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') 

Wir optimieren nach der Methode des schnellsten Gradientenabstiegs (SGD)

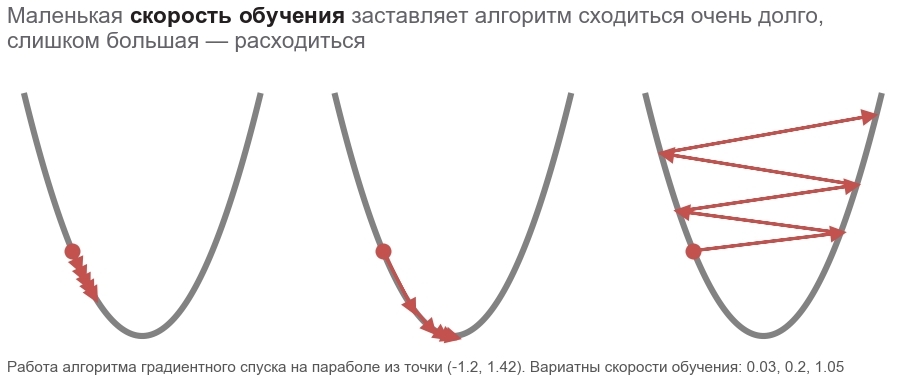
Die Aktionen dieser Methode können mit dem Fahren eines gewagten Skifahrers verglichen werden, der immer die Piste hinunterfährt (in der steilsten Richtung). In diesem Fall wird nur die Steigung am Standortpunkt berücksichtigt. Und wenn die Piste stark ist, fliegt der Skifahrer vor dem nächsten Wechsel eine lange Strecke. Mit einer schwachen Steigung bewegt es sich in kleinen Schritten. Vielleicht, wie man wegfliegt in einen Baum (Der Algorithmus divergiert ) und bleibt in einer Grube stecken ( lokales Minimum ).

Sie können wie folgt schreiben (ändern $$$\ boldsymbol {p}$ auf $$$\ boldsymbol {p} - ...$ ):

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - \ alpha [\ nabla_ {p} Verlust (\ boldsymbol {p})]$$

Fettig $$$\ boldsymbol {p}$ betont, dass dies der Punkt der tatsächlichen Position ist - der Wert des Parametervektors im aktuellen Schritt. Im ersten Schritt ist dies unsere Vermutung (5, 5). Die Formel enthält zwei interessante Punkte: $$$\ alpha$ - Lernrate ( Lernrate ), $$$\ nabla_ {p} Verlust$ - Gradient ( Gradient ) der Verlustfunktion durch den Parametervektor.

 #        grad = tf.gradients(loss, p)[0] #   learning_rate = 0.0005 #   ,     apply_gradients - #         opt = tf.train.GradientDescentOptimizer(learning_rate=1) #           sgd = opt.apply_gradients([(learning_rate*grad, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, sgd, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959] 

Es dauerte 582 Schritte:

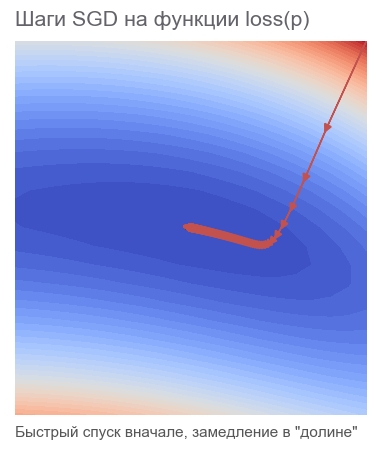
Wir optimieren nach der Adam-Methode

Wir werden nicht weiter auf Gradientenmethoden eingehen, aber es gibt viele Variationen. Sie können darüber im Artikel Methoden zur Optimierung neuronaler Netze lesen. In TensorFlow sind bereits viele Optimierer implementiert. Zum Beispiel Adam:

 #       , #      adm = tf.train.AdamOptimizer(15).minimize(loss) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, adm, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008] 

In 317 Schritten verwaltet. Viel schneller.

Wir optimieren nach Newtons Methode

Die Aktionen von Methoden zweiter Ordnung können mit dem Fahren eines rationalen Freeride-Snowboarders verglichen werden, der lange über den nächsten Punkt seiner Route nachdenkt und nicht nur die Steigung am Standort, sondern auch die Krümmung berücksichtigt.

Tatsächlich versuchen sowohl Gradientenabstiegsmethoden als auch Methoden zweiter Ordnung, die Funktion am aktuellen Punkt zu erraten (zu approximieren ). Gradientenmethoden konzentrieren sich nur auf die Steigung des Funktionsgraphen am Punkt - der ersten Ableitung. Methoden zweiter Ordnung berücksichtigen zusätzlich zur Vorspannung die Krümmung , die zweite Ableitung: "Wenn die Krümmung bestehen bleibt, wo wird dann das Minimum sein?" Wir rechnen und gehen dorthin:

Um eine solche Näherung zu konstruieren und den geschätzten Mindestpunkt zu berechnen, können Sie die Taylor-Reihe verwenden . Für den eindimensionalen Fall die Approximation durch ein Polynom zweiter Ordnung am Punkt $$$a$ sieht so aus:

$$ $$f (x) \ ungefähr f (a) + \ frac {f '(a) (x-a)} {1!} + \ frac {f' '(a) (x-a) ^ 2} {2!}$$

Das Minimum wird bei erreicht $$$x = a - \ frac {f '(a)} {f' '(a)}$ . Der mehrdimensionale Fall sieht ernster aus:

Approximation eines Polynoms zweiter Ordnung für eine Funktion eines Vektors durch einen Gradienten und eine hessische Matrix an einem Punkt $$$a$ sieht so aus:

$$ $$f (x) \ ungefähr f (a) + (xa) ^ \ intercal [\ nabla_ {x} f (a)] + \ frac {1} {2!} (xa) ^ \ intercal [\ boldsymbol {H. } f_ {x} (a)] (xa)$$

Das Minimum wird bei erreicht $$$x = a - [\ boldsymbol {H} f_ {x} (a)] ^ {- 1} [\ nabla_ {x} f (a)]$ . Die Form stimmt fast mit dem eindimensionalen Fall überein: Wir haben die erste Ableitung durch einen Gradienten ersetzt, die zweite durch eine hessische Matrix und eine Korrektur für die Arbeit mit Vektoren vorgenommen. Es ist unmöglich, einen Vektor durch eine Matrix zu teilen, daher wird eine Multiplikation mit der inversen Matrix verwendet. T bedeutet transponieren . Die Formel impliziert, dass ein Vektor standardmäßig eine Spalte ist. Transponieren verwandelt einen Spaltenvektor in einen Zeilenvektor . Bei der Implementierung in TensorFlow sollte dies berücksichtigt werden, jedoch in umgekehrter Richtung: Standardmäßig ist der Vektor eine Zeichenfolge (eindimensionaler Tensor). Nur für den Fall: Die Transposition ist keine Drehung um 90 Grad, sondern die Umwandlung von Zeilen in Spalten in derselben Reihenfolge.

Der Schritt der Newton-Methode hat also die folgende Form:

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {H} loss_ {p} (\ boldsymbol {p})] ^ {- 1} [\ nabla_ {p} loss (\ boldsymbol {p} )]$$

TensorFlow bietet alles, um diese Methode zu implementieren:

 #        hess = tf.hessians(loss, p)[0] #    - grad_col = tf.expand_dims(grad, -1) # ,      dp = tf.matmul(tf.linalg.inv(hess), grad_col) #  -  - dp = tf.squeeze(dp) #  p  dp    newton = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, newton, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5] 

Genug 6 Schritte:

Optimiert durch den Gauß-Newton-Algorithmus

Newtons Methode hat einen Nachteil - die hessische Matrix. Dank TensorFlow können wir es in einer Codezeile zählen. Johann Karl Friedrich Gauß erwähnte laut Wiki 1809 erstmals seine Methode. Die Berechnung der hessischen Matrix für mehrere Parameter für die Methode der kleinsten Quadrate kann dann viel Zeit in Anspruch nehmen. Nun können wir annehmen, dass der Gauß-Newton-Algorithmus die Approximation der Hessischen Matrix durch die Jacobi-Matrix verwendet , um die Berechnungen zu vereinfachen. Aus geschichtlicher Sicht ist dies jedoch nicht der Fall: Ludwig Otto Hesse (der die nach ihm benannte Matrix entwickelte) wurde 1811 geboren - zwei Jahre nach der ersten Erwähnung des Algorithmus. Und Carl Gustav Jacobi war 5 Jahre alt.

Der Gauß-Newton-Algorithmus funktioniert nicht mit der Verlustfunktion. Es funktioniert mit der Restfunktion $$$r (p)$ . Diese Funktion verwendet einen Eingabevektor von Parametern $$$p$ und gibt einen Residuenvektor zurück . In unserem Fall der Vektor $$$p$ besteht aus 2 Komponenten (Parameter $$$a$ und $$$b$ Rosenbrock-Funktionen) und der Restvektor aus $$$m$ Komponente (entsprechend der Anzahl der Experimente). Die Vektorfunktion des Vektorarguments wird erhalten. Seine Ableitung:

Um nicht in der Fülle der Zeichen verwirrt zu werden, nehmen wir das an $$$\ boldsymbol {J} _ {r}$ - Jacobi-Matrix der Restfunktionen am aktuellen Punkt $$$\ boldsymbol {p}$ . Dann kann der Gauß-Newton-Algorithmus wie folgt geschrieben werden:

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}] ^ {- 1} \ boldsymbol {J} _ {r } ^ \ intercal r (\ boldsymbol {p})$$

Die Aufzeichnung in der Form stimmt vollständig mit der Aufzeichnung der Newtonschen Methode überein. Nur anstelle der hessischen Matrix wird verwendet $$$\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}$ anstelle des Gradienten $$$\ boldsymbol {J} _ {r} ^ \ intercal r (\ boldsymbol {p})$ . Als nächstes werden wir sehen, warum eine solche Annäherung verwendet werden kann. Fahren wir in der Zwischenzeit mit der Implementierung auf TensorFlow fort:

 #  ,  TensorFlow     , #   ,        #  .  ,   : # 1)       tf.unstack(r) # 2)      tf.gradients(r_i, p) # 3)       tf.stack #      ,     #       j = tf.stack([tf.gradients(r_i, p)[0] for r_i in tf.unstack(r)]) jT = tf.transpose(j) #     - r_col = tf.expand_dims(r, -1) #      hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r_col) # ,      dp = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) #  -  - dp = tf.squeeze(dp) #  p  dp    ng = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, ng, feed_dict) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5] 

Genug 4 Schritte. Weniger als bei Newtons Methode.

Wie aus dem Code ersichtlich ist, wird die Verlustfunktion bei der Optimierung nicht nur zum Stoppen und Protokollieren von Kriterien verwendet. Woher weiß der Optimierungsalgorithmus, welche Funktion zu minimieren ist? Die Antwort ist überraschend: auf keinen Fall! Gauß-Newton minimiert nur den mittleren quadratischen Fehler .

Korrigieren Sie den mathematischen Teil des Artikels

Wir wiederholten alle Mathe, die wir brauchten. Lassen Sie es uns ein wenig beheben, um uns weiter nur auf die Programmierung und TensorFlow zu konzentrieren. Möglicherweise benötigen Sie einen Bleistift, um die Abfolge der mathematischen Aktionen zu verfolgen.

Es gibt ein Modell $$$y = f (x, p)$ wo $$$x$ - Vektor $$$p$ - Vektor der Dimensionsparameter $$$n$ und $$$y$ - Skalar. Aus den erhaltenen Experimenten $$$m$ Punkte $$$(x_ {1}, y_ {1}), ..., (x_ {m}, y_ {m})$ ( Datenpaare ). Die Vektorrestfunktion hängt nur vom Parametervektor ab: $$$r (p) = (r_ {1} (p), ... r_ {m} (p))$ wo $$$r_ {k} (p) = y_ {k} - \ widehat {y_ {k}} = y_ {k} - f (x_ {k}, p)$ . , $$$p$ , $$$x_{k}, y_{k}$ ? , $$$x_{k}, y_{k}$ , .

$$$p$ , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , $$$m$ . . :

$$ $$loss(p) = r_{1}^2(p) + \cdots + r_{m}^2(p) = \sum_{k=1}^{m} r_{k}^2(p)$$

$$$p$ $$$(p)$ .

, . — . — , $$$r^2$ $$$2r \frac{\partial r}{\partial p}$ . :

$$ $$\nabla_{p}loss = (\sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{1}}, \cdots, \sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{n}})$$

. :

$$ $$[\boldsymbol{H}loss_{p}]_{ij} = \frac{\partial^2 loss}{\partial p_{i} \partial p_{j}} = \sum_{k=1}^{m}(2\frac{\partial r_{k}}{\partial p_{i}}\frac{\partial r_{k}}{\partial p_{j}} + 2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}})$$

. , , $$${(uv)}'={u}'v+u{v}'$ .
Großartig! .

, , , — $$$2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$ . , , $$$r_{k}$ , . — . , ? -.

:

$$ $$\boldsymbol{J}_{r} = \begin{pmatrix} \frac{\partial r_{1}}{\partial p_{1}} & \cdots & \frac{\partial r_{1}}{\partial p_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_{m}}{\partial p_{1}} & \cdots & \frac{\partial p_{m}}{\partial p_{n}} \end{pmatrix}$$

, , . Beachten Sie Folgendes:

$$ $$2\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r} \approx \boldsymbol{H}loss_{p}$$

"" . ( ). , — $$$2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$ , .
( ):

$$ $$2\boldsymbol{J}_{r}^\intercal r = \nabla_{p}loss$$

, , - — , mse .

. , , . $$$m$ $$$(x_{1}, y_{1}), ..., (x_{m}, y_{m})$ , $$$y = rosenbrock(x, p)$ . $$$p$ , .

, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .

( multi-layer perceptron neural network mlp ). , , :

• ( starting values ) . Xavier'a, .
• ( overfitting ). — . , . — .
• ( scaling of the input ). , .

9 . 500:

 #    def get_random_rosenbrock_data_points(m): result = np.zeros((m, 3)) result[:, 0] = np.random.uniform(-2, 2, m) result[:, 1] = np.random.uniform(-2, 2, m) result[:, 2] = rosenbrock(result[:, 0], result[:, 1], 2.5, 2.5) return result m = 500 data_points = get_random_rosenbrock_data_points(m) # overfitting   ,      validation_data_points = get_random_rosenbrock_data_points(m) 

500 . — ( learner ), ( outcome measurement ) ( features ) .

( network diagram ). MatLab:

( input ). $$$W$ ( weights ) 2x10, $$$b$ ( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).

, , ( $$$tanh$ ):

$$ $$\begin{matrix} h_{1} = tanh(xW_{1} + b_{1})\\ \widehat{y} = h_{1}W_{2} + b_{2} \end{matrix}$$

:

$$ $$h_1 = tanh(\begin{bmatrix} x_1 & x_2 \end{bmatrix}\begin{bmatrix} w^{(1)}_{1,1} & \cdots& w^{(1)}_{1,10} \\ w^{(1)}_{2,1} &\cdots& w^{(1)}_{2,10} \end{bmatrix} + \begin{bmatrix} b^{(1)}_1 & \cdots & b^{(1)}_{10} \end{bmatrix}) \\ \widehat{y} = \begin{bmatrix}h^{(1)}_1 & \cdots & h^{(1)}_{10}\end{bmatrix} \begin{bmatrix} w^{(2)}_{1,1} \\ \vdots \\ w^{(2)}_{1,10} \\ \end{bmatrix} + b_2$$

. $$$W_{1}$ "" $$$h_{1}$ , - $$$W_{2}$ . 41 . , .

$$$m \times 2$ , . - $$$\widehat{y}$ von $$$m$ :

 #     10 "" n_hidden = 10 #      Xavier'a initializer = tf.contrib.layers.xavier_initializer() #    x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m, 1]) #         W1 = tf.Variable(initializer([2, n_hidden], dtype=tf.float64)) b1 = tf.Variable(initializer([1, n_hidden], dtype=tf.float64)) #   ,  tanh   h1 = tf.nn.tanh(tf.matmul(x, W1) + b1) #        W2 = tf.Variable(initializer([n_hidden, 1], dtype=tf.float64)) b2 = tf.Variable(initializer([1], dtype=tf.float64)) #   y_hat = tf.matmul(h1, W2) + b2 #  r = y - y_hat #   mse     loss = tf.reduce_mean(tf.square(r)) #      placeholder feed_dict = {x: data_points[:,0:2], y: data_points[:,2:3]} validation_feed_dict = {x: validation_data_points[:,0:2], y: validation_data_points[:,2:3]} 

Adam

Adam $$$rosenbrock$ . mse :

 #    adm = tf.train.AdamOptimizer(1e-2).minimize(loss) session.run(tf.global_variables_initializer()) #   ,    40000  train(1e-10, 40000, loss, adm, feed_dict) print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict))) 

 [Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866 

. : , , .

$$$rosenbrock$ 2 . :

• . 9 , 500. .
• . - $$$p$ , .

:

 #      y   x def jacobian(y, x): loop_vars = [ tf.constant(0, tf.int32), tf.TensorArray(tf.float64, size=m), ] #  -   #      _, jacobian = tf.while_loop( lambda i, _: i < m, #           #   (-),   x     lambda i, res: (i+1, res.write(i, tf.reshape(tf.gradients(y[i], x), (-1,)))), loop_vars) #       return jacobian.stack() #       r_flat = tf.squeeze(r) #        #       parms = [W1, b1, W2, b2] parms_sizes = [tf.size(p) for p in parms] j = tf.concat([jacobian(r_flat, p) for p in parms], 1) jT = tf.transpose(j) #           hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r) 

$$$\boldsymbol{J}r_{p}$ . , 4 $$$W_1, b_1, W_2, b_2$ . 4 $$$\boldsymbol{J}r_{W_1}, \boldsymbol{J}r_{b_1}, \boldsymbol{J}r_{W_2}, \boldsymbol{J}r_{b_2}$ tf.concat .

. tf.while_loop , $$$r_i$ , , stack .

$$$r_i$ $$$W_1$ : $$$\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} \\ \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$ . tf.reshape (-1,) $$$\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} & \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$ .

. - . — TensorFlow . — - - $$$W_1, b_1, W_2, b_2$ . -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .

-

hess_approx grad_approx -. $$$rosenbrock$ , . :

1. : $$$\Delta \boldsymbol{p} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} & \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} & \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} & \Delta b_2\end{bmatrix}$
2. :
   $$$\Delta W_{1} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$ , $$$\Delta b_{1} = \begin{bmatrix} \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} \end{bmatrix}$ , $$$\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} \end{bmatrix}$ , $$$\Delta b_{2} = \begin{bmatrix} \Delta b_2\end{bmatrix}$ .
3. , :
   $$$\Delta W_{1} = \begin{bmatrix} \Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{1,10} \\ \Delta w^{(1)}_{2,1} &\cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$ , $$$\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} \\ \vdots \\ \Delta w^{(2)}_{1,10} \\ \end{bmatrix}$
4. .

 # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       gn = opt.apply_gradients(zip(dps, parms)) #   session.run(tf.global_variables_initializer()) train(1e-10, 100, loss, gn, feed_dict) 

 [Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible. 

- . , . - , .

, .

-

. Matlab trainlm . . MathWorks.

- : $$$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$ . - :

$$ $$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}+\mu \boldsymbol{I}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$$

$$$\ mu$ $$$I$ $$$n$ ( ). $$$\ mu$ , -. , . , LM -.

:

 mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64) # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx + tf.multiply(mu, I)), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       lm = opt.apply_gradients(zip(dps, parms)) 

$$$\ mu$ ? LM - . , . , $$$\ mu$ , . — , mse . , :

 #       store = [tf.Variable(tf.zeros(p.shape, dtype=tf.float64)) for p in parms] #  TensorFlow       save_parms = [tf.assign(s, p) for s, p in zip(store, parms)] restore_parms = [tf.assign(p, s) for s, p in zip(store, parms)] #   mu    3. feed_dict[mu] = np.array([3.]) step = 0 session.run(tf.global_variables_initializer()) #    mse current_loss = session.run(loss, feed_dict) #    100   while current_loss > 1e-10 and step < 100: step += 1 #  1, 2, 4...   if math.log(step, 2).is_integer(): print(f'step: {step}, mu: {feed_dict[mu][0]} current loss: {current_loss}') #    session.run(save_parms) # ,     mse while True: #    session.run(lm, feed_dict) new_loss = session.run(loss, feed_dict) if new_loss > current_loss: #  -  mu  10     feed_dict[mu] *= 10 session.run(restore_parms) else: #  -  mu  10     feed_dict[mu] /= 10 current_loss = new_loss break print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict))) 

 [Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034 

100 LM mse 10 , 40 .

. , . , rosenbrock_train.py .

2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .

:

$$ $$f(\boldsymbol{x}) = \sum_{i=1}^{N-1}\left [ 100(x_{i+1} - x_{i}^2)^2 + (1-x_{i})^2 \right ], \boldsymbol{x}=[x_1 \cdots x_{N}]\in \mathbb{R}^N$$

rosenbrock_train.py get_rand_rosenbrock_points .

-

- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :

1. 10 000 6D .
2. 3 12, 10, 8 (311 ).
3. .
4. 3.5 .

. - 2 . LM . 20 .

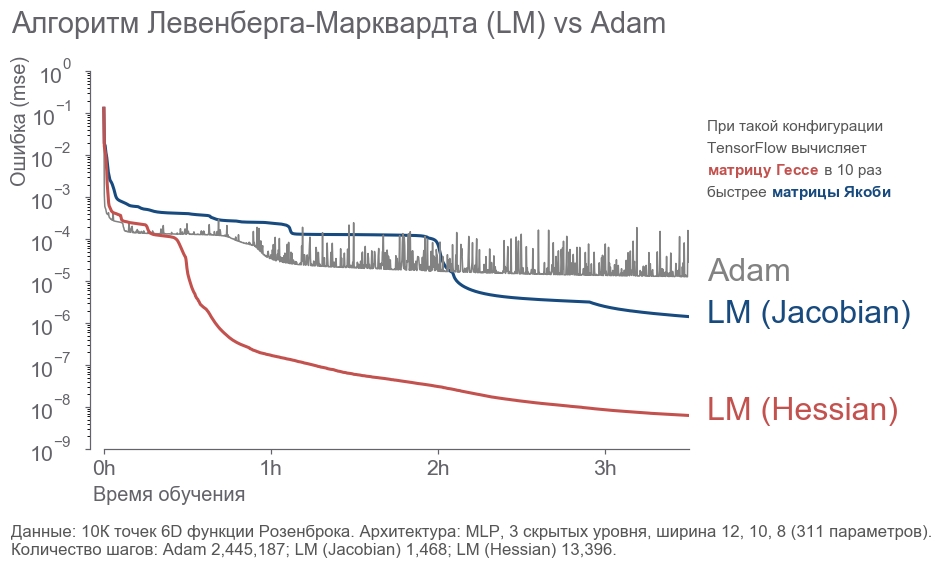
rosenbrock_train.py . . , .

Fazit

, . " ", , . , . , 273 . - , .

, :

1. .
2. ( ) -:
   [1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
   [2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.

, - . , . "".