Interpretieren von Modellvorhersagen in SHAP

Eine der wichtigsten Aufgaben auf dem Gebiet der Datenwissenschaft ist nicht nur die Konstruktion eines Modells, das qualitativ hochwertige Vorhersagen treffen kann, sondern auch die Fähigkeit, solche Vorhersagen zu interpretieren.

Wenn wir nicht nur wissen, dass der Kunde dazu neigt, ein Produkt zu kaufen, sondern auch verstehen, was seinen Kauf beeinflusst, können wir in Zukunft eine Unternehmensstrategie entwickeln, die auf die Verbesserung der Vertriebseffizienz abzielt.

Oder das Modell sagte voraus, dass der Patient bald krank werden würde. Die Genauigkeit solcher Vorhersagen ist nicht sehr hoch, weil Dem Modell sind viele Faktoren verborgen, aber eine Erklärung der Gründe, warum das Modell eine solche Vorhersage getroffen hat, kann dem Arzt helfen, auf neue Symptome zu achten. Somit ist es möglich, die Anwendungsgrenzen des Modells zu erweitern, wenn seine Genauigkeit an sich nicht zu hoch ist.

In diesem Beitrag möchte ich über die SHAP- Technik sprechen, mit der Sie unter die Haube einer Vielzahl von Modellen schauen können.

Wenn es bei linearen Modellen immer weniger klar ist, je größer der Absolutwert des Koeffizienten unter dem Prädiktor ist, desto wichtiger ist dieser Prädiktor, dann ist es viel schwieriger, die Bedeutung von Merkmalen derselben Gradientenverstärkung zu erklären.

Warum war eine solche Bibliothek nötig?

Im sklearn-Stack, in den xgboost, lightGBM-Paketen, gab es integrierte Methoden zur Bewertung der Wichtigkeit von Merkmalen (Merkmalsbedeutung) für "Holzmodelle":

1. Gewinn
   Diese Kennzahl zeigt den relativen Beitrag jedes Merkmals zum Modell. Zur Berechnung gehen wir jeden Baum durch, schauen uns jeden Baumknoten an, dessen Merkmal zur Partition des Knotens führt und wie stark die Modellunsicherheit gemäß der Metrik abnimmt (Gini-Verunreinigung, Informationsgewinn).
   Für jedes Merkmal wird sein Beitrag über alle Bäume zusammengefasst.
   
2. Abdecken
   Zeigt die Anzahl der Beobachtungen für jedes Merkmal an. Zum Beispiel haben Sie 4 Funktionen, 3 Bäume. Angenommen, Merkmal 1 an den Knoten des Baums enthält 10, 5 und 2 Beobachtungen in den Bäumen 1, 2 und 3. Dann ist für dieses Merkmal die Wichtigkeit 17 (10 + 5 + 2).
   
3. Frequenz
   Es wird angezeigt, wie oft dieses Feature in den Knoten des Baums gefunden wird, dh, die Gesamtzahl der Baumaufteilungen in Knoten für jedes Feature in jedem Baum wird berücksichtigt.
   

Das Hauptproblem bei all diesen Ansätzen besteht darin, dass nicht klar ist, wie genau sich dieses Merkmal auf die Modellvorhersage auswirkt. Zum Beispiel haben wir erfahren, dass die Höhe des Einkommens wichtig ist, um die Zahlungsfähigkeit eines Bankkunden zur Rückzahlung eines Kredits zu beurteilen. Aber wie genau? Wie viel höhere Einnahmen beeinflussen Modellvorhersagen?

Natürlich können wir verschiedene Vorhersagen treffen, indem wir das Einkommensniveau ändern. Aber was tun mit anderen Funktionen? Schließlich befinden wir uns in einer Situation, in der wir den Einfluss des Einkommens unabhängig von anderen Merkmalen mit ihrem Durchschnittswert verstehen müssen.

Es gibt eine Art durchschnittlicher Bankkunde "im luftleeren Raum". Wie werden sich Modellvorhersagen mit Einkommensänderungen ändern?

Hier kommt die SHAP- Bibliothek zur Rettung.

Wir berechnen die Wichtigkeit von Features mit SHAP

In der SHAP- Bibliothek werden zur Beurteilung der Wichtigkeit von Merkmalen Shapley-Werte berechnet (mit dem Namen eines amerikanischen Mathematikers und die Bibliothek wird benannt).

Um die Wichtigkeit eines Merkmals zu bewerten, werden die Modellvorhersagen mit und ohne dieses Merkmal ausgewertet.

Ein bisschen Vorgeschichte

Shapleys Bedeutungen stammen aus der Spieltheorie.

Stellen Sie sich das Szenario vor: Eine Gruppe von Personen spielt Karten. Wie verteilt man den Preisfonds entsprechend ihrem Beitrag auf sie?

Es werden eine Reihe von Annahmen getroffen:

• Die Höhe der Belohnung für jeden Spieler entspricht dem Gesamtpreispool
• Wenn zwei Spieler den gleichen Beitrag zum Spiel leisten, erhalten sie die gleiche Belohnung.
• Wenn ein Spieler keinen Beitrag geleistet hat, erhält er keine Belohnung.
• Wenn ein Spieler zwei Spiele verbracht hat, besteht seine Gesamtbelohnung aus der Anzahl der Belohnungen für jedes der Spiele

Wir präsentieren die Merkmale des Modells als Spieler und den Preispool als endgültige Vorhersage des Modells.

Schauen wir uns ein Beispiel an.

Die Formel zur Berechnung des Shapley-Werts für das i-te Merkmal:

$$$$ display $$ \ begin {Gleichung *} \ phi_ {i} (p) = \ sum_ {S \ subseteq N / \ {i \}} \ frac {| S |! (n - | S | -1) !} {n!} (p (S \ cup \ {i \}) - p (S)) \ end {Gleichung *} $$ display $$

Hier:

$$$p (S \ cup \ {i \})$ Ist eine Vorhersage eines Modells mit dem i-ten Merkmal,
$$$p (S)$- Dies ist eine Vorhersage des Modells ohne das i-te Merkmal.
$$$n$- Anzahl der Funktionen,
$$$S$- ein beliebiger Satz von Merkmalen ohne das i-te Merkmal

Der Shapley-Wert für das i-te Merkmal wird für jede Datenstichprobe (zum Beispiel für jeden Client in der Stichprobe) für alle möglichen Kombinationen von Merkmalen (einschließlich des Fehlens aller Merkmale) berechnet, dann werden die erhaltenen Werte modulo summiert und die endgültige Wichtigkeit des i-ten Merkmals wird erhalten.

Diese Berechnungen sind extrem teuer, daher werden unter der Haube verschiedene Algorithmen zur Optimierung von Berechnungen verwendet. Weitere Einzelheiten finden Sie unter dem obigen Link auf dem Github.

Nehmen Sie das Vanille-Beispiel aus der xgboost-Dokumentation .



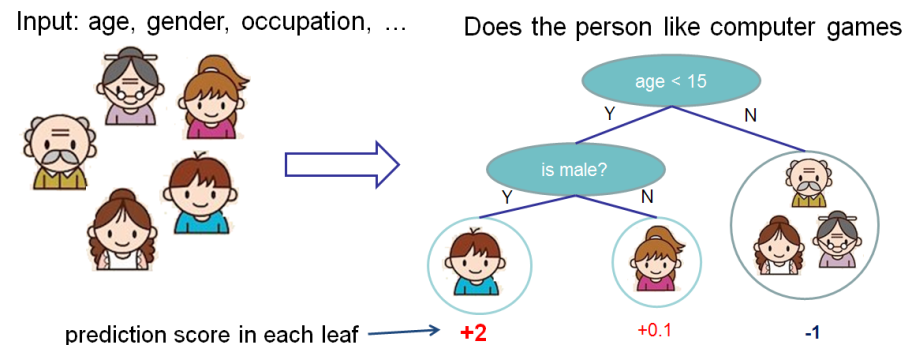
Wir möchten die Bedeutung von Funktionen für die Vorhersage bewerten, ob eine Person Computerspiele mag.

In diesem Beispiel haben wir der Einfachheit halber zwei Merkmale: Alter (Alter) und Geschlecht (Geschlecht). Geschlecht (Geschlecht) nimmt die Werte 0 und 1 an.

Nehmen Sie Bobby (den kleinen Jungen am äußersten linken Knoten des Baums) und berechnen Sie den Wert von Shapley für das Merkmalalter (Alter).

Wir haben zwei Sätze von S-Merkmalen:

$$$\ {\}$ - keine Funktionen
$$$\ {gender \}$ - Es gibt nur ein Merkmal Geschlecht.

Die Situation, wenn keine Feature-Werte vorhanden sind

Verschiedene Modelle funktionieren unterschiedlich in Situationen, in denen keine Merkmale für die Datenstichprobe vorhanden sind, dh für alle Merkmale sind die Werte NULL.

In diesem Fall wird berücksichtigt, dass das Modell die Vorhersagen über die Äste mittelt, dh die Vorhersage ohne Merkmale ist $$$[(2 + 0,1) / 2 + (-1)] / 2 = 0,025$.

Wenn wir das Wissen über das Alter hinzufügen, wird die Vorhersage des Modells sein $$$(2 + 0,1) / 2 = 1,05$.

Der Wert von Shapley für den Fall fehlender Funktionen:

$$

$$\ frac {| S |! (n - | S | -1)!} {n!} (p (S \ cup \ {i \}) - p (S)) = \ frac {1 (2-0 -1)!} {2!} (1,025) = 0,5125$$

Die Situation, wenn wir das Geschlecht kennen

Für Bobby für $$${gender}$Vorhersage ohne Merkmale Alter, nur mit Merkmalen Geschlecht ist gleich $$$[(2 + 0,1) / 2 + (-1)] / 2 = 0,025$. Wenn wir das Alter kennen, ist die Vorhersage der Baum ganz links, dh 2.

Infolgedessen ist der Wert von Shapley für diesen Fall:

$$$$ display $$ \ begin {Gleichung *} \ frac {| S |! (n - | S | -1)!} {n!} (p (S \ cup \ {i \}) - p (S) ) = \ frac {1 (2-1-1)!} {2!} (1.975) = 0.9875 \ end {Gleichung *} $$ display $$

Fassen Sie zusammen

Der Gesamtwert von Shapley für Merkmale Alter (Alter):

$$$$ Anzeige $$ \ begin {Gleichung *} \ phi_ {Age Bobby} = 0,9875 + 0,5125 = 1,5 \ Ende {Gleichung *} $$ Anzeige $$

Ein echtes Geschäftsbeispiel

Die SHAP-Bibliothek verfügt über eine umfangreiche Visualisierungsfunktionalität, mit deren Hilfe das Modell sowohl für das Unternehmen als auch für den Analysten selbst einfach und einfach erklärt werden kann, um die Angemessenheit des Modells zu bewerten.

Bei einem der Projekte habe ich den Abfluss von Mitarbeitern aus dem Unternehmen analysiert. Als Modell wurde xgboost verwendet.

Code in Python:

import shap shap_test = shap.TreeExplainer(best_model).shap_values(df) shap.summary_plot(shap_test, df, max_display=25, auto_size_plot=True) 

Das resultierende Diagramm der Wichtigkeit von Merkmalen:



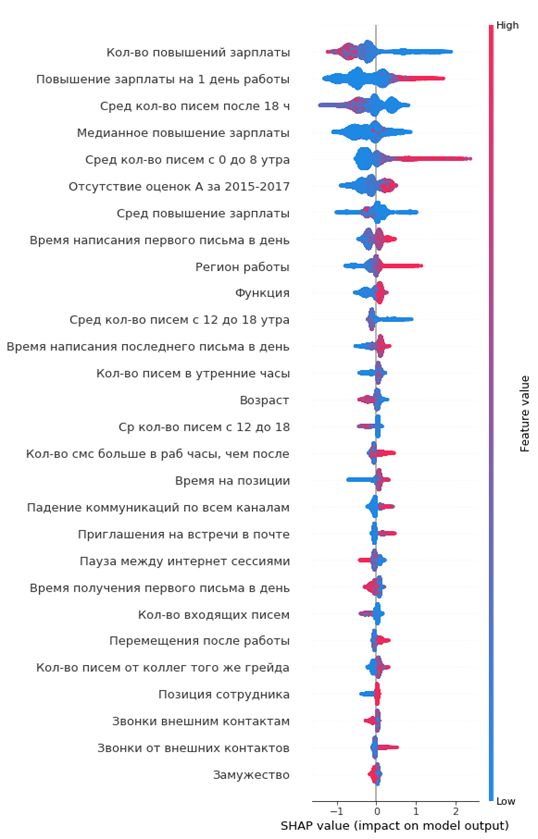
Wie man es liest:

• Die Werte links von der vertikalen Mittellinie sind die negative Klasse (0), rechts - positiv (1)
• Je dicker die Linie in der Grafik ist, desto mehr solche Beobachtungspunkte
• Je roter die Punkte im Diagramm sind, desto höher ist der Wert der darin enthaltenen Features

Aus der Grafik können Sie interessante Schlussfolgerungen ziehen und deren Angemessenheit überprüfen:

• Je niedriger die Gehaltserhöhung des Arbeitnehmers ist, desto höher ist die Wahrscheinlichkeit seiner Abreise
• Es gibt Regionen von Büros, in denen der Abfluss höher ist
• Je jünger der Arbeitnehmer ist, desto höher ist die Wahrscheinlichkeit seiner Abreise
• ...

Sie können sich sofort ein Porträt der scheidenden Mitarbeiterin machen: Sie hat sein Gehalt nicht erhöht, er war jung genug, ledig, lange Zeit auf einer Position, es gab keine Notenerhöhungen, es gab keine hohen Jahresbewertungen, er begann wenig mit Kollegen zu kommunizieren.

Einfach und bequem!

Sie können die Vorhersage für einen bestimmten Mitarbeiter erklären:



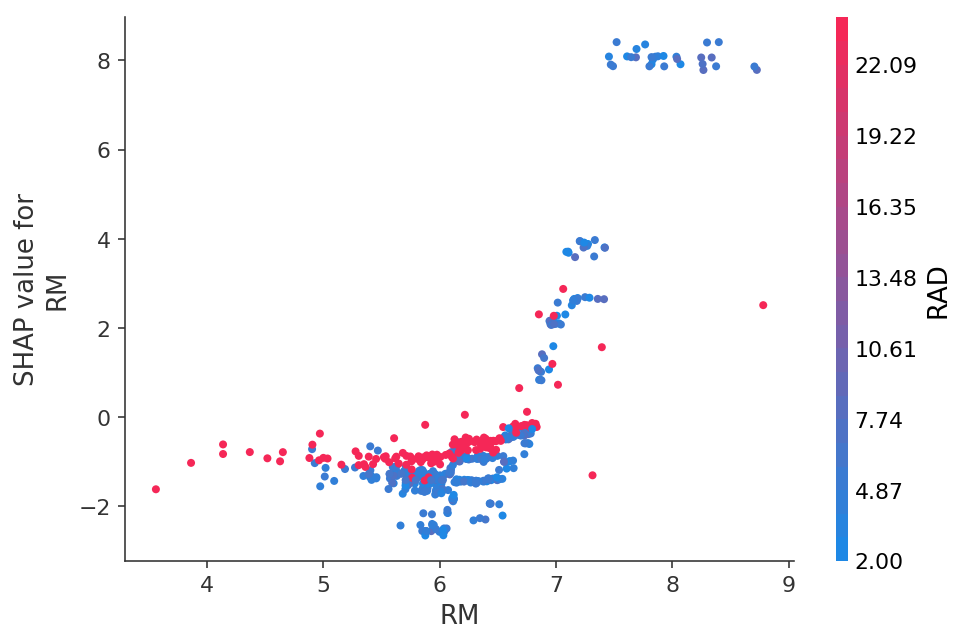
Oder sehen Sie die Abhängigkeit von Vorhersagen von einem bestimmten Merkmal in Form eines 2D-Diagramms:



Sie können sogar die Vorhersagen neuronaler Netze in Bildern visualisieren:

Fazit

Ich selbst habe vor ungefähr sechs Monaten etwas über SHAP-Werte gelernt, und dies hat andere Methoden zur Bewertung der Bedeutung von Merkmalen vollständig ersetzt.

Die Hauptvorteile:

• bequeme Visualisierung und Interpretation
• ehrliche Berechnung der Wichtigkeit von Merkmalen
• Die Möglichkeit, Funktionen für eine bestimmte Teilstichprobe von Daten auszuwerten (z. B. wie sich unsere Kunden von anderen Kunden in der Stichprobe unterscheiden), wird durch einen einfachen Filter des Datensatzes in Pandas und dessen Analyse in Form, buchstäblich ein paar Codezeilen, erreicht