🗒️ 🛥️ ✔️ Wir approximieren die Funktion mit einem neuronalen Netzwerk 👩‍🎓 🎤 🤴

Um Bibliotheken für die Arbeit mit neuronalen Netzen zu entwickeln, werden wir das Problem der Approximation der Funktion eines einzelnen Arguments unter Verwendung neuronaler Netzwerkalgorithmen für Training und Vorhersage lösen.

Eintrag

Es sei eine Funktion f gegeben: [x0, x1] -> R.

Wir approximieren die gegebene Funktion f durch die Formel

P(x) = SUM W[i]*E(x,M[i])

i = 1..n
M [i] von R.
W [i] von R.
E (x, M) = {0 für x <M; 1/2 mit x = M; 1, für x> M.

Offensichtlich gibt es bei einer gleichmäßigen Verteilung der Werte von M [i] im Intervall (x0, x1) solche Größen W [i], für die die Formel P (x) die Funktion f (x) am besten approximiert. Darüber hinaus können wir für gegebene Werte von M [i], die im Intervall (x0, x1) definiert und in aufsteigender Reihenfolge geordnet sind, einen sequentiellen Algorithmus zur Berechnung der Größen W [i] für die Formel P (x) beschreiben.

Und hier ist das neuronale Netzwerk

Wir transformieren die Formel P (x) = SUMME W [i] * E (x, M [i]) in ein neuronales Netzwerkmodell mit einem Eingangsneuron, einem Ausgangsneuron und n Neuronen mit versteckter Schicht

 P(x) = SUM W[i]*S(K[i]*x + B[i]) + C

Variable x - Eingangsschicht, die aus einem Neuron besteht
{K, B} - Parameter der "versteckten" Schicht, bestehend aus n Neuronen und Aktivierungsfunktion - Sigmoid
{W, C} - Parameter der "Ausgabeschicht", bestehend aus einem Neuron, das die gewichtete Summe seiner Eingaben berechnet.
S ist ein Sigmoid,

dabei

Anfangsparameter der "versteckten" Schicht K [i] = 1
Die Anfangsparameter der "versteckten" Schicht B [i] sind gleichmäßig auf das Segment verteilt (-x1, -x0).

Alle Parameter des neuronalen Netzwerks K, B, W und C werden durch Trainieren des neuronalen Netzwerks an Abtastwerten (x, y) der Werte der Funktion f bestimmt.

Sigmoid

Sigmoid ist eine glatte monoton ansteigende nichtlineare Funktion

S (x) = 1 / (1 + exp (-x)).

Das Programm

Wir verwenden das Tensorflow-Paket, um unser neuronales Netzwerk zu beschreiben.

 #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost)

Schulung

 init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values })

Volltext

 import math import numpy as np import tensorflow as tf import matplotlib.pyplot as plt x0, x1 = 10, 20 #    test_data_size = 2000 #      iterations = 20000 #    learn_rate = 0.01 #   hiddenSize = 10 #    #     def generate_test_values(): train_x = [] train_y = [] for _ in range(test_data_size): x = x0+(x1-x0)*np.random.rand() y = math.sin(x) #   train_x.append([x]) train_y.append([y]) return np.array(train_x), np.array(train_y) #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) if(_ % 1000 == 999): print("cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values }))) train_dataset, train_values = generate_test_values() train_values1 = session.run(model, feed_dict={ x: train_dataset, }) plt.plot(train_dataset, train_values, "bo", train_dataset, train_values1, "ro") plt.show() with tf.variable_scope("hidden", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("hidden:") print("kernel=", w.eval()) print("bias = ", b.eval()) with tf.variable_scope("output", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("output:") print("kernel=", w.eval()) print("bias = ", b.eval())

Das ist passiert

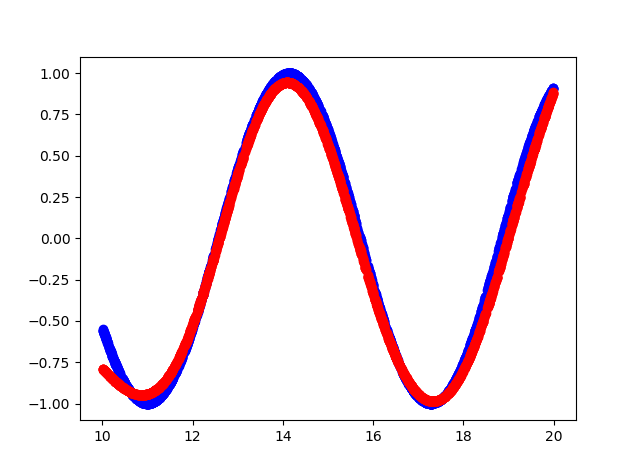
Blau ist die ursprüngliche Funktion.
Rote Farbe - Annäherung an die Funktion

Konsolenausgabe

 cost = 0.15786637365818024 cost = 0.10963975638151169 cost = 0.08536215126514435 cost = 0.06145831197500229 cost = 0.04406769573688507 cost = 0.03488277271389961 cost = 0.026663536205887794 cost = 0.021445846185088158 cost = 0.016708852723240852 cost = 0.012960446067154408 cost = 0.010525770485401154 cost = 0.008495906367897987 cost = 0.0067353141494095325 cost = 0.0057082874700427055 cost = 0.004624188877642155 cost = 0.004093789495527744 cost = 0.0038146725855767727 cost = 0.018593043088912964 cost = 0.010414039716124535 cost = 0.004842184949666262 hidden: kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508 0.87283015 1.0875995 0.9677301 0.6194152 ]] bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006 -13.379829 -20.508204 -14.923473 -19.354435] output: kernel= [[ 2.0069902 ] [-1.0321712 ] [-0.8878887 ] [-2.0531905 ] [ 1.4293027 ] [ 2.1250408 ] [-1.578137 ] [ 4.141281 ] [-2.1264815 ] [-0.60681605]] bias = [-0.2812019]

Quellcode

https://github.com/dprotopopov/nnfunc

Wir approximieren die Funktion mit einem neuronalen Netzwerk