Ich präsentiere Ihnen die Übersetzung eines Kapitels aus dem Buch Hands-On Data Science mit Anaconda
"Predictive Data Analytics - Modellierung und Validierung"
Unser Hauptziel bei der Durchführung verschiedener Datenanalysen ist die Suche nach Mustern, um vorherzusagen, was in Zukunft passieren wird. Für die Börse führen Forscher und Experten verschiedene Tests durch, um die Marktmechanismen zu verstehen. In diesem Fall können Sie viele Fragen stellen. Wie wird der Marktindex in den nächsten fünf Jahren sein? Was ist die nächste Preisspanne für IBM? Wird die Marktvolatilität in Zukunft zunehmen oder abnehmen? Was könnte der Effekt sein, wenn Regierungen ihre Steuerpolitik ändern? Was sind die potenziellen Gewinne und Verluste, wenn ein Land einen Handelskrieg mit einem anderen beginnt? Wie können wir das Verbraucherverhalten vorhersagen, indem wir einige verwandte Variablen analysieren? Können wir die Wahrscheinlichkeit eines erfolgreichen Abschlusses eines Doktoranden vorhersagen? Können wir einen Zusammenhang zwischen dem spezifischen Verhalten einer bestimmten Krankheit finden?
Daher werden wir die folgenden Themen betrachten:
- Grundlegendes zur prädiktiven Datenanalyse
- Nützliche Datensätze
- Vorhersage zukünftiger Ereignisse
- Modellauswahl
- Granger-Kausaltest
Grundlegendes zur prädiktiven Datenanalyse
Menschen haben möglicherweise viele Fragen zu zukünftigen Ereignissen.
- Wenn ein Investor die zukünftige Bewegung der Aktienkurse vorhersagen kann, kann er einen großen Gewinn erzielen.
- Unternehmen könnten, wenn sie den Trend ihrer Produkte vorhersagen könnten, ihren Aktienkurs und ihren Marktanteil erhöhen.
- Wenn die Regierungen die Auswirkungen einer alternden Bevölkerung auf Gesellschaft und Wirtschaft vorhersagen könnten, hätten sie mehr Anreize, eine bessere Politik im Hinblick auf den Staatshaushalt und andere relevante strategische Entscheidungen zu entwickeln.
- Wenn die Universitäten die Marktnachfrage in Bezug auf Qualität und Fähigkeiten ihrer Absolventen gut verstehen könnten, könnten sie eine Reihe besserer Programme entwickeln oder neue Programme starten, um den zukünftigen Bedarf an Arbeitskräften zu decken.
Für eine bessere Prognose sollten Forscher viele Fragen berücksichtigen. Sind die Beispieldaten beispielsweise zu klein? Wie entferne ich fehlende Variablen? Ist dieser Datensatz in Bezug auf Datenerfassungsverfahren voreingenommen? Wie stehen wir zu Extremen oder Emissionen? Was ist Saisonalität und wie gehen wir damit um? Welche Modelle sollen wir verwenden? In diesem Kapitel werden einige dieser Probleme behandelt. Beginnen wir mit einem nützlichen Datensatz.
Nützliche Datensätze
Eine der besten Datenquellen ist das
UCI Machine Learning Repository . Nach dem Besuch der Website sehen wir die folgende Liste:

Wenn Sie beispielsweise den ersten Datensatz (Abalone) auswählen, wird Folgendes angezeigt. Um Platz zu sparen, wird nur die Oberseite angezeigt:

Von hier aus können Benutzer den Datensatz herunterladen und Variablendefinitionen finden. Der folgende Code kann zum Laden eines Datensatzes verwendet werden:
dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets)
Die entsprechende Ausgabe wird hier angezeigt:

Aus der vorherigen Schlussfolgerung wissen wir, dass der Datensatz 427 Beobachtungen (Datensätze) enthält. Für jede von ihnen haben wir 7 verwandte Funktionen, wie
Name, Datentypen, Standardaufgabe, Attributtypen, N_Instanzen (Anzahl der Instanzen),
N_Attribute (Anzahl der Attribute) und
Jahr . Eine Variable namens
Default_Task kann als Hauptverwendung jedes Datensatzes interpretiert werden. Beispielsweise kann ein erster Datensatz namens
Abalone zur
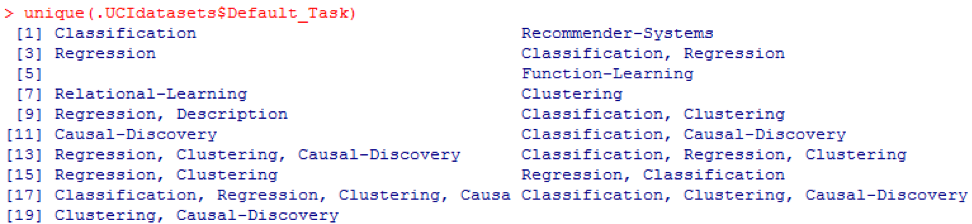
Klassifizierung verwendet werden . Mit der Funktion
unique () können Sie nach allen hier gezeigten möglichen
Default_Task suchen:
R-Paket AppliedPredictiveModeling
Dieses Paket enthält viele nützliche Datensätze, die für dieses und andere Kapitel verwendet werden können. Der einfachste Weg, diese Datensätze zu finden, ist die hier gezeigte Funktion
help () :
library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling)
Hier zeigen wir einige Beispiele zum Laden dieser Datensätze. Um einen Datensatz zu laden, verwenden wir die Funktion
data () . Für den ersten Datensatz namens
Abalone haben wir den folgenden Code:
library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone)
Die Ausgabe ist wie folgt:

Manchmal enthält ein großer Datensatz mehrere Unterdatensätze:
library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol")
[1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY"
Um jeden Datensatz zu laden, können wir die Funktionen
dim () ,
head () ,
tail () und
summary () verwenden .
Zeitreihenanalyse
Zeitreihen können als eine Reihe von Werten definiert werden, die zu aufeinanderfolgenden Zeitpunkten erhalten werden, häufig mit gleichen Intervallen zwischen ihnen. Es gibt verschiedene Zeiträume, z. B. jährlich, vierteljährlich, monatlich, wöchentlich und täglich. Für Zeitreihen des BIP (Bruttoinlandsprodukt) verwenden wir normalerweise vierteljährlich oder jährlich. Für Angebote - jährliche, monatliche und tägliche Häufigkeit. Mit dem folgenden Code können wir US-BIP-Daten sowohl vierteljährlich als auch für einen jährlichen Zeitraum abrufen:
ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual)
YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3
dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly)
DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9
Wir haben jedoch viele Fragen zur Zeitreihenanalyse. Aus makroökonomischer Sicht haben wir beispielsweise Geschäfts- oder Konjunkturzyklen. Branchen oder Unternehmen können saisonabhängig sein. In der Landwirtschaft werden die Landwirte beispielsweise im Frühjahr und Herbst mehr und im Winter weniger ausgeben. Für Einzelhändler hätten sie zum Jahresende einen enormen Cashflow.
Um Zeitreihen zu
bearbeiten , können wir die vielen nützlichen Funktionen des R-Pakets namens
timeSeries verwenden . Im Beispiel nehmen wir die täglichen Durchschnittsdaten mit einer wöchentlichen Häufigkeit:
library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean)
Wir könnten auch die Funktion
head () verwenden, um einige Beobachtungen zu sehen:
head(x)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700
head(y)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000
Vorhersage zukünftiger Ereignisse
Es gibt viele Methoden, die wir verwenden können, um die Zukunft vorherzusagen, z. B. gleitender Durchschnitt, Regression, Autoregression usw. Beginnen wir zunächst mit der einfachsten Methode für den gleitenden Durchschnitt:
movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) }
Im vorherigen Code ist der Standardwert für die Anzahl der Perioden 10. Wir könnten einen Datensatz namens MSFT verwenden, der im R-Paket
timeSeries enthalten ist (siehe folgenden Code):
library(timeSeries) data(MSFT) p<-MSFT$Close
[1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375
head(ma)
[1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167
mean(p[1:3])
[1] 60.75
mean(p[2:4])
[1] 60.25
Im manuellen Modus stellen wir fest, dass der Durchschnitt der ersten drei Werte von
x mit dem dritten Wert von
y übereinstimmt. In gewisser Weise könnten wir einen gleitenden Durchschnitt verwenden, um die Zukunft vorherzusagen.
Im folgenden Beispiel zeigen wir, wie die erwarteten Marktrenditen im nächsten Jahr bewertet werden. Hier verwenden wir den S & P500-Index und den historischen durchschnittlichen Jahreswert als unsere erwarteten Werte. Die ersten Befehle werden verwendet, um ein zugehöriges Dataset mit dem Namen
.sp500monthly zu laden. Ziel des Programms ist es, den durchschnittlichen Jahresdurchschnitt und das 90-Prozent-Konfidenzintervall zu ermitteln:
library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link))
[min mean max ]
cat(min2,ourMean,max2,"\n")
0.05032956 0.09022369 0.1301178
Wie Sie den Ergebnissen entnehmen können, beträgt die historische durchschnittliche jährliche Rendite für den S & P500 9%. Wir können jedoch nicht sagen, dass die Rentabilität des Index im nächsten Jahr 9% betragen wird, weil es kann zwischen 5% und 13% liegen, und dies sind enorme Schwankungen.
Saisonalität
Im folgenden Beispiel zeigen wir die Verwendung der Autokorrelation. Zunächst laden wir ein R-Paket namens
astsa herunter , das für angewandte statistische Zeitreihenanalyse steht. Dann laden wir das US-BIP vierteljährlich:
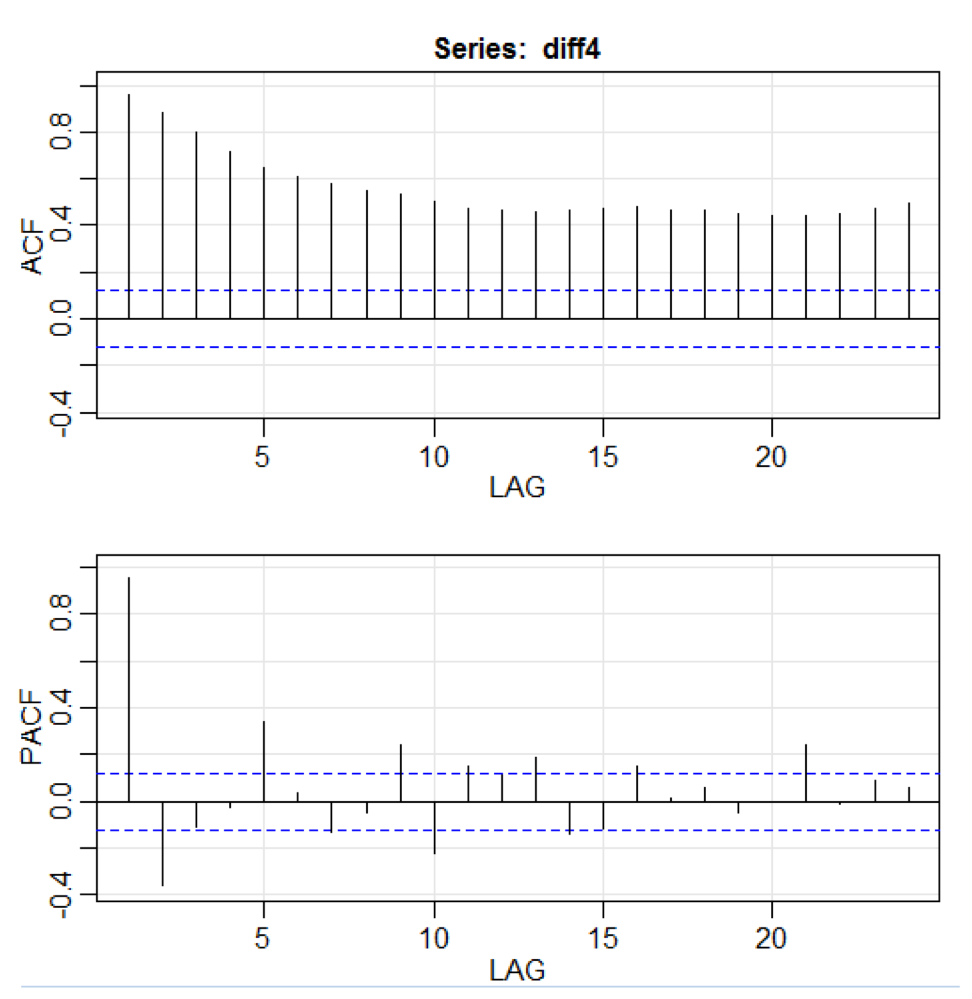
library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24)
Im obigen Code akzeptiert die Funktion
diff () die Differenz, z. B. den aktuellen Wert abzüglich des vorherigen Werts. Ein zweiter Eingabewert zeigt eine Verzögerung an. Eine Funktion namens
acf2 () wird zum Erstellen und Drucken der ACF- und PACF-Zeitreihen verwendet. ACF steht für Autokovarianzfunktion und PACF steht für partielle Autokorrelationsfunktion. Relevante Grafiken werden hier angezeigt:
Komponentenvisualisierung
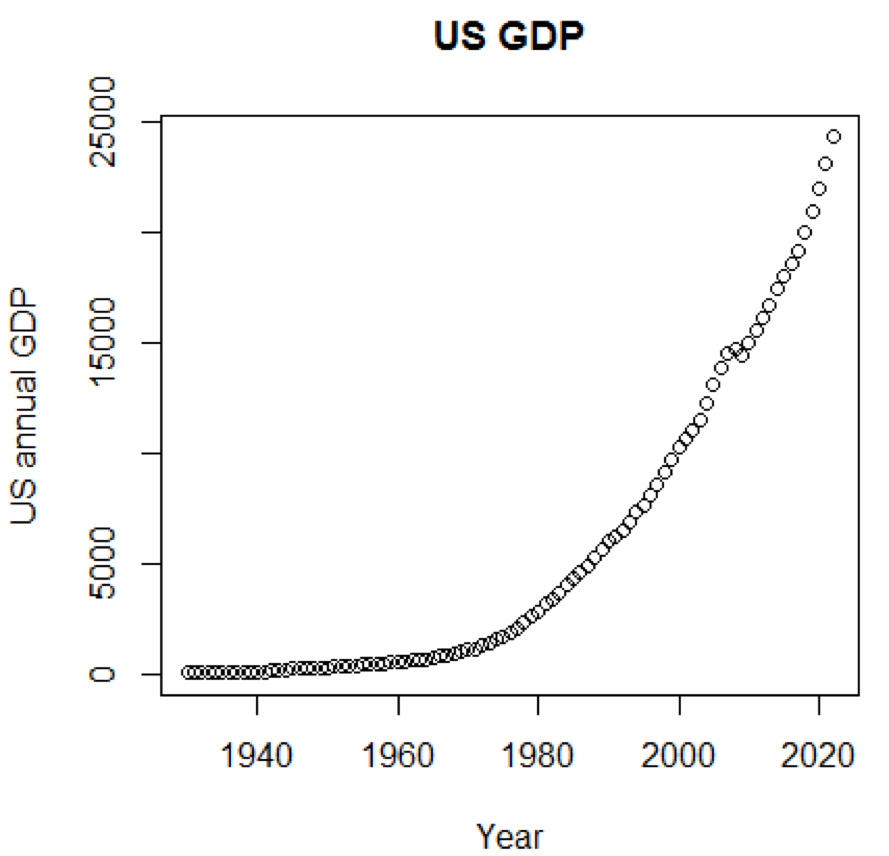
Es ist klar, dass Konzepte und Datensätze viel verständlicher wären, wenn wir Diagramme verwenden könnten. Das erste Beispiel zeigt Schwankungen des US-BIP in den letzten fünf Jahrzehnten:
path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle)
Der entsprechende Zeitplan wird hier angezeigt:
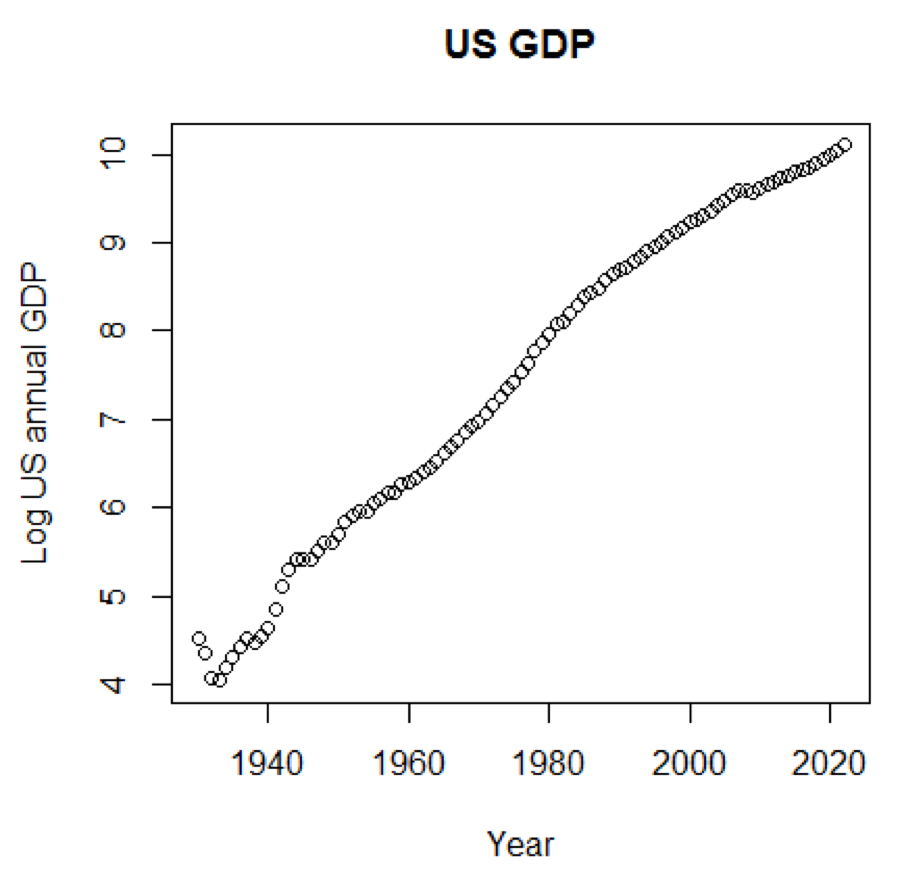
Wenn wir die logarithmische Skala für das BIP verwenden würden, hätten wir den folgenden Code und die folgende Grafik:
yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle)
Das folgende Diagramm befindet sich in der Nähe einer geraden Linie:
R-Paket - LiblineaR
Dieses Paket ist ein lineares Vorhersagemodell, das auf der LIBLINEAR C / C ++ - Bibliothek basiert. Hier ist ein Beispiel für die Verwendung des
Iris- Datensatzes. Das Programm versucht anhand von Trainingsdaten vorherzusagen, zu welcher Kategorie eine Anlage gehört:
library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE)
Die Schlussfolgerung lautet wie folgt. BCR ist eine ausgewogene Klassifizierungsrate. Für diese Wette gilt: Je höher desto besser:
cat("Best model type is:",bestType,"\n")
Best model type is: 4
cat("Best cost is:",bestCost,"\n")
Best cost is: 1
cat("Best accuracy is:",bestAcc,"\n")
Best accuracy is: 0.98
print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR)
[1] 0.95
R-Paket - Eclust
Dieses Paket ist ein mittelorientiertes Clustering für interpretierte Vorhersagemodelle in hochdimensionalen Daten. Schauen wir uns zunächst einen Datensatz namens
simdata an , der simulierte Daten für ein Paket enthält:
library(eclust) data("simdata") dim(simdata)
[1] 100 502
simdata[1:5, 1:6]
YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775
table(simdata[,"E"])
0 1 50 50
Die vorherige Schlussfolgerung zeigt, dass die Dimension der Daten 100 mal 502 beträgt.
Y ist der kontinuierliche Antwortvektor und
E ist die binäre Umgebungsvariable für die ECLUST-Methode.
E = 0 für unbelichtet (n = 50) und
E = 1 für belichtet (n = 50).
Das folgende Programm R wertet die Fisher-Z-Transformation aus:
library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score)
[1] 500 500
score[1:5,1:5]
Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000
Wir definieren die Fisher-Z-Transformation. Unter der Annahme, dass wir eine Menge von
n Paaren
x i und
y i haben , könnten wir ihre Korrelation unter Verwendung der folgenden Formel abschätzen:
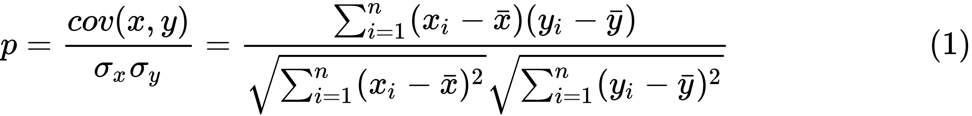
Hier ist
p die Korrelation zwischen zwei Variablen und

und
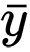
sind Stichprobenmittel für Zufallsvariablen
x und
y . Der Wert von
z ist definiert als:
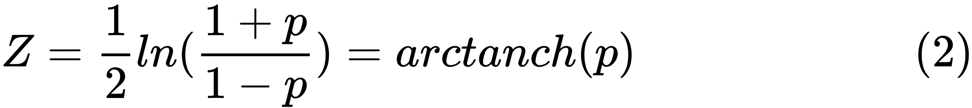 ln
ln ist die natürliche Logarithmusfunktion und
arctanh () ist die inverse hyperbolische Tangentenfunktion.
Modellauswahl
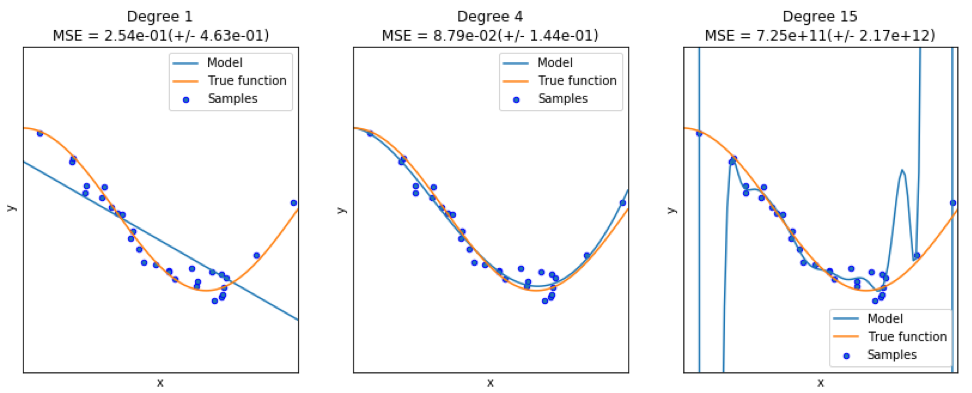
Wenn wir ein gutes Modell finden, sind wir manchmal mit einem Mangel / Überschuss an Daten konfrontiert. Das folgende Beispiel ist
hier ausgeliehen . Er zeigt die Probleme bei der Arbeit damit und wie wir die lineare Regression mit Polynommerkmalen verwenden können, um nichtlineare Funktionen zu approximieren. Spezifizierte Funktion:
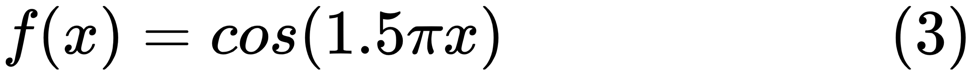
Im nächsten Programm versuchen wir, lineare und Polynommodelle zu verwenden, um eine Gleichung zu approximieren. Ein leicht modifizierter Code wird hier angezeigt. Das Programm zeigt die Auswirkungen von Datenmangel / Überangebot auf das Modell:
import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score
Die resultierenden Grafiken werden hier angezeigt:
Python-Paket - Modell-Laufsteg
Ein Beispiel finden Sie
hier .
Die ersten Codezeilen werden hier angezeigt:
import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine)
Die entsprechende Schlussfolgerung wird hier gezeigt. Um Platz zu sparen, wird nur der obere Teil dargestellt:
Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ----------------------------------------------------------------------
| Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined)
Python-Paket - sklearn
Da
sklearn ein sehr nützliches Paket ist, lohnt es sich, weitere Beispiele für die Verwendung dieses Pakets zu zeigen. Das hier gegebene Beispiel zeigt, wie das Paket verwendet wird, um Dokumente mithilfe des Bag-of-Word-Ansatzes nach Themen zu klassifizieren.
In diesem Beispiel wird die
scipy.sparse- Matrix zum Speichern von Objekten verwendet und es werden verschiedene Klassifizierer demonstriert, die spärliche Matrizen effizient verarbeiten können. In diesem Beispiel wird ein Datensatz mit 20 Newsgroups verwendet. Es wird automatisch heruntergeladen und dann zwischengespeichert. Die Zip-Datei enthält Eingabedateien und kann hier heruntergeladen
werden . Der Code ist
hier verfügbar. Um Platz zu sparen, werden nur die ersten Zeilen angezeigt:
import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel
Die entsprechende Ausgabe wird hier angezeigt:
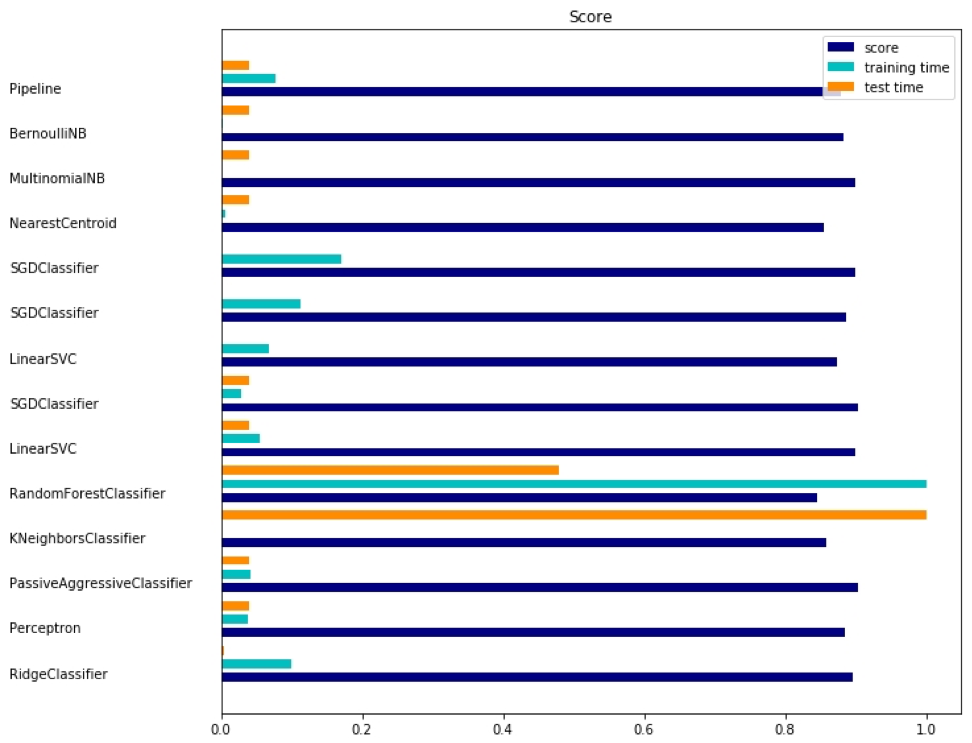
Für jede Methode gibt es drei Indikatoren: Bewertung, Schulungszeit und Testzeit.
Julia-Paket - QuantEcon
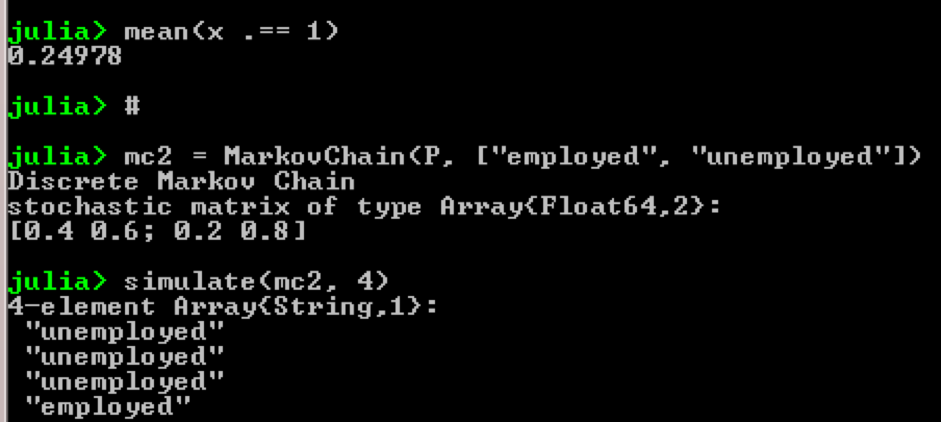
Nehmen Sie zum Beispiel die Verwendung von Markov-Ketten:
using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1)
Ergebnis:
Der Zweck des Beispiels ist zu sehen, wie sich eine Person von einem wirtschaftlichen Status in der Zukunft in einen anderen verwandelt. Schauen wir uns zunächst die folgende Tabelle an:
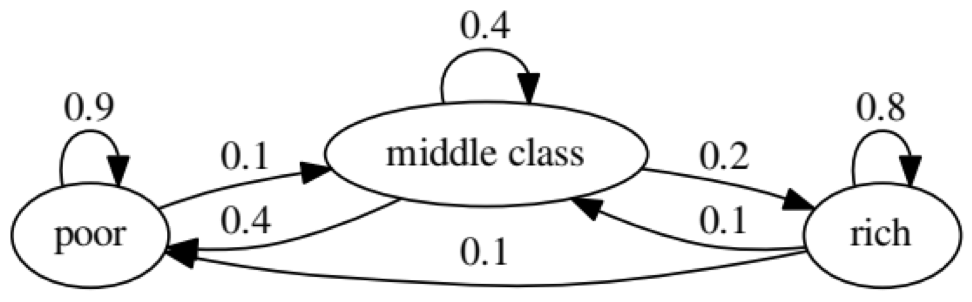
Schauen wir uns das Oval ganz links mit dem Status „schlecht“ an. 0,9 bedeutet, dass eine Person mit diesem Status eine 90% ige Chance hat, arm zu bleiben, und 10% gehen in die Mittelklasse. Es kann durch die folgende Matrix dargestellt werden: Bei Nullen gibt es keine Kante zwischen den Knoten:
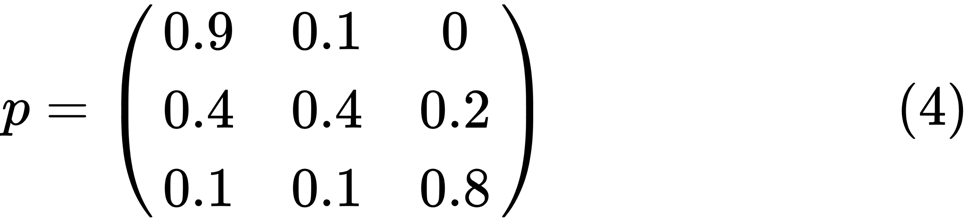
Es wird gesagt, dass zwei Zustände, x und y, miteinander in Beziehung stehen, wenn es positive ganze Zahlen j und k gibt, wie zum Beispiel:

Eine Markov-Kette
P heißt irreduzibel, wenn alle Zustände verbunden sind; das heißt, wenn
x und
y für jedes (x, y) gemeldet werden. Der folgende Code bestätigt dies:
using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc)
Die folgende Grafik stellt einen Extremfall dar, da der zukünftige Status einer armen Person zu 100% schlecht sein wird:

Der folgende Code bestätigt dies ebenfalls, da das Ergebnis
falsch ist :
using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2)
Granger-Kausaltest
Der Granger-Kausaltest wird verwendet, um festzustellen, ob eine Zeitreihe ein Faktor ist, und liefert nützliche Informationen zur Vorhersage der zweiten. Der folgende Code verwendet zur
Veranschaulichung einen
Datensatz mit dem Namen
ChickEgg . Der Datensatz enthält zwei Spalten, die Anzahl der Hühner und die Anzahl der Eier, mit einem Zeitstempel:
library(lmtest) data(ChickEgg) dim(ChickEgg)
[1] 54 2
ChickEgg[1:5,]
chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156
Die Frage ist, können wir die Anzahl der Eier in diesem Jahr verwenden, um die Anzahl der Hühner im nächsten Jahr vorherzusagen?
Wenn ja, dann ist die Anzahl der Hühner der Granger-Grund für die Anzahl der Eier. Wenn dies nicht der Fall ist, sagen wir, dass die Anzahl der Hühner kein Granger-Grund für die Anzahl der Eier ist. Hier ist der relevante Code:
library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg)
Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
In Modell 1 versuchen wir, Kükenverzögerungen plus Eierverzögerungen zu verwenden, um die Anzahl der Küken zu erklären.
Weil Der Wert von
P ist ziemlich klein (er ist mit 0,01 signifikant). Wir sagen, dass die Anzahl der Eier der Granger-Grund für die Anzahl der Hühner ist.
Der folgende Test zeigt, dass Daten zu Hühnern nicht zur Vorhersage des folgenden Zeitraums verwendet werden können:
grangertest(egg~chicken, order = 3, data = ChickEgg)
Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238
Im folgenden Beispiel überprüfen wir die Rentabilität von IBM und dem S & P500, um herauszufinden, ob sie Granger-Grund für einen anderen sind.
Zunächst definieren wir die Ertragsfunktion:
ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) }
>x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final)
DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933
Jetzt kann die Funktion mit Eingabewerten aufgerufen werden. Ziel des Programms ist es zu testen, ob wir Marktverzögerungen verwenden können, um die Rentabilität von IBM zu erklären. Auf die gleiche Weise überprüfen wir die Verzögerung der Markteinnahmen von IBM:
library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final)
Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Die Ergebnisse zeigen, dass der S & P500 verwendet werden kann, um die Rentabilität von IBM für den nächsten Zeitraum zu erklären, da er mit 0,1% statistisch signifikant ist. Mit dem folgenden Code wird überprüft, ob die Verzögerung von IBM die Änderung im S & P500 erklärt:
grangertest(RET_MKT ~ RET_IBM, order = 1, data =final)
Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Das Ergebnis legt nahe, dass während dieses Zeitraums die Renditen von IBM verwendet werden können, um den S & P500-Index für den nächsten Zeitraum zu erläutern.