Vorwort

In diesem Artikel werden wir verschiedene Aspekte von SVM untersuchen:
- theoretische Komponente von SVM;
- wie der Algorithmus bei Stichproben funktioniert, die nicht linear in Klassen unterteilt werden können;
- Python-Beispiel und Implementierung des Algorithmus in der SciKit Learn-Bibliothek.
In den folgenden Artikeln werde ich versuchen, über die mathematische Komponente dieses Algorithmus zu sprechen.
Wie Sie wissen, werden maschinelle Lernaufgaben in zwei Hauptkategorien unterteilt - Klassifizierung und Regression. Abhängig davon, mit welcher dieser Aufgaben wir konfrontiert sind und welchen Datensatz wir für diese Aufgabe haben, wählen wir den zu verwendenden Algorithmus aus.
Die Support Vector Machines-Methode oder SVM (von den englischen Support Vector Machines) ist ein linearer Algorithmus, der bei Klassifizierungs- und Regressionsproblemen verwendet wird. Dieser Algorithmus ist in der Praxis weit verbreitet und kann sowohl lineare als auch nichtlineare Probleme lösen. Das Wesen der „Maschinen“ von Unterstützungsvektoren ist einfach: Der Algorithmus erstellt eine Linie oder Hyperebene, die die Daten in Klassen unterteilt.
Theorie
Die Hauptaufgabe des Algorithmus besteht darin, die korrekteste Linie oder Hyperebene zu finden und die Daten in zwei Klassen zu unterteilen. SVM ist ein Algorithmus, der Daten am Eingang empfängt und eine solche Trennlinie zurückgibt.
Betrachten Sie das folgende Beispiel. Angenommen, wir haben einen Datensatz und möchten die roten Quadrate von den blauen Kreisen klassifizieren und trennen (sagen wir positiv und negativ). Das Hauptziel dieser Aufgabe wird es sein, die „ideale“ Linie zu finden, die diese beiden Klassen trennt.
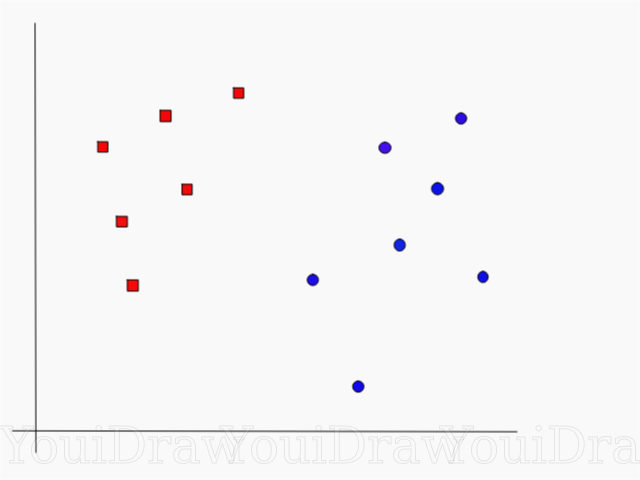
Suchen Sie die perfekte Linie oder Hyperebene, die den Datensatz in blaue und rote Klassen unterteilt.
Auf den ersten Blick ist es nicht so schwierig, oder?
Aber wie Sie sehen, gibt es keine einzige Linie, die ein solches Problem lösen könnte. Wir können unendlich viele Zeilen aufnehmen, die diese beiden Klassen trennen können. Wie genau findet SVM die „ideale“ Linie und was ist in ihrem Verständnis „ideal“?
Schauen Sie sich das folgende Beispiel an und überlegen Sie, welche der beiden Linien (gelb oder grün) die beiden Klassen am besten trennt und zur Beschreibung des „Ideals“ passt.
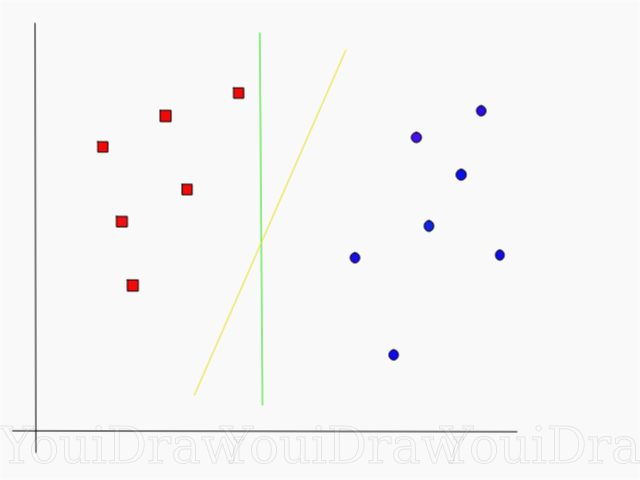
Welche Zeile trennt den Datensatz Ihrer Meinung nach besser?
Wenn Sie die gelbe Linie gewählt haben, gratuliere ich Ihnen: Dies ist die Linie, die der Algorithmus wählen würde. In diesem Beispiel können wir intuitiv verstehen, dass die gelbe Linie die beiden Klassen besser trennt und entsprechend klassifiziert als die grüne.
Bei der grünen Linie befindet sie sich zu nahe an der roten Klasse. Trotz der Tatsache, dass sie alle Objekte des aktuellen Datensatzes korrekt klassifiziert hat, wird eine solche Zeile nicht verallgemeinert - sie verhält sich nicht so gut wie ein unbekannter Datensatz. Die Aufgabe, eine verallgemeinerte Trennung zwischen zwei Klassen zu finden, ist eine der Hauptaufgaben beim maschinellen Lernen.
Wie SVM die beste Linie findet
Der SVM-Algorithmus ist so konzipiert, dass er nach Punkten im Diagramm sucht, die sich direkt an der nächstgelegenen Trennlinie befinden. Diese Punkte werden Referenzvektoren genannt. Dann berechnet der Algorithmus den Abstand zwischen den Stützvektoren und der Teilungsebene. Dies ist der Abstand, der als Lücke bezeichnet wird. Das Hauptziel des Algorithmus ist die Maximierung des Abstandes. Die beste Hyperebene wird als Hyperebene betrachtet, für die diese Lücke so groß wie möglich ist.

Ziemlich einfach, oder? Betrachten Sie das folgende Beispiel mit einem komplexeren Datensatz, der nicht linear geteilt werden kann.
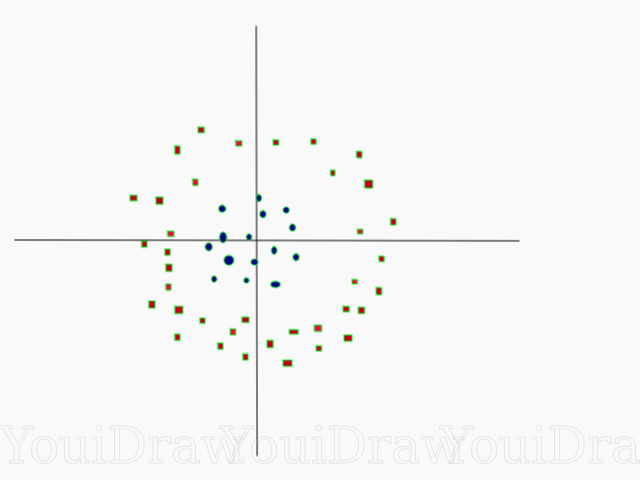
Offensichtlich kann dieser Datensatz nicht linear geteilt werden. Wir können keine gerade Linie zeichnen, die diese Daten klassifizieren würde. Dieser Datensatz kann jedoch linear geteilt werden, indem eine zusätzliche Dimension hinzugefügt wird, die wir als Z-Achse bezeichnen. Stellen Sie sich vor, die Koordinaten auf der Z-Achse werden durch die folgende Einschränkung reguliert:
Somit wird die Ordinate Z vom Quadrat des Abstandes des Punktes zum Anfang der Achse dargestellt.
Unten sehen Sie eine Visualisierung desselben Datensatzes auf der Z-Achse.
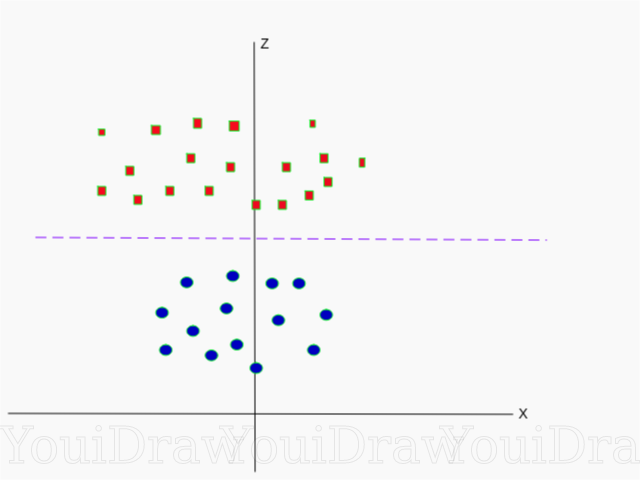
Jetzt können die Daten linear aufgeteilt werden. Angenommen, die Magenta-Linie trennt die Daten z = k, wobei k eine Konstante ist. Wenn
dann
- Kreisformel. Auf diese Weise können wir unseren linearen Teiler mithilfe dieser Transformation auf die ursprüngliche Anzahl der Probendimensionen zurückprojizieren.
Infolgedessen können wir einen nichtlinearen Datensatz klassifizieren, indem wir ihm eine zusätzliche Dimension hinzufügen und ihn dann mithilfe der mathematischen Transformation wieder in seine ursprüngliche Form bringen. Nicht bei allen Datensätzen ist es jedoch genauso einfach, eine solche Transformation in Gang zu setzen. Glücklicherweise löst die Implementierung dieses Algorithmus in der sklearn-Bibliothek dieses Problem für uns.
Hyperebene
Nachdem wir uns mit der Logik des Algorithmus vertraut gemacht haben, fahren wir mit der formalen Definition einer Hyperebene fort
Eine Hyperebene ist eine n-1-dimensionale Unterebene in einem n-dimensionalen euklidischen Raum, der den Raum in zwei separate Teile unterteilt.
Stellen Sie sich zum Beispiel vor, dass unsere Linie als eindimensionaler euklidischer Raum dargestellt wird (d. H. Unser Datensatz liegt auf einer geraden Linie). Wählen Sie einen Punkt auf dieser Linie. Dieser Punkt teilt den Datensatz, in unserem Fall die Linie, in zwei Teile. Die Linie hat einen Takt und der Punkt hat 0 Takte. Daher ist ein Punkt eine Hyperebene einer Linie.
Für den zweidimensionalen Datensatz, den wir zuvor getroffen haben, war die Trennlinie dieselbe Hyperebene. Einfach ausgedrückt, für einen n-dimensionalen Raum gibt es eine n-1-dimensionale Hyperebene, die diesen Raum in zwei Teile teilt.
CODE
import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2])
Punkte werden als Array von X und die Klassen, zu denen sie gehören, als Array von y dargestellt.
Jetzt werden wir unser Modell mit diesem Beispiel trainieren. In diesem Beispiel habe ich den linearen Parameter des „Kernels“ des Klassifikators (Kernels) festgelegt.
from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y)
Klassenvorhersage eines neuen Objekts
prediction = clf.predict([[0,6]])
Parametereinstellung
Parameter sind die Argumente, die Sie beim Erstellen des Klassifikators übergeben. Im Folgenden habe ich einige der wichtigsten benutzerdefinierten SVM-Einstellungen angegeben:
"C"Dieser Parameter hilft dabei, diese feine Linie zwischen „Glätte“ und der Genauigkeit der Klassifizierung von Objekten in der Trainingsprobe anzupassen. Je höher der C-Wert ist, desto mehr Objekte im Trainingssatz werden korrekt klassifiziert.

In diesem Beispiel gibt es mehrere Entscheidungsschwellen, die wir für diese bestimmte Stichprobe definieren können. Achten Sie auf die direkte Entscheidungsschwelle (in der Tabelle als grüne Linie dargestellt). Es ist ganz einfach und aus diesem Grund wurden mehrere Objekte falsch klassifiziert. Diese falsch klassifizierten Punkte werden in den Daten als Ausreißer bezeichnet.
Wir können die Parameter auch so einstellen, dass wir am Ende eine stärker gekrümmte Linie (hellblaue Entscheidungsschwelle) erhalten, die absolut alle Trainingsmusterdaten korrekt klassifiziert. In diesem Fall sind die Chancen, dass unser Modell in der Lage sein wird, neue Daten zu verallgemeinern und gleich gute Ergebnisse zu erzielen, natürlich katastrophal gering. Wenn Sie also versuchen, beim Training des Modells Genauigkeit zu erreichen, sollten Sie etwas Gleichmäßigeres und Direkteres anstreben. Je höher die C-Zahl ist, desto stärker ist die Hyperebene in Ihrem Modell verwickelt, aber desto höher ist die Anzahl der korrekt klassifizierten Objekte im Trainingssatz. Daher ist es wichtig, die Modellparameter für einen bestimmten Datensatz zu „verdrehen“, um eine Umschulung zu vermeiden und gleichzeitig eine hohe Genauigkeit zu erzielen.
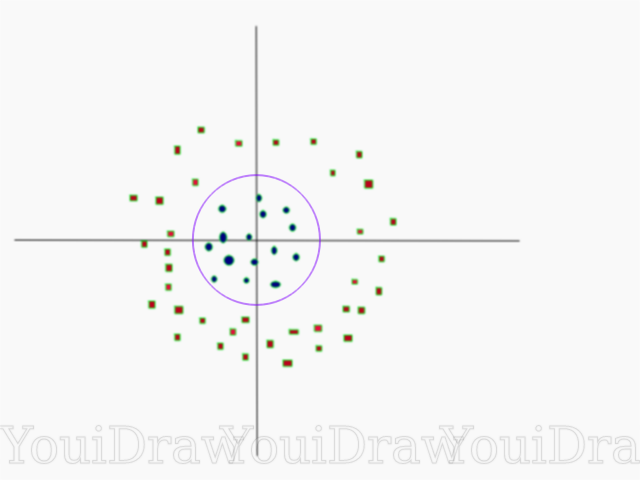
GammaIn der offiziellen Dokumentation der SciKit Learn-Bibliothek heißt es, dass das Gamma bestimmt, inwieweit jedes der Elemente im Datensatz einen Einfluss auf die Bestimmung der „idealen Linie“ hat. Je niedriger das Gamma, desto mehr Elemente, auch diejenigen, die weit genug von der Trennlinie entfernt sind, nehmen an der Auswahl dieser Linie teil. Wenn das Gamma hoch ist, "verlässt" sich der Algorithmus nur auf die Elemente, die der Linie selbst am nächsten liegen.
Wenn der Gammapegel zu hoch eingestellt ist, nehmen nur die Elemente, die der Linie am nächsten liegen, am Entscheidungsprozess an der Position der Linie teil. Dies hilft, Ausreißer in den Daten zu ignorieren. Der SVM-Algorithmus ist so konzipiert, dass die Punkte, die am nächsten beieinander liegen, bei einer Entscheidung mehr Gewicht haben. Mit den richtigen Einstellungen für "C" und "Gamma" kann jedoch ein optimales Ergebnis erzielt werden, das eine linearere Hyperebene erzeugt, die Ausreißer ignoriert und daher allgemeiner ist.
Fazit
Ich hoffe aufrichtig, dass dieser Artikel Ihnen geholfen hat, die Essenz der Arbeit von SVM oder der Referenzvektormethode zu verstehen. Ich erwarte von Ihnen Kommentare und Ratschläge. In nachfolgenden Veröffentlichungen werde ich über die mathematische Komponente von SVM und Optimierungsprobleme sprechen.
Quellen:
Offizielle SVM-Dokumentation in SciKit LearnTowardsDataScience BlogSiraj Raval: Unterstützen Sie VektormaschinenEinführung in das maschinelle Lernen Udacity SVM: GammakursvideoWikipedia: SVM