Quelle : Wikipedia-Lizenz CC-BY-SA 3.0

Wenn Sie häufig mit öffentlichen Verkehrsmitteln anreisen, sind Sie wahrscheinlich auf folgende Situation gestoßen:

Du kommst zum Stillstand. Es steht geschrieben, dass der Bus alle 10 Minuten fährt. Beachten Sie die Zeit ... Endlich, nach 11 Minuten, kommt der Bus und der Gedanke: Warum habe ich immer Pech?

Wenn Busse alle 10 Minuten ankommen und Sie zu einer zufälligen Zeit ankommen, sollte die durchschnittliche Wartezeit theoretisch etwa 5 Minuten betragen. In Wirklichkeit kommen die Busse jedoch nicht pünktlich an, sodass Sie länger warten können. Es stellt sich heraus, dass man mit einigen vernünftigen Annahmen zu einem überraschenden Ergebnis kommen kann:

Wenn Sie auf einen Bus warten, der durchschnittlich alle 10 Minuten ankommt, beträgt Ihre durchschnittliche Wartezeit 10 Minuten.

Dies wird manchmal als Wartezeitparadox bezeichnet .

Ich hatte vorher eine Idee und habe mich immer gefragt, ob das wirklich stimmt ... wie sehr entsprechen solche „vernünftigen Annahmen“ der Realität? In diesem Artikel untersuchen wir das Latenzparadoxon sowohl im Hinblick auf Modellierung als auch auf probabilistische Argumente und werfen dann einen Blick auf einige der tatsächlichen Busdaten in Seattle, um das Paradoxon (hoffentlich) ein für alle Mal zu lösen.

Paradoxe Inspektion

Wenn die Busse genau alle zehn Minuten ankommen, beträgt die durchschnittliche Wartezeit 5 Minuten. Man kann leicht verstehen, warum das Hinzufügen von Variationen zum Intervall zwischen Bussen die durchschnittliche Wartezeit erhöht.

Das Wartezeitparadoxon ist ein Sonderfall eines allgemeineren Phänomens - das Inspektionsparadoxon , das in Allen Downeys vernünftigem Artikel "Das Inspektionsparadoxon überall um uns herum" ausführlich erörtert wird.

Kurz gesagt, das Inspektionsparadoxon tritt immer dann auf, wenn die Wahrscheinlichkeit der Beobachtung einer Menge mit der beobachteten Menge zusammenhängt. Allen gibt ein Beispiel für eine Umfrage unter Universitätsstudenten über die durchschnittliche Größe ihrer Klassen. Obwohl die Schule wahrheitsgemäß von einer durchschnittlichen Anzahl von 30 Schülern in einer Gruppe spricht, ist die durchschnittliche Gruppengröße aus Sicht der Schüler viel größer. Der Grund ist, dass es in großen Klassen (natürlich) mehr Schüler gibt, was bei ihrer Umfrage festgestellt wird.

Bei einem Busfahrplan mit einem angegebenen 10-Minuten-Intervall ist das Intervall zwischen den Ankünften manchmal länger als 10 Minuten und manchmal kürzer. Und wenn Sie zu einem zufälligen Zeitpunkt zum Stillstand kommen, ist es wahrscheinlicher, dass Sie auf ein längeres Intervall stoßen als auf ein kürzeres. Daher ist es logisch, dass das durchschnittliche Zeitintervall zwischen Warteintervallen länger ist als das durchschnittliche Zeitintervall zwischen Bussen, da längere Intervalle in der Stichprobe häufiger vorkommen.

Das Latenzparadoxon macht jedoch eine stärkere Aussage: Wenn der durchschnittliche Busabstand ist $$$N$ Minuten beträgt die durchschnittliche Wartezeit für Passagiere $$$2N$ Minuten. Könnte das wahr sein?

Simulation der Latenz

Um uns davon zu überzeugen, simulieren wir zunächst den Busfluss, der in durchschnittlich 10 Minuten ankommt. Nehmen Sie für die Genauigkeit eine große Stichprobe: eine Million Busse (oder etwa 19 Jahre 10-minütiger Verkehr rund um die Uhr):

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N)) 

Überprüfen Sie, ob das durchschnittliche Intervall nahe bei liegt $$$\ tau = 10$ ::

 intervals = np.diff(bus_arrival_times) intervals.mean() 

9.9999879601518398

Jetzt können wir die Ankunft einer großen Anzahl von Fahrgästen an einer Bushaltestelle während dieser Zeit simulieren und die Wartezeit berechnen, die jeder von ihnen erlebt. Kapseln Sie den Code in eine Funktion zur späteren Verwendung:

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times 

Dann simulieren wir die Wartezeit und berechnen den Durchschnitt:

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean() 

10.001584206227317

Die durchschnittliche Wartezeit beträgt fast 10 Minuten, wie das Paradox vorausgesagt hat.

Tiefer graben: Wahrscheinlichkeiten und Poisson-Prozesse

Wie kann man eine solche Situation simulieren?

Tatsächlich ist dies ein Beispiel für ein Inspektionsparadoxon, bei dem die Wahrscheinlichkeit, einen Wert zu beobachten, mit dem Wert selbst zusammenhängt. Bezeichnen mit $$$p (T)$ Abstand $$$T$ zwischen den Bussen, wenn sie an der Bushaltestelle ankommen. In einem solchen Datensatz beträgt der erwartete Wert der Ankunftszeit:

$$

$$E [T] = \ int_0 ^ \ infty T ~ p (T) ~ dT$$

In der vorherigen Simulation haben wir ausgewählt $$$E [T] = \ tau = 10$ Minuten.

Wenn ein Passagier zu irgendeinem Zeitpunkt an einer Bushaltestelle ankommt, hängt die Wahrscheinlichkeit einer Wartezeit nicht nur davon ab $$$p (T)$ aber auch von $$$T$ : Je größer das Intervall, desto mehr Passagiere befinden sich darin.

So können wir die Verteilung der Ankunftszeit aus Sicht der Passagiere schreiben:

$$

$$p_ {exp} (T) \ propto T ~ p (T)$$

Die Proportionalitätskonstante ergibt sich aus der Normalisierung der Verteilung:

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {\ int_0 ^ \ infty T ~ p (T) ~ dT}$$

Es vereinfacht sich

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {E [T]}$$

Dann die Wartezeit $$$E [W]$ wird die Hälfte des erwarteten Intervalls für Passagiere sein, damit wir aufzeichnen können

$$

$$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T ~ p_ {exp} (T) ~ dT$$

was verständlicher umgeschrieben werden kann:

$$

$$E [W] = \ frac {E [T ^ 2]} {2E [T]}$$

und jetzt bleibt nur noch ein Formular für zu wählen $$$p (T)$ und berechnen Sie die Integrale.

Die Wahl von p (T)

Nachdem Sie ein formales Modell erhalten haben, wofür ist eine angemessene Verteilung? $$$p (T)$ ? Wir werden ein Bild der Verteilung zeichnen $$$p (T)$ innerhalb unserer simulierten Ankünfte durch Zeichnen eines Histogramms der Intervalle zwischen Ankünften:

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density'); 

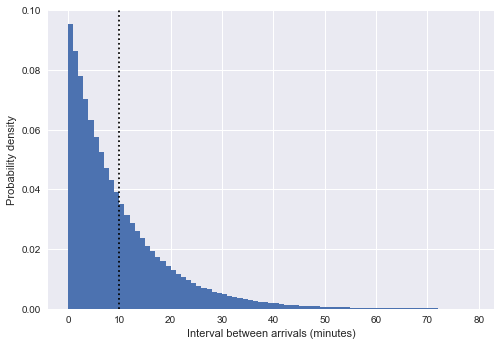
Hier zeigt die vertikale gestrichelte Linie ein durchschnittliches Intervall von etwa 10 Minuten. Dies ist einer Exponentialverteilung sehr ähnlich und nicht zufällig: Unsere Simulation der Busankunftszeit in Form einheitlicher Zufallszahlen kommt dem Poisson-Prozess sehr nahe, und für einen solchen Prozess ist die Verteilung der Intervalle exponentiell.

(Hinweis: In unserem Fall ist dies nur ein ungefährer Exponent, in der Tat die Intervalle $$$T$ zwischen $$$N$ gleichmäßig ausgewählte Punkte innerhalb einer Zeitspanne $$$N \ tau$ Match Beta-Verteilung $$$T / (N \ tau) \ sim \ mathrm {Beta} [1, N]$ Das ist in der großen Grenze $$$N$ Annäherung $$$T \ sim \ mathrm {Exp} [1 / \ tau]$ . Für weitere Informationen können Sie beispielsweise einen Beitrag auf StackExchange oder diesen Thread auf Twitter lesen.

Die exponentielle Verteilung der Intervalle impliziert, dass die Ankunftszeit dem Poisson-Prozess folgt. Um diese Argumentation zu überprüfen, überprüfen wir das Vorhandensein einer anderen Eigenschaft des Poisson-Prozesses: Die Anzahl der Ankünfte über einen festgelegten Zeitraum ist eine Poisson-Verteilung. Dazu teilen wir die simulierten Ankünfte in Zeitblöcke ein:

 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend(); 

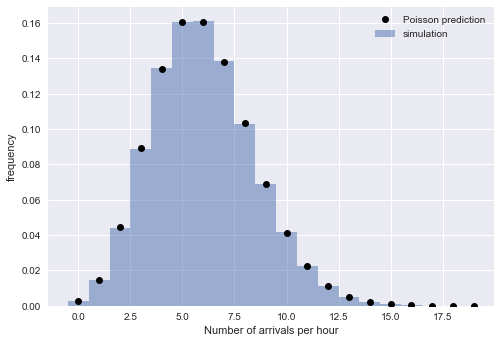
Die enge Übereinstimmung von empirischen und theoretischen Werten überzeugt uns von der Richtigkeit unserer Interpretation: für große $$$N$ Die simulierte Ankunftszeit wird durch den Poisson-Prozess gut beschrieben, der exponentiell verteilte Intervalle impliziert.

Dies bedeutet, dass die Wahrscheinlichkeitsverteilung geschrieben werden kann:

$$

$$p (T) = \ frac {1} {\ tau} e ^ {- T / \ tau}$$

Wenn wir das Ergebnis in der vorherigen Formel ersetzen, finden wir die durchschnittliche Wartezeit für Passagiere an der Haltestelle:

$$

$$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2 ~ e ^ {- T / \ tau}} {2 \ int_0 ^ \ infty T ~ e ^ {- T / \ tau}} = \ frac {2 \ tau ^ 3} {2 (\ tau ^ 2)} = \ tau$$

Bei Flügen mit Ankünften über den Poisson-Prozess ist die erwartete Wartezeit identisch mit dem durchschnittlichen Intervall zwischen Ankünften.

Dieses Problem kann wie folgt argumentiert werden: Der Poisson-Prozess ist ein Prozess ohne Speicher , dh der Verlauf von Ereignissen hat nichts mit der erwarteten Zeit des nächsten Ereignisses zu tun. Daher ist bei Ankunft an einer Bushaltestelle die durchschnittliche Wartezeit für einen Bus immer dieselbe: In unserem Fall sind es 10 Minuten, unabhängig davon, wie viel Zeit seit dem letzten Bus vergangen ist! Es spielt keine Rolle, wie lange Sie gewartet haben: Die erwartete Zeit bis zum nächsten Bus beträgt immer genau 10 Minuten. Beim Poisson-Prozess erhalten Sie keine Gutschrift für die Wartezeit.

Reality Timeout

Das Obige ist gut, wenn die tatsächlichen Busankünfte tatsächlich durch den Poisson-Prozess beschrieben werden, aber ist das so?


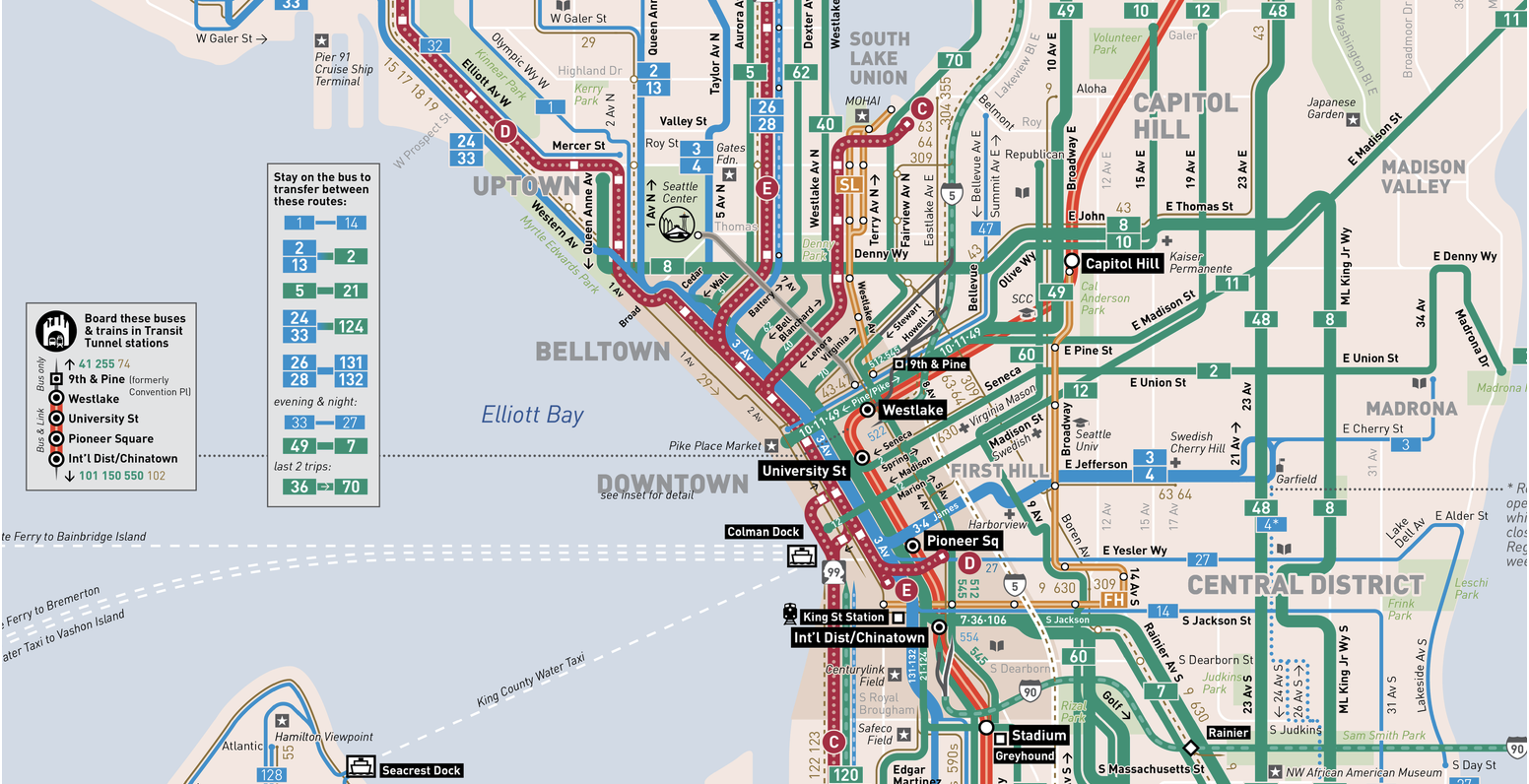Quelle: Seattle Public Transport Scheme

Versuchen wir herauszufinden, wie das Paradox der Wartezeit mit der Realität übereinstimmt. Zu diesem Zweck untersuchen wir einige der Daten, die hier zum Download zur Verfügung stehen: Arrival_Times.csv (3 MB CSV-Datei). Der Datensatz enthält die geplanten und tatsächlichen Ankunftszeiten für die RapidRide- Busse C, D und E an der 3rd & Pike-Bushaltestelle in der Innenstadt von Seattle. Die Daten wurden im zweiten Quartal 2016 aufgezeichnet (vielen Dank an Mark Hallenback vom Washington State Transportation Center für diese Datei!).

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head() 

	OPD_DATE	FAHRZEUG_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	S.	30908177	431	3. AVE & PIKE ST (431)	01:11:57	01:13:19
1	2016-03-26	6201	673	S.	30908033	431	3. AVE & PIKE ST (431)	23:19:57	23:16:13
2	2016-03-26	6201	673	S.	30908028	431	3. AVE & PIKE ST (431)	21:19:57	21:18:46
3	2016-03-26	6201	673	S.	30908019	431	3. AVE & PIKE ST (431)	19:04:57	19:01:49
4	2016-03-26	6201	673	S.	30908252	431	3. AVE & PIKE ST (431)	16:42:57	16:42:39

Ich habe mich für die RapidRide-Daten entschieden, auch weil die Busse den größten Teil des Tages in regelmäßigen Abständen von 10 bis 15 Minuten fahren, ganz zu schweigen von der Tatsache, dass ich ein häufiger Passagier der Route C bin.

Datenbereinigung

Zunächst führen wir eine kleine Datenbereinigung durch, um sie in eine praktische Ansicht zu konvertieren:

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head() 

	Route	Richtung	Grafik	Tatsache Ankunft	Verspätung (min)
0	C.	Süden	2016-03-26 01:11:57	2016-03-26 01:13:19	1,366667
1	C.	Süden	2016-03-26 23:19:57	2016-03-26 23:16:13	-3,733333
2	C.	Süden	2016-03-26 21:19:57	2016-03-26 21:18:46	-1,183333
3	C.	Süden	2016-03-26 19:04:57	2016-03-26 19:01:49	-3,133333
4	C.	Süden	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

Wie spät sind die Busse?

Diese Tabelle enthält sechs Datensätze: Nord- und Südrichtung für jede Route C, D und E. Um eine Vorstellung von ihren Eigenschaften zu erhalten, erstellen wir für jede dieser sechs Routen ein Histogramm der tatsächlichen abzüglich der geplanten Ankunftszeit:

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses'); 

Es ist logisch anzunehmen, dass die Busse zu Beginn der Strecke näher am Fahrplan liegen und gegen Ende stärker vom Fahrplan abweichen. Die Daten bestätigen dies: Unser Stopp auf der südlichen Route C sowie auf der nördlichen Route D und E befindet sich nahe am Beginn der Route und in der entgegengesetzten Richtung, nicht weit vom endgültigen Ziel entfernt.

Geplante und beobachtete Intervalle

Sehen Sie sich die beobachteten und geplanten Busintervalle für diese sechs Strecken an. Beginnen wir mit der groupby Funktion in Pandas, um diese Intervalle zu berechnen:

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway) 

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses'); 

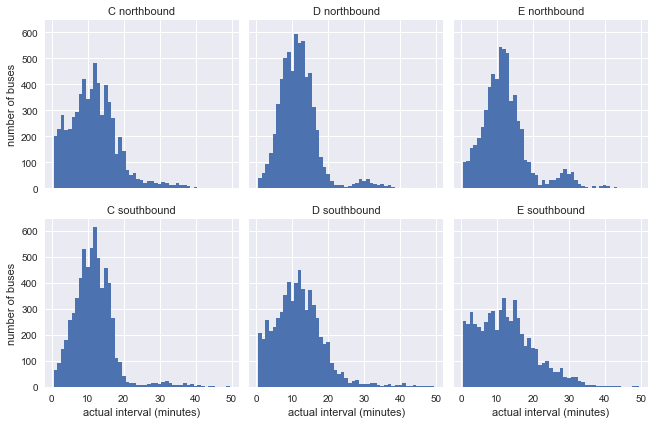
Es ist bereits offensichtlich, dass die Ergebnisse der Exponentialverteilung unseres Modells nicht sehr ähnlich sind, aber dies sagt immer noch nichts aus: Die Verteilungen können durch inkonsistente Intervalle in der Grafik beeinflusst werden.

Wiederholen wir die Erstellung von Diagrammen unter Berücksichtigung der geplanten und nicht der beobachteten Ankunftsintervalle:

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency'); 

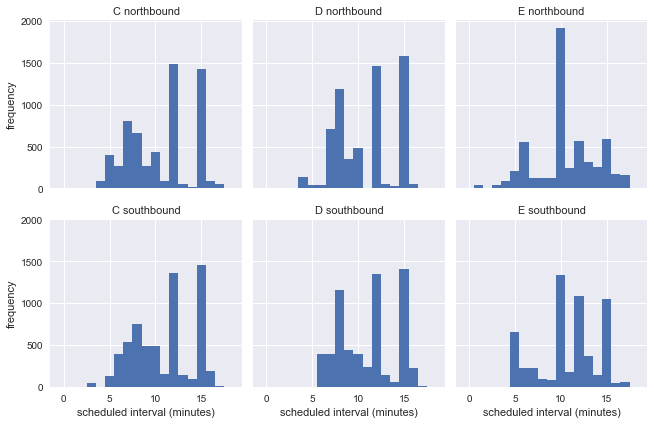
Dies zeigt, dass Busse während der Woche in unterschiedlichen Intervallen verkehren, sodass wir die Genauigkeit des Wartezeitparadoxons nicht anhand realer Informationen von der Bushaltestelle abschätzen können.

Aufbau einheitlicher Zeitpläne

Obwohl der offizielle Fahrplan keine einheitlichen Intervalle vorsieht, gibt es mehrere spezifische Zeitintervalle mit einer großen Anzahl von Bussen: Zum Beispiel fast 2.000 E-Linienbusse in Richtung Norden mit einem geplanten Intervall von 10 Minuten. Um herauszufinden, ob das Latenzparadoxon anwendbar ist, gruppieren wir die Daten in Routen, Richtungen und das geplante Intervall und stapeln sie dann neu, als ob sie nacheinander aufgetreten wären. Dies sollte alle relevanten Merkmale der Quelldaten beibehalten und gleichzeitig einen direkten Vergleich mit den Vorhersagen des Latenzparadoxons ermöglichen.

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head() 

	Route	Richtung	Zeitplan	Tatsache Ankunft	Verspätung (min)	Tatsache Intervall	Geplantes Intervall
0	C.	Norden	10.0	12.400000	2.400.000	NaN	10.0
1	C.	Norden	20.0	27.150000	7.150000	0,183333	10.0
2	C.	Norden	30.0	26.966667	-3.033333	14.566667	10.0
3	C.	Norden	40.0	35,516667	-4,483333	8.366667	10.0
4	C.	Norden	50.0	53,583333	3,583333	18.066667	10.0

Anhand der gelöschten Daten können Sie ein Diagramm der Verteilung des tatsächlichen Erscheinungsbilds von Bussen entlang jeder Route und Richtung mit einer Häufigkeit der Ankunft erstellen:

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14) 

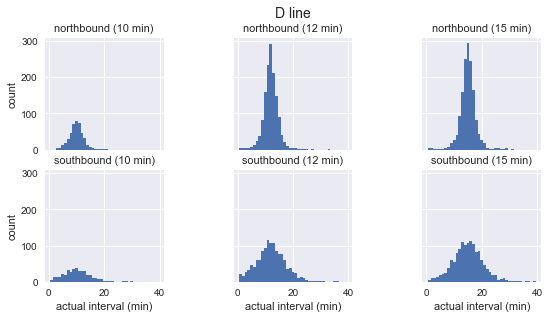
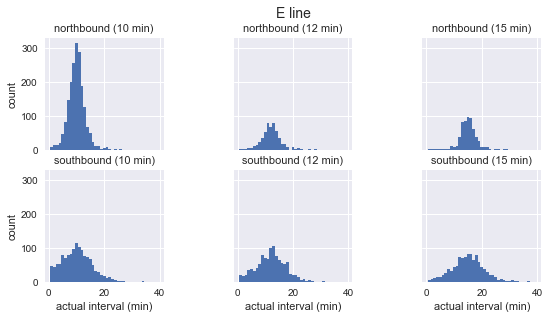
Wir sehen, dass für jede Route die Verteilung der beobachteten Intervalle fast Gaußsch ist. Sie erreicht ihren Höhepunkt in der Nähe des geplanten Intervalls und weist eine Standardabweichung auf, die am Anfang der Route geringer ist (Süden für C, Norden für D / E) und am Ende mehr. Selbst beim Sehen entsprechen die tatsächlichen Ankunftsintervalle definitiv nicht der Exponentialverteilung, die die Hauptannahme ist, auf der das Wartezeitparadoxon basiert.

Wir können die oben verwendete Wartezeitsimulationsfunktion verwenden, um die durchschnittliche Wartezeit für jede Busroute, Richtung und Fahrplan zu ermitteln:

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std())) 

  Geplantes Intervall für die Routenrichtung
 C Nord 10,0 7,8 +/- 12,5
                       12,0 7,4 +/- 5,7
                       15,0 8,8 +/- 6,4
          Süd 10,0 6,2 +/- 6,3
                       12,0 6,8 +/- 5,2
                       15,0 8,4 +/- 7,3
 D Nord 10,0 6,1 +/- 7,1
                       12,0 6,5 +/- 4,6
                       15,0 7,9 +/- 5,3
          Süd 10,0 6,7 +/- 5,3
                       12,0 7,5 +/- 5,9
                       15,0 8,8 +/- 6,5
 E Nord 10,0 5,5 +/- 3,7
                       12,0 6,5 +/- 4,3
                       15,0 7,9 +/- 4,9
          Süd 10,0 6,8 +/- 5,6
                       12,0 7,3 +/- 5,2
                       15,0 8,7 +/- 6,0
 Name: aktuell, Typ: Objekt 

Die durchschnittliche Wartezeit, vielleicht ein oder zwei Minuten, beträgt mehr als die Hälfte des geplanten Intervalls, entspricht jedoch nicht dem geplanten Intervall, wie das Paradoxon der Wartezeit impliziert. Mit anderen Worten, das Inspektionsparadoxon wird bestätigt, aber das Wartezeitparadoxon ist nicht wahr.

Fazit

Das Latenzparadoxon war ein interessanter Ausgangspunkt für eine Diskussion, die Modellierung, Wahrscheinlichkeitstheorie und den Vergleich statistischer Annahmen mit der Realität umfasste. Obwohl wir bestätigt haben, dass Buslinien in der realen Welt einem Inspektionsparadoxon folgen, zeigt die obige Analyse ziemlich überzeugend: Die dem Wartezeitparadoxon zugrunde liegende Hauptannahme, dass die Ankunft von Bussen der Statistik des Poisson-Prozesses folgt, ist nicht gerechtfertigt.

Rückblickend ist dies nicht überraschend: Der Poisson-Prozess ist ein memoryloser Prozess, bei dem davon ausgegangen wird, dass die Ankunftswahrscheinlichkeit völlig unabhängig von der Zeit seit der vorherigen Ankunft ist. Tatsächlich verfügt ein gut verwaltetes öffentliches Verkehrssystem über speziell strukturierte Fahrpläne, um dieses Verhalten zu vermeiden: Busse starten ihre Routen nicht zu zufälligen Tageszeiten, sondern nach dem Zeitplan, der für den effizientesten Personenverkehr gewählt wurde.

Die wichtigere Lektion besteht darin, vorsichtig mit den Annahmen umzugehen, die Sie in Bezug auf Datenanalyse-Aufgaben treffen. Manchmal ist der Poisson-Prozess eine gute Beschreibung für Ankunftszeitdaten. Nur weil ein Datentyp wie ein anderer Datentyp klingt, bedeutet dies nicht, dass die für den einen gültigen Annahmen notwendigerweise für den anderen gültig sind. Oft können Annahmen, die richtig erscheinen, zu Schlussfolgerungen führen, die nicht wahr sind.