Vor anderthalb Jahren veröffentlichte ich den Artikel „Mathematik an den Fingern: Methoden der kleinsten Quadrate“ , der eine sehr anständige Antwort erhielt, die unter anderem darin bestand, dass ich vorschlug, eine Eule zu zeichnen. Nun, seit einer Eule musst du es noch einmal erklären. In einer Woche, genau zu diesem Thema, werde ich anfangen, geologischen Studenten mehrere Vorlesungen zu halten; Ich nutze diese Gelegenheit, ich präsentiere hier die (angepassten) Hauptpunkte als Entwurf. Mein Hauptziel ist es nicht, ein fertiges Rezept aus einem Buch über leckeres und gesundes Essen zu geben, sondern zu erklären, warum es so ist und was sonst noch im entsprechenden Abschnitt steht, weil die Verbindungen zwischen verschiedenen Abschnitten der Mathematik am interessantesten sind!

Im Moment beabsichtige ich, den Text wie folgt zu brechen:

• Bildungsprogramm zur Wahrscheinlichkeitstheorie (Einführungsartikel, optional)
  
• Einführung in lineare Gleichungssysteme
  
• Finite-Elemente-Methoden
  
• Minimierung quadratischer Formen und Beispiele für OLS-Probleme
  
• Von den kleinsten Quadraten zu neuronalen Netzen
  

Ich gehe ein wenig seitwärts zu den kleinsten Quadraten, nach dem Prinzip der maximalen Wahrscheinlichkeit, und es erfordert eine minimale Orientierung in der Wahrscheinlichkeitstheorie. Dieser Text ist für das dritte Jahr unserer Fakultät für Geologie konzipiert, was bedeutet (aus Sicht der beteiligten Ausrüstung!), Dass ein interessierter Schüler mit dem entsprechenden Eifer in der Lage sein sollte, ihn zu verstehen.

Wie gesund ist der Theoretiker oder glauben Sie an die Evolutionstheorie?

Eines Tages wurde ich gefragt, ob ich an die Evolutionstheorie glaube. Machen Sie jetzt eine Pause und überlegen Sie, wie Sie darauf antworten werden.



Persönlich war ich überrascht und antwortete, dass ich es für glaubwürdig halte und dass die Frage des Glaubens hier überhaupt nicht auftaucht. Wissenschaftliche Theorie hat wenig mit Glauben zu tun. Kurz gesagt, die Theorie baut nur ein Modell der Welt um uns herum auf, es besteht kein Grund, daran zu glauben. Darüber hinaus erfordert Poppers Kriterium eine wissenschaftliche Theorie, um widerlegt werden zu können. Und auch eine solide Theorie sollte vor allem Vorhersagekraft besitzen. Wenn Sie beispielsweise Pflanzen genetisch so verändern, dass sie selbst Pestizide produzieren, ist es nur logisch, dass gegen sie resistente Insekten auftreten. Es ist jedoch deutlich weniger offensichtlich, dass dieser Prozess verlangsamt werden kann, indem gewöhnliche Pflanzen neben gentechnisch veränderten Pflanzen wachsen. Basierend auf der Evolutionstheorie hat die entsprechende Simulation eine solche Vorhersage getroffen , und sie scheint bestätigt zu sein .

Und was haben die kleinsten Quadrate damit zu tun?

Wie ich bereits erwähnt habe, werde ich durch das Maximum-Likelihood-Prinzip zu den kleinsten Quadraten gehen. Lassen Sie uns anhand eines Beispiels veranschaulichen. Angenommen, wir interessieren uns für Daten über das Wachstum von Pinguinen, aber wir können nur einige dieser schönen Vögel messen. Es ist ziemlich logisch, ein Wachstumsverteilungsmodell in die Aufgabe einzuführen - meistens ist es normal. Die Normalverteilung ist durch zwei Parameter gekennzeichnet - Mittelwert und Standardabweichung. Für jeden festen Wert der Parameter können wir die Wahrscheinlichkeit berechnen, dass genau die von uns durchgeführten Messungen generiert werden. Durch Variieren der Parameter finden wir außerdem diejenigen, die die Wahrscheinlichkeit maximieren.

Um mit maximaler Wahrscheinlichkeit zu arbeiten, müssen wir also in Bezug auf die Wahrscheinlichkeitstheorie arbeiten. Etwas tiefer definieren wir an den Fingern das Konzept von Wahrscheinlichkeit und Wahrscheinlichkeit, aber zuerst möchte ich mich auf einen anderen Aspekt konzentrieren. Ich sehe überraschenderweise selten Menschen, die über das Wort „Theorie“ in der Phrase „Wahrscheinlichkeitstheorie“ nachdenken.

Was ist Lerntheoretiker?

In Bezug auf Herkunft, Bedeutung und Umfang der Wahrscheinlichkeitsschätzungen wird seit mehr als hundert Jahren heftig diskutiert. Zum Beispiel erklärte Bruno De Finetti , dass die Wahrscheinlichkeit nichts anderes als eine subjektive Analyse der Wahrscheinlichkeit ist, dass etwas passieren wird und dass diese Wahrscheinlichkeit nicht außerhalb des Geistes existiert. Dies ist die Bereitschaft einer Person, auf etwas zu wetten, das passiert. Diese Meinung steht in direktem Gegensatz zu der Ansicht von Klassikern / Freventisten über die Wahrscheinlichkeit eines bestimmten Ergebnisses eines Ereignisses, bei der angenommen wird, dass dasselbe Ereignis mehrmals wiederholt werden kann, und die „Wahrscheinlichkeit“ eines bestimmten Ergebnisses hängt mit der Häufigkeit zusammen, mit der ein bestimmtes Ergebnis bei wiederholten Tests ausfällt. Neben Subjektivisten und Freventisten gibt es auch Objektivisten, die argumentieren, dass Wahrscheinlichkeiten reale Aspekte des Universums sind und nicht nur Beschreibungen des Vertrauensgrades des Beobachters.

Wie dem auch sei, aber alle drei wissenschaftlichen Schulen in der Praxis verwenden denselben Apparat, der auf Kolmogorovs Axiomen basiert. Lassen Sie uns aus subjektivistischer Sicht ein indirektes Argument zugunsten der Wahrscheinlichkeitstheorie geben, die auf Kolmogorovs Axiomen beruht. Wir geben die Axiome etwas später selbst an, aber zunächst gehen wir davon aus, dass wir einen Buchmacher haben, der Wetten auf die nächste Weltmeisterschaft annimmt. Lassen Sie uns zwei Ereignisse haben: a = das Team von Uruguay wird der Champion, b = das deutsche Team wird der Champion. Der Buchmacher schätzt die Gewinnchancen des uruguayischen Teams auf 40%, die des deutschen Teams auf 30%. Natürlich können sowohl Deutschland als auch Uruguay nicht gleichzeitig gewinnen, daher ist die Chance auf a∧b Null. Gleichzeitig glaubt der Buchmacher, dass die Wahrscheinlichkeit, dass entweder Uruguay oder Deutschland (und nicht Argentinien oder Australien) gewinnen, 80% beträgt. Schreiben wir es in folgender Form:



Wenn der Buchmacher behauptet, dass sein Vertrauensgrad in Ereignis a 0,4 beträgt, dh P (a) = 0,4, kann der Spieler wählen, ob er für oder gegen das Aussprechen von a setzt , Wettbeträge, die mit dem Vertrauensgrad des Buchmachers vereinbar sind. Dies bedeutet, dass der Spieler darauf wetten kann, dass das Ereignis eintreten wird, indem er vier Rubel gegen sechs Rubel des Buchmachers setzt. Oder ein Spieler kann sechs Rubel anstelle von vier Rubel eines Buchmachers wetten, dass das Ereignis nicht stattfinden wird.

Wenn der Grad des Vertrauens des Buchmachers den Zustand der Welt nicht genau widerspiegelt, können wir uns darauf verlassen, dass er auf lange Sicht Geld an Spieler verliert, deren Überzeugungen genauer sind. Darüber hinaus hat der Spieler in diesem speziellen Beispiel eine Strategie, bei der der Buchmacher immer Geld verliert. Lassen Sie es uns veranschaulichen:



Der Spieler macht drei Wetten und gewinnt unabhängig vom Ergebnis der Meisterschaft immer. Bitte beachten Sie, dass die Berücksichtigung der Gewinne grundsätzlich nicht beinhaltet, ob Uruguay oder Deutschland die Favoriten der Meisterschaft sind, der Verlust des Buchmachers ist garantiert! Diese Situation wurde durch die Tatsache angeführt, dass der Buchmacher sich nicht von den Grundlagen der Wahrscheinlichkeitstheorie leiten ließ und gegen Kolmogorovs drittes Axiom verstieß. Lassen Sie uns alle drei bringen:



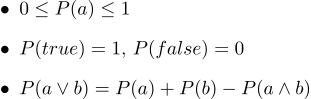
In Textform sehen sie folgendermaßen aus:

• 1. Alle Wahrscheinlichkeiten reichen von 0 bis 1
• 2. Natürlich haben wahre Aussagen eine Wahrscheinlichkeit von 1 und sicherlich eine falsche Wahrscheinlichkeit von 0.
• 3. Das dritte Axiom ist das Axiom der Disjunktion. Es ist leicht zu verstehen, wenn man feststellt, dass die Fälle, in denen die Aussage a wahr ist, zusammen mit den Fällen, in denen b wahr ist, sicherlich alle Fälle abdecken, in denen die Aussage a∨b wahr ist. In der Summe von zwei Fallmengen tritt ihr Schnittpunkt jedoch zweimal auf, weshalb P (a∧b) subtrahiert werden muss.

1931 erwies sich de Finetti als sehr starkes Statement:

Wenn sich der Buchmacher von vielen Vertrauensgraden leiten lässt, die gegen die Axiome der Wahrscheinlichkeitstheorie verstoßen, gibt es eine solche Kombination von Spielerwetten, die den Verlust des Buchmachers (Spieler gewinnt) bei jeder Wette garantiert.

Die Axiome der Wahrscheinlichkeiten können als Einschränkung der Menge probabilistischer Überzeugungen angesehen werden, die ein Agent vertreten kann. Bitte beachten Sie, dass das Befolgen des Buchmachers nicht Kolmogorovs Axiome impliziert, dass er gewinnen wird (wir werden Provisionsfragen beiseite lassen), aber wenn Sie ihnen nicht folgen, wird er garantiert verlieren. Beachten Sie, dass andere Argumente für die Anwendung von Wahrscheinlichkeiten vorgebracht wurden. Es war jedoch der praktische Erfolg von auf Wahrscheinlichkeitstheorie basierenden Argumentationssystemen, der sich als attraktiver Anreiz herausstellte, der zu einer Überarbeitung vieler Ansichten führte.

Also haben wir leicht den Schleier geöffnet, warum der Theorver vielleicht Sinn macht, aber welche Art von Objekten manipuliert er? Die gesamte Theorie basiert auf nur drei Axiomen; Alle drei beinhalten eine magische Funktion P. Wenn ich mir diese Axiome anschaue, erinnere ich mich außerdem sehr an die Formbereichsfunktion. Lassen Sie uns versuchen zu sehen, ob der Bereich funktioniert, um die Wahrscheinlichkeit zu bestimmen.

Wir definieren das Wort "Ereignis" als "Teilmenge eines Einheitsquadrats". Wir definieren das Wort "Wahrscheinlichkeit eines Ereignisses" als "Fläche der entsprechenden Teilmenge". Grob gesagt haben wir ein großes Pappziel, und nachdem wir unsere Augen geschlossen haben, schießen wir darauf. Die Wahrscheinlichkeit, dass eine Kugel in einen bestimmten Satz fällt, ist direkt proportional zur Fläche des Satzes. Ein zuverlässiges Ereignis ist in diesem Fall das gesamte Quadrat und offensichtlich falsch, zum Beispiel jeder Punkt des Quadrats. Aus unserer Definition der Wahrscheinlichkeit folgt, dass es unmöglich ist, perfekt zum Punkt zu gelangen (unsere Kugel ist ein materieller Punkt). Ich mag Bilder sehr, und ich zeichne viele davon, und Theorver ist keine Ausnahme! Lassen Sie uns alle drei Axiome veranschaulichen:



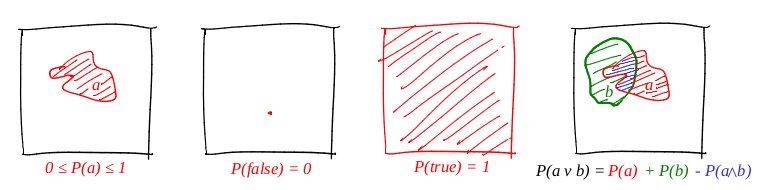
Das erste Axiom ist also erfüllt: Die Fläche ist nicht negativ und darf Einheiten nicht überschreiten. Ein zuverlässiges Ereignis ist das ganze Quadrat, und ein absichtlich falsches ist jede Menge von Nullflächen. Und es funktioniert perfekt mit dem Disjunkt!

Maximale Glaubwürdigkeit mit Beispielen

Beispiel Eins: Münzwurf

Schauen wir uns das einfachste Beispiel eines Münzwurfs an, auch bekannt als Bernoullis Schema . Es werden N Experimente durchgeführt, bei denen jeweils eines von zwei Ereignissen auftreten kann ("Erfolg" oder "Misserfolg"), eines mit der Wahrscheinlichkeit p und das zweite mit der Wahrscheinlichkeit 1-p . Unsere Aufgabe ist es, die Wahrscheinlichkeit zu finden, in diesen n Experimenten genau k Erfolge zu erzielen . Diese Wahrscheinlichkeit gibt uns die Bernoulli-Formel:



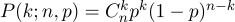
Nehmen Sie eine gewöhnliche Münze ( p = 0,5 ), werfen Sie sie zehnmal ( n = 10 ) und überlegen Sie, wie oft die Schwänze fallen gelassen werden:



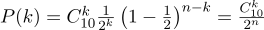
Hier ist ein Diagramm der Wahrscheinlichkeitsdichte:



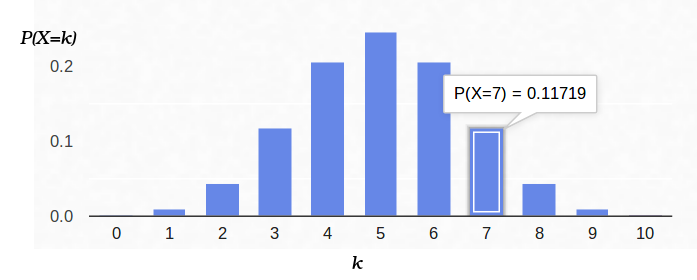
Wenn wir also die Wahrscheinlichkeit des Beginns des „Erfolgs“ (0,5) und auch die Anzahl der Experimente (10) festlegen, kann die mögliche Anzahl der „Erfolge“ eine beliebige Ganzzahl zwischen 0 und 10 sein. Diese Ergebnisse sind jedoch nicht gleich wahrscheinlich. Es ist offensichtlich, dass fünf "Erfolge" viel wahrscheinlicher sind als kein einziger. Zum Beispiel beträgt die Wahrscheinlichkeit, sieben Schwänze zu zählen, ungefähr 12%.

Betrachten wir nun dieselbe Aufgabe von der anderen Seite. Wir haben eine echte Münze, aber wir kennen ihre Verteilung der a priori-Wahrscheinlichkeit „Erfolg“ / „Misserfolg“ nicht. Wir können es jedoch zehnmal werfen und die Anzahl der „Erfolge“ zählen. Zum Beispiel haben wir sieben Schwänze. Wie hilft uns dies, p zu bewerten?

Wir können versuchen, n = 10 und k = 7 in der Bernoulli-Formel zu fixieren, wobei p ein freier Parameter bleibt:



Dann kann die Bernoulli-Formel als die Wahrscheinlichkeit des geschätzten Parameters interpretiert werden (in diesem Fall p ). Ich habe sogar den Buchstaben der Funktion geändert, jetzt ist es L (von der englischen Ähnlichkeit). Das heißt, die Wahrscheinlichkeit ist die Wahrscheinlichkeit, Beobachtungsdaten (7 Schwänze aus 10 Experimenten) für einen gegebenen Wert des Parameters (der Parameter) zu erzeugen.

Beispielsweise beträgt die Wahrscheinlichkeit einer ausgeglichenen Münze ( p = 0,5), vorausgesetzt, dass sieben von zehn Würfen auftreten, ungefähr 12%. Sie können die Funktion L zeichnen:



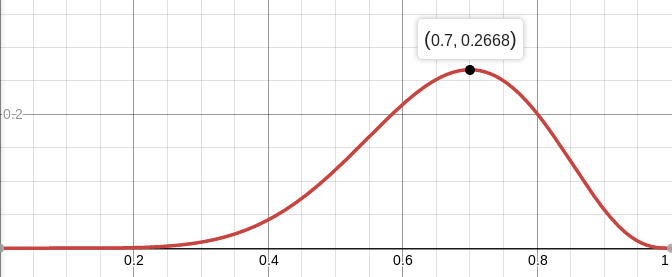
Wir suchen daher nach einem Wert von Parametern, der die Wahrscheinlichkeit maximiert, die Beobachtungen zu erhalten, die wir haben. In diesem speziellen Fall haben wir eine Funktion einer Variablen, wir suchen nach ihrem Maximum. Um die Suche zu vereinfachen, suche ich maximal L , sondern log L. Der Logarithmus ist eine streng monotone Funktion, daher ist das Maximieren des einen und des anderen genau dasselbe. Und der Logarithmus zerlegt das Produkt in eine Menge, die viel bequemer zu unterscheiden ist. Wir suchen also das Maximum dieser Funktion:



Dazu setzen wir seine Ableitung mit Null gleich:



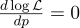
Die Ableitung von log x = 1 / x erhalten wir:



Das heißt, die maximale Wahrscheinlichkeit (ungefähr 27%) wird bei erreicht



Für alle Fälle berechnen wir die zweite Ableitung:



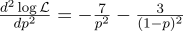
Am Punkt p = 0,7 ist es negativ, also ist dieser Punkt wirklich das Maximum der Funktion L.



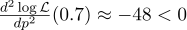
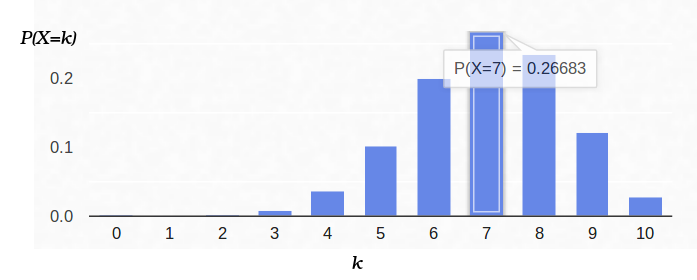
Und hier ist die Wahrscheinlichkeitsdichte für das Bernoulli-Schema mit p = 0,7:

Beispiel Zwei: ADC

Stellen wir uns vor, wir haben eine bestimmte konstante physikalische Größe, die wir messen möchten, sei es eine Länge mit einem Lineal oder eine Spannung mit einem Voltmeter. Jede Messung gibt eine Annäherung an diese Größe, jedoch nicht an die Menge selbst. Die Methoden, die ich hier beschreibe, wurden von Gauß Ende des 18. Jahrhunderts entwickelt, als er die Umlaufbahnen von Himmelskörpern maß.

Wenn wir zum Beispiel die Batteriespannung N-mal messen, erhalten wir N verschiedene Messungen. Welches soll ich nehmen? Das ist alles! Lassen Sie uns also N Mengen Uj haben:



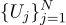
Angenommen, jede Messung Uj entspricht einem idealen Wert plus einem Gaußschen Rauschen, das durch zwei Parameter gekennzeichnet ist - die Position der Gaußschen Glocke und ihre „Breite“. Hier ist die Wahrscheinlichkeitsdichte:



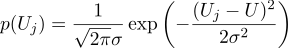
Das heißt, wenn N Werte von Uj gegeben sind, besteht unsere Aufgabe darin, einen solchen Parameter U zu finden, der den Wahrscheinlichkeitswert maximiert. Glaubwürdigkeit (ich nehme sofort den Logarithmus daraus) kann wie folgt geschrieben werden:



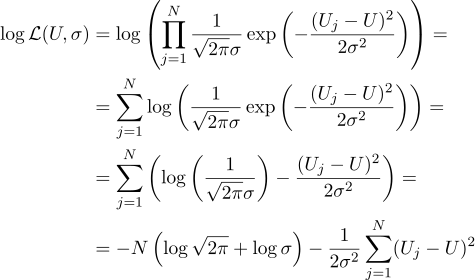
Nun, dann ist alles streng wie zuvor, wir setzen in Bezug auf die Parameter, nach denen wir suchen, null partielle Ableitungen gleich:



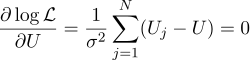
Wir finden, dass die wahrscheinlichste Schätzung der unbekannten Größe U als Durchschnitt aller Messungen gefunden werden kann:



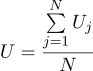
Nun, der wahrscheinlichste Sigma-Parameter ist die übliche Standardabweichung:




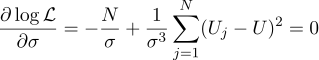
Hat es sich gelohnt, einen einfachen Durchschnitt aller Messungen in der Antwort zu erhalten? Für meinen Geschmack hat es sich gelohnt. Übrigens ist es eine Standardpraxis, mehrere Messungen mit einem konstanten Wert zu mitteln, um die Genauigkeit der Messungen zu erhöhen. Zum Beispiel ADC-Mittelwertbildung . Übrigens, für dieses Gaußsche Rauschen ist es nicht notwendig, dass das Rauschen unverzerrt ist.

Beispiel drei und wieder eindimensional

Wir setzen das Gespräch fort, nehmen wir das gleiche Beispiel, erschweren es aber ein wenig. Wir wollen den Widerstand eines bestimmten Widerstands messen. Mit Hilfe eines Labornetzteils können wir eine Standardamperezahl durchlassen und die dafür benötigte Spannung messen. Das heißt, wir haben N Zahlenpaare (Ij, Uj) am Eingang unseres Widerstandsbewerters.



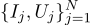
Zeichnen Sie diese Punkte auf das Diagramm. Das Ohmsche Gesetz sagt uns, dass wir nach der Steigung der blauen Linie suchen.



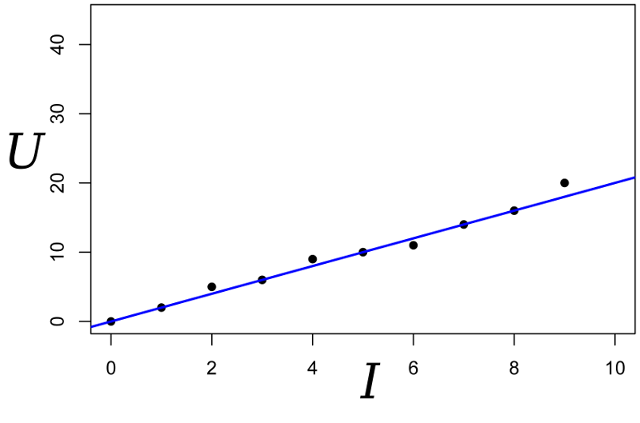
Wir schreiben den Ausdruck für die Wahrscheinlichkeit des Parameters R:



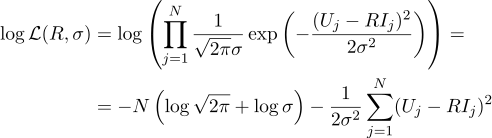
Und wieder setzen wir die entsprechende partielle Ableitung auf Null:



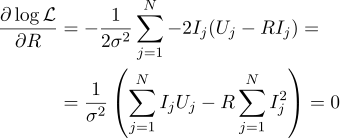
Dann kann der plausibelste Widerstand R durch die folgende Formel gefunden werden:



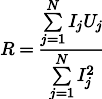
Dieses Ergebnis ist bereits etwas weniger offensichtlich als der einfache Durchschnitt aller Messungen. Bitte beachten Sie, dass wenn wir hundert Messungen im Bereich von einem Ampere und eine Messung im Bereich von einem Kiloampere durchführen, die vorherigen hundert Messungen das Ergebnis praktisch nicht beeinflussen. Erinnern wir uns an diese Tatsache, sie wird uns im nächsten Artikel nützlich sein.

Viertes Beispiel: Zurück zu den kleinsten Quadraten

Sicherlich haben Sie bereits bemerkt, dass in den letzten beiden Beispielen die Maximierung des Wahrscheinlichkeitslogarithmus der Minimierung der Summe der Quadrate des Schätzfehlers entspricht. Schauen wir uns ein anderes Beispiel an. Nehmen Sie die Kalibrierung des Steelyards anhand von Referenzgewichten vor. Angenommen, wir haben N Referenzlasten der Masse xj, hängen sie an einen Stahlhof und messen die Länge der Feder. Wir erhalten N Federlängen yj:



Das Hookesche Gesetz besagt, dass die Ausdehnung der Feder linear von der ausgeübten Kraft abhängt und diese Kraft das Gewicht der Ware und das Gewicht der Feder selbst umfasst. Die Federsteifigkeit sei der Parameter a , aber die Federspannung unter ihrem eigenen Gewicht ist der Parameter b. Dann können wir den Ausdruck der Wahrscheinlichkeit unserer Messungen auf diese Weise schreiben (wie zuvor unter der Hypothese des Gaußschen Messrauschens):



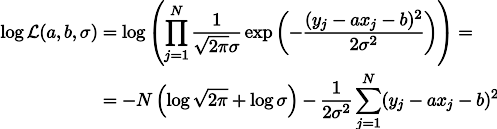
Die Wahrscheinlichkeitsmaximierung von L entspricht der Minimierung der Summe der Quadrate der Schätzfehler, dh wir können nach dem Minimum der Funktion S suchen, die wie folgt definiert ist:



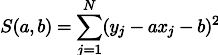
Mit anderen Worten, wir suchen nach einer geraden Linie, die die Summe der Quadrate der Längen der grünen Segmente minimiert:



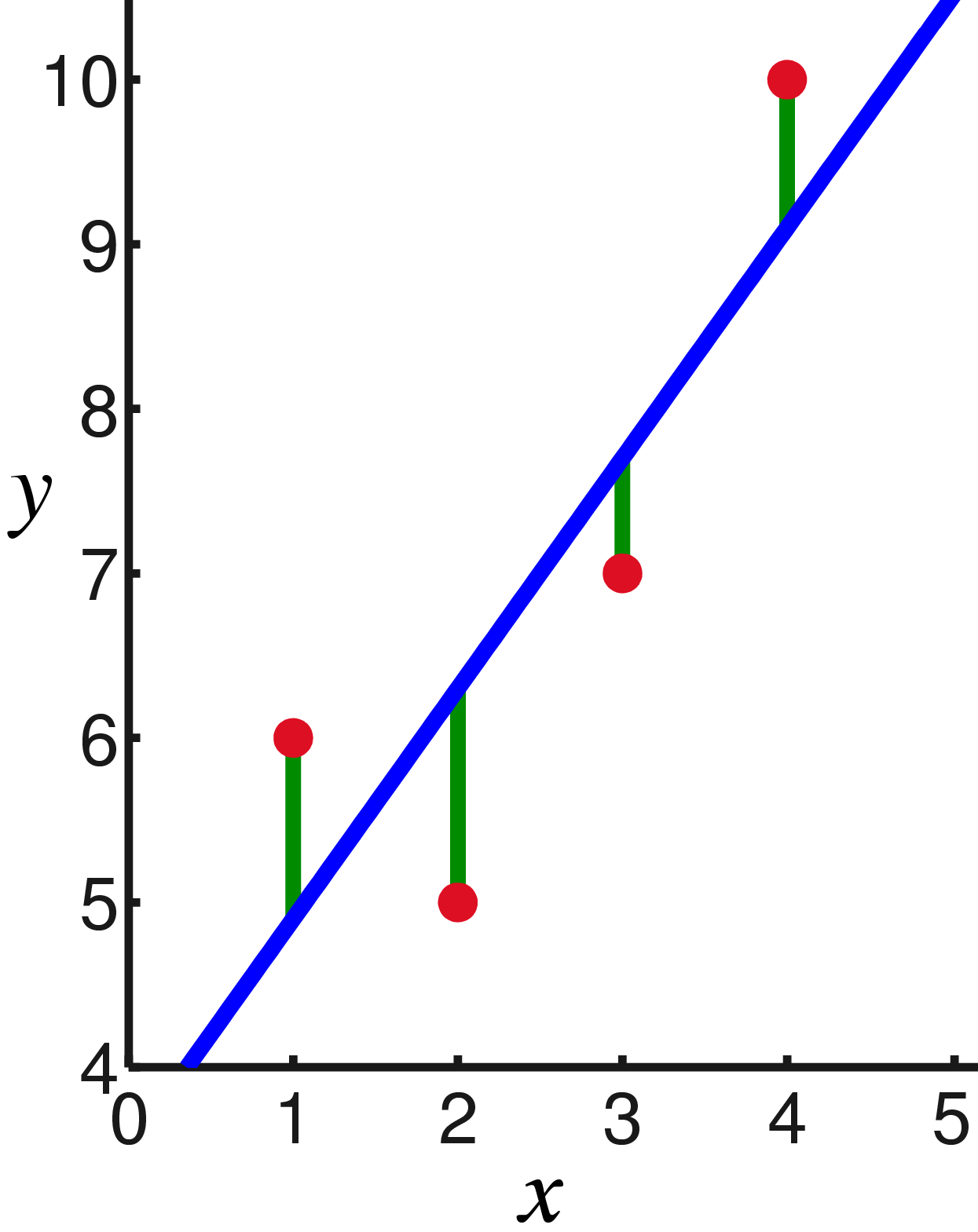
Nun, dann keine Überraschungen, wir setzen partielle Ableitungen auf Null:



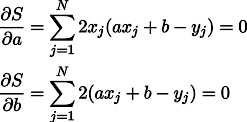
Wir erhalten ein System aus zwei linearen Gleichungen mit zwei Unbekannten:



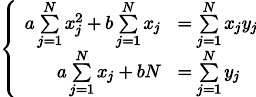
Wir erinnern uns an die siebte Klasse der Schule und schreiben die Lösung auf:

Fazit

Least-Square-Methoden sind ein Sonderfall zur Maximierung der Wahrscheinlichkeit für Fälle, in denen die Wahrscheinlichkeitsdichte Gaußsch ist. In dem Fall, in dem die Dichte (überhaupt nicht) Gaußsch ist, ergeben die kleinsten Quadrate eine Schätzung, die sich von der MLE (Maximum Likehood Estimation) unterscheidet. Übrigens stellte Gauß einmal die Hypothese auf, dass die Verteilung keine Rolle spielt, sondern nur die Unabhängigkeit der Tests wichtig ist.

Wie Sie diesem Artikel entnehmen können, sind die analytischen Lösungen für dieses Problem umso umständlicher, je weiter Sie in den Wald vordringen. Nun ja, wir sind nicht im achtzehnten Jahrhundert, wir haben Computer! Das nächste Mal werden wir eine geometrische und dann eine programmatische Herangehensweise an das Problem von OLS sehen, bleiben Sie auf dem Laufenden.