Ich habe mich lange vorbereitet und Material gesammelt, ich hoffe, diesmal ist es besser geworden. Ich widme diesen Artikel den grundlegenden Methoden zur Lösung mathematischer Optimierungsprobleme mit Einschränkungen. Wenn Sie also gehört haben, dass die Simplex-Methode eine
sehr wichtige Methode ist, aber immer noch nicht wissen, was sie bewirkt, wird Ihnen dieser Artikel wahrscheinlich helfen.
PS Der Artikel enthält mathematische Formeln, die vom Makro-Editor hinzugefügt wurden. Sie sagen, dass sie manchmal nicht angezeigt werden. Es gibt auch viele Animationen im GIF-Format.
Präambel
Das Problem der mathematischen Optimierung ist ein Problem der Form „Find in the set
mathcalK das Element
x∗ so dass für alle
x von
mathcalK durchgeführt
f(x∗) leqf(x) ", Was in der wissenschaftlichen Literatur wahrscheinlich so etwas geschrieben ist
\ begin {array} {rl} \ mbox {minimieren} & f (x) \\ \ mbox {bereitgestellt} & x \ in \ mathcal {K}. \ end {array}
\ begin {array} {rl} \ mbox {minimieren} & f (x) \\ \ mbox {bereitgestellt} & x \ in \ mathcal {K}. \ end {array}
Historisch gesehen funktionieren beliebte Methoden wie der Gradientenabstieg oder die Newtonsche Methode nur in linearen Räumen (und vorzugsweise beispielsweise in einfachen)
mathbbRn ) In der Praxis gibt es häufig Probleme, bei denen Sie ein Minimum finden müssen, das nicht im linearen Raum liegt. Zum Beispiel müssen Sie das Minimum einer Funktion für solche Vektoren finden
x=(x1, ldots,xn) für welche
xi geq0 Dies kann daran liegen, dass
xi bezeichnen die Längen von Objekten. Oder zum Beispiel, wenn
x Stellen Sie die Koordinaten eines Punktes dar, der nicht größer als sein sollte
r von
y d.h.
|x−y | leqr . Für solche Probleme ist der Gradientenabstieg oder die Newton-Methode nicht mehr direkt anwendbar. Es stellte sich heraus, dass eine sehr große Klasse von Optimierungsproblemen zweckmäßigerweise durch „Einschränkungen“ abgedeckt ist, ähnlich den oben beschriebenen. Mit anderen Worten ist es zweckmäßig, die Menge darzustellen
mathcalK in Form eines Systems von Gleichheiten und Ungleichheiten
beginarraylgi(x) leq0, 1 leqi leqm,hi(x)=0, 1 leqi leqk. endarray
Minimierungsprobleme über einen Bereich des Formulars
mathbbRn Daher nannten sie sie willkürlich "uneingeschränktes Problem" und Probleme über Mengen, die durch Mengen von Gleichheiten und Ungleichheiten definiert sind - "beschränkte Probleme".
Technisch absolut jede Menge
mathcalK kann als einzelne Gleichheit oder Ungleichung unter Verwendung der
Indikatorfunktion dargestellt werden , die definiert ist als
I_ \ mathcal {K} (x) = \ begin {Fälle} 0, & x \ notin \ mathcal {K} \\ 1, & x \ in \ mathcal {K}, \ end {Fälle}
Eine solche Funktion hat jedoch keine verschiedenen nützlichen Eigenschaften (Konvexität, Differenzierbarkeit usw.). Man kann sich jedoch oft vorstellen
mathcalK in Form mehrerer Gleichheiten und Ungleichungen, von denen jede solche Eigenschaften hat. Die Grundtheorie wird unter dem Fall zusammengefasst
\ begin {array} {rl} \ mbox {minimieren} & f (x) \\ \ mbox {bereitgestellt} & g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ end {array}
wo
f,gi - konvexe (aber nicht unbedingt differenzierbare) Funktionen,
A - Matrix. Um zu demonstrieren, wie die Methoden funktionieren, werde ich zwei Beispiele verwenden:
- Lineare Programmieraufgabe
$$ display $$ \ begin {array} {rl} \ mbox {minimieren} & -2 & x ~~~ - & y \\ \ mbox {bereitgestellt} & -1.0 & ~ x -0.1 & ~ y \ leq -1.0 \ \ & -1,0 & ~ x + ~ 0,6 & ~ y \ leq -1,0 \\ & -0,2 & ~ x + ~ 1,5 & ~ y \ leq -0,2 \\ & ~ 0,7 & ~ x + ~ 0,7 & ~ y \ leq 0,7 \\ & ~ 2,0 & ~ x -0,2 & ~ y \ leq 2,0 \\ & ~ 0,5 & ~ x -1,0 & ~ y \ leq 0,5 \\ & -1,0 & ~ x -1,5 & ~ y \ leq - 1.0 \\ \ end {array} $$ display $$
Im Wesentlichen besteht dieses Problem darin, den am weitesten entfernten Punkt des Polygons in der Richtung (2, 1) zu finden. Die Lösung des Problems ist der Punkt (4.7, 3.5) - der „richtigste“ im Polygon. Aber das Polygon selbst

- Minimierung einer quadratischen Funktion mit einer quadratischen Bedingung
\ begin {array} {rl} \ mbox {minimieren} & 0,7 (x - y) ^ 2 + 0,1 (x + y) ^ 2 \\ \ mbox {bereitgestellt} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {array}
Simplex-Methode
Von allen Methoden, die ich in diesem Test behandele, ist die Simplex-Methode wahrscheinlich die bekannteste. Die Methode wurde speziell für die lineare Programmierung entwickelt und ist die einzige, die in einer endlichen Anzahl von Schritten die exakte Lösung erreicht (vorausgesetzt, die exakte Arithmetik wird für Berechnungen verwendet, in der Praxis ist dies normalerweise nicht der Fall, aber theoretisch ist dies möglich). Die Idee einer Simplex-Methode besteht aus zwei Teilen:
- Systeme linearer Ungleichungen und Gleichheiten definieren mehrdimensionale konvexe Polyeder (Polytope). Im eindimensionalen Fall ist dies ein Punkt, ein Strahl oder ein Segment, im zweidimensionalen Fall ein konvexes Polygon, im dreidimensionalen Fall ein konvexes Polyeder. Das Minimieren der linearen Funktion bedeutet im Wesentlichen, den „am weitesten entfernten“ Punkt in einer bestimmten Richtung zu finden. Ich denke, die Intuition sollte darauf hinweisen, dass dieser am weitesten entfernte Punkt ein bestimmter Höhepunkt sein sollte, und das ist in der Tat so. Im Allgemeinen für ein System aus m Ungleichungen in n -dimensionaler Raum Ein Scheitelpunkt ist ein Punkt, der ein System erfüllt, für das genau n aus diesen Ungleichungen werden Gleichheiten (vorausgesetzt, unter den Ungleichungen gibt es keine Äquivalente). Es gibt immer eine begrenzte Anzahl solcher Punkte, obwohl es viele davon geben kann.
- Jetzt haben wir eine endliche Menge von Punkten. Im Allgemeinen können Sie sie einfach auswählen und sortieren, dh so etwas tun: für jede Teilmenge von n Ungleichungen, lösen Sie das System linearer Gleichungen, das aus den gewählten Ungleichungen zusammengestellt wurde, überprüfen Sie, ob die Lösung zum ursprünglichen Ungleichungssystem passt, und vergleichen Sie sie mit anderen solchen Punkten. Dies ist eine ziemlich einfache ineffiziente, aber funktionierende Methode. Die Simplex-Methode bewegt sich anstelle der Iteration entlang der Kanten von oben nach oben, sodass sich die Werte der Zielfunktion verbessern. Es stellt sich heraus, dass ein Scheitelpunkt, der keine „Nachbarn“ hat, in denen die Werte der Funktion besser sind, optimal ist.
Die Simplex-Methode ist iterativ, dh sie verbessert die Lösung nacheinander geringfügig. Für solche Methoden müssen Sie irgendwo beginnen, im allgemeinen Fall erfolgt dies durch Lösen eines Hilfsproblems
\ begin {array} {rl} \ mbox {minimieren} & s \\ \ mbox {bereitgestellt} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
Wenn, um dieses Problem zu lösen
x∗,s∗ so dass
s∗ leq0 dann ausgeführt
gi(x∗) leqs leq0 Andernfalls wird das ursprüngliche Problem im Allgemeinen auf einem leeren Satz angegeben. Um das Hilfsproblem zu lösen, können Sie auch die Simplex-Methode verwenden, aber der Ausgangspunkt kann genommen werden
s= maxigi(x) mit willkürlich
x . Das Finden des Startpunkts kann willkürlich als die erste Phase des Verfahrens bezeichnet werden, das Finden der Lösung für das ursprüngliche Problem kann willkürlich als die zweite Phase des Verfahrens bezeichnet werden.
Die Flugbahn der Zwei-Phasen-Simplex-MethodeDie Trajektorie wurde mit scipy.optimize.linprog generiert.
Projektiver Gradientenabstieg
Über den Gradientenabstieg habe ich kürzlich einen separaten
Artikel geschrieben, in dem ich diese Methode auch kurz beschrieben habe. Jetzt ist diese Methode ziemlich lebhaft, wird aber im Rahmen eines allgemeineren
proximalen Gradientenabfalls untersucht . Die Idee der Methode ist ziemlich banal: Wenn wir einen Gradientenabstieg auf eine konvexe Funktion anwenden
f Dann erhalten wir mit der richtigen Auswahl der Parameter ein globales Minimum
f . Wenn nach jedem Schritt des Gradientenabfalls der erhaltene Punkt korrigiert wird, wird stattdessen seine Projektion auf eine geschlossene konvexe Menge vorgenommen
mathcalK Als Ergebnis erhalten wir das Minimum der Funktion
f auf
mathcalK . Nun, oder formal gesehen, ist der projektive Gradientenabstieg ein Algorithmus, der sequentiell berechnet
beginFällexk+1=yk− alphak nablaf(yk)yk+1=P mathcalK(xk+1), EndeFälle
wo
P mathcalK(x)= mboxargminy in mathcalK |x−y |.
Die letzte Gleichheit definiert den Standardoperator der Projektion auf die Menge, tatsächlich ist es eine Funktion, die gemäß dem Punkt
x berechnet den nächstgelegenen Punkt zur Menge
mathcalK . Hier spielt die Rolle der Distanz
| ldots | Es ist erwähnenswert, dass hier jede
Norm verwendet werden kann. Projektionen mit unterschiedlichen Normen können jedoch unterschiedlich sein!
In der Praxis wird der projektive Gradientenabstieg nur in besonderen Fällen verwendet. Das Hauptproblem besteht darin, dass die Berechnung der Projektion noch schwieriger sein kann als die ursprüngliche, und sie muss viele Male berechnet werden. Der häufigste Fall, für den es zweckmäßig ist, einen projektiven Gradientenabstieg zu verwenden, sind "Box-Einschränkungen", die die Form haben
elli leqxi leqri, 1 leqi leqn.
In diesem Fall wird die Projektion für jede Koordinate sehr einfach berechnet
[P _ {\ mathcal {K}} (x)] _ i = \ begin {Fälle} r_i, & x_i> r_i \\ \ ell_i, & x_i <\ ell_i \\ x_i, & x_i \ in [\ ell_i, r_i ]. \ end {Fälle}
Die Verwendung des projektiven Gradientenabfalls für lineare Programmierprobleme ist völlig bedeutungslos. Wenn Sie dies jedoch tun, sieht es ungefähr so aus
Projektive Gradientenabstiegstrajektorie für ein lineares Programmierproblem Und hier ist die Flugbahn des projektiven Gradientenabfalls für das zweite Problem, wenn
Wählen Sie eine große Schrittweite und wenn
Wählen Sie eine kleine Schrittgröße Ellipsoid-Methode
Diese Methode ist insofern bemerkenswert, als sie der erste Polynomalgorithmus für lineare Programmierprobleme ist und als mehrdimensionale Verallgemeinerung
der Halbierungsmethode angesehen werden kann . Ich werde mit einer allgemeineren
Methode zum Trennen der Hyperebene beginnen :
- Bei jedem Schritt der Methode gibt es einen Satz, der die Lösung des Problems enthält.
- Bei jedem Schritt wird eine Hyperebene erstellt, wonach alle Punkte, die auf einer Seite der ausgewählten Hyperebene liegen, aus der Menge entfernt werden und einige neue Punkte zu dieser Menge hinzugefügt werden können
Bei Optimierungsproblemen basiert die Konstruktion der "trennenden Hyperebene" auf der folgenden Ungleichung für konvexe Funktionen
f(y) geqf(x)+ nablaf(x)T(y−x).
Wenn behoben
x dann für eine konvexe Funktion
f halber Raum
nablaf(x)T(y−x) geq0 enthält nur Punkte mit einem Wert, der nicht kleiner als an einem Punkt ist
x Das heißt, sie können abgeschnitten werden, da diese Punkte nicht besser sind als die, die wir bereits gefunden haben. Bei Problemen mit Einschränkungen können Sie auch Punkte entfernen, die garantiert gegen eine der Einschränkungen verstoßen.
Die einfachste Version der Methode zum Trennen von Hyperebenen besteht darin, einfach Halbräume abzuschneiden, ohne Punkte hinzuzufügen. Infolgedessen haben wir bei jedem Schritt ein bestimmtes Polyeder. Das Problem bei diesem Verfahren besteht darin, dass die Anzahl der Flächen des Polyeders wahrscheinlich von Schritt zu Schritt zunimmt. Darüber hinaus kann es exponentiell wachsen.
Die Ellipsoidmethode speichert tatsächlich bei jedem Schritt ein Ellipsoid. Genauer gesagt wird nach dem Aufbau der Hyperebene ein Ellipsoid mit minimalem Volumen konstruiert, das einen der Teile des Originals enthält. Dies kann durch Hinzufügen neuer Punkte erreicht werden. Ein Ellipsoid kann immer wie folgt durch eine positive bestimmte Matrix und einen Vektor (Zentrum eines Ellipsoids) definiert werden
\ mathcal {E} (P, x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}.
Die Konstruktion eines minimalen Ellipsoids im Volumen, das den Schnittpunkt des Halbraums und eines anderen Ellipsoids enthält, kann unter Verwendung von
mäßig umständlichen Formeln erfolgen . Leider war diese Methode in der Praxis immer noch so gut wie die Simplex-Methode oder die interne Punktmethode.
Aber eigentlich wie es funktioniert
und für
quadratische Programmierung Inside Point-Methode
Diese Methode hat eine lange Entwicklungsgeschichte. Eine der ersten Voraussetzungen trat ungefähr zur gleichen Zeit auf, als die Simplex-Methode entwickelt wurde. Zu diesem Zeitpunkt war es jedoch noch nicht effektiv genug, um in der Praxis eingesetzt zu werden. Später im Jahr 1984 wurde eine
Variante der Methode speziell für die lineare Programmierung entwickelt, die sowohl in der Theorie als auch in der Praxis gut war. Darüber hinaus ist die interne Punktmethode im Gegensatz zur Simplex-Methode nicht nur auf die lineare Programmierung beschränkt, sondern jetzt der Hauptalgorithmus für konvexe Optimierungsprobleme mit Einschränkungen.
Die Grundidee der Methode besteht darin, die Beschränkungen durch eine Geldbuße in Form der sogenannten
Barrierefunktion zu ersetzen. Funktion
F:Int mathcalK rightarrow mathbbR die
Barrierefunktion für das Set genannt
mathcalK wenn
F(x) rightarrow+ infty mboxatx rightarrow teilweise mathcalK.
Hier
Int mathcalK - innen
mathcalK ,
teilweise mathcalK - Grenze
mathcalK . Anstelle des ursprünglichen Problems wird vorgeschlagen, das Problem zu lösen
mboxMinimierenumx varphi(x,t)=tf(x)+F(x).
F und
varphi nur auf der Innenseite gegeben
mathcalK (Tatsächlich kommt hier der Name her), die Eigenschaft der Barriere stellt dies sicher
varphi Zumindest
x existiert. Darüber hinaus desto mehr
t Je größer die Wirkung
f . Unter vernünftigen Bedingungen können Sie dies erreichen, wenn Sie zielen
t bis unendlich dann das Minimum
varphi wird zur Lösung des ursprünglichen Problems konvergieren.
Wenn das Set
mathcalK als eine Reihe von Ungleichungen gegeben
gi(x) leq0, 1 leqi leqm dann ist die Standardwahl der Barrierefunktion die
logarithmische BarriereF(x)=− summi=1 ln(−gi(x)).
Mindestpunkte
x∗(t) die Funktionen
varphi(x,t) für anders
t bildet eine Kurve, die üblicherweise als
zentraler Pfad bezeichnet wird. Die innere Punktmethode versucht sozusagen, diesem Pfad zu folgen. So sieht es aus
Beispiele für lineare Programmierung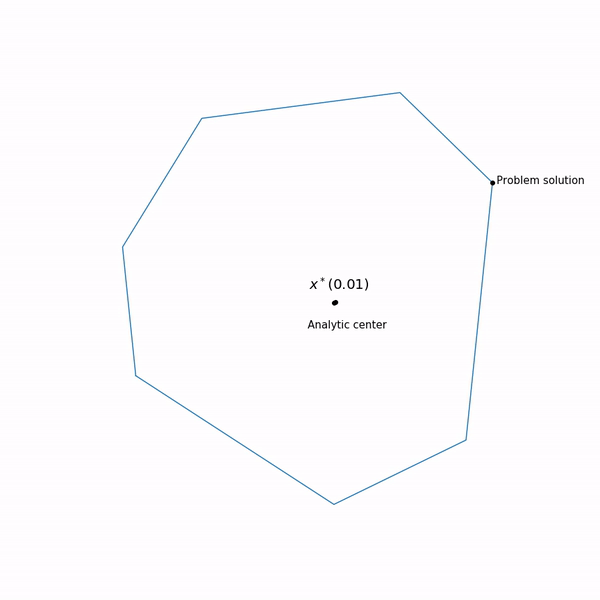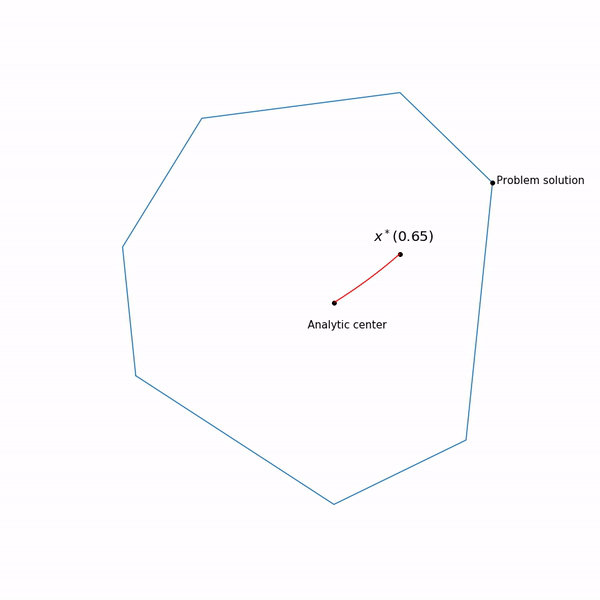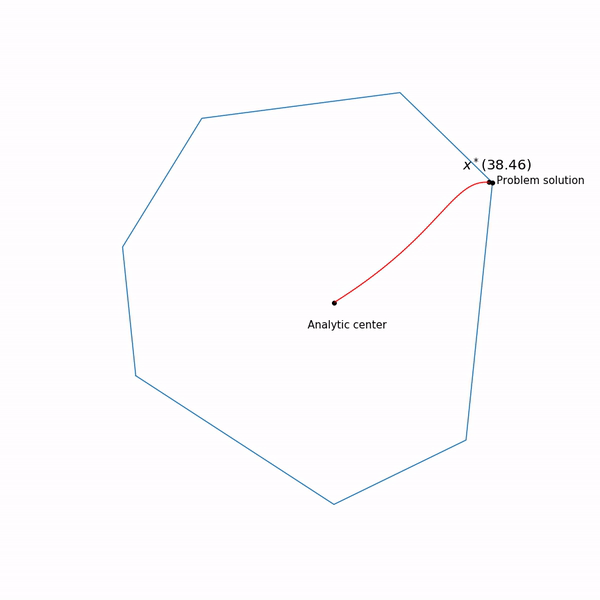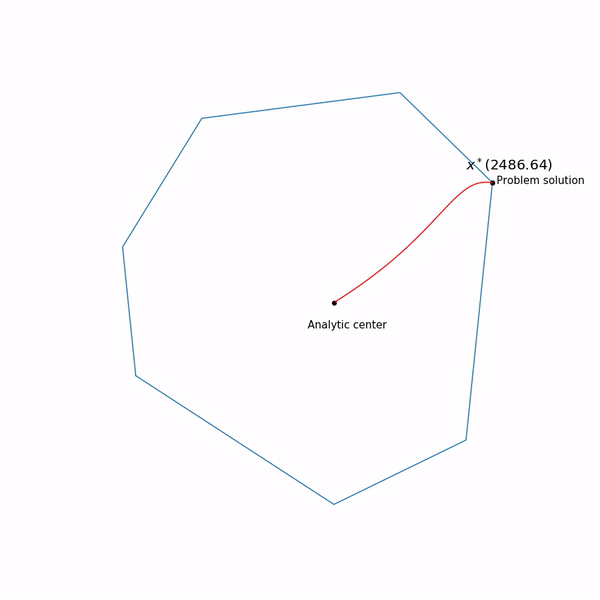 Das Analysezentrum
Das Analysezentrum ist gerecht
x∗(0) Schließlich hat die interne Punktmethode selbst die folgende Form
- Wählen Sie eine anfängliche Annäherung x0 , t0>0
- Wählen Sie eine neue Näherung mit der Newton-Methode
xk+1=xk−[ nabla2x varphi(xk,tk)]−1 nablax varphi(xk,tk)
- Zum Vergrößern anklicken t
tk+1= alphatk, alpha>1
Die Verwendung der Newton-Methode ist hier sehr wichtig: Tatsache ist, dass mit der richtigen Wahl der Barrierefunktion der Schritt der Newton-Methode einen Punkt erzeugt
, der innerhalb unserer Menge bleibt , wir haben experimentiert, er gibt nicht immer in dieser Form aus. Und schließlich die Flugbahn der internen Punktmethode
Lineare ProgrammieraufgabeDer springende schwarze Punkt ist
x∗(tk) d.h. Punkt, zu dem wir versuchen, uns dem Schritt der Newton-Methode im aktuellen Schritt zu nähern.
Quadratisches Programmierproblem