Im Jahr 2018 haben wir drei Yandex.Blitz-Wettbewerbe durchgeführt - in den Bereichen maschinelles Lernen, mobile Entwicklung und Frontend. Der dritte Wettbewerb fand kürzlich statt - Glückwunsch an die Gewinner! In der Zwischenzeit möchten wir zum zweiten zurückkehren, wo Aufgaben an der Schnittstelle von Algorithmen und Schreibsoftware für Android / iOS vorgeschlagen wurden. Kandidaten für die Position eines mobilen Entwicklers in Yandex profitieren von der Erfahrung bei der Lösung solcher Probleme. Lesen Sie die detaillierte Analyse einiger von ihnen. Und wenn Sie nicht am Blitz teilgenommen haben, ist es besser, zuerst zu versuchen , sie selbst zu lösen .

Die Aufgabe der "Gasversorgung"
| Geben Sie ein | Fazit | Zeitlimit | Speicherlimit |
|---|
| Standardeingabe oder input.txt | Standardausgabe oder output.txt | 15 Sekunden | 15 Megabyte |
Nika entwickelt eine Anwendung für Top-Manager eines großen Gasunternehmens, um sie bei der Planung der Produktion zu unterstützen.
Das Unternehmen erwägt n Felder, die d 1 ... d i ... d n Kilometer von der Pipeline entfernt sind und v 1 ... v i ... v n Gaseinheiten produzieren können. Für jedes Feld wird eine separate Lizenz verkauft - Lizenzen sind s 1 ... s i ... s n .
Um die Felder mit der Autobahn zu verbinden, müssen Sie Pipelines bauen. Ein Auftragnehmer, der m verschiedene Rohrtypen verlegen kann, hilft diesem Unternehmen. Rohre unterscheiden sich in Länge (l 1 ... l i ... l m ) und Preis (p 1 ... p i ... p m ). Sie können nach Belieben miteinander kombiniert werden.
Das Unternehmen hat k Münzen und möchte so viel Benzin wie möglich bekommen.
Wie viel kann das Unternehmen produzieren, wenn es dem Auftragnehmer optimale Aufträge erteilt?
Die Pipeline kann länger sein als der Abstand vom Feld zur Pipeline.
Die erste Zeile enthält eine ganze Zahl k ≤ 10 5 .
Die zweite Zeile enthält eine ganze Zahl n ≤ 15.
Die nächsten n Zeilen enthalten drei ganze Zahlen d i ≤ 100, v i ≤ 100 und s i ≤ 100.
Die Zahlen sind durch ein Leerzeichen getrennt.
Die nächste Zeile enthält eine ganze Zahl m ≤ 15.
Die nächsten m Zeilen enthalten zwei ganze Zahlen l i ≤ 100 und p i ≤ 100. Die Zahlen sind durch ein Leerzeichen getrennt.
Die einzige Zeile mit der Antwort.
Beispiele
| Geben Sie ein | Fazit |
116
3
58 7 50
81 71 56
52 57 31
3
47 9
1 25
18 61 | 57 |
Parsen
Definieren wir zunächst die Notation. Es gebe eine Klasse von Objekten Einzahlung (Einzahlung) mit Parametern $ inline $ Dd_ {i} $ inline $ (Abgeschiedenheit) $ inline $ Dv_ {i} $ inline $ (Produktionsvolumen) und $ inline $ Ds_ {i} $ inline $ (Lizenzkosten). Indexobjekte dieses Typs sind die Variablen i. Es gibt auch eine Pipeliner-Objektklasse mit Parametern $ inline $ PPl_ {j} $ inline $ (die Länge des Rohrs, das der Auftragnehmer bauen kann) und $ inline $ PPp_ {j} $ inline $ (Preis dieser Pfeife), Index bis j. Die Teilnehmer des Blitzes fragten oft, ob ein Pfeifentyp zweimal verwendet werden könne. Es wird angenommen, dass nein, und dieses Beispiel zeigt deutlich. Also durch die Bedingungen dieser Aufgabe zu akzeptieren $ inline $ D_ {i} = {0, 1} $ inline $ (Wählen Sie ein Feld oder nicht) und $ inline $ PP_ {j} = {0, 1} $ inline $ (Wählen Sie einen Auftragnehmer oder nicht), können Sie eine lineare Programmieraufgabe ausführen:
$ inline $ \ sum \ limit_ {i} D_ {i} * Dv_ {i} \ rightarrow max \\ \ sum \ limit_ {i} D_ {i} * Ds_ {i} + \ sum \ limit_ {j} PP_ { j} * PPp_ {j} \ leq k \\ \ sum \ limit_ {i} D_ {i} * Dd_ {i} \ leq \ sum \ limit_ {j} PP_ {j} * PPl_ {j} \\ D_ { i} = {0, 1}, PP_ {j} = {0, 1} $ inline $
Dies kann beispielsweise durch die Simplex-Methode gelöst werden. Gemäß den Bedingungen der Aufgabe müssen wir jedoch nur das maximale Produktionsvolumen (dh den Wert der Zielfunktion) zurückgeben und nicht angeben, welche Felder und welche Auftragnehmer ausgewählt werden sollen. Zusammen mit den Einschränkungen in der Bedingung kann das Problem durch die dynamische Programmiermethode gelöst werden, indem eine Tabelle dp [Länge] [Geld] erstellt wird, wobei Länge die Länge der Pipeline ist, Geld Geld ist. Nachdem Sie die Tabelle korrekt erstellt haben, reicht es aus, den Maximalwert darin zu finden. Dies ist die Antwort. Die Speicherbeschränkungen der Aufgabe reichen zum Erstellen aus.
Die Aufgabe von "Towers and AI"
| Geben Sie ein | Fazit | Zeitlimit | Speicherlimit |
|---|
| Standardeingabe oder input.txt | Standardausgabe oder output.txt | 1 Sekunde | 64 Megabyte |
Artem entwickelt künstliche Intelligenz für ein wettbewerbsfähiges Handyspiel. Die Spielregeln sind einfach.
Vor den Spielern befinden sich n Türme mit einer Höhe von c 1 ... c i ... c n . In seinem Zug kann der Spieler einen der Türme brechen, so dass mehrere kleinere Türme erhalten werden. Die Spieler haben Angst, in den Türmen verwirrt zu werden, und einigten sich daher auf eine Einschränkung: Nach der Trennung sollten nicht zwei Türme gleicher Höhe erhalten werden. Beispielsweise kann ein Turm mit einer Höhe von 7 in (1, 2, 4) unterteilt werden, nicht jedoch in (1, 3, 3). Die Höhe ist immer eine ganze Zahl.
Verliert den, der keine Türme hat, die zerstört werden können.
Artem hat einen sehr klugen Freund, der optimal spielt - mit ihm kämpft Artems künstliche Intelligenz. Um die Arbeit der KI zu bewerten, muss Artyom wissen, ob der Roboter gewinnen sollte, wenn beide Spieler optimal handeln. Hilf ihm dabei.
Der Mensch geht immer zuerst. Er wird mit AI k Spielen spielen.
Die erste Zeile enthält eine ganze Zahl k <500.
Darauf folgen k Blöcke mit zwei Zeilen.
Die erste Zeile jedes Blocks ist eine ganze Zahl 0 <n ≤ 50.
Die zweite Zeile jedes Blocks hat n ganze Zahlen 0 <c i ≤ 50. Die Zahlen sind durch Leerzeichen getrennt.
k Zeilen, von denen jede wahr oder falsch enthält, je nachdem, ob eine Person das Spiel gewinnt.
Beispiele
| Geben Sie ein | Fazit |
2
1
4
2
1 1 | falsch
falsch |
Parsen
Das vorgeschlagene Turmspiel ist ein gerechtes Endspiel für zwei Spieler, bei dem es unmöglich ist, zu ziehen.
Daher wird der Sieg eines bestimmten Spielers im Spiel durch den Status des Spiels und die Reihenfolge der Züge der beiden Spieler bestimmt. Für Leser, die mit der Spieltheorie vertraut sind, ist es offensichtlich, dass jedes der gleichen Spiele von zwei Spielern tatsächlich dem "er" -Spiel entspricht, was auch unser Spiel bedeutet.
Hier ist eine kurze Beschreibung von ihm - ein Spiel ( Link zur Quelle - klicken Sie darauf für eine detaillierte Überprüfung):
Es gibt mehrere Stapel, von denen jeder mehrere Steine hat. In einem Zug kann der Spieler eine beliebige Anzahl von Steinen ungleich Null von einem Stapel nehmen und wegwerfen. Dementsprechend tritt ein Verlust auf, wenn keine Züge mehr übrig sind, d.h. Alle Stapel sind leer.
Der Zustand des Spiels "er" wird also eindeutig durch eine ungeordnete Menge natürlicher Zahlen beschrieben. In einem Zug darf eine der Zahlen streng reduziert werden (wenn die Zahl dadurch Null wird, wird sie aus dem Satz entfernt).
Die Lösung für das Nim-Spiel besteht darin, die xor-Summe aus der Größe der Haufen zu ermitteln. Nur wenn diese Summe ungleich Null ist, können wir eindeutig feststellen, dass wir uns in einem Gewinnzustand befinden.
Ferner hilft uns das Sprag-Grandi-Theorem, das besagt, dass der Zustand U eines gleichen Spiels von zwei Spielern mit einer Handvoll von ihm-Spielen der Größe X assoziiert werden kann. Sobald eine Funktion, die die Zuordnung der Zustände unseres Spiels zu ihm spezifiziert, ein Spiel ist, wird die Lösung des Problems reduziert um es zu lösen - ein Spiel, das bereits bekannt ist.
Aufgabe „Bewertungsanzeige“
| Geben Sie ein | Fazit | Zeitlimit | Speicherlimit |
|---|
| Standardeingabe oder input.txt | Standardausgabe oder output.txt | 1 Sekunde | 64 Megabyte |
Galya entwickelt einen Bewertungsaggregator. Sie beschloss, die Bewertungen von Institutionen mit Hilfe von siebenzackigen Sternen zu bestimmen.
Das Eingabe-Rendering-System empfängt ein Rechteck mit der Höhe h und der Breite w, dessen obere linke Ecke sich am Punkt (x, y) befindet. Ein Stern muss nach folgenden Regeln gezeichnet werden:
- Die Größe eines Sterns wird durch die Breite oder Höhe des Rechtecks bestimmt - das heißt, kleiner. (Siehe Zeichnungen.)
- Wenn eine der Dimensionen des Rechtecks größer als die entsprechende Dimension des Sterns ist, sollte der Stern auf dieser Dimension zentriert sein.
- Der Stern ist nach oben gerichtet.
Das Rendering-System erwartet die Koordinaten der Eckpunkte des Sterns vom Gali-Code. Hilf Gale, sie zu berechnen.
Um einen siebenzackigen Stern zu bauen, nimmt Galya die äußere Kontur der Figur, die durch Verbinden der Eckpunkte eines regulären Siebenecks durch einen erhalten wird. Im Koordinatensystem ist die X-Achse von links nach rechts und die Y-Achse von oben nach unten gerichtet. Das Gali-Programm stürzt nicht ab und empfängt falsche Werte für Breite und Höhe als Eingabe.
Eine einzelne Zeile enthält Ganzzahlen x, y, w und h, die durch Leerzeichen getrennt sind.
Beispiel: Der Eintrag 150 0 50 100 bezeichnet ein Rechteck mit einer Breite von 50 Punkten, einer Höhe von 100 Punkten und der oberen linken Ecke am Punkt (150, 0).
Die einzige Linie mit 28 durch Leerzeichen getrennten Zahlen sind die Koordinaten der Eckpunkte des Sterns, beginnend von oben und dann im Uhrzeigersinn. Zahlen müssen auf die nächste ganze Zahl gerundet werden. Sehen Sie sich ein Beispiel für die Ausgabe und eine Illustration des Problems an, bevor Sie mit der Lösung fortfahren.
Beispiel: Die Ausgabe von drei Punkten (1, 2), (3, 4), (5, 6) sollte folgendermaßen aussehen: 1 2 3 4 5 6.
Beispiele
| Geben Sie ein | Fazit |
0 0 100 100 | 50 1 65 21 90 21 85 45 100 64 78 75 72 99 50 88 28 99 22 75 0 64 15 45 10 21 35 21 |
Anmerkungen
Die erforderliche Genauigkeit beträgt 10 signifikante Stellen.
Koordinatensystem: X-Achse ist von links nach rechts gerichtet, Y-Achse von oben nach unten:
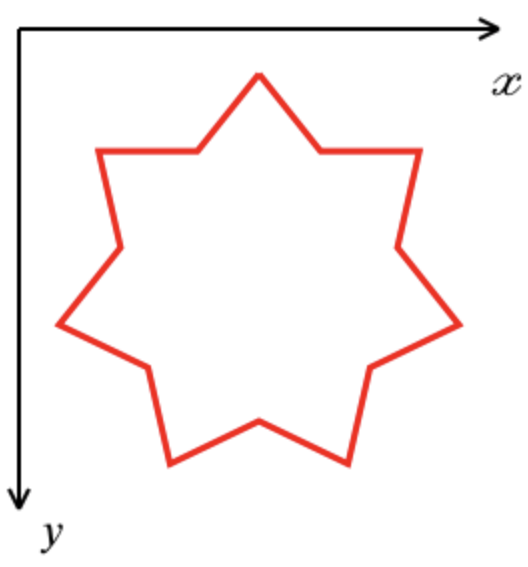
- Erwartete Scheitelpunktreihenfolge:
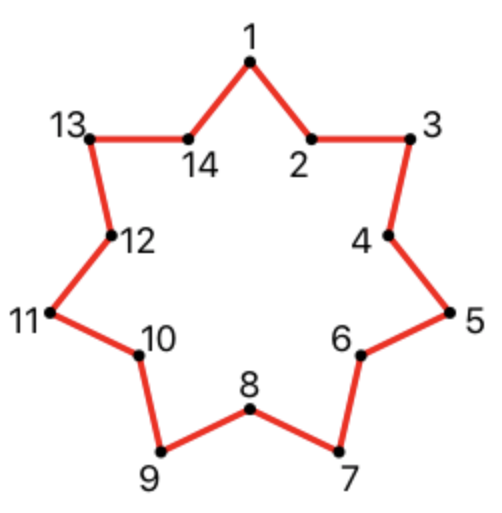
Beispiele für eingeschriebene Sterne:
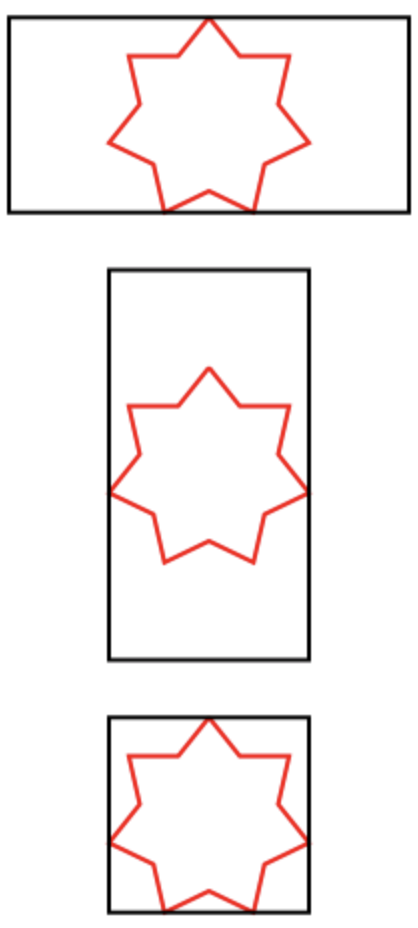
Parsen
Die Lösung des Problems reduziert sich auf drei Stufen: Um einen Referenzstern mit der gewünschten Ausrichtung im Raum zu erstellen, skalieren Sie die resultierenden Punkte, berechnen Sie den Offset und wenden Sie ihn an.
Einen Stern bauen
Am einfachsten ist es, einen Stern zu bauen, der in einen Kreis mit einem am Ursprung zentrierten Einheitsradius eingeschrieben ist. Die Punkte der externen Eckpunkte werden mithilfe der trivialen Trigonometrie berechnet, bei den internen ist die Aufgabe jedoch etwas komplizierter. Sie können auf mindestens zwei Arten gefunden werden. Eine einfachere Möglichkeit besteht darin, die Schnittpunkte der Segmente zu finden, die die äußeren Eckpunkte verbinden. Komplizierter ist es, eine Formel zur Berechnung des Radius eines Beschriftungskreises aus dem Radius eines umschriebenen Kreises zu finden. Der einfachste Weg, dies zu tun, ist beispielsweise für einen 5-Punkt-Stern und verallgemeinert auf den N-Punkt-Stern mit einer beliebigen Lücke zwischen den verbundenen Eckpunkten.
Skalieren
In allen Fällen wird die Größe angegeben, in die der Stern passen muss. Daher müssen wir die erhaltenen Punkte so skalieren, dass der Abstand vom äußersten zum rechten Rand die angegebene Breite nicht überschreitet und der Abstand vom höchsten zum niedrigsten die angegebene Höhe nicht überschreitet. Wir nehmen die Skalierungsfaktoren, um die Breite und Höhe auf die gewünschten Werte zu bringen, und wählen den kleineren aus. Da wir umsichtig einen Referenzstern mit dem Mittelpunkt am Ursprung erstellt haben, reicht es aus, die Koordinaten jedes Punkts einfach mit dem ausgewählten Koeffizienten zu multiplizieren.
Offset
Als letztes müssen wir unsere Punkte so verschieben, dass sich der Stern innerhalb der vorgegebenen Rahmen befindet. Die Eingabedaten aller Optionen können auf einen Begrenzungsrahmen mit einer bestimmten Koordinate der oberen linken Ecke reduziert werden. Hier ist alles einfach: Wir nehmen den höchsten Punkt aus den Ergebnissen der letzten Stufe, betrachten die Differenz seiner y-Koordinate zur y-Koordinate der oberen linken Ecke und verschieben alle Punkte vertikal um den erhaltenen Wert. Wir machen dasselbe mit der x-Koordinate, nehmen nur nicht den obersten Punkt, sondern den ganz linken. Es gibt noch einen letzten Schliff: Zentrieren Sie den Stern in diesem Rechteck.
Weitere Maßnahmen hängen davon ab, welchen Koeffizienten wir in der vorherigen Phase gewählt haben:
- Wenn in der Höhe skaliert, nehmen wir den Unterschied zwischen der Breite des Rechtecks und dem Abstand vom linken zum äußersten rechten Punkt.
- Wenn in der Breite skaliert, nehmen wir die Differenz zwischen der Höhe des Rechtecks und dem Abstand vom höchsten zum niedrigsten Punkt.
Teilen Sie den erhaltenen Wert durch 2 und verschieben Sie die Punkte entsprechend der entsprechenden Messung. Antwort erhalten.
Die Aufgabe „Drehung und Skalierung eines Kreises“
| Geben Sie ein | Fazit | Zeitlimit | Speicherlimit |
|---|
| Standardeingabe oder input.txt | Standardausgabe oder output.txt | 1 Sekunde | 64 Megabyte |
Vika entwickelt einen Grafikeditor für Smartphones und Tablets. Sie möchte dem Benutzer die Möglichkeit geben, einen Kreis auf dem Bildschirm mit zwei Fingern zu drehen und seine Größe wie folgt zu ändern:
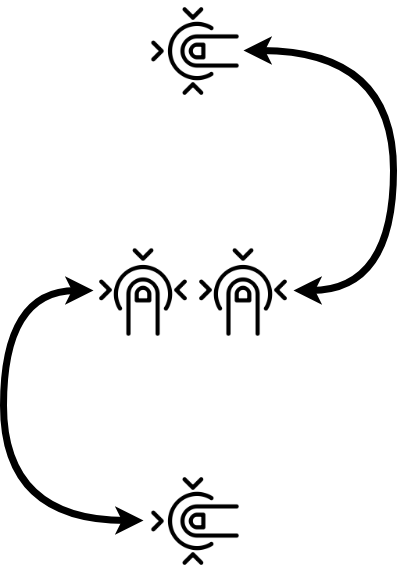
Die Figur dreht sich im gleichen Winkel wie das Segment, das die Finger verbindet. Die Größe der Figur ändert sich proportional zur Länge des Segments. Zuerst wird die Figur gedreht und dann ihre Größe geändert. Anfangs hat der Kreis die Koordinaten (x, y) und den Radius r. Eine Liste von Berührungsereignissen, die die Geste des Benutzers beschreiben, wird angegeben. Hilf Vika, die endgültigen Koordinaten des Kreismittelpunkts und seines Radius zu berechnen. Der Kreis dreht sich relativ zum Punkt (a, b).
Die Beschreibung des Berührungsereignisses enthält die Finger-ID, die Koordinaten und die Art des Ereignisses. Der erste Finger, den der Benutzer angehängt hat, erhält die ID 0, der zweite die ID 1 usw.
Ein Beispiel:
0 337 490 ACTION_DOWN - Dies bedeutet, dass mit dem Finger 0 am Punkt (337, 490) das Ereignis ACTION_DOWN aufgetreten ist.
Es gibt folgende Arten von Berührungsereignissen:
- ACTION_DOWN - Der Benutzer hat an einer bestimmten Stelle den ersten Finger auf den Bildschirm gelegt.
- ACTION_POINTER_DOWN - Der Benutzer hat an einer bestimmten Stelle einen zweiten Finger auf den Bildschirm gelegt.
- ACTION_MOVE - Der Benutzer hat seinen Finger zu einem bestimmten Punkt bewegt.
- ACTION_POINTER_UP - Der Benutzer hat den zweiten Finger an den angegebenen Punkt bewegt und freigegeben.
- ACTION_UP - Der Benutzer hat den ersten Finger an den angegebenen Punkt bewegt und losgelassen.
- ACTION_CANCEL - Benutzer hat die Geste abgebrochen.
Die erste Zeile enthält die durch Leerzeichen getrennten Zahlen x, y und r. Die zweite Zeile enthält die durch Leerzeichen getrennten Zahlen a und b. Die nächsten Zeilen enthalten aufeinanderfolgende Berührungsereignisse.
Die einzige Linie mit Koordinaten und Radius. Zahlen werden durch Leerzeichen getrennt.
Beispiel
| Geben Sie ein | Fazit |
252 194 78
445,559
0 337,490 ACTION_DOWN
1,599,490 ACTION_POINTER_DOWN
1,576,564 ACTION_MOVE
1,552,590 ACTION_MOVE
0 407,375 ACTION_MOVE
1 505 615 ACTION_MOVE
1 482 620 ACTION_MOVE
0 477 360 ACTION_MOVE
1.435.616 ACTION_MOVE
1.411.607 ACTION_MOVE
0 547 386 ACTION_MOVE
1 364 548 ACTION_POINTER_UP
0 571 387 ACTION_UP | 831 704 73 |
Anmerkungen
Bei der Anzeige des Ergebnisses müssen alle Gleitkommawerte gemäß den Regeln der mathematischen Rundung auf einen ganzzahligen Wert gerundet werden.
Parsen
Trotz der Tatsache, dass die Geste kompliziert erscheint, kann sie in zwei Komponenten unterteilt werden: Rotation und Skalierung. Um die Figur zu drehen, müssen wir den Drehwinkel berechnen, der mit der folgenden Formel erhalten werden kann:
a = atan2 (prevTouchX2 - prevTouchX1, prevTouchY2 - prevTouchY1) - atan2 (currentTouchX2 - currentTouchX1, currentTouchY2 - currentTouchY1).
Nachdem Sie den Drehwinkel erhalten haben, müssen Sie die Figur selbst drehen, wodurch sich jeder Punkt der Figur um den Drehwinkel dreht. Nachdem wir die Figur gedreht haben, müssen wir sie skalieren. Das Skalieren einer Figur ist ziemlich trivial. Beim Empfang des Ereignisses ACTION_POINTER_DOWN für den zweiten Finger muss der Abstand zwischen dem ersten und dem zweiten Finger berücksichtigt werden. Anschließend können Sie durch Verfolgen des Abstands zwischen den ersten beiden Fingern den Koeffizienten berechnen, um den Sie die Figur skalieren müssen.
Die Aufgabe "Straßenbau"
| Geben Sie ein | Fazit | Zeitlimit | Speicherlimit |
|---|
| Standardeingabe oder input.txt | Standardausgabe oder output.txt | 1 Sekunde | 64 Megabyte |
In einem Handyspiel baut die Hauptfigur eine Basis auf einem entfernten Planeten auf. Er beginnt mit den Begrenzungstürmen, die durch direkte Laserwände verbunden sind. Architekten vom Hauptquartier schicken ihm einen Plan mit n Türmen mit Koordinaten (x 1 , y 1 ) ... (x i , y i ) ... (x n , y n ). Unter dem Gesichtspunkt der Basisverteidigung ist es nicht sinnvoll, drei oder mehr benachbarte Türme auf einer geraden Linie zu platzieren. Die Personalarchitekten positionieren die Türme jedoch manchmal auf diese Weise, sodass der Spieler selbst die zusätzlichen Zwischentürme entfernen muss.
Nachdem der Held mit dem Perimeter fertig ist, beginnt er, die Basis von innen auszurüsten. Er möchte k Straßen zwischen den Türmen bauen - die Straße kann zwei nicht benachbarte Türme verbinden, aber keine andere Straße oder Mauer überqueren. Aus einem Turm können so viele Straßen kommen, wie Sie möchten.
Der Held hat Straßenroboter. Um den optimalen Straßenbauplan zu wählen, weist der Held sie an, alle möglichen Optionen zu sortieren. Roboter beginnen gleichzeitig und immer wieder zu arbeiten und bieten gleichzeitig einzigartige Möglichkeiten für die Standortbestimmung von Straßen. Wenn sich vor der nächsten Iteration herausstellt, dass weniger Optionen übrig sind als Roboter, werden die zusätzlichen Roboter freigegeben und in die Küche geschickt, um das Abendessen zu kochen. Die verbleibenden Roboter beenden die letzten Optionen und schalten sich aus.
Wenn sich herausstellt, dass Sie die Straße außerhalb der Basis pflastern können, erklärt der Held die Basis für unsicher und fliegt vom Planeten weg.
Wie viele Roboter werden in der Küche arbeiten?
Die erste Zeile enthält drei ganze Zahlen 4 ≤ n ≤ 10 7 , 1 ≤ k ≤ n und eine Primzahl 105 <p <11 × 104. Die Zahlen sind durch Leerzeichen getrennt.
Die nächsten n Zeilen enthalten zwei Ganzzahlen 0 <x i , y i <109. Die Zahlen sind durch Leerzeichen getrennt.
Die einzige Zeile mit der Antwort. Wenn die Basis nicht sicher ist, drucken Sie -1.
Beispiel 1
| Geben Sie ein | Fazit |
4 1 101363
0 0
1 0
1 1
0 1 | 101361 |
Es gibt zwei Möglichkeiten, die einzige Straße zu ebnen: (0, 0) - (1, 1) und (1, 0) - (0, 1). Zwei Roboter werden mit ihnen beschäftigt sein, und der Rest wird in die Küche gehen: p - 2 = 101 361.
Beispiel 2
| Geben Sie ein | Fazit |
4 1 101363
1 0
2 0
0 1
1 2 | -1 |
Hier können Sie eine Straße zwischen (1, 0) - (0, 1) bauen, die sich außerhalb der Basis befindet. Der Held erkennt die Basis als unsicher, die Antwort lautet -1.
Beispiel 3
| Geben Sie ein | Fazit |
4 1 101363
0 0
1 0
2 0
0 1 | 101363 |
Die Türme (0, 0), (1, 0) und (2, 0) befinden sich auf derselben Linie, sodass der Held den mittleren Turm (1, 0) nicht bauen wird. Es kann keine Straße asphaltiert werden, daher gehen alle Roboter sofort in die Küche: p = 101 363.
Parsen
Wir teilen die Lösung des Problems in drei Schritte.
Der erste Schritt besteht darin, für den eingegebenen Scheitelpunktdatensatz zu bestimmen, ob das Polygon konvex ist und wenn ja, wie viele reale Scheitelpunkte es hat. Ein Polygon ist konvex, wenn sich alle seine Eckpunkte auf einer Seite der Linie befinden, die eine Kante trägt. Für jedes Tripel benachbarter Eckpunkte $ inline $ (x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1}) $ inline $ baue ein paar Vektoren $ inline $ ab = ((x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i})) und bc = ((x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1})) $ inline $ und berechnen Sie das Vorzeichen des Ausdrucks ab.x bc.y - bc.x ab.y. Wenn der Ausdruck 0 ist, liegen die Scheitelpunkte auf einer geraden Linie, und je nach Problembedingung verschwindet der im mittleren Scheitelpunkt stehende Turm, wodurch sich die Gesamtzahl der Türme verringert. Wenn für alle Dreiergruppen von Eckpunkten das Produktzeichen 0 oder immer gleich ist, fahren Sie mit dem zweiten Schritt fort. Wenn nicht, betrachten wir die Basis als unsicher und drucken die Antwort -1 aus.
Zweiter Schritt. Die Anzahl der Möglichkeiten, k disjunkte Diagonalen innerhalb eines konvexen N-Gons zu konstruieren, beträgt $ inline $ V = 1 / (k + 1) {N-3 \ wähle k} {N + k-1 \ wähle k} $ inline $ , aber wir müssen den Ausdruck p - V mod p berechnen, wobei p eine Primzahl ist.
Stellen Sie sich N vor! wie $ inline $ a * p ^ e $ inline $ wobei der größte gemeinsame Faktor a ist und p gcd (a, p) = 1 ist.
$ inline $ {n \ wähle r} = (n!) / (r! (nr)!) = a_ {1} * p ^ {e_ {1}} / a_ {2} * p ^ {e_ {2} } * a_ {3} * p ^ {e_ {3}} = (a_ {1} / a_ {2} * a_ {3}) * p ^ {e_ {1} -e_ {2} -e_ {3} } $ inline $
Wenn $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ , dann ist der Ausdruck durch p teilbar und die Antwort im Problem ist p.
Für den Fall $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ = 0 die Antwort wird sein $ inline $ a_ {1} / a_ {2} * a_ {3} $ inline $ mod p.
Bei der Berechnung berücksichtigen wir, dass a b mod p = (a mod p) (b mod p) mod p und $ inline $ k ^ {- 1} $ inline $ mod p = $ inline $ (k) ^ {p-2} $ inline $ mod p für prime p.
Dritter Schritt. Den Ausdruck berechnen $ inline $ e_ {1} -e_ {2} -e_ {3} $ inline $ stell dir n vor! als 1 2 ... p (p + 1) ... 2p (2p + 1) ..., während (p + 1) ... (2p-1) mod p = 1 2 ... (p-1 ) = (p-1)! .. Insgesamt n mod p = ( $ inline $ (p-1)! ^ k $ inline $ k (n mod p)!) mod p, wobei k = Boden (n / p).
Aufgabe “Super Simple Scheduler”
| Geben Sie ein | Fazit | Zeitlimit | Speicherlimit |
|---|
| Standardeingabe oder input.txt | Standardausgabe oder output.txt | 10 Sekunden | 224 Megabyte |
Auf dem Smartphone-Prozessor müssen n Aufgaben ausgeführt werden. Ihre Implementierung erfordert t 1 ... t i ... t n Zeiteinheiten, und zu Beginn der d-ten Zeiteinheit muss die i-te Aufgabe abgeschlossen sein.
Um rechtzeitig zu sein, können Aufgaben in mehreren Threads ausgeführt werden. Jeder neue Thread führt jedoch zu einer zunehmenden Belastung der Batterie. Im ersten Strom wird eine Energieeinheit pro Zeiteinheit verbraucht, in den zweiten eineinhalb Energieeinheiten, in den dritten eineinhalb Mal mehr als in der zweiten usw.
Aufgaben können in Zeiteinheiten unterteilt werden: zuerst eine teilweise abschließen, dann zu einer anderen übergehen und dann zur ersten zurückkehren. Sie können nicht gleichzeitig verschiedene Teile einer Aufgabe in verschiedenen Threads ausführen.
Der Scheduler empfängt Aufgaben einzeln. Nachdem er eine Aufgabe erhalten hat, weist er ihr sofort Zeitfenster zu. Nachdem die Aufgabe verteilt wurde, kann der Scheduler sie nicht mehr auf andere Slots übertragen.
Wie viel Energie wird benötigt, um alle Aufgaben zu erledigen, wenn sie optimal verteilt sind?
Die erste Zeile enthält die ganze Zahl 1 <n ≤ 3 × 10 3 .
Die nächsten n Zeilen enthalten zwei ganze Zahlen 0 ≤ t i ≤ 10 4 und 0 ≤ d i ≤ 10 4 . Zahlen werden durch Leerzeichen getrennt.
Die einzige Zeile mit der Antwort. Genauigkeit - acht Dezimalstellen.
Beispiel
| Geben Sie ein | Fazit |
5
2 2
1 1
3 4
1 10
1 2 | 10.25000000 |
Parsen
Da es gemäß den Bedingungen des Problems ausreicht, nur die verbrauchte Energiemenge zu berechnen, können wir die Lösungsmethode verwenden, indem wir die verbrauchte Energiemenge für jede Zeiteinheit berechnen. Bei der Planung der Aufgabe nehmen wir den Mindestwert der verbrauchten Energie k = 1 und sortieren ab dem Stichtag der Aufgabe alle Slots des Zeitintervalls.
Wenn der Energieverbrauch des Schlitzes kleiner als der Koeffizient (k) ist und dieser Zeitschlitz bei der Planung der Aufgabe nicht verwendet wurde, belegen wir diesen Schlitz, um die Aufgabe abzuschließen, indem wir den Koeffizienten des Schlitzes um K erhöhen. Wenn wir den Beginn des Zeitraums erreichen, müssen wir den Koeffizienten k um das 1,5-fache und erhöhen Wiederholen Sie die Suche nach Zeitfenstern ab dem Stichtag und bis die Aufgabe vollständig geplant ist. Nach Abschluss der Planung aller Aufgaben muss nur noch der Gesamtenergieverbrauch durch Addition der Koeffizienten jeder Zeiteinheit berechnet werden.
Die Aufgabe "Zerstörbare Objekte"
| Geben Sie ein | Fazit | Zeitlimit | Speicherlimit |
|---|
| Standardeingabe oder input.txt | Standardausgabe oder output.txt | 2 Sekunden | 64 Megabyte |
2D- . , : n- (x 1 , y 1 )...(x i , y i )...(x n , y n ). — , . . , — , .
, [0 1 2 3 4], 1 3 1 3, [1 2 3] [0 1 3 4].
, . . , , .
, ?
n ≤ 500. n x y. .
. — .
Beispiel 1
| Fazit |
4
100 100
200 100
200 200
100 200 | 0.000000 |
2
| Fazit |
6
167 84
421 84
283 192
433 298
164 275
320 133 | 326.986753 |
, , . « » : — . : , ( ) .
, ? ( , , ). : , , , . , , ( ) . even-odd rule: . — , ( ) , — .
, , — , . (, , ):
- ( );
- : , - ;
- ( , 10-5 );
- even-odd rule — ;
- : 180 .
«DNA»
| Fazit | | |
|---|
| input.txt | output.txt | 8 | 128 |
, . , , . n . , . : A, T, G C. . .
n. n . . 6⋅10 6 .
. . . . . , .
Beispiel
( , ):
5
TTT
GAAGCT
CAAT
AGA
AGGCA
:
2 TTT
6 AGA
28 AGA
30 AGA
57 CAAT
86 AGA
100 GAAGCT
190 TTT
191 TTT
196 AGA
219 TTT
232 AGA
271 TTT
284 TTT
285 TTT
298 TTT
320 TTT
330 TTT
331 TTT
342 TTT
373 AGA
397 AGA
488 AGA
509 AGA
524 AGA
565 TTT
574 AGA
605 AGA
625 CAAT
630 AGA
681 CAAT
718 TTT
719 TTT
744 AGGCA
754 AGA
784 AGA
808 TTT
821 CAAT
833 AGA
861 CAAT
879 AGA
921 AGA
955 AGA
, . — , — . , . . , .
, .
«QR Quest»
| Fazit | | |
|---|
| input.txt | output.txt | 1 | 64 |

t, . t n i , .
t , .
Beispiel 1
| Fazit |
4
8 10 1 9 2 6 7 8
14 2 0 11 10 4 1 0
6 6 4 1 10 0 11 6
11 4 3 4 14 8 12 5 | 0
13
15
5 |
2
| Fazit |
4
9 10 6 2 12 11 7 2
3 10 1 14 13 13 1 1
6 8 8 5 3 2 6 4
5 11 5 5 3 1 10 7 | 3
9
2
7 |
, . QR- , . - .
Insgesamt wurden acht Zahlen eingegeben - die Koordinaten der Zellen in diesen Tabellen, dh 4 Paare mit den Koordinaten der Spalte und Zeile. Es musste erraten werden, welche Operation mit diesen Zellen durchgeführt wurde und aus welcher Tabelle eine zusätzliche Zelle stammte.
Mit einfachen Manipulationen könnte man überprüfen, ob dies die xor-Summe für vier Zellen der Tabellen A, B und C ist, die durch die Indizes a 0 ... a 7 adressiert sind :
R = A [a 0 , a 1 ] ^ B [a 2 , a 3 ] ^ B [a 4 , a 5 ] ^ C [a 6 , a 7 ].