Beweis von Orten, an denen keine Symmetrien existieren können

Eine wichtige mathematische Errungenschaft war die Zimmer-Hypothese, die von einem kleinen Forscherteam gefunden wurde.

Bei Gittern mit höheren Symmetriedimensionen ist es nicht immer möglich, auf Dimensionen unterhalb des Ranges zu übertragen

Der Erfolg von Robert Zimmer kann auf viele Arten definiert werden. Als Präsident der University of Chicago seit 2006 machte er Schlagzeilen und fand neunstellige Beträge für die Finanzierung und Veröffentlichung von Artikeln zur Unterstützung der Meinungsfreiheit auf dem Campus. Bevor er Präsident der Universität wurde, war er Mathematiker. Und lange nachdem er ernsthafte Forschungen verlassen hatte, liefert der von ihm gestartete Forschungsplan endlich seine Ergebnisse.

Vor einem Jahr haben drei Mathematiker die Hypothese von Zimmer in Bezug auf Umstände bewiesen , unter denen geometrische Räume Symmetrien eines bestimmten Typs aufweisen. Ihr Beweis ist zu einer der größten mathematischen Errungenschaften der letzten Jahre geworden. Damit ist die Frage beendet, die sich Zimmer während seiner intensiven mentalen Aktivität Ende der 1970er und Anfang der 1980er Jahre stellte.

"Ich würde sagen, dass ich jeden Abend fünf Jahre lang mit Gedanken über diese Aufgabe ins Bett gegangen bin, also war ich davon besessen, und es ist großartig zu sehen, wie die Leute es gelöst haben", sagte Zimmer.

Je größer der geometrische Dimensionsraum ist, desto mehr Symmetrien können normalerweise darin enthalten sein. Dies kann man sich vorstellen, indem man einen Kreis untersucht, der auf einer zweidimensionalen Ebene existiert, und eine Kugel, die sich in drei Dimensionen erstreckt: Es gibt mehr Möglichkeiten, die Kugel zu drehen, als es Möglichkeiten gibt, einen Kreis zu drehen. Zusätzliche Kugelabmessungen erzeugen zusätzliche Symmetrien.

Die Vermutung von Zimmer bezieht sich auf Symmetrien einer besonderen Art, die als hochrangige Gitter bekannt sind. Sie fragt, ob die Messung des geometrischen Raums die Verwendung derartiger Symmetrien einschränkt. Die Autoren der neuen Arbeit - Aaron Brown und Sebastian Hurtado-Salazar von der University of Chicago und David Fisher von der Indiana University - zeigten, dass bei der Anzahl der Messungen weniger als eine bestimmte spezifische Symmetrie nicht beobachtet wird. Damit haben sie die Richtigkeit von Zimmer's Hypothese bewiesen.


Robert Zimmer, heute Präsident der University of Chicago, entwickelte vor fast 40 Jahren eine nach ihm benannte Hypothese

Ihre Arbeit beantwortet eine wichtige und lang anhaltende Frage und eröffnet neue Möglichkeiten, viele andere zu studieren. Es zeigt auch die intrinsischen Eigenschaften geometrischer Räume. Symmetrie ist eine der einfachsten Eigenschaften solcher Räume. Die neue Arbeit besagt, dass Symmetrien in Räumen eines Typs existieren können und nicht in anderen. Dieser Erfolg wurde nach Jahrzehnten der Ausfallzeit erreicht.

"Die Hypothese sah so aus, als könnte sie die Menschen sehr lange beschäftigen", sagte Amy Wilkinson, Mathematikerin an der Universität von Chicago, die die diesjährige Konferenz zu diesem Beweis organisierte. "Und sie haben diese Frage relativ einfach zerstört."

Symmetrien befriedigen

Symmetrie ist eines der ersten geometrischen Konzepte, auf die Kinder in der Mathematik stoßen. Mit ihren eigenen Händen lernen sie, dass Sie das Formular drehen, drehen und verschieben können und am Ende das gleiche Formular erhalten, mit dem sie begonnen haben. Das Erhalten der Form des Objekts als Ergebnis von Änderungen reagiert mit einer gewissen inneren Befriedigung - dies ist ein Hinweis auf eine tiefere Ordnung im Universum.

Mathematiker haben ihre eigene formale Sprache für das Studium der Symmetrie. Es gibt ihnen die Möglichkeit, verschiedene Symmetrien, die in einem bestimmten geometrischen Raum anwendbar sind, kurz zu diskutieren.

Ein Quadrat hat zum Beispiel acht Symmetrien - acht Möglichkeiten, es umzudrehen oder zu drehen, um das Quadrat wieder zu erhalten. Der Kreis kann um eine beliebige Anzahl von Grad gedreht werden. Sie hat unendlich viele Symmetrien. Mathematiker sammeln alle Symmetrien eines bestimmten geometrischen Objekts oder Raums und packen sie in eine „Gruppe“.

Gruppen sind an sich interessant. Sie erscheinen oft als Ergebnis der Untersuchung bestimmter geometrischer Räume, aber manchmal erscheinen sie in einem Kontext, der völlig unabhängig von der Geometrie ist. Zum Beispiel können Gruppen numerische Mengen bilden (zum Beispiel gibt es eine gewisse Symmetrie beim Addieren von 5 oder Subtrahieren von 5 von einer Zahl).

"Eine Gruppe kann im Prinzip als Symmetrie völlig unterschiedlicher Dinge erscheinen", sagte Zimmer.

Es gibt exotischere Formen der Symmetrie als die, die wir in der Schule lernen. Betrachten Sie zum Beispiel die Symmetrie von Gittern. Das einfachste Gitter ist ein zweidimensionales Gitter. In der Ebene kann das Gitter um eine beliebige Anzahl von Quadraten nach oben, unten, links und rechts verschoben werden, um ein Gitter zu erhalten, das genau so aussieht wie das Original. Sie können das Raster auch durch eine beliebige Anzahl einzelner Zellen reflektieren. Räume mit Gittern haben unendlich viele verschiedene Symmetrien von Gittern.



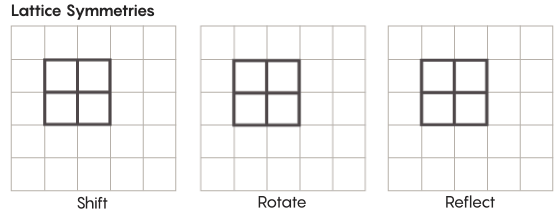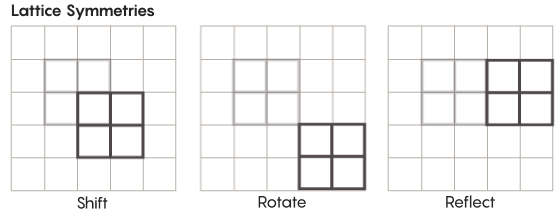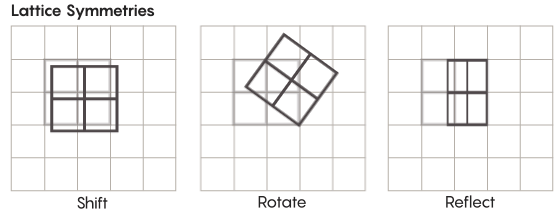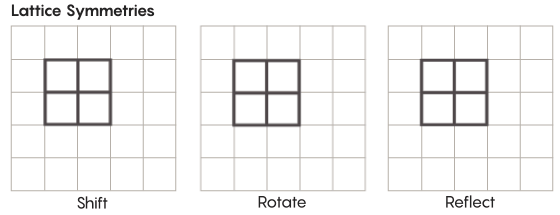
Gitter können in beliebig vielen Dimensionen existieren. Im dreidimensionalen Raum kann ein Gitter aus Würfeln und nicht aus Quadraten bestehen. In vier oder mehr Dimensionen ist es nicht möglich, das Gitter darzustellen, aber es funktioniert auf die gleiche Weise. Mathematiker können es genau beschreiben. Zu den für die Zimmer-Hypothese interessanten Gruppen gehören Gitter mit höherem Rang oder Gitter in bestimmten Räumen mit höheren Dimensionen. "Dieses seltsame Gitter wäre sehr schön, wenn es gesehen werden könnte, selbst wenn es mir nicht gegeben würde", sagte Khurtado-Salazar. "Es scheint mir, dass es sehr schön wäre, sie anzusehen."

Im 20. Jahrhundert entdeckten Mathematiker diese Gruppen unter verschiedenen Bedingungen - nicht nur in der Geometrie, sondern auch in der Zahlentheorie, Logik und Informatik. Wenn Sie neue Gruppen eröffnen, ist es logisch, die Frage zu stellen: Welche Art von Räumen besitzen solche Symmetriesätze?

Manchmal ist es offensichtlich unmöglich, Gruppen mit dem Raum abzustimmen. Man kann ziemlich schnell verstehen, dass die Symmetriegruppe eines Kreises nicht auf ein Quadrat angewendet werden kann. Drehen Sie das Quadrat um 10 Grad und Sie erhalten nicht das ursprüngliche Quadrat. Eine Mischung aus einer Gruppe mit einer unendlichen Anzahl von Symmetrien und einem Raum mit vielen Dimensionen macht es jedoch schwierig, die Anwendbarkeit der Gruppe zu bestimmen.

"Wenn Sie zu einer komplexeren Gruppe in mehr Dimensionen wechseln", sagte Zimmer, "werden diese Probleme sehr kompliziert."

Indirekte Verbindung

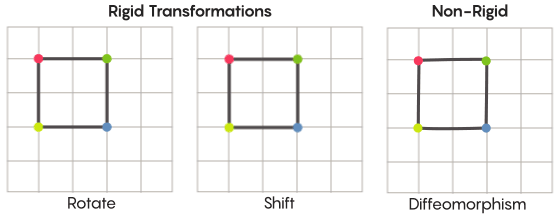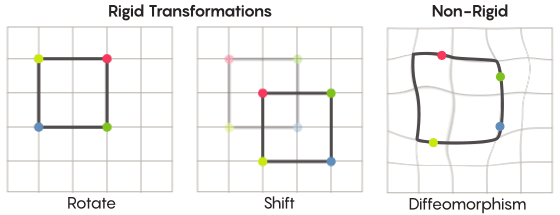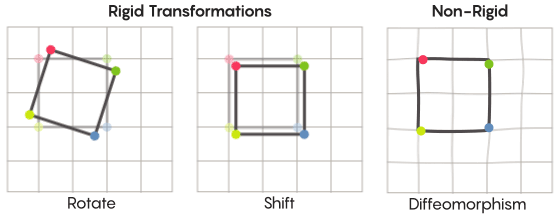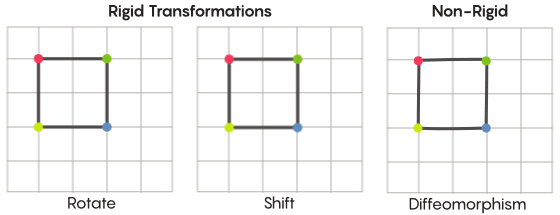
Wenn wir uns Symmetrie vorstellen, stellen wir uns die Drehung der gesamten Form vor - zum Beispiel ein um 90 Grad gedrehtes Quadrat. Grundsätzlich hängt die Symmetrie jedoch von sich bewegenden Punkten ab. Symmetrische Transformation des Raums bedeutet, dass Sie jeden Punkt davon nehmen und an einen anderen Punkt verschieben müssen. In diesem Sinne bedeutet eine 90-Grad-Drehung des Quadrats tatsächlich, dass Sie jeden Punkt des Quadrats nehmen und um 90 Grad drehen müssen, damit er sich nicht an der Kante befindet, von der aus Sie begonnen haben.


David Fischer

Das Problem der Bewegungspunkte kann mehr oder weniger streng gelöst werden. Die bekanntesten symmetrischen Transformationen - die Reflexion eines Quadrats relativ zur Diagonale oder seine Drehung um 90 Grad - sind sehr streng. Streng in dem Sinne, dass sie keine Punkte verwechseln. Die Punkte, die vor der Reflexion Scheitelpunkte waren, bleiben nachher Scheitelpunkte (sie werden nur zu unterschiedlichen Scheitelpunkten), und die Punkte, aus denen die geraden Kanten bestehen, bilden nach der Reflexion immer noch die geraden Kanten (nur unterschiedlich).

Es gibt weniger strenge, flexiblere Arten symmetrischer Transformationen, die im Kontext der Zimmer-Hypothese interessant sind. Bei solchen Transformationen ändern Punkte ihre Organisation stärker. Sie behalten nach der Transformation nicht unbedingt ihre früheren Verbindungen untereinander bei. Sie können beispielsweise jeden Punkt des Quadrats um drei Längeneinheiten entlang des Umfangs des Quadrats verschieben. Dies erfüllt die grundlegenden Anforderungen einer symmetrischen Transformation, dh Sie verschieben einfach jeden Punkt im Raum an einen anderen Ort. Aaron Brown, Mitautor des Beweises, beschrieb, wie diese mehr Freiformtransformationen im Kontext des Balls aussehen könnten.

„Man kann den Nord- und Südpol nehmen und sie in entgegengesetzte Richtungen drehen. Dann wird der Abstand zwischen den Punkten größer “, sagte Brown.

Im Fall eines Gitters können Sie es nicht einfach entlang der Ebene bewegen, sondern biegen, an einigen Stellen dehnen und an anderen Stellen zusammendrücken, sodass das transformierte Netz das ursprüngliche nicht mehr überlappt. Solche Transformationen sind weniger streng und werden Diffeomorphismen genannt .



Zimmer hatte guten Grund, diese weniger strenge Version der Symmetrie in seiner Hypothese zu verwenden. Spezielle Gitter von höchstem Rang im Zusammenhang mit dieser Hypothese wurden erstmals in den 1960er Jahren von Grigory Alexandrovich Margulis untersucht , der für seine Arbeit den Fields-Preis erhielt. Margulis hat vollständig beschrieben, welche Art von Räumen mit diesen höherrangigen Gittern transformiert werden können, wenn nur strenge Transformationen zulässig sind.

Die Hypothese von Zimmer wurde zu einer natürlichen Fortsetzung von Margulis 'Arbeit. Es beginnt mit einer Liste von Räumen, auf denen hochrangige Gitter arbeiten können - Margulis hat diese Liste entdeckt - und fragt, ob diese Liste erweitert wird, wenn die Gitter weniger strenge Transformationen aufweisen dürfen.

In der neuen Arbeit haben drei Mathematiker bewiesen, dass eine Schwächung der Definition von Symmetrie den Umfang der Symmetrien von Gittern höherer Ordnung nicht verändert. Selbst wenn die Gitter sehr unregelmäßige Transformationen aufweisen dürfen - verschieben, biegen, dehnen -, unterliegen die Gitter immer noch einer strengen Einschränkung des Umfangs.

„Nachdem wir der Problemstellung eine solche Flexibilität hinzugefügt haben, scheint es natürlich intuitiv, dass die Gitter breiter wirken können. Daher stellt sich heraus, dass die Antwort in Wirklichkeit "Nein" lautet - in einigen Fällen können sie dies nicht ", sagte Fisher.

Mathematiker haben genaue Entsprechungen zwischen der Dimension des Raums und der Dimension oder dem Rang von Gittern für Gitter hergestellt, die in einem bestimmten Raum die Rolle der Symmetrie spielen können. Im Allgemeinen zeigten sie, dass je höher der Rang des Gitters ist, desto mehr Messungen für den Raum erforderlich sind, der es aufnehmen kann. Selbst bei beträchtlicher Flexibilität bei der Transformation von Räumen sind Transformationen von hochrangigen Gittern auf höhere Dimensionen beschränkt.

"Dies deutet darauf hin, dass die Struktur von Räumen etwas sehr Grundlegendes enthält, was ihre Fähigkeit impliziert, solche Transformationen zu berücksichtigen", sagte Wilkinson.

Die Hypothese von Zimmer ist nur der erste Schritt zu einem größeren Programm. Nachdem sie sich damit befasst hatten, schränkten die Mitautoren der Arbeit die Räume, in denen hochrangige Gitter transformiert werden können, grob ein. Die nächste, ehrgeizigere Phase der Arbeit wird die Konzentration auf die Räume sein, in denen Gitter existieren können - und dann die Klassifizierung aller verschiedenen Arten der Transformation von Gittern dieser Räume.

„Am Ende sollte das Programm in der Lage sein, alle diese Methoden zu klassifizieren. Es gibt viele interessante Fragen, die über die einfache Feststellung der Existenz bestimmter Orte hinausgehen, an denen die Gitter nicht funktionieren können “, sagte Zimmer.