🤚🏻 🏇🏿 🧛🏼 Julia und Phasenporträts dynamischer Systeme 🤷🏻 👨🏼‍⚕️ 🎃

Wir beherrschen weiterhin die junge und vielversprechende Allzwecksprache Julia . Für den Anfang brauchen wir jedoch genau die sehr enge Anwendungsmöglichkeit - zur Lösung typischer Probleme der Physik. Dies ist die bequemste Taktik, um das Instrument zu beherrschen: Um Hand anzulegen, werden wir drängende Probleme lösen, die Komplexität schrittweise erhöhen und Wege finden, um unser Leben leichter zu machen. Kurz gesagt, wir werden Diffusionen lösen und Diagramme erstellen.

Laden Sie zunächst das Gadfly -Grafikpaket und sofort die Vollversion des Entwicklers herunter, damit es mit unserer Julia 1.0.1 gut funktioniert. Wir fahren in unserem REPL-, JUNO- oder Jupyter-Notebook:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master"

Nicht die bequemste Option, aber jetzt warten wir darauf, dass das PlotlyJS- Update versucht, einen Vergleich anzustellen .

Sie benötigen außerdem ein leistungsstarkes Tool zum Lösen von Differentialgleichungen. DifferentialEquations

 ]add DifferentialEquations #

Dies ist das umfangreichste und am meisten unterstützte Paket, das viele Methoden zum Lösen von Unterschieden bietet. Fahren Sie nun mit den Phasenporträts fort.

Lösungen gewöhnlicher Differentialgleichungen sind oft bequemer in ungewöhnlicher Form darzustellen $y ^ 1 (t), ..., y ^ L (t)$ und in dem Phasenraum, entlang dessen Achsen die Werte jeder der gefundenen Funktionen aufgetragen sind. Darüber hinaus ist das Argument t nur parametrisch in den Diagrammen enthalten. Bei zwei ODEs ist ein solcher Graph - das Phasenporträt des Systems - eine Kurve in der Phasenebene und daher besonders deutlich.

Oszillator

Harmonische Oszillatordynamik $\ gamma$ wird durch das folgende Gleichungssystem beschrieben:

d o t x = y d o t y = - o m e g a^{2} x + g a m m a y

$\ dot {x} = y \\ \ dot {y} = - \ omega ^ 2x + \ gamma y$

und unabhängig von den Anfangsbedingungen (x0, y0) kommt es zu einem Gleichgewichtszustand, einem Punkt (0,0) mit einem Ablenkwinkel von Null und einer Geschwindigkeit von Null.

Bei $\ gamma = 0$ Die Lösung hat die für einen klassischen Oszillator charakteristische Form.

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end

Lassen Sie uns den Code analysieren. Die Funktion akzeptiert die Werte des Frequenz- und Dämpfungsparameters sowie die Anfangsbedingungen. Die verschachtelte Funktion syst () definiert das System. Damit sich herausstellte, verwendeten sie eine einzeilige Matrixmultiplikation. Die Funktion remove () , die eine große Anzahl von Parametern verwendet, ist sehr flexibel konfiguriert, um das Problem zu lösen. Wir haben jedoch nur die Lösungsmethode angegeben - Runge-Kutta 4 ( es gibt viele andere ), den relativen Fehler und die Tatsache, dass nicht alle Punkte gespeichert werden sollten, sondern nur jeder vierte . Die Antwortmatrix ist in der Variablen sol gespeichert, außerdem enthält sol.t einen Zeitvektor und sol.u löst das System zu diesen Zeiten. All dies wird ruhig in Plots gezeichnet, und für Gadfly müssen Sie die Antwort in einer bequemeren Matrix vervollständigen. Wir brauchen keine Zeiten, also geben wir nur Lösungen zurück.

Lassen Sie uns ein Phasenporträt erstellen:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2])

Unter den Funktionen broadcast(f, [1, 2, 3]) Ordnung ist broadcast(f, [1, 2, 3]) für uns besonders bemerkenswert, bei dem die Werte des Arrays [1, 2, 3] abwechselnd in die Funktion f eingesetzt werden . Kurze Aufzeichnung f.([1, 2, 3]) . Dies ist nützlich, um die Frequenz, den Dämpfungsparameter, die Anfangskoordinate und die Anfangsgeschwindigkeit zu variieren.

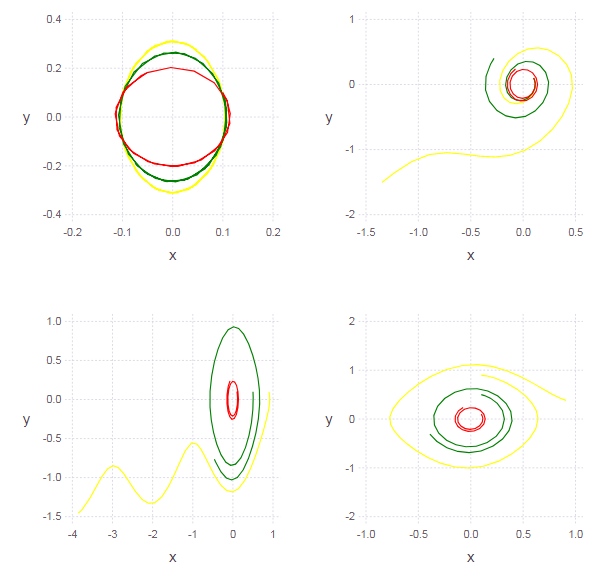
Versteckt unter dem Spoiler

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #

Wir betrachten nun nicht kleine Schwingungen, sondern Schwingungen beliebiger Amplitude:

d o t x = y d o t y = - s i n (o m e g a x) + g a m m a y

$\ dot {x} = y \\ \ dot {y} = - sin (\ omega x) + \ gamma y$

Das Phasendiagramm der Lösung ist keine Ellipse (die die Nichtlinearität des Oszillators anzeigt). Je weniger wir die Amplitude der Schwingungen (d. H. Die Anfangsbedingungen) wählen, desto weniger Nichtlinearität tritt auf (daher können kleine Schwingungen des Pendels als harmonisch angesehen werden).

Versteckt unter dem Spoiler

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) )

Brüsseler

Dieses Modell beschreibt eine bestimmte autokatalytische chemische Reaktion, bei der die Diffusion eine Rolle spielt. Das Modell wurde 1968 von Lefebvre und Prigozhin vorgeschlagen.

d o t u_{1} = - (m u + 1) u_{1} + u_{1}^{2} u_{2} + 1 d o t u_{2} = m u u_{1} - u_{1}^{2} u_{2}

$\ dot {u} _1 = - (\ mu + 1) u_1 + u ^ 2_1u_2 + 1 \\ \ dot {u} _2 = \ mu u_1-u ^ 2_1u_2$

Unbekannte Funktionen $u_1 (t), \, u_2 (t)$ spiegeln die Dynamik der Konzentration von Zwischenprodukten einer chemischen Reaktion wider. Modellparameter $\ mu$ Die Anfangskonzentration des Katalysators (dritte Substanz) ist sinnvoll.

Genauer gesagt kann die Entwicklung des Phasenporträts des Brüsselers beobachtet werden, indem Berechnungen mit verschiedenen Parametern durchgeführt werden $\ mu$ . Mit seiner Zunahme verschiebt sich der Knoten zunächst allmählich zu einem Punkt mit Koordinaten (1, $\ mu$ ) bis es einen Bifurkationswert erreicht $\ mu$ = 2. Zu diesem Zeitpunkt erfolgt eine qualitative Umstrukturierung des Porträts, die sich in der Entstehung des Grenzzyklus äußert. Mit weiterem Anstieg $\ mu$ es tritt nur eine quantitative Änderung der Parameter dieses Zyklus auf.

Versteckt unter dem Spoiler

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) )

Genug für heute. Das nächste Mal werden wir versuchen zu lernen, wie man ein anderes Grafikpaket für neue Aufgaben verwendet, während wir gleichzeitig Julias Syntax eingeben. Bei der Lösung von Problemen, die langsam aufgespürt werden, nicht dass die Vor- und Nachteile einfach sind ... vielmehr Annehmlichkeiten und Unannehmlichkeiten - ein separates Gespräch sollte diesem Thema gewidmet werden. Und natürlich würde ich gerne etwas Ernsthafteres in meinem Habra sehen als meine Spiele mit Funktionen. Deshalb fordere ich die Julisten auf, mehr über ernstere Projekte zu erzählen. Dies würde vielen und insbesondere beim Erlernen dieser wunderbaren Sprache helfen.

Julia und Phasenporträts dynamischer Systeme

Oszillator

Brüsseler

More articles: