⛹🏿 🐔 ➕ Julia und partielle Differentialgleichungen 💇🏼 👨🏻‍💻 🙆🏾

Am Beispiel typischer physikalischer Modelle werden wir die Fähigkeiten der Arbeit mit Funktionen festigen und uns mit dem schnellen, praktischen und schönen PyPlot-Visualizer vertraut machen, der die gesamte Leistung des Matplotlib Python bietet. Es wird viele Bilder geben (versteckt unter den Spoilern)

Wir sorgen dafür, dass unter der Haube alles sauber und frisch ist:

Unter der Haube

]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Ansonsten bekommen wir alles, was wir heute brauchen

 julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot #     build #    -      ,    pkg> add Conda #    Jupyter -    pkg> add IJulia #      pkg> build IJulia #     build

Nun zu den Aufgaben!

Trage Gleichung

In der Physik bedeutet der Begriff Übertragung irreversible Prozesse, aufgrund derer eine räumliche Bewegung (Übertragung) von Masse, Impuls, Energie, Ladung oder einer anderen physikalischen Größe im physikalischen System auftritt.
Die lineare eindimensionale Transportgleichung (oder die Advektionsgleichung) - die einfachste partielle Differentialgleichung - wird wie folgt geschrieben

f r a c p a r t i e l l e s U (x, t) p a r t i e l l e s t + c f r a c p a r t i e l l e s U (x, t) p a r t i e l l e s x = P h i (U, x, t)

$\ frac {\ partielles U (x, t)} {\ partielles t} + c \ frac {\ partielles U (x, t)} {\ partielles x} = \ Phi (U, x, t)$

Für die numerische Lösung der Transportgleichung können Sie das explizite Differenzschema verwenden:

f r a c h a t U_{i} - U_{i} t a u + c f r a c U_{i} - U_{i - 1} D e l t a = f r a c P h i_{i - 1} + P h i_{i} 2

$\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ Phi_ {i-1} + \ Phi_i} {2}$

wo $\ hat {U}$ - Der Wert der Gitterfunktion auf der oberen Zeitschicht. Diese Schaltung ist mit der Courant-Nummer stabil. $K = c \ tau / \ Delta <1$

Nichtlineare Übertragung

f r a c p a r t i e l l e s U (x, t) p a r t i e l l e s t + (C_{0} + U C_{1}) f r a c p a r t i e l l e s U (x, t) p a r t i e l l e s x = P h i (U, x, t)

$\ frac {\ partielles U (x, t)} {\ partielles t} + (C_0 + UC_1) \ frac {\ partielles U (x, t)} {\ partielles x} = \ Phi (U, x, t )$

Linienquelle (Absorptionstransfer): $\ Phi (U, x, t) = - BU$ . Wir verwenden das explizite Differenzschema:

U_{i}^{j + 1} = l e f t (1 - f r a c h_{t} B 2 - f r a c h_{t} C_{0} h_{x} - f r a c h_{t} C_{1} h_{x} U_{i}^{j} r i g h t) U_{i}^{j} + U_{i - 1}^{j} l e f t (f r a c h_{t} C_{0} h_{x} - f r a c h_{t} B 2 + f r a c h_{t} C_{1} h_{x} U_{i}^{j} r i g h t)

$U ^ {j + 1} _i = \ left (1- \ frac {h_tB} {2} - \ frac {h_tC_0} {h_x} - \ frac {h_tC_1} {h_x} U ^ j_i \ right) U ^ j_i + U ^ j_ {i-1} \ left (\ frac {h_tC_0} {h_x} - \ frac {h_tB} {2} + \ frac {h_tC_1} {h_x} U ^ j_i \ right)$

 using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) #   bord = t -> 0. #  #    - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]#         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #

Ergebnis

Erhöhen wir die Absorption:

 t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )

Ergebnis

 t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])

Fast umgekippt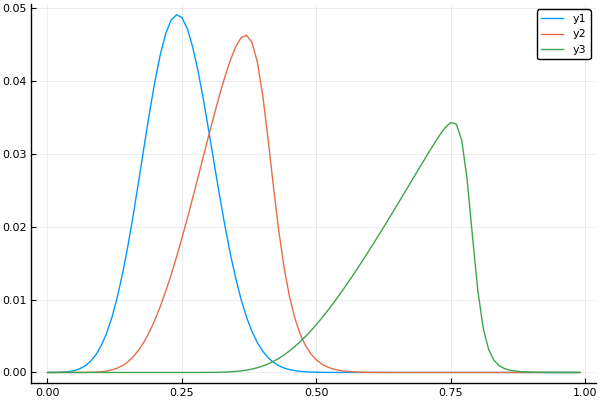

heatmap(t, X, Ans0)

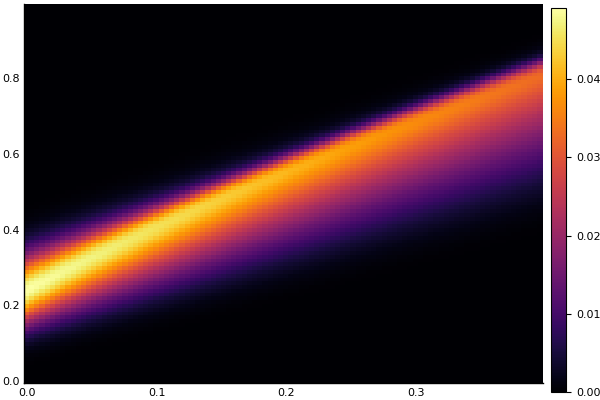
Wärmegleichung

Die Differentialwärmegleichung (oder die Wärmediffusionsgleichung) wird wie folgt geschrieben:

f r a c p a r t i e l l e s T (x, t) p a r t i e l l e s t + D f r a c p a r t i e l l e s^{2} U (x, t) p a r t i e l l e s x^{2} = p h i (T, x, t)

$\ frac {\ partielles T (x, t)} {\ partielles t} + D \ frac {\ partielles ^ 2 U (x, t)} {\ partielles x ^ 2} = \ phi (T, x, t )$

Dies ist eine parabolische Gleichung, die die erste Ableitung in Bezug auf die Zeit t und die zweite in Bezug auf die Raumkoordinate x enthält. Es beschreibt die Temperaturdynamik beispielsweise eines Kühl- oder Heizmetallstabs (die Funktion T beschreibt das Temperaturprofil entlang der x-Koordinate entlang des Stabes). Der Koeffizient D wird als Wärmeleitfähigkeitskoeffizient (Diffusion) bezeichnet. Sie kann entweder konstant sein oder sowohl explizit von den Koordinaten als auch von der gewünschten Funktion D (t, x, T) selbst abhängen.

Betrachten Sie die lineare Gleichung (Diffusionskoeffizient und Wärmequellen sind temperaturunabhängig). Die Differenznäherung einer Differentialgleichung unter Verwendung des expliziten bzw. des impliziten Euler-Schemas:

f r a c T_{i, n + 1} - T_{i, n} t a u = D f r a c T_{i - 1, n} - 2 T_{i, n} + T_{i + 1, n} D e l t a^{2} + p h i_{i, n} f r a c T_{i, n + 1} - T_{i, n} t a u = D f r a c T_{i - 1, n + 1} - 2 T_{i, n + 1} + T_{i + 1, n + 1} D e l t a^{2} + p h i_{i, n}

$\ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ {i-1, n} -2T_ {i, n} + T_ {i + 1 , n}} {\ Delta ^ 2} + \ phi_ {i, n} \\ \ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ { i-1, n + 1} -2T_ {i, n + 1} + T_ {i + 1, n + 1}} {\ Delta ^ 2} + \ phi_ {i, n}$

 δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # -     startcond = x-> δ(x-0.45) - δ(x-0.55) #   bordrcond = x-> 0. #    D(u) = 1 #   Φ(u) = 0 #    #      LaTex    Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] #         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )

Ergebnis

Wir verwenden das implizite Schema und die Sweep-Methode

 function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

Schaltungsvergleich

Nichtlineare Wärmegleichung

Viel interessantere Lösungen können für die nichtlineare Wärmegleichung erhalten werden, beispielsweise mit einer nichtlinearen Wärmequelle $\ phi (x, T) = 10 ^ 3 (T-T ^ 3)$ . Wenn Sie es in dieser Form einstellen, erhalten Sie eine Lösung in Form von Wärmefronten, die sich auf beiden Seiten der primären Heizzone ausbreiten

 Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")

Thermofront

Noch unerwartetere Lösungen sind auch bei Nichtlinearität des Diffusionskoeffizienten möglich. Zum Beispiel, wenn Sie nehmen $D (x, T) = T ^ 2$ a $\ phi (x, T) = 10 ^ 3T ^ {3.5}$ Dann kann man den Effekt der Verbrennung des Mediums beobachten, der im Bereich seiner primären Erwärmung lokalisiert ist (S-Verbrennungsmodus „mit Exazerbation“).
Gleichzeitig werden wir überprüfen, wie unser implizites Schema mit der Nichtlinearität beider Quellen und dem Diffusionskoeffizienten funktioniert

 D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") #      plot(p1, p2)

S-Modus

Wellengleichung

Hyperbolische Wellengleichung

f r a c p a r t i e l l^{2} U (x, t) p a r t i e l l t^{2} = c^{2} f r a c p a r t i e l l^{2} U (x, t) p a r t i e l l x^{2}

$\ frac {\ partiell ^ 2 U (x, t)} {\ partiell t ^ 2} = c ^ 2 \ frac {\ partiell ^ 2 U (x, t)} {\ partiell x ^ 2}$

beschreibt eindimensionale lineare Wellen ohne Dispersion. Zum Beispiel Schwingungen einer Saite, Schall in einer Flüssigkeit (Gas) oder elektromagnetische Wellen in einem Vakuum (im letzteren Fall sollte die Gleichung in Vektorform geschrieben werden).

Das einfachste Differenzschema, das sich dieser Gleichung annähert, ist ein explizites Fünf-Punkte-Schema

f r a c U_{i}^{n + 1} - 2 U_{i}^{n} + U_{i}^{n - 1} t a u^{2} = c^{2} f r a c U_{i + 1}^{n} - 2 U_{i}^{n} + U_{i - 1}^{n} h^{2} x_{i} = i h, t_{n} = t a u

$\ frac {U ^ {n + 1} _i-2U ^ {n} _i + U ^ {n-1} _i} {\ tau ^ 2} = c ^ 2 \ frac {U ^ n_ {i + 1} -2U ^ n_i + U ^ n_ {i-1}} {h ^ 2} \\ x_i = ih, \, t_n = \ tau$

Dieses als "Kreuz" bezeichnete Schema hat eine zweite zeitliche Genauigkeit und räumliche Koordinatenordnung und ist zeitlich dreischichtig.

 #     ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) #    ϕ(x) = 0 c = x -> 1 #     function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] #      u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); #     fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; #     K = 40; #    a = 0.1; #    L = 1; #   T = 1; #   t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) #    plot(X, U[:,1]) plot!(X, U[:,40])

Ergebnis

Um eine Oberfläche zu erstellen, verwenden wir PyPlot als Plots-Umgebung, aber direkt:

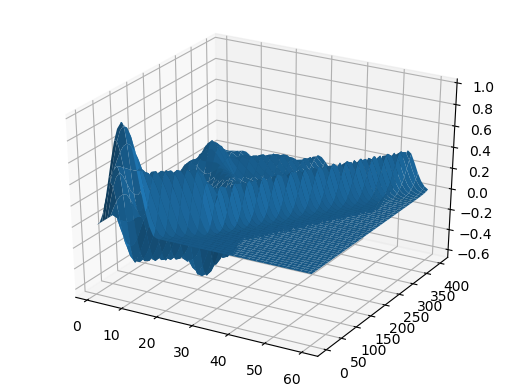
Oberflächendiagramm

 using PyPlot surf(t, X, U)

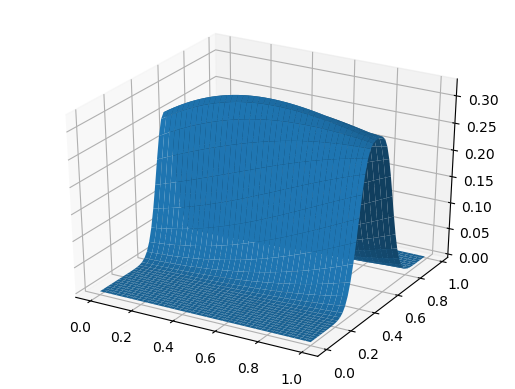
Und zum Nachtisch breitet sich die Welle mit einer Geschwindigkeit aus, die von der Koordinate abhängt:

 ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=("  ", (0, 1.5), 0:0.5:2) )

Ergebnis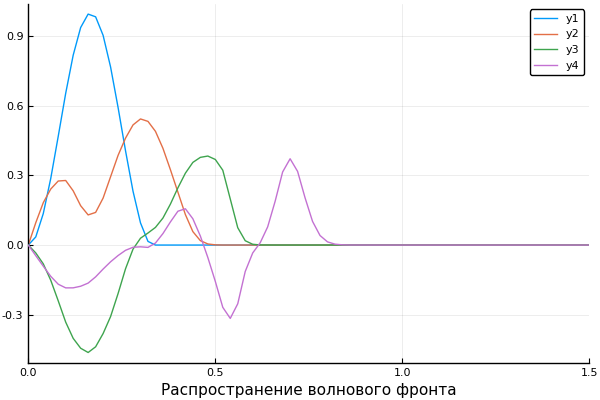

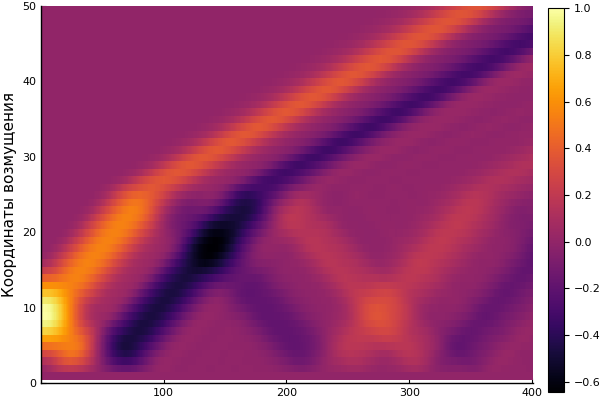
 U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] #    surf(U2) #

heatmap(U, yaxis=(" ", (0, 50), 0:10:50))

Genug für heute. Für eine detailliertere Überprüfung:
PyPlot-Link zu Github , andere Beispiele für die Verwendung von Plots als Umgebung und ein gutes russischsprachiges Memo von Julia .

Julia und partielle Differentialgleichungen

Trage Gleichung

Nichtlineare Übertragung

Wärmegleichung

Nichtlineare Wärmegleichung

Wellengleichung

More articles: