Ein Variations-Auto-Encoder (Auto-Encoder) ist ein generatives Modell, das lernt, Objekte in einem bestimmten verborgenen Raum anzuzeigen.

Haben Sie sich jemals gefragt, wie ein VAE-Modell (Variational Auto-Encoder) funktioniert? Möchten Sie wissen, wie VAE neue Beispiele wie den Datensatz generiert, für den es trainiert wurde? Nachdem Sie diesen Artikel gelesen haben, erhalten Sie ein theoretisches Verständnis der internen Funktionsweise von VAE und können es auch selbst implementieren. Dann werde ich den funktionierenden VAE-Code zeigen, der auf einer Reihe von handgeschriebenen Ziffern trainiert wurde, und wir werden Spaß haben und neue Ziffern generieren!

Generative Modelle

VAE ist ein generatives Modell - es schätzt die Wahrscheinlichkeitsdichte (PDF) von Trainingsdaten. Wenn ein solches Modell in natürlichen Bildern trainiert wird, weist es dem Bild des Löwen einen hohen Wahrscheinlichkeitswert und dem Bild von zufälligem Bullshit einen niedrigen Wert zu.

Das VAE-Modell kann auch Beispiele aus trainierten PDF-Dateien entnehmen, was der coolste Teil ist, da neue Beispiele ähnlich dem Originaldatensatz generiert werden können!

Ich werde VAE mit dem handschriftlichen Nummernsatz MNIST erklären . Die Eingabedaten für das Modell sind Bilder im Format $$$\ mathbb {R} ^ {28 × 28}$. Das Modell sollte die Wahrscheinlichkeit bewerten, wie sehr die Eingabe wie eine Ziffer aussieht.

Bildmodellierungsaufgabe

Die Interaktion zwischen Pixeln ist eine schwierige Aufgabe. Wenn die Pixel unabhängig voneinander sind, müssen Sie das PDF jedes Pixels unabhängig voneinander untersuchen, was einfach ist. Die Auswahl ist ebenfalls einfach - wir nehmen jedes Pixel einzeln.

In digitalen Bildern gibt es jedoch deutliche Abhängigkeiten zwischen den Pixeln. Wenn Sie den Anfang der vier auf der linken Hälfte sehen, werden Sie sehr überrascht sein, wenn die rechte Hälfte die Vervollständigung von Null ist. Aber warum?..

Versteckter Raum

Sie wissen, dass jedes Bild eine Nummer hat. Eingang zu $$$\ mathbb {R} ^ {28 × 28}$enthält diese Informationen eindeutig nicht. Aber es muss irgendwo sein ... Dieses "irgendwo" ist ein versteckter Raum.



Sie können sich verborgenen Raum als vorstellen $$$\ mathbb {R} ^ {k}$wo jeder Vektor enthält $$$k$Informationen, die zum Rendern eines Bildes benötigt werden. Angenommen, die erste Dimension enthält eine Zahl, die durch eine Ziffer dargestellt wird. Die zweite Dimension kann die Breite sein. Der dritte ist der Winkel und so weiter.

Wir können uns den Prozess des Zeichnens einer Person in zwei Schritten vorstellen. Zunächst bestimmt eine Person - bewusst oder nicht - alle Attribute der Nummer, die angezeigt werden soll. Als nächstes werden diese Entscheidungen in Striche auf Papier umgewandelt.

VAE versucht, diesen Prozess zu simulieren: für ein bestimmtes Bild $$$x$wir wollen mindestens einen versteckten Vektor finden, der ihn beschreiben kann; ein Vektor enthält Anweisungen zum Erzeugen $$$x$. Wenn wir es nach der Formel der Gesamtwahrscheinlichkeit formulieren, erhalten wir $$$P (x) = \ int P (x | z) P (z) dz$.

Lassen Sie uns einen vernünftigen Sinn in diese Gleichung setzen:

• Integral bedeutet, dass Kandidaten in allen verborgenen Räumen gesucht werden müssen.
• Für jeden Kandidaten $$$z$wir stellen die frage: ist es möglich zu generieren $$$x$mit Anweisungen $$$z$? Ist es groß genug? $$$P (x | z)$? Zum Beispiel wenn $$$z$codiert Informationen über die Ziffer 7, dann ist Bild 8 nicht möglich. Bild 1 ist jedoch akzeptabel, da 1 und 7 ähnlich sind.
• Wir haben einen guten gefunden. $$$z$? Großartig! Aber warte eine Sekunde ... wie viel kostet es? $$$z$wahrscheinlich? $$$P (z)$groß genug? Betrachten Sie das Bild der invertierten Zahl 7. Eine ideale Übereinstimmung wäre ein versteckter Vektor, der die Ansicht 7 beschreibt, in der die Winkelgröße auf 180 ° eingestellt ist. Jedoch solche $$$z$Dies ist unwahrscheinlich, da Zahlen normalerweise nicht in einem Winkel von 180 ° geschrieben werden.

Das Ziel des VAE-Trainings ist die Maximierung $$$P (x)$. Wir werden modellieren $$$P (x | z)$unter Verwendung einer mehrdimensionalen Gaußschen Verteilung $$$\ mathcal {N} (f (z), \ sigma ^ 2 \ cdot I)$.

$$$f (z)$modelliert mit einem neuronalen Netzwerk. $$$\ sigma$Ist ein Hyperparameter zum Multiplizieren der Identitätsmatrix $$$I$.

Denken Sie daran $$$f$- Dies wird verwendet, um neue Bilder mit einem trainierten Modell zu generieren. Das Überlappen einer Gaußschen Verteilung dient nur zu Bildungszwecken. Wenn wir die Dirac-Delta-Funktion nehmen (d. H. Deterministisch $$$x = f (z)$), dann können wir das Modell nicht mit Gradientenabstieg trainieren!

Die Wunder des verborgenen Raumes

Der Hidden-Space-Ansatz hat zwei große Probleme:

1. Welche Informationen enthält jede Dimension? Einige Dimensionen können sich auf abstrakte Elemente beziehen, z. B. den Stil. Selbst wenn es einfach wäre, alle Dimensionen zu interpretieren, möchten wir dem Datensatz keine Beschriftungen zuweisen. Dieser Ansatz lässt sich nicht auf andere Datensätze skalieren.
2. Versteckter Raum kann verwirrt werden, wenn eine Korrelation zwischen Dimensionen besteht. Beispielsweise kann eine sehr schnell gezeichnete Zahl gleichzeitig zum Auftreten von eckigen und dünneren Strichen führen. Das Definieren dieser Abhängigkeiten ist schwierig.

Tiefes Lernen hilft

Es stellt sich heraus, dass jede Verteilung durch Anwenden einer ziemlich komplexen Funktion auf die mehrdimensionale Standard-Gauß-Verteilung erzeugt werden kann.

Wählen Sie $$$P (z)$als standardmäßige mehrdimensionale Gaußsche Verteilung. So modelliert durch ein neuronales Netzwerk $$$f$kann in zwei Phasen unterteilt werden:

1. Die ersten Ebenen bilden die Gaußsche Verteilung in die wahre Verteilung über den verborgenen Raum ab. Wir können die Messungen nicht interpretieren, aber es spielt keine Rolle.
2. Nachfolgende Ebenen werden aus dem verborgenen Raum in angezeigt $$$P (x | z)$.

Wie trainieren wir dieses Biest?

Formel für $$$P (x)$unlöslich, daher approximieren wir es nach der Monte-Carlo-Methode:

1. Auswahl $$$\ {z_i \} _ {i = 1} ^ n$ vom vorherigen $$$P (z)$
2. Annäherung mit $$$P (x) \ approx \ frac {1} {n} \ sum_ {i = 1} ^ n P (x | z_i)$

Großartig! Probieren Sie einfach viel anderes aus $$$z$und starte die Bug Propagation Party!

Leider seit $$$x$Sehr mehrdimensional, um eine vernünftige Annäherung zu erhalten, sind viele Proben erforderlich. Ich meine, wenn du es versuchst $$$z$Wie hoch sind dann die Chancen, ein Bild zu erhalten, das ungefähr so ​​aussieht? $$$x$? Dies erklärt übrigens warum $$$P (x | z)$muss jedem möglichen Bild einen positiven Wahrscheinlichkeitswert zuweisen, sonst kann das Modell nicht lernen: Abtastung $$$z$führt zu einem Bild, das sich mit ziemlicher Sicherheit von unterscheidet $$$x$und wenn die Wahrscheinlichkeit 0 ist, können sich die Gradienten nicht ausbreiten.

Wie kann man dieses Problem lösen?

Schneiden Sie den Weg!

Die meisten Proben $$$z$Von der Auswahl zu wird nichts hinzugefügt $$$P (x)$- Sie sind zu weit über ihre Grenzen hinaus. Wenn Sie im Voraus wussten, woher Sie sie nehmen sollten ...

Kann eintreten $$$Q (z | x)$. Gegeben $$$Q$wird trainiert, um hohe Wahrscheinlichkeitswerte zuzuweisen $$$z$das sind wahrscheinlich zu generieren $$$x$. Jetzt können Sie eine Bewertung mit der Monte-Carlo-Methode vornehmen und dabei viel weniger Proben entnehmen $$$Q$.

Leider entsteht ein neues Problem! Anstatt zu maximieren $$$P (x) = \ int P (x | z) P (z) dz = \ mathbb {E} _ {z \ sim P (z)} P (x | z)$wir maximieren $$$\ mathbb {E} _ {z \ sim Q (z | x)} P (x | z)$. Wie hängen sie miteinander zusammen?

Variationsschlussfolgerung

Die Variationsschlussfolgerung ist das Thema eines separaten Artikels, daher werde ich hier nicht im Detail darauf eingehen. Ich kann nur sagen, dass diese Verteilungen durch diese Gleichung zusammenhängen:

$$

$$log P (X) - \ mathcal {KL} [Q (z | x) || P (z | x)] = \ mathbb {E} _ {z \ sim Q (z | x)} [log P (x | z)] - \ mathcal {KL} [Q (z | x) || P (z)]$$

$$$\ mathcal {KL}$ist der Kullback-Leibler-Abstand , der die Ähnlichkeit der beiden Verteilungen intuitiv bewertet.

In einem Moment werden Sie sehen, wie Sie die rechte Seite der Gleichung maximieren können. In diesem Fall wird auch die linke Seite maximiert:

• $$$P (x)$maximiert.
• wie weit $$$Q (z | x)$von $$$P (z | x)$- real a priori unbekannt - wird minimiert.

Die Bedeutung der rechten Seite der Gleichung ist, dass wir hier Spannung haben:

1. Einerseits wollen wir maximieren, wie gut $$$x$muss entschlüsselt werden von $$$z \ sim Q$.
2. Auf der anderen Seite wollen wir $$$Q (z | x)$( Encoder ) war ähnlich wie der vorherige $$$P (z)$(mehrdimensionale Gaußsche Verteilung). Dies kann als Regularisierung angesehen werden.

Minimierung der Divergenz $$$\ mathcal {KL}$leicht mit der richtigen Auswahl von Distributionen durchgeführt. Wir werden simulieren $$$Q (z | x)$als neuronales Netzwerk, dessen Ausgabe die Parameter einer mehrdimensionalen Gaußschen Verteilung sind:

• Durchschnitt $$$\ mu_Q$
• diagonale Kovarianzmatrix $$$\ Sigma_Q$

Dann Divergenz $$$\ mathcal {KL}$wird analytisch lösbar, was für uns (und für Gradienten) großartig ist.

Der Decoderteil ist etwas komplizierter. Auf den ersten Blick möchte ich feststellen, dass dieses Problem mit der Monte-Carlo-Methode nicht lösbar ist. Aber die Probe $$$z$von $$$Q$Gradienten können sich nicht ausbreiten $$$Q$, weil die Auswahl keine differenzierbare Operation ist. Dies ist ein Problem, da seitdem die Gewichte der Schichten ausgegeben werden $$$\ Sigma_Q$und $$$\ mu_Q$.

Neuer Parametrisierungstrick

Wir können ersetzen $$$Q$deterministische parametrisierte Transformation einer nichtparametrischen Zufallsvariablen:

1. Eine Stichprobe aus der Standard-Gauß-Verteilung (ohne Parameter).
2. Multiplizieren Sie die Probe mit der Quadratwurzel $$$\ Sigma_Q$.
3. Zum Ergebnis hinzufügen $$$\ mu_Q$.

Als Ergebnis erhalten wir eine Verteilung gleich $$$Q$. Jetzt kommt die Abrufoperation von der Standard-Gauß-Verteilung. Folglich können sich Gradienten ausbreiten $$$\ Sigma_Q$und $$$\ mu_Q$seitdem sind dies deterministische Pfade.

Ergebnis? Das Modell kann lernen, wie die Parameter angepasst werden $$$Q$: Sie wird sich auf das Gute konzentrieren $$$z$die produzieren können $$$x$.

Alles zusammenfügen

Das VAE-Modell kann schwierig zu verstehen sein. Wir haben hier viel Material untersucht, das schwer verdaulich ist.

Lassen Sie mich alle Schritte zur Implementierung von VAE zusammenfassen.



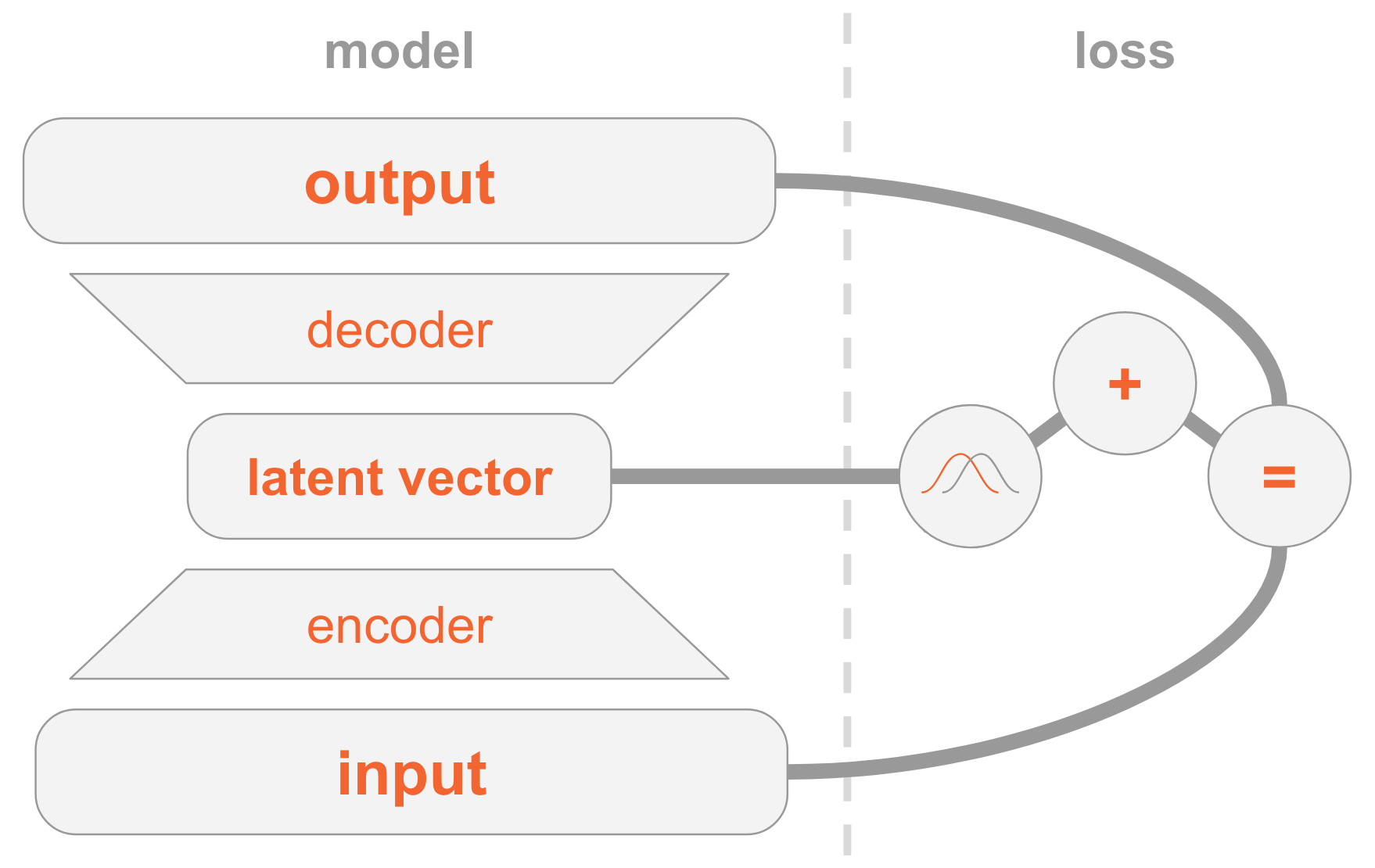
Links haben wir eine Modelldefinition:

1. Das Eingabebild wird über das Encodernetzwerk übertragen.
2. Der Encoder liefert Verteilungsparameter $$$Q (z | x)$.
3. Versteckter Vektor $$$z$entnommen aus $$$Q (z | x)$. Wenn der Encoder gut trainiert ist, dann in den meisten Fällen $$$z$eine Beschreibung enthalten $$$x$.
4. Decoder decodiert $$$z$in das Bild.

Auf der rechten Seite haben wir eine Verlustfunktion:

1. Wiederherstellungsfehler: Die Ausgabe sollte der Eingabe ähnlich sein.
2. $$$Q (z | x)$sollte der vorherigen ähnlich sein, dh einer mehrdimensionalen Standardnormalverteilung.

Um neue Bilder zu erstellen, können Sie den ausgeblendeten Vektor direkt aus der vorherigen Verteilung auswählen und in ein Bild dekodieren.

Arbeitscode

Jetzt werden wir VAE genauer untersuchen und den Arbeitscode betrachten. Sie werden alle technischen Details verstehen, die zur Implementierung von VAE erforderlich sind. Als Bonus zeige ich Ihnen einen interessanten Trick: Wie Sie einigen Dimensionen des verborgenen Vektors spezielle Rollen zuweisen, damit das Modell Bilder der angegebenen Zahlen generiert.

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline 

Ich erinnere Sie daran, dass Modelle auf MNIST trainiert werden - eine Reihe handgeschriebener Zahlen. Eingabebilder haben das Format $$$\ mathbb {R} ^ {28 × 28}$.

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10 

Als nächstes definieren wir Hyperparameter.

Spielen Sie mit verschiedenen Werten, um eine Vorstellung davon zu bekommen, wie sie sich auf das Modell auswirken.

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 } 

Modell

Das Modell besteht aus drei Subnetzen:

1. Gets $$$x$(Bild), codiert es in eine Distribution $$$Q (z | x)$im verborgenen Raum.
2. Gets $$$z$dekodiert es im versteckten Raum (Codedarstellung des Bildes) in das entsprechende Bild $$$f (z)$.
3. Gets $$$x$und bestimmt die Zahl durch Vergleich mit der 10-dimensionalen Schicht, wobei der i-te Wert die Wahrscheinlichkeit der i-ten Zahl enthält.

Die ersten beiden Subnetze bilden die Grundlage für reine VAE.

Die dritte ist eine Hilfsaufgabe , bei der einige der verborgenen Dimensionen verwendet werden, um die im Bild gefundenen Zahlen zu codieren. Ich werde erklären, warum: Wir haben zuvor besprochen, dass es uns egal ist, welche Informationen jede Dimension des verborgenen Raums enthält. Ein Modell kann lernen, alle Informationen zu codieren, die es für seine Aufgabe als wertvoll erachtet. Da wir mit dem Datensatz vertraut sind, kennen wir die Bedeutung der Dimension, die den Typ der Ziffer (d. H. Ihren numerischen Wert) enthält. Und jetzt wollen wir dem Modell helfen, indem wir ihr diese Informationen zur Verfügung stellen.

Für einen bestimmten Zifferntyp codieren wir ihn direkt, dh wir verwenden einen Vektor der Größe 10. Diese zehn Zahlen sind einem versteckten Vektor zugeordnet. Wenn Sie diesen Vektor in ein Bild decodieren, verwendet das Modell digitale Informationen.

Es gibt zwei Möglichkeiten, um direkt codierende Vektormodelle bereitzustellen:

1. Fügen Sie es als Eingabe zum Modell hinzu.
2. Fügen Sie es als Bezeichnung hinzu, damit das Modell die Prognose selbst berechnet: Wir fügen ein weiteres Subnetz hinzu, das einen 10-dimensionalen Vektor vorhersagt, wobei die Verlustfunktion die Kreuzentropie mit dem erwarteten Vorwärtscodierungsvektor ist.

Wählen Sie die zweite Option. Warum? Nun, beim Testen können Sie das Modell auf zwei Arten verwenden:

1. Geben Sie das Bild als Eingabe an und zeigen Sie einen ausgeblendeten Vektor an.
2. Geben Sie einen ausgeblendeten Vektor als Eingabe an und generieren Sie ein Bild.

Da wir die erste Option unterstützen möchten, können wir dem Modell keine Ziffer als Eingabe geben, da wir sie beim Testen nicht wissen möchten. Daher muss das Modell lernen, es vorherzusagen.

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits 

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers']) 

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss) 

Schulung

Wir werden ein Modell zur Optimierung von zwei Verlustfunktionen - VAE und Klassifizierung - unter Verwendung von SGD trainieren.

Am Ende jeder Epoche wählen wir versteckte Vektoren aus und decodieren sie in Bilder, um visuell zu beobachten, wie sich die generative Kraft des Modells gegenüber Epochen verbessert. Die Probenahmemethode ist wie folgt:

1. Legen Sie explizit die Dimensionen fest, die zur Klassifizierung nach der zu generierenden Ziffer verwendet werden. Wenn wir beispielsweise ein Bild der Nummer 2 erstellen möchten, legen wir die Maße fest $$$[0010000000]$.
2. Wählen Sie zufällig aus anderen Dimensionen der mehrdimensionalen Normalverteilung. Dies sind die Werte für die verschiedenen Zahlen, die in dieser Ära generiert werden. So bekommen wir eine Vorstellung davon, was in anderen Dimensionen codiert ist, zum Beispiel im Handschriftstil.

Die Bedeutung von Schritt 1 besteht darin, dass das Modell nach der Konvergenz in der Lage sein sollte, die Figur im Eingabebild anhand dieser Messeinstellungen zu klassifizieren. Sie werden jedoch auch in der Decodierungsphase verwendet, um ein Bild zu erstellen. Das heißt, das Decoder-Subnetz weiß: Wenn die Messungen der Nummer 2 entsprechen, sollte es ein Bild mit dieser Nummer erzeugen. Wenn wir die Messungen manuell auf die Zahl 2 einstellen, erhalten wir daher ein generiertes Bild dieser Figur.

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples) 

Lassen Sie uns überprüfen, ob beide Verlustfunktionen gut aussehen, dh abnehmen:

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout() 

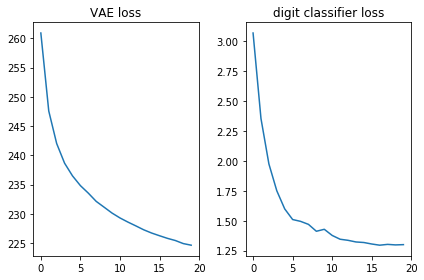
Lassen Sie uns außerdem die generierten Bilder anzeigen und prüfen, ob das Modell wirklich Bilder mit handschriftlichen Zahlen erstellen kann:

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples) 

Fazit

Es ist schön zu sehen, dass ein einfaches Direktvertriebsnetz (ohne ausgefallene Windungen) in nur 20 Epochen wunderschöne Bilder erzeugt. Das Modell lernte schnell, spezielle Messungen für Zahlen zu verwenden: In der 9. Ära sehen wir bereits die Folge von Zahlen, die wir zu generieren versuchten.

Jede Epoche verwendete unterschiedliche Zufallswerte für andere Dimensionen, so dass der Stil zwischen den Epochen unterschiedlich ist, aber in ihnen ähnlich ist: zumindest in einigen. Zum Beispiel sind im 18. alle Zahlen dicker als im 20 ..

Anmerkungen

Der Artikel basiert auf meiner Erfahrung und den folgenden Quellen:

• Variationsschlussfolgerung und tiefes Lernen: eine neue Synthese
• Variation Auto Coder Guide