MIT-Kurs "Computer Systems Security". Vorlesung 16: „Seitenkanalangriffe“, Teil 1

Massachusetts Institute of Technology. Vorlesung # 6.858. "Sicherheit von Computersystemen." Nikolai Zeldovich, James Mickens. 2014 Jahr

Computer Systems Security ist ein Kurs zur Entwicklung und Implementierung sicherer Computersysteme. Die Vorträge behandeln Bedrohungsmodelle, Angriffe, die die Sicherheit gefährden, und Sicherheitstechniken, die auf jüngsten wissenschaftlichen Arbeiten basieren. Zu den Themen gehören Betriebssystemsicherheit, Funktionen, Informationsflussmanagement, Sprachsicherheit, Netzwerkprotokolle, Hardwaresicherheit und Sicherheit von Webanwendungen.

Vorlesung 1: „Einführung: Bedrohungsmodelle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 2: „Kontrolle von Hackerangriffen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 3: „Pufferüberläufe: Exploits und Schutz“ Teil 1 / Teil 2 / Teil 3
Vorlesung 4: „Trennung von Privilegien“ Teil 1 / Teil 2 / Teil 3
Vorlesung 5: „Woher kommen Sicherheitssysteme?“ Teil 1 / Teil 2
Vorlesung 6: „Chancen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 7: „Native Client Sandbox“ Teil 1 / Teil 2 / Teil 3
Vorlesung 8: „Netzwerksicherheitsmodell“ Teil 1 / Teil 2 / Teil 3
Vorlesung 9: „Sicherheit von Webanwendungen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 10: „Symbolische Ausführung“ Teil 1 / Teil 2 / Teil 3
Vorlesung 11: „Ur / Web-Programmiersprache“ Teil 1 / Teil 2 / Teil 3
Vorlesung 12: Netzwerksicherheit Teil 1 / Teil 2 / Teil 3
Vorlesung 13: „Netzwerkprotokolle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 14: „SSL und HTTPS“ Teil 1 / Teil 2 / Teil 3
Vorlesung 15: „Medizinische Software“ Teil 1 / Teil 2 / Teil 3
Vorlesung 16: „Seitenkanalangriffe“ Teil 1 / Teil 2 / Teil 3

Ok Leute, lasst uns anfangen. Daher werden wir heute über Angriffe über Seitenkanäle sprechen, ein häufiges Problem, das allen Arten von Systemen innewohnt. Im weitesten Sinne treten Angriffe über den Seitenkanal in einer Situation auf, in der Sie nicht glauben, dass einige Informationen Informationen über Ihr System preisgeben können.



In der Regel verfügen Sie über mehrere Komponenten, die eine Verbindung zwischen dem Benutzer und dem Server herstellen. Gleichzeitig denken Sie, dass Sie über alles Bescheid wissen, was durch diese Verbindung zwischen zwei Teilnehmern verläuft, dass Sie über alle Bits Bescheid wissen, die Benutzer und Server miteinander austauschen, und dies ist sicher. Es kommt jedoch häufig vor, dass einige Informationen immer noch vom Benutzer oder Server offengelegt werden. Das in den Materialien der heutigen Vorlesung erwähnte Beispiel beschreibt eine Situation, in der die Synchronisation von Nachrichten zwischen dem Benutzer und dem Server einige zusätzliche Informationen enthüllt, die Sie nicht kennen würden, indem Sie nur den Bitstrom zwischen diesen Teilnehmern beobachten.

Tatsächlich gibt es eine viel größere Klasse von Seitenkanälen, über die Sie sich Sorgen machen können. Die Menschen erfuhren bereits in den 40er Jahren vom Auftreten von Seitenkanälen, als sie entdeckten, dass die Teletypelektronik Radiofrequenzstrahlung aussendet, wenn Sie Zeichen auf einem Teletyp eingeben. In diesem Fall können Sie einfach das Oszilloskop daneben platzieren und beobachten, wie sich die Frequenz des Funksignals ändert, je nachdem, welches Symbol der Fernschreiber druckt. Daher ist HF-Strahlung ein klassisches Beispiel für einen Seitenkanal, der Sie beunruhigt.

Es gibt viele andere Beispiele, die von Menschen bemerkt werden, wie zum Beispiel den Stromverbrauch. Dies ist ein weiterer Seitenkanal, über den Sie sich Sorgen machen können, da Ihr Computer je nach Berechnung eine andere Energiemenge verbraucht.



Ein Beispiel für einen Seitenkanal ist Ton, aufgrund dessen auch ein Informationsverlust möglich ist. Beispielsweise hören die Benutzer dem Drucker zu und können anhand der von ihnen erzeugten Geräusche erkennen, welche Zeichen gedruckt werden. Dies ist besonders einfach für Nadeldrucker, die beim Drucken sehr störende Geräusche erzeugen.

Im Allgemeinen ist dies etwas zum Nachdenken. In einem Vortrag am Montag erwähnte Kevin auch einige interessante Nebenkanäle, mit denen er sich in seiner Forschung befasst. Aber wir werden uns den spezifischen Seitenkanal ansehen, den David Bramley und Dan Bone studiert haben. In ihrer vor etwa 10 Jahren veröffentlichten Arbeit schreiben sie, dass sie den kryptografischen Schlüssel des Apache-Webservers extrahieren konnten, indem sie das Timing verschiedener Antworten auf verschiedene Eingabepakete eines feindlichen Clients maßen. In diesem speziellen Fall „suchten“ sie nach einem kryptografischen Schlüssel. Tatsächlich zielen viele Angriffe über den Seitenkanal teilweise auf kryptografische Schlüssel ab, da es ziemlich schwierig ist, eine große Datenmenge über einen solchen Kanal zu erhalten. Und kryptografische Schlüssel sind eine der Situationen, in denen eine kleine Anzahl von Bits ausgegeben wird, dh während eines Angriffs können Angreifer etwa 200 bis 256 Bits an Informationen extrahieren. Aber nur basierend auf diesen 200 Bits können sie den kryptografischen Schlüssel dieses Webservers knacken.

Wenn Sie versuchen, in eine Datenbank mit Sozialversicherungsnummern zu gelangen, müssen Sie viele Informationen daraus „zusammenführen“. Aus diesem Grund konzentrieren sich die meisten Seitenkanalangriffe darauf, kleine Geheimnisse wie kryptografische Schlüssel oder Passwörter zu erhalten. Im Allgemeinen gilt dies jedoch für viele andere Situationen.

In den Vorlesungsunterlagen wird eine andere coole Sache beschrieben - das alles kann über das Netzwerk erfolgen. Sie haben wahrscheinlich festgestellt, dass sie viel sorgfältige Arbeit leisten mussten, um diese kleinsten Unterschiede in der Zeitinformation zu erkennen. Jede an den Server gesendete Anfrage unterschied sich von einer anderen Anfrage um 1-2 Mikrosekunden, was eine sehr kurze Zeitspanne ist. Daher sollten Sie sehr vorsichtig sein, da unsere Netzwerke es uns nicht erlauben, einen solchen vorübergehenden Unterschied zu erkennen und festzustellen, dass der Server Ihre Anfrage 1-2 Mikrosekunden länger verarbeitet hat, als er sollte.



Infolgedessen war nicht klar, ob ein solcher Angriff in einem sehr "lauten" Netzwerk organisiert werden konnte, da nützliche Informationen vom Geräuschpegel getrennt werden sollten. Diese Leute waren unter den ersten, die zeigten, dass Sie dies wirklich über ein Ethernet-Netzwerk mit einem Server an einem Ende des Netzwerks und einem Client am anderen Ende tun können. Sie haben bewiesen, dass es tatsächlich möglich ist, diese Unterschiede teilweise durch Mittelwertbildung, teilweise durch andere Tricks zu messen.
Der Plan für den Rest dieser Vorlesung lautet wie folgt: Zuerst gehen wir auf die Details des kryptografischen RSA-Algorithmus für öffentliche Schlüssel ein, den diese Leute verwendet haben. Wir werden es nicht unter Sicherheitsgesichtspunkten bewerten, aber wir werden sehen, wie es implementiert wird, da die Implementierung des Algorithmus für die Verwendung des Seitenkanals entscheidend ist.

Bramley und Bone untersuchten die verschiedenen Implementierungsdetails, um zu verstehen, wann bestimmte Dinge schneller oder langsamer abliefen. Zuerst müssen wir herausfinden, wie das RSA-Kryptosystem implementiert ist, und dann werden wir zurückgehen und herausfinden, wie alle diese in RSA verfügbaren Strukturen angegriffen werden können.

Beginnen wir mit einer hochrangigen RSA-Überprüfung. RSA ist ein ziemlich weit verbreitetes Kryptosystem mit öffentlichem Schlüssel. Wir haben diese Leute vor ein paar Wochen erwähnt, als wir über Zertifikate gesprochen haben. Jetzt werden wir sehen, wie es tatsächlich funktioniert.

In der Regel gibt es drei Dinge, über die Sie sich Sorgen machen müssen: Schlüsselgenerierung, Verschlüsselung und Entschlüsselung. In RSA können Sie einen Schlüssel erstellen, indem Sie zwei große Primzahlen auswählen und diese mit p und q bezeichnen. In ihrem Artikel schreiben diese Leute über p und q mit einer Größe von jeweils 512 Bit. Dies wird normalerweise als 1024-Bit-RSA bezeichnet, da das Produkt dieser Primzahlen eine 1000-Bit-Ganzzahl ist. Heutzutage ist dies wahrscheinlich keine gute Wahl für die RSA-Schlüsselgröße, da das Brechen für Angreifer eine relativ einfache Aufgabe ist. Wenn also vor 10 Jahren 1000 Bit eine vernünftige Menge waren, sollten Sie heute beim Aufbau eines Systems einen RSA-Schlüssel mit 2000, 3000 oder sogar 4000 Bit wählen. Die RSA-Schlüsselgröße bedeutet also die Größe dieser Primzahlen.

Der Einfachheit halber werden wir dann über die Zahl n sprechen, die einfach das Produkt dieser Primzahlen n = pq ist, und diese Zahl wird als Modul bezeichnet. Nachdem wir nun wissen, wie der Schlüssel oder zumindest ein Teil des Schlüssels erstellt wird, müssen wir herausfinden, wie Nachrichten verschlüsselt und entschlüsselt werden.



Und die Art und Weise, wie wir Nachrichten verschlüsseln und entschlüsseln, basiert auf der Erhöhung der Potenz von Zahlenmodulen. Es scheint ein wenig seltsam, aber wir werden es gleich herausfinden. Wenn Sie also die Nachricht m verschlüsseln möchten, müssen Sie sie mit mod n in m ^e konvertieren. Der Wert von e ist ein Grad. In einer Sekunde werden wir herausfinden, wie man ihn wählt. So werden wir die Nachricht verschlüsseln.

Das heißt, wir nehmen diese Nachricht einfach als Ganzzahl und erheben sie zu einer Potenz. In einer Sekunde werden wir sehen, warum dies funktioniert, aber im Moment werden wir all diese verschlüsselten Nachrichten mit dem Buchstaben C kennzeichnen.

Um es dann zu entschlüsseln, müssen wir einen anderen interessanten Exponenten d finden, der es uns ermöglicht, die verschlüsselte Nachricht C zu nehmen, sie auf die Potenz d modulo n zu heben und als Ergebnis die entschlüsselte Nachricht m auf magische Weise zu erhalten.

Das allgemeine Prinzip besteht also darin, einen Exponenten zum Verschlüsseln einer Nachricht und einen anderen Exponenten zum Entschlüsseln zu verwenden.



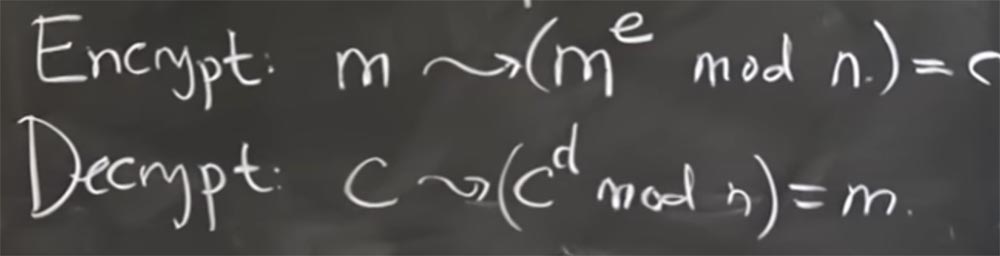
Alles in allem scheint es ein wenig schwer zu verstehen, wie wir auf diese beiden magischen Zahlen kommen werden, die uns irgendwie die ursprüngliche Botschaft zurückgeben. Aber wenn Sie sich ansehen, wie Exponentiation oder Multiplikation Modulo dieser Zahl n funktioniert, dann werden Sie alles verstehen.

Wenn wir X nehmen und es auf die Potenz erhöhen, die der Funktion φ von n entspricht, dann ist dies 1 Modulo n:

X ^{φ (n)} = 1 mod n

Diese Phi-Funktion für unsere spezielle Wahl von n ist ziemlich einfach, sie ist gleich φ = (p-1) (q-1).
Dann ist das Produkt des offenen Exponenten e, das durch den geheimen Exponenten d größer als 1, aber kleiner als φ (n) ist, gleich:

ed = ɑφ (n) +1, wobei ɑ eine Konstante ist.

Somit ist es möglich, die Nachricht korrekt zu entschlüsseln, da es einen ziemlich einfachen Algorithmus gibt, wenn Sie den Wert von φ (n) kennen, um d unter Berücksichtigung von e oder e unter Berücksichtigung von d zu berechnen.

Teilnehmerin: Ist 1 Modulo n nicht gleich 1?

Professor: Ja, ich habe hier einen Fehler gemacht, Gleichheit sollte so aussehen:

X ^{φ (n)} _{mod n} = 1 mod n, dh der Wert von X im Grad der Funktion "fi" von n modulo n ist gleich eins modulo n.

Dies bedeutet im Grunde, dass wir für RSA einen e-Wert auswählen müssen, der unser Verschlüsselungswert ist. Dann werden wir aus e d basierend auf der Formel de = 1 mod φ (n) erzeugen, daher d = 1 / e mod φ (n).



Es gibt einige euklidische Algorithmen, die Sie effektiv für diese Berechnung verwenden können. Dazu müssen Sie jedoch dieses φ (n) kennen, das eine Faktorisierung erfordert, dh die Faktorisierung unserer Zahl n in die Faktoren p und q.

RSA ist also ein System, in dem der öffentliche Schlüssel ein Paar ist: der Verschlüsselungsexponent e und die Zahl n, und das Paar d und n ist ein privater Schlüssel, der geheim gehalten wird. So kann jeder die Leistung erhöhen, um es für Sie zu verschlüsseln. Aber nur Sie kennen diesen Wert von d und können daher die Nachricht entschlüsseln. Und bis Sie die Faktorisierung dieser Faktoren P und Q oder N kennen, die gleich dem Produkt von P und Q ist, wissen Sie nicht, was φ = (p-1) (q-1) ist.



Infolgedessen ist die Berechnung dieses Wertes von d eine ziemlich schwierige Aufgabe. Darum geht es beim High-Level-RSA-Algorithmus.

Nachdem wir uns mit den Prinzipien von RSA vertraut gemacht haben, möchte ich auf zwei Dinge eingehen. Es gibt Tricks, wie man es richtig benutzt, und es gibt Fallstricke, die bei der Verwendung auftreten. Es gibt viele Möglichkeiten, Code für diese Potenzierung zu implementieren und effizient auszuführen. Dies ist eine ziemlich außergewöhnliche Aufgabe, da es sich um 1000-Bit-Ganzzahlen handelt, für die Sie nicht einfach den Multiplikationsbefehl ausführen können. Es wird wahrscheinlich lange dauern, bis diese Vorgänge abgeschlossen sind.

Daher möchte ich als erstes die verschiedenen Fallstricke von RSA erwähnen. Eine davon ist die Multiplikativität. Angenommen, wir haben 2 Nachrichten: m ₀ und m ₁ . Ich werde sie verschlüsseln und m ₀ in m ₀ ^e mod n und m1 in m ₁ ^e mod n verwandeln. Ein mögliches Problem oder vielmehr nicht unbedingt ein Problem, aber eine unangenehme Überraschung für jemanden, der RSA verwendet, ist, dass es sehr einfach ist, das Produkt m ₀ mit m ₁ zu verschlüsseln, da Sie einfach diese 2 Ziffern multiplizieren: m ₀ ^e mod n * m ₁ ^e mod n.



Wenn Sie sie multiplizieren, erhalten Sie das Produkt (m ₀ m ₁ ) ^e modulo n. Dies ist eine korrekte Verschlüsselung mit vereinfachter Verwendung von RSA für den Wert m ₀ m ₁ . Dies ist im Moment kein großes Problem, da Sie diese verschlüsselte Nachricht einfach erstellen können, sie jedoch nicht entschlüsseln können. Es ist jedoch möglich, dass Sie mit einem gemeinsamen System bestimmte Nachrichten entschlüsseln können. Das heißt, wenn Sie damit die von Ihnen erstellte Nachricht entschlüsseln können, können Sie möglicherweise durch Befolgen des umgekehrten Pfads herausfinden, welche Nachrichten m ₀ und m _{1 sind} .

Diese Tatsache sollte nicht ignoriert werden, da sie eine Reihe von Protokollen betrifft, die RSA verwenden. Es gibt eine Eigenschaft, die wir am Ende unserer Vorlesung als Abwehrmechanismus verwenden werden.

Die zweite Gefahr oder RSA-Eigenschaft, auf die Sie achten sollten, ist Determinismus oder Bestimmbarkeit. Wenn Sie in der zuvor beschriebenen elementaren Implementierung die Nachricht m nehmen und verschlüsseln und in m ^e mod n umwandeln, ist dies eine deterministische Nachrichtenfunktion. Wenn Sie es daher erneut verschlüsseln, erhalten Sie genau die gleiche Verschlüsselung.

Dies ist keine wünschenswerte Eigenschaft, denn wenn ich sehe, dass Sie eine mit RSA verschlüsselte Nachricht senden und ich wissen möchte, was es ist, kann es für mich schwierig sein, sie zu entschlüsseln. Aber ich kann verschiedene Dinge ausprobieren, wodurch ich sehe, dass Sie diese Nachricht senden.

Dann werde ich es verschlüsseln und sehen, ob Sie den gleichen verschlüsselten Text erhalten. Und wenn ja, dann werde ich herausfinden, dass Sie verschlüsselt haben. Denn alles, was ich zum Verschlüsseln einer Nachricht benötige, ist ein öffentlich zugänglicher öffentlicher Schlüssel, bei dem es sich um ein Zahlenpaar (n, e) handelt.

Das ist also nicht so toll, und Sie müssen möglicherweise mit dieser Eigenschaft vorsichtig sein, wenn Sie RSA verwenden. Daher sind solche Grundelemente nur schwer direkt zu verwenden.



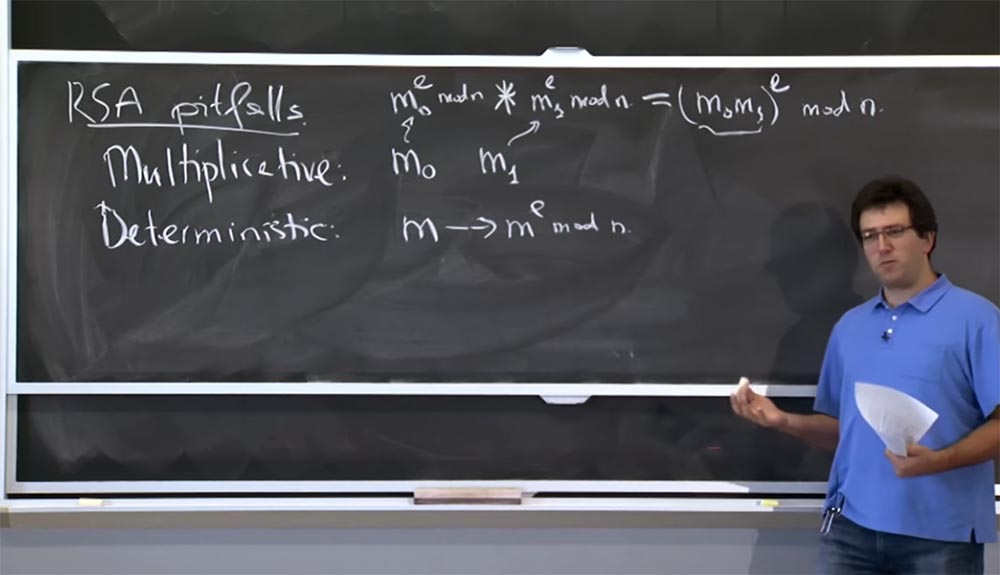
In der Praxis verschlüsseln Benutzer die Nachricht vor der Verschlüsselung auf eine bestimmte Weise, um ähnliche Probleme mit RSA zu vermeiden. Anstatt eine Nachricht direkt zu einer Macht zu erheben, nehmen sie eine Art Nachrichtenfunktion und erheben sie zu einem Machtmodul:

(f (m)) ^e mod n.

Diese heute gebräuchliche Funktion f heißt OAEP - Optimal Asymmetric Encryption with Addition. Dies ist etwas, das mit zwei interessanten Eigenschaften codiert ist.

Erstens bringt es Zufälligkeit. Sie können sich f (m) als Generierung einer 1000-Bit-Nachricht vorstellen, die Sie verschlüsseln möchten. Ein Teil dieser Nachricht ist Ihre Nachricht m hier in der Mitte dieses Rechtecks. Natürlich können Sie es beim Entschlüsseln zurückbekommen. Es gibt also zwei interessante Dinge, die Sie tun möchten: Rechts platzieren Sie eine Art Zufälligkeit, den Wert von r. Wenn Sie eine Nachricht mehrmals verschlüsseln, erhalten Sie jedes Mal unterschiedliche Ergebnisse, sodass die Verschlüsselung nicht mehr ermittelt wird.

Um diese multiplikative Eigenschaft und andere Arten von Problemen zu überwinden, haben Sie links ein Pad-Pad, das eine Sequenz vom Typ 1 0 1 0 1 0 ist. Sie können eine bessere Sequenz wählen, aber grob gesagt ist dies eine Art vorhersagbare Sequenz, die Sie fügen hier ein und stellen bei jedem Entschlüsseln der Nachricht sicher, dass diese Sequenz noch vorhanden ist. Durch die Multiplikativität werden diese Pad-Bits zerstört, und dann wird Ihnen klar, dass jemand Ihre Nachricht durcheinander gebracht und verworfen hat. Wenn diese Bits an Ort und Stelle bleiben, beweist dies, dass niemand Ihre Nachricht gefälscht hat und Sie sie empfangen können, da sie von jemandem korrekt verschlüsselt wurde.



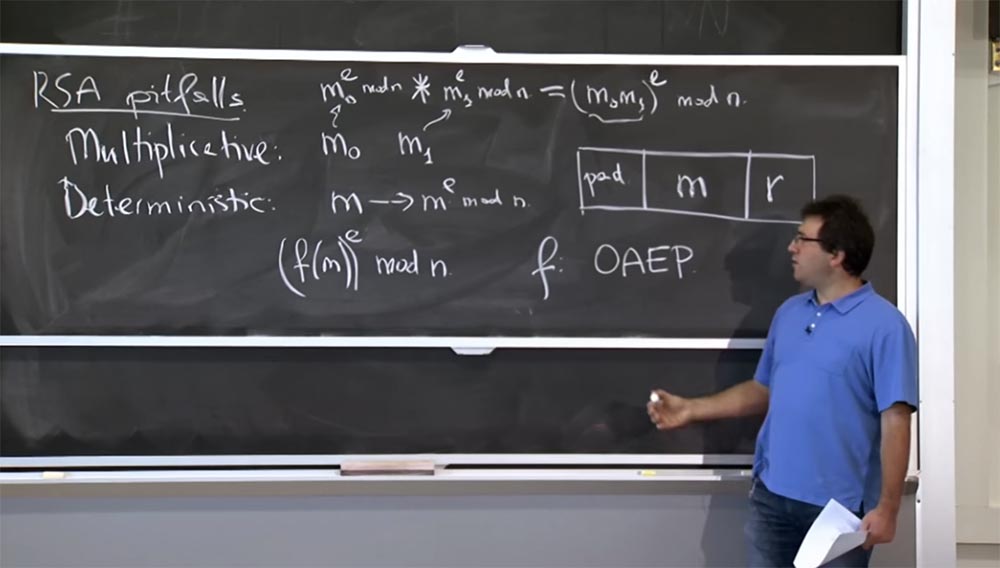Zielgruppe: Wenn ein Angreifer weiß, wie groß der Pad-Wert ist, kann er dann 1 ganz unten in der Sequenz setzen und diesen Wert dann multiplizieren?

Professor: Ja, vielleicht. Dies ist etwas kompliziert, da diese Zufälligkeit r weitergeht. Das spezifische Design dieses OAEP ist also etwas komplizierter als das, was ich dargestellt habe. Stellen Sie sich jedoch vor, dass dies eher eine Ganzzahl als eine bitweise Multiplikation ist. Die Zufälligkeit erstreckt sich weiter, sodass Sie ein OAEP-Schema erstellen können, in dem dies nicht der Fall ist.

Es stellt sich heraus, dass Sie diese RSA-Mathematik nicht direkt verwenden sollten. In der Praxis sollten Sie eine bestimmte Bibliothek verwenden, die all diese Dinge für Sie richtig implementiert, und sie als Verschlüsselungs- und Entschlüsselungsparameter verwenden.

Die oben diskutierten Details sind jedoch für uns von Wert, da wir tatsächlich versuchen, herauszufinden, wie die vorhandene RSA-Implementierung beschädigt oder angegriffen werden kann.

Insbesondere wird der im Vorlesungsartikel beschriebene Angriff die Tatsache ausnutzen, dass der Server dieses Pading-Add-On testen wird, wenn er die Nachricht empfängt. Auf diese Weise werden wir die Zeit berücksichtigen, die der Server zum Entschlüsseln benötigt. Wir werden eine sorgfältig erstellte Nachricht senden, die jedoch nicht aus der realen Nachricht m und ihrer Verschlüsselung erstellt wird. Wir werden einen gründlich verschlüsselten ganzzahligen Wert erstellen.

Der Server wird versuchen, es zu entschlüsseln, und es wird eine Art Absurdität auftreten, mit der das Pad-Pad höchstwahrscheinlich nicht gekoppelt wird, und der Server wird diese Nachricht sofort ablehnen. , , , , : RSA, , . , . , .

, , RSA. , , , . , , , 1000 . e .



, . , 1000 . 1000- , 1000 1000 n, . RSA , .
4 , . , . , CRT. . . , , , , [ = a ₁ ] mod p [ = a ₂ ] mod q, q – , .



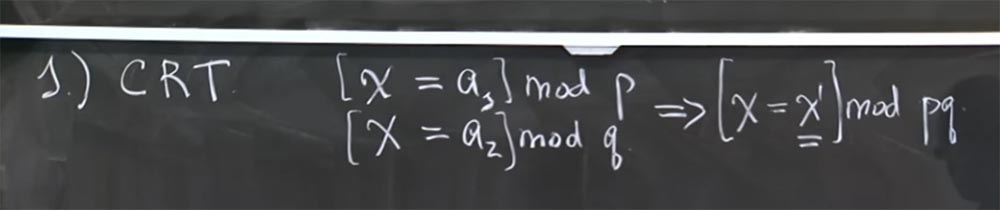
, [ = ¹ ] mod pq. ¹ , . ¹ , mod pq a ₁ a ₂ mod p q.

, ? , , n, p q.



, mod pq, mod p mod q. , , mod pq. , ? , , ?

: , ?

: , , , . , p q, n 1000 , p q 500 , . , , — , , . — . , , . 1000 512 , 2 . , 4 . [ = a ₁ ] mod p [ = a ₂ ] mod q , 4 . 2 RSA , .

, .

, Sliding windows, « ». . , .



, - , 500 , mod p mod q, d. c d? , c d . d , 500, . , , . , « ». .

c ^2x , : (c ^x ) ² :

c ^2x = (c ^x ) ²

c ^2x , 2 , cx, . , , c ^2x+1 :

c ^2x+1 = (c ^x ) ² x

.

, , , . , , , . , .

« », ? , . , , « » c ^2x+1 = (c ^x ) ² x .

, , , – , c ^2x+1 c ^2x , c. , , . , .



, :

1
3
7
...
31

. , , , .

, ^32x+y , 5 , 32- , ^y .



³² . , , , , c . «» .

29:00

MIT-Kurs "Computer Systems Security". 16: « », 2


.

Vielen Dank für Ihren Aufenthalt bei uns. Gefällt dir unser Artikel? Möchten Sie weitere interessante Materialien sehen? Unterstützen Sie uns, indem Sie eine Bestellung aufgeben oder Ihren Freunden empfehlen, einen Rabatt von 30% für Habr-Benutzer auf ein einzigartiges Analogon von Einstiegsservern, das wir für Sie erfunden haben: Die ganze Wahrheit über VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s von $ 20 oder wie teilt man den Server? (Optionen sind mit RAID1 und RAID10, bis zu 24 Kernen und bis zu 40 GB DDR4 verfügbar).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 mal günstiger? Nur wir haben 2 x Intel Dodeca-Core Xeon E5-2650v4 128 GB DDR4 6 x 480 GB SSD 1 Gbit / s 100 TV von 249 US-Dollar in den Niederlanden und den USA! Lesen Sie mehr über den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro für einen Cent?