MIT-Kurs "Computer Systems Security". Vorlesung 16: Angriffe durch den Seitenkanal, Teil 2

Massachusetts Institute of Technology. Vorlesung # 6.858. "Sicherheit von Computersystemen." Nikolai Zeldovich, James Mickens. 2014 Jahr

Computer Systems Security ist ein Kurs zur Entwicklung und Implementierung sicherer Computersysteme. Die Vorträge behandeln Bedrohungsmodelle, Angriffe, die die Sicherheit gefährden, und Sicherheitstechniken, die auf jüngsten wissenschaftlichen Arbeiten basieren. Zu den Themen gehören Betriebssystemsicherheit, Funktionen, Informationsflussmanagement, Sprachsicherheit, Netzwerkprotokolle, Hardwaresicherheit und Sicherheit von Webanwendungen.

Vorlesung 1: „Einführung: Bedrohungsmodelle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 2: „Kontrolle von Hackerangriffen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 3: „Pufferüberläufe: Exploits und Schutz“ Teil 1 / Teil 2 / Teil 3
Vorlesung 4: „Trennung von Privilegien“ Teil 1 / Teil 2 / Teil 3
Vorlesung 5: „Woher kommen Sicherheitssysteme?“ Teil 1 / Teil 2
Vorlesung 6: „Chancen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 7: „Native Client Sandbox“ Teil 1 / Teil 2 / Teil 3
Vorlesung 8: „Netzwerksicherheitsmodell“ Teil 1 / Teil 2 / Teil 3
Vorlesung 9: „Sicherheit von Webanwendungen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 10: „Symbolische Ausführung“ Teil 1 / Teil 2 / Teil 3
Vorlesung 11: „Ur / Web-Programmiersprache“ Teil 1 / Teil 2 / Teil 3
Vorlesung 12: Netzwerksicherheit Teil 1 / Teil 2 / Teil 3
Vorlesung 13: „Netzwerkprotokolle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 14: „SSL und HTTPS“ Teil 1 / Teil 2 / Teil 3
Vorlesung 15: „Medizinische Software“ Teil 1 / Teil 2 / Teil 3
Vorlesung 16: „Seitenkanalangriffe“ Teil 1 / Teil 2 / Teil 3

Zielgruppe: Wie werden zuerst x und y bestimmt?

Professor: Dazu müssen Sie den Aussteller in binärer Darstellung betrachten. Angenommen, ich versuche, den Wert von c ^1011010 zu berechnen, dann kann der Grad auch aus einer größeren Anzahl von Bits bestehen. Wenn wir ein erneutes Quadrieren durchführen möchten, müssen wir uns das niedrigste Bit ansehen - hier ist es 0.



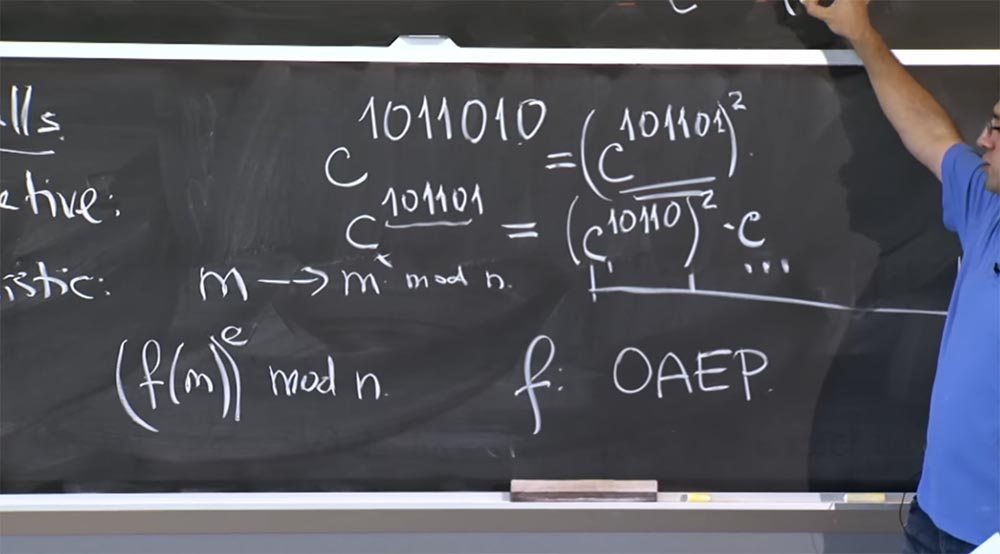
Somit erhalten wir die Gleichheit c ^1011010 = (c ¹⁰¹¹⁰¹ ) ²

Als nächstes müssen wir c ¹⁰¹¹⁰¹ berechnen, hier können wir diese Regel nicht verwenden, da sie nicht 2x ist - es wird x plus 1 sein. Deshalb schreiben wir diese Gleichheit:

c ¹⁰¹¹⁰¹ = (c ¹⁰¹¹⁰ ) ² c, da dieses Präfix 101101 = 10110 + 1 ist.

Daher multiplizieren wir das Quadrat mit c und verwenden es zum erneuten Quadrieren.

Für "Schiebefenster" müssen wir mehr Bits vom unteren Ende erfassen. Wenn Sie hier einen Trick mit einem „Schiebefenster“ machen möchten, anstatt eines von hier zu extrahieren, können wir unter Berücksichtigung dieser riesigen Tabelle 3 Bits gleichzeitig nehmen und an c7 festhalten. Wenn wir die ersten 3 Bits eines Grades nehmen, erhalten wir c ¹⁰¹¹⁰¹ = (c ¹⁰¹ ) ⁸ c ¹⁰¹ .

In diesem Fall haben wir wirklich die gleiche Anzahl von Berechnungen für (c ¹⁰¹ ) ⁸ , aber Sie können den Wert von c ¹⁰¹ in der Tabelle sehen. Und der Teil in Form von (c ¹⁰¹ ) ⁸ besagt, dass Sie "Schiebefenster" verwenden werden, um seinen Wert zu berechnen.



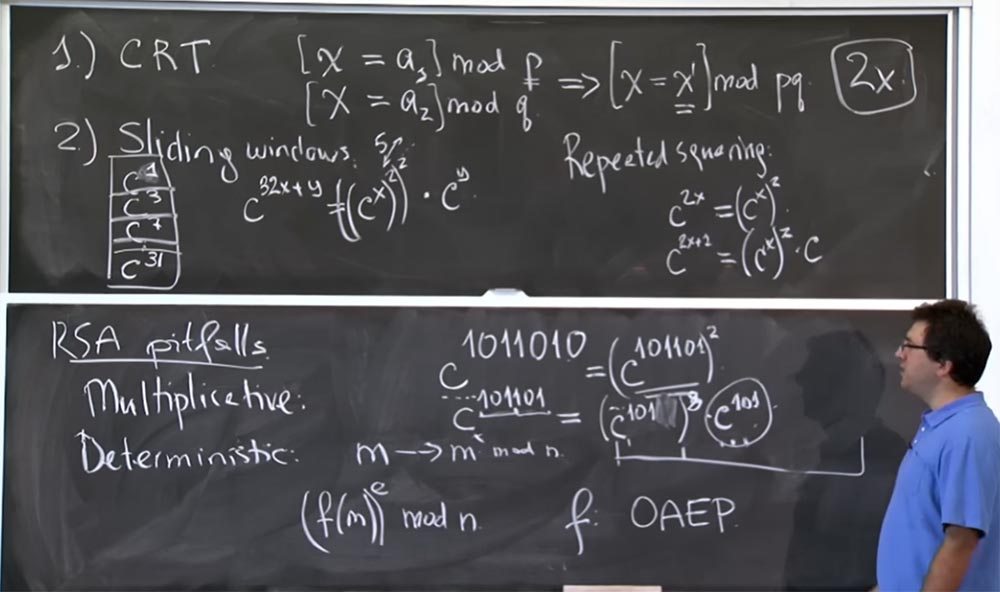
Dies spart viel Zeit, da vormultiplizierte Werte verwendet werden können. Vor 10 Jahren glaubte man, dass eine Wertetabelle bis zu 32 Grad der optimale Plan für die Recheneffizienz ist, weil es hier einen Kompromiss gibt, oder? Sie verbringen Zeit damit, diese Tabelle zu erstellen, sie sollte jedoch nicht zu groß sein, wenn Sie einige Datensätze nicht häufig verwenden. Angenommen, Sie erstellen eine Wertetabelle mit bis zu ⁵⁰⁰ Grad, verwenden jedoch keine Exponenten mit einem Wert größer als 128, und verschwenden nur Ihre Zeit.

Teilnehmerin: Gibt es einen Grund, einen solchen riesigen Tisch nicht im Voraus zu erstellen? Das heißt, die Werte einer begrenzten Anzahl von Graden zu berechnen, die bei den Berechnungen umgangen werden können?

Professor: Wenn Sie nicht im Voraus volumetrische Berechnungen durchführen möchten, gibt es zwei Dinge. Zum einen sollten Sie über einen Code verfügen, mit dem Sie überprüfen können, ob der erforderliche Datensatz in der Tabelle voll ist oder nicht. Dies verringert wahrscheinlich die Genauigkeit der Vorhersage der Zweige von CPU-Prozessen. Gleichzeitig arbeitet der Prozessor im allgemeinen Fall langsamer, da er prüfen muss, ob der erforderliche Datensatz in der Tabelle enthalten ist. Das zweite, was etwas ärgerlich ist, könnte das Durchsickern von Tabelleneinträgen durch verschiedene Seitenkanäle sein, nämlich durch Cache-Zugriffsmuster. Wenn also ein anderer Prozess auf demselben Prozessor ausgeführt wird, können Sie sehen, welche Cache-Adressen aus dem Cache entfernt oder verlangsamt werden, da jemand Zugriff auf Datensatz ³ oder Datensatz ^{31 hat} . Und je größer diese Tabelle wird, desto einfacher ist es zu bestimmen, welche Exponentenbits zum Erstellen des RSA-Schlüssels verwendet werden.

Diese riesige Tabelle kann erkennen, welche Cache-Adresse für den Prozessor verloren gegangen ist, dh, dass der Verschlüsselungsprozess Zugriff auf diesen Eintrag in der Tabelle haben sollte. Dies sagt Ihnen wiederum, dass die angegebene Folge von Bits im Exponenten Ihres privaten Schlüssels erscheint. Daher gehe ich davon aus, dass Sie diese Tabelle mathematisch so oft wie nötig ausfüllen können, aber in der Praxis möchten Sie nicht, dass sie eine gigantische Größe hat. Darüber hinaus können Sie große Tabelleneinträge nicht effektiv verwenden. Es ist viel nützlicher, die Datensätze einer relativ kleinen Tabelle wiederholt zu verwenden, um beispielsweise c ⁷ zu berechnen ^. Sie können den Wert c ³ zweimal verwenden und so weiter.

Hier ist also die RSA-Optimierung durch erneutes Quadrieren und "Schiebefenster" -Methoden. Ich weiß nicht, ob sie noch diese Größe von "Schiebefenstern" verwenden, aber auf jeden Fall beschleunigt dies den Berechnungsprozess, da Sie sonst jedes Bit des Exponenten quadrieren und dann mit jedem Bit multiplizieren müssten. Wenn Sie also einen 500-Bit-Exponenten haben, müssten Sie 500 Quadrate und ungefähr 256 Multiplikationen mit c vervollständigen. Bei „Schiebefenstern“ müssen Sie noch 512 Quadrate erstellen, da dies nicht vermieden werden kann. Die Anzahl der Multiplikationen mit c verringert sich jedoch aufgrund der Verwendung von Einträgen aus der Tabelle von 256 auf etwa 32.

Dies ist der allgemeine Optimierungsplan, der den Berechnungsprozess um das Eineinhalbfache beschleunigt. Dies ist eine ziemlich einfache Optimierung. Es gibt zwei clevere Tricks mit Zahlen, die den Multiplikationsprozess effizienter machen.

Die erste ist die Montgomery-Transformation, in einer zweiten werden wir sehen, warum dies für uns besonders wichtig ist. Diese Optimierung versucht, ein Problem für uns zu lösen: Jedes Mal, wenn wir die Multiplikation durchführen, erhalten wir eine Zahl, die weiter wächst und in aufsteigender Reihenfolge wächst. Insbesondere haben Sie sowohl in „Schiebefenstern“ als auch beim erneuten Quadrieren tatsächlich 2 Zahlen miteinander multipliziert, als Sie c auf die Potenz von y angehoben haben.

Das Problem ist, dass, wenn die Eingabedaten c ^x und c ^y für die Multiplikation beispielsweise jeweils 512 Bit wären, die Größe des Multiplikationsergebnisses 1000 Bit betragen würde. Danach nehmen Sie dieses 1000-Bit-Ergebnis und multiplizieren es erneut mit etwa 512 Bit. Es hat die Größe von 1500, 2000, 2500 Bit und alles wächst und wächst.

Sie möchten dies jedoch nicht, da die Multiplikation die Reihenfolge der multiplizierten Zahlen erhöht. Aus diesem Grund müssen wir unsere Zahlengröße so klein wie möglich halten, im Grunde genommen gleich 512 Bit, da alle diese Berechnungen mod p oder mod q sind.

Wir können diese Zahl reduzieren, indem wir beispielsweise (((c ^x ) ² ) ² ) ² berechnen. Sie können beispielsweise cx modulo p berechnen, dann erneut modulo p und erneut modulo p quadrieren. Diese Methode ist relativ gut, da wir so die Größe unserer Zahl innerhalb von 512 Bit halten können, dh so klein wie möglich. Dies ist gut, um die Größe der Zahlen zu reduzieren, die wir multiplizieren müssen, aber tatsächlich erhöht die Operation mit diesem Modul p die Kosten der Berechnung erheblich.



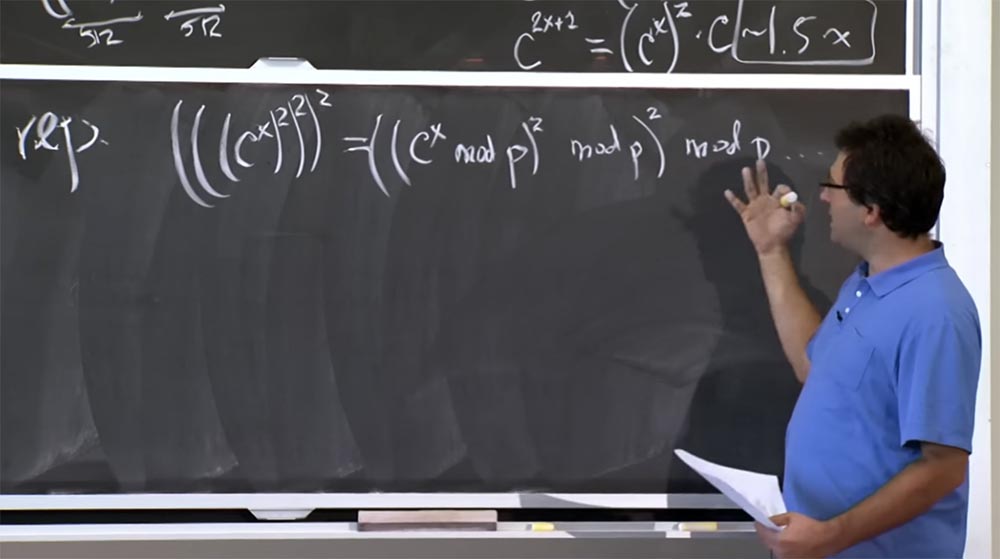
Weil die Art und Weise, wie du mod p bekommst, in Teilung ist. Und Division ist schlimmer als Multiplikation. Ich werde die Algorithmen für die Division nicht auflisten, aber es ist sehr langsam. Normalerweise versuchen Sie, Divisionsoperationen nach Möglichkeit zu vermeiden, da dies keine einfache Programmierung ist. Tatsache ist, dass Sie eine Art von Approximationsalgorithmen, Newtons Methoden und dergleichen verwenden müssen, und all dies verlangsamt den Berechnungsprozess.

Die Multiplikation ist viel rentabler, aber die Verwendung von Mod p- oder Mod q-Operationen zur Reduzierung der Zahlengröße kostet mehr als die Multiplikation. Ich werde Ihnen einen Weg zeigen, dies zu vermeiden und wie Sie mit der Montgomery-Transformation schnelle Berechnungen durchführen können.

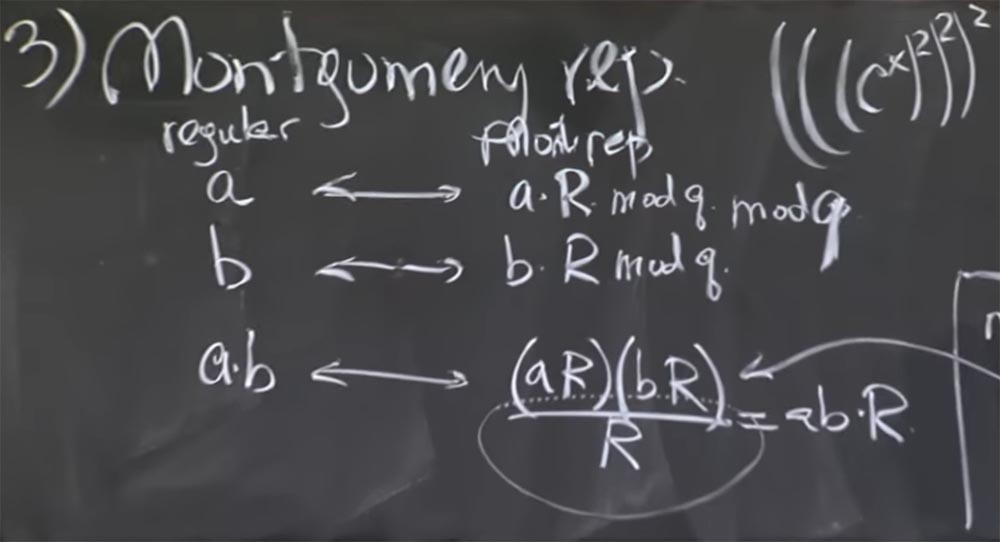
Die Grundidee besteht darin, die Ganzzahlen, die Sie multiplizieren möchten, in Form einer Montgomery-Transformation darzustellen. Das ist eigentlich sehr einfach. Dazu multiplizieren wir einfach unsere Zahl a mit einem bestimmten magischen Wert R. Nach einer Sekunde werde ich Ihnen sagen, was es ist. Aber lassen Sie uns zuerst herausfinden, was passiert, wenn wir einen beliebigen Wert von R auswählen.

Wir nehmen also zwei Zahlen, a und b, und konvertieren sie in die Montgomery-Darstellung, wobei wir jede mit R multiplizieren. Dann sieht das Produkt von a und b in der Montgomery-Transformation folgendermaßen aus:

ab <-> (aR) (bR) / R = abR

Das heißt, Sie multiplizieren aR mit bR und erhalten das Produkt von ab mit R im Quadrat. Jetzt haben wir zwei Rs, das ist etwas ärgerlich, aber Sie können es durch R teilen. Als Ergebnis erhalten wir das Produkt von ab durch R. Es ist ein bisschen unklar, warum wir diese Zahl noch einmal multiplizieren mussten. Lassen Sie uns zuerst herausfinden, ob dies richtig ist, und dann werden wir verstehen, warum es schneller sein wird.
Dies ist insofern richtig, als es sehr einfach ist. Wenn Sie einige Zahlen multiplizieren möchten, müssen Sie sie mit diesem Wert von R multiplizieren und die Montgomery-Transformation erhalten. Jedes Mal, wenn wir diese beiden Zahlen multiplizieren, müssen wir sie durch R dividieren und dann die resultierende Form der Transformation der Form abR betrachten. Wenn wir dann mit dem Quadrieren, Multiplizieren und all diesen Dingen fertig sind, kehren wir zur normalen, gewöhnlichen Form des Ergebnisses zurück und dividieren einfach zum letzten Mal durch R.



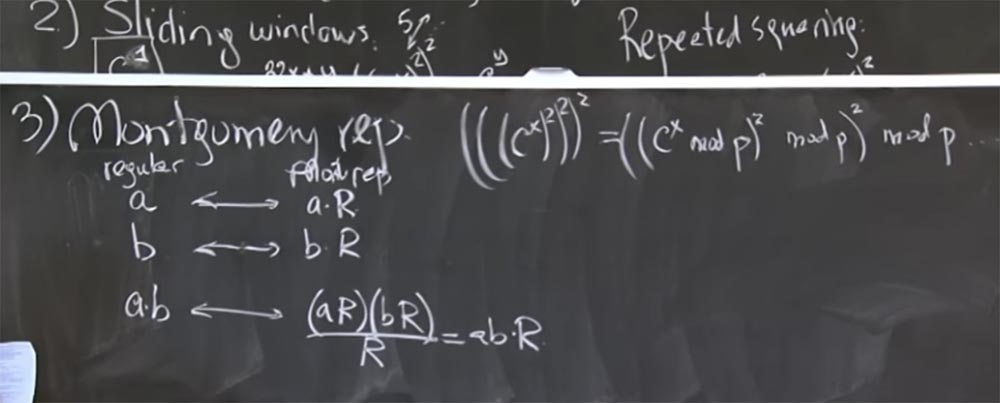
Überlegen Sie nun, wie Sie die am besten geeignete Zahl für R auswählen, um das Teilen durch R zu einer sehr schnellen Operation zu machen. Und das Coolste hier ist, dass wenn die Division durch R sehr schnell ist, wenn es eine kleine Zahl ist, und wir diesen Mod q nicht zu oft machen müssen. Insbesondere wird aR, sagen wir, auch eine Größe von ungefähr 500 Bit haben, weil all dies tatsächlich mod p oder mod q ist. Somit beträgt aR 500 Bit, bR beträgt ebenfalls 500 Bit, so dass das Produkt (aR) (bR) 1000 Bit beträgt. R wird auch eine bequeme 500-Bit-Zahl sein, die Größe von p. Und wenn wir die Divisionsoperation schnell genug machen können, dann ist das Ergebnis von ab auch ungefähr eine 500-Bit-Zahl, so dass wir ohne zusätzliche Division multiplizieren können. Das Teilen durch R ist viel rentabler und liefert ein kleines Ergebnis, wodurch die Verwendung von mod p in den meisten Situationen vermieden wird.

Also, was ist diese seltsame R-Nummer, über die ich die ganze Zeit spreche? Es hat einen Wert von 2 bis 512 Grad:

R = 2 ⁵¹²

Es wird 1 und eine Reihe von Nullen sein, daher ist es einfach, mit einer solchen Zahl zu multiplizieren, da es ausreicht, nur eine Reihe von Nullen zum Ergebnis hinzuzufügen. Die Division kann auch einfach sein, wenn die niedrigstwertigen Bits des Ergebnisses Null sind. Wenn Sie also einen Wert aus einem Haufen von Bits haben, der von 512 Nullen begleitet wird, ist das Teilen durch 2 bis 512 Grad sehr einfach - Sie lassen einfach Nullen auf der rechten Seite fallen, und dies ist eine völlig korrekte Teilungsoperation.

Das kleine Problem ist, dass wir bei dieser Multiplikation tatsächlich keine Nullen auf der rechten Seite haben. Wir haben echte 512-Bit-Zahlen, die alle 512-Bit verwenden.

Das Produkt von (aR) durch (bR) ist auch eine reelle Zahl in der Größenordnung von 1000 Bits, so dass wir nicht einfach die niedrigstwertigen Bits fallen lassen können. Ein vernünftiger Ansatz basiert jedoch auf der Tatsache, dass das einzige, was uns Sorgen macht, der Wert von mod p ist. Somit können Sie diesem Wert immer mehrere p hinzufügen, ohne das Mod p-Äquivalent zu ändern. Infolgedessen können wir ein Vielfaches von p-Werten hinzufügen, so dass alle niedrigstwertigen Bits zu Nullen werden. Schauen wir uns einige einfache Beispiele an. Ich werde keine 512 Bits an die Tafel schreiben, aber ich werde nur ein kurzes Beispiel geben.

Angenommen, in unserer Situation ist R = 2 ⁴ = 10000. Dies ist eine viel kleinere Größe als sie tatsächlich ist. Mal sehen, wie diese Montgomery-Transformation funktioniert. Wir versuchen mod q zu berechnen, wobei q = 7 ist. In binärer Form ist q = 7 (111).

Angenommen, wir haben eine Multiplikation (aR) (bR) durchgeführt, und in der binären Darstellung ist das Ergebnis 11010, dh dies ist der Wert des Produkts (aR) (bR). Wie teilen wir es durch R?

Offensichtlich sind nicht alle vier niedrigstwertigen Bits Nullen, daher können wir sie nicht einfach trennen, sondern auch Mengen hinzufügen, die ein Vielfaches von q sind. Insbesondere können wir 2 mal in q addieren, wobei 2q = 1110 in binärer Darstellung ist. Als Ergebnis bekommen wir 101000, ich hoffe ich habe alles richtig gemacht.



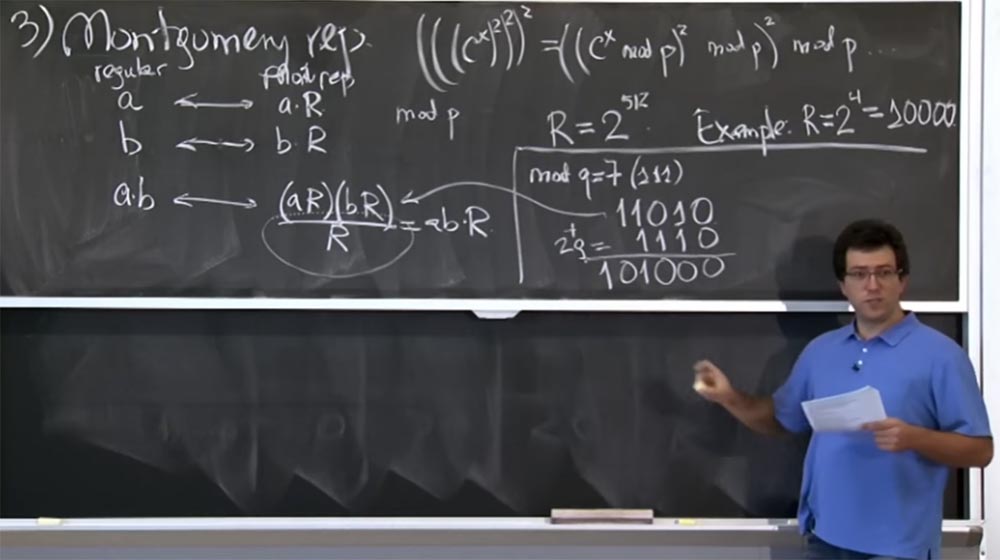
Wir haben also die Summe (aR) (bR) + 2q. Tatsächlich interessiert uns + 2q nicht, denn alles, was uns interessiert, ist der Wert von mod q. Jetzt sind wir näher am Ziel, weil wir rechts drei Nullen haben. Jetzt können wir noch etwas q hinzufügen. Nehmen wir an, diesmal ist es 8q, also 111000. Fügen Sie erneut unsere Zeilen hinzu und erhalten Sie 1100000. Jetzt haben wir das Original (aR) (bR) + 2q + 8q = 1100000. Schließlich können wir dieses Ding sehr leicht in unterteilen R, nur vier niedrige Nullen fallen lassen.



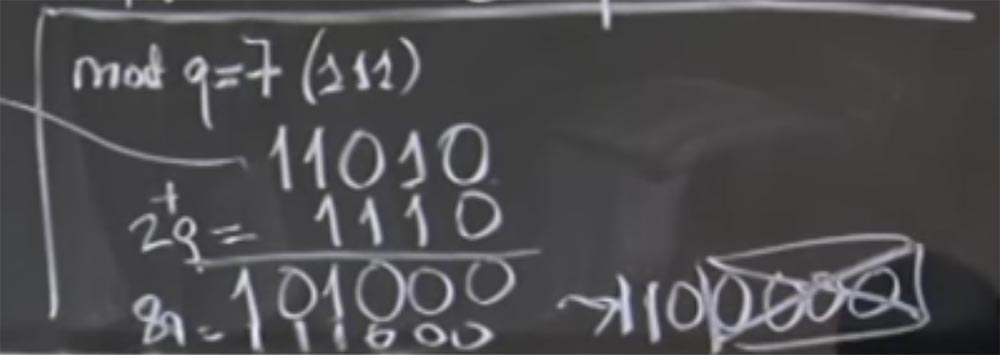Zielgruppe: Produkt (aR) (bR) endet immer mit 1024 Nullen?

Professor: Nein, und ich werde erklären, was die Verwirrung sein könnte. Nehmen wir an, die Zahl a ist 512 Bit, wir haben sie mit R multipliziert und eine 1000-Bit-Zahl erhalten. In diesem Fall haben Sie Recht, aR ist die Zahl, in der die hohen Bits a und die niedrigen Bits alle Nullen sind. Aber dann führen wir mod q aus, um es kleiner zu machen. Daher ist die Größe von 1024 Bits im allgemeinen Fall ein Unfall, da diese Zahl diese niedrigen Nullen nur während der ersten Konvertierung aufweist, aber nachdem Sie einige Multiplikationen durchgeführt haben, handelt es sich um beliebige Bits.

Um Sie nicht irrezuführen, musste ich hier nach aR und nach bR mod q schreiben - hier füge ich es hinzu - und diesen mod q berechnen, sobald Sie die Konvertierung durchführen, um den Wert zu reduzieren.



Die anfängliche Umwandlung ist ziemlich mühsam oder mindestens so kostspielig wie die herkömmliche Modulation bei der Multiplikation. Das Coole ist, dass Sie diesen Preis einmal bezahlen, wenn Sie die Montgomery-Konvertierung durchführen, und ihn dann nicht in jedem Schritt der Berechnungen zurückkonvertieren, sondern nur in Form einer Montgomery-Ansicht beibehalten.
Denken Sie daran, dass Sie mehr als 500 Multiplikationen durchführen müssen, um eine Potenz mit 512 Bit zu erreichen, da wir mindestens 500 Quadrate und einige weitere ausführen müssen. Sie modifizieren also zweimal q und erhalten dann viele einfache Divisionsoperationen, wenn Sie in dieser Form der Darstellung von Zahlen bleiben. Und am Ende machen Sie eine Division durch R, um zu dieser Form ab zurückzukehren.

Anstatt mod q 500 Mal für jeden Schritt der Multiplikation auszuführen, führen Sie mod q zweimal aus und führen diese Unterteilungen durch R dann mit minimalen Kosten fort.
Teilnehmerin: Wenn Sie ein Vielfaches von q addieren und dann durch R dividieren, haben wir dann einen Rest?
Professor: eigentlich bedeutet mod q den Rest, wenn Sie durch q teilen. Einfach ausgedrückt, x + yq mod q = x. In diesem Fall gibt es eine weitere nützliche Eigenschaft: Alle Module sind Primzahlen. Dies gilt ebenso wie die Tatsache, dass wenn Sie (x + yq / R) mod q haben, es gleich x / R mod q ist.



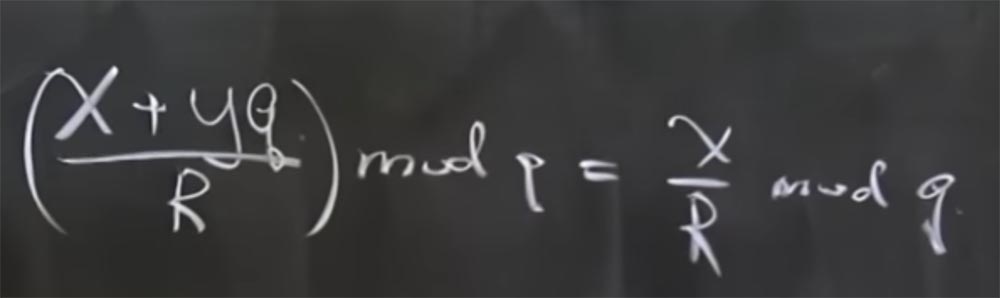
Der Grund dafür ist, dass es in der modularen Arithmetik keine echten Divisionsoperationen gibt, sondern nur eine Inversion. Tatsächlich bedeutet dies, dass wenn wir (x + yq) mit invertiertem R multipliziert mit mod q multipliziert haben, es gleich der Summe zweier Produkte ist: das Produkt x des invertierten R mit mod q und das Produkt von yq mit dem invertierten R mit mod q. Außerdem wird der letzte Term reduziert, weil er mit q multipliziert wird.



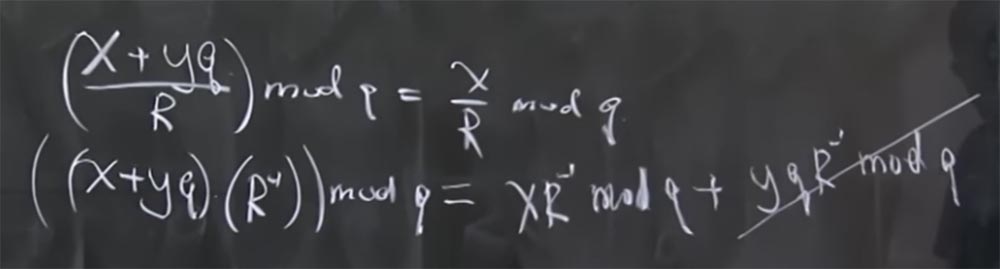
Für Dinge wie das Summieren von 2q, 8q usw. gibt es eine Formel, die den Berechnungsprozess beschleunigt. Ich habe es schrittweise gemacht, zuerst 2q berechnet, dann 8q und so weiter, aber die Vorlesungsmaterialien haben eine vollständige Formel, die verwendet werden kann. Ich möchte einfach keine Zeit damit verschwenden, sie an die Tafel zu schreiben. Sie können berechnen, welches Vielfache des q-Werts Sie addieren müssen, damit alle niedrigstwertigen Bits zu 0 werden. Um die Division durch R durchzuführen, müssen Sie nur dieses magische Vielfache von q berechnen, addieren und dann das Tief verwerfen Null Bits, und dies gibt Ihre Zahl auf 512 Bits zurück, unabhängig von der Größe des Ergebnisses, das Sie erhalten.

Aber es gibt eine Subtilität. Der einzige Grund, warum wir darüber sprechen, ist, dass hier etwas Lustiges passiert, das es uns ermöglicht, Informationen über die Timings herauszufinden. Insbesondere, obwohl wir durch R geteilt haben, wissen wir immer noch, dass das Ergebnis ungefähr 512 Bit sein wird. Aber es kann immer noch mehr als q sein, da q keine 512-Bit-Zahl ist, kann es etwas kleiner als R sein.

Es kann also sein, dass wir nach dieser vorteilhaften Division durch R q erneut subtrahieren müssen, weil wir etwas Kleines erhalten, das aber immer noch nicht klein genug ist. Es besteht also die Möglichkeit, dass wir nach dieser Division q erneut subtrahieren müssen. Und diese Subtraktion kann als Teil des Angriffs verwendet werden, da die Subtraktionsoperation die Berechnungszeit addiert.



Und jemand hat herausgefunden - nicht diese Leute, sondern jemand in der vorherigen Arbeit -, dass es eine Chance gibt, etwas zu tun, das als zusätzliche Reduzierung oder zusätzliche Reduzierung bezeichnet wird. , . , xd mod q, - x mod q, 2R. .



, x mod q , . , cd.



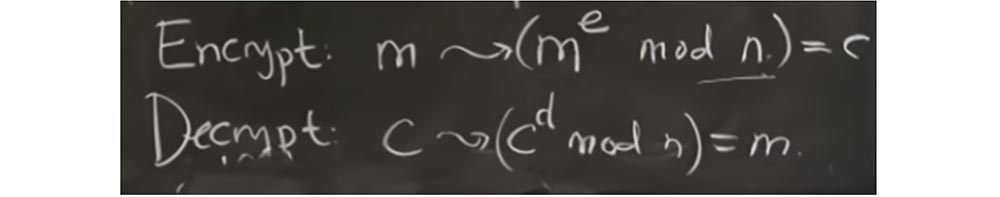
, extra reduction , X , , , q.



, c, extra reduction , c — q. , , q . , extra reduction, , , X mod q , = q + έ, . , . , , , , extra reduction .

: , ?

: , extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .

, . , - , . — , . , - , extra reduction .

, . , OpenSSL, , . , mod q . , , .

, , , , a b. — 512- . , 32- , , 64- ? ?



- ? , , a b .

, , 512 , 64- , 32- . a : a ₁ a ₀ , a ₀ , a ₁ — . b – b ₁ b ₀ .

ab 3- : a ₁ b ₁ , a ₀ b ₀ , a ₁ b ₀ + a ₀ b ₁ . .



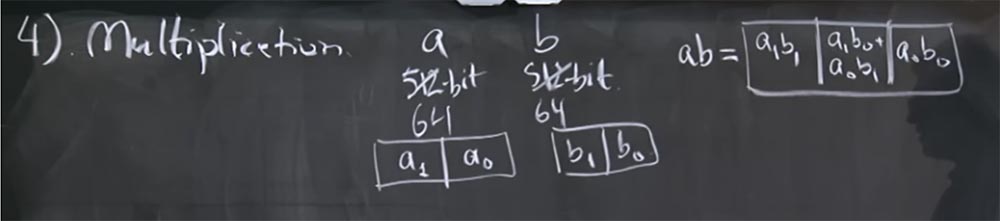
55:00

MIT-Kurs "Computer Systems Security". 16: « », 3


.

Vielen Dank für Ihren Aufenthalt bei uns. Gefällt dir unser Artikel? Möchten Sie weitere interessante Materialien sehen? Unterstützen Sie uns, indem Sie eine Bestellung aufgeben oder Ihren Freunden empfehlen, einen Rabatt von 30% für Habr-Benutzer auf ein einzigartiges Analogon von Einstiegsservern, das wir für Sie erfunden haben: Die ganze Wahrheit über VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s von $ 20 oder wie teilt man den Server? (Optionen sind mit RAID1 und RAID10, bis zu 24 Kernen und bis zu 40 GB DDR4 verfügbar).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 mal günstiger? Nur wir haben 2 x Intel Dodeca-Core Xeon E5-2650v4 128 GB DDR4 6 x 480 GB SSD 1 Gbit / s 100 TV von 249 US-Dollar in den Niederlanden und den USA! Lesen Sie mehr über den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro für einen Cent?