MIT-Kurs "Computer Systems Security". Vorlesung 16: „Seitenkanalangriffe“, Teil 3

Massachusetts Institute of Technology. Vorlesung # 6.858. "Sicherheit von Computersystemen." Nikolai Zeldovich, James Mickens. 2014 Jahr

Computer Systems Security ist ein Kurs zur Entwicklung und Implementierung sicherer Computersysteme. Die Vorträge behandeln Bedrohungsmodelle, Angriffe, die die Sicherheit gefährden, und Sicherheitstechniken, die auf jüngsten wissenschaftlichen Arbeiten basieren. Zu den Themen gehören Betriebssystemsicherheit, Funktionen, Informationsflussmanagement, Sprachsicherheit, Netzwerkprotokolle, Hardwaresicherheit und Sicherheit von Webanwendungen.

Vorlesung 1: „Einführung: Bedrohungsmodelle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 2: „Kontrolle von Hackerangriffen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 3: „Pufferüberläufe: Exploits und Schutz“ Teil 1 / Teil 2 / Teil 3
Vorlesung 4: „Trennung von Privilegien“ Teil 1 / Teil 2 / Teil 3
Vorlesung 5: „Woher kommen Sicherheitssysteme?“ Teil 1 / Teil 2
Vorlesung 6: „Chancen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 7: „Native Client Sandbox“ Teil 1 / Teil 2 / Teil 3
Vorlesung 8: „Netzwerksicherheitsmodell“ Teil 1 / Teil 2 / Teil 3
Vorlesung 9: „Sicherheit von Webanwendungen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 10: „Symbolische Ausführung“ Teil 1 / Teil 2 / Teil 3
Vorlesung 11: „Ur / Web-Programmiersprache“ Teil 1 / Teil 2 / Teil 3
Vorlesung 12: Netzwerksicherheit Teil 1 / Teil 2 / Teil 3
Vorlesung 13: „Netzwerkprotokolle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 14: „SSL und HTTPS“ Teil 1 / Teil 2 / Teil 3
Vorlesung 15: „Medizinische Software“ Teil 1 / Teil 2 / Teil 3
Vorlesung 16: „Seitenkanalangriffe“ Teil 1 / Teil 2 / Teil 3

Teilnehmerin: Verwenden Sie die Karatsuba-Methode?

Professor: Ja, dies ist eine intelligente Multiplikationsmethode, für die keine vier Berechnungsstufen erforderlich sind. Die Karatsuba-Methode wird im .601-Kurs unterrichtet, oder wie wird sie heute bezeichnet?

Teilnehmerin: 042.

Professor: 042, ausgezeichnet. Ja, das ist eine sehr gute Methode. Fast jede kryptografische Bibliothek verwendet es. Für diejenigen unter Ihnen, die keine Absolventen unseres Instituts sind - ich sage dies, weil wir hier Doktoranden haben - werde ich an die Tafel über die Karatsuba-Methode schreiben. Hier müssen Sie drei Werte berechnen:

a ₁ b ₁
(a ₁ - a ₀ ) (b ₁ - b ₀ )
a ₀ b ₀

Sie führen also drei statt vier Multiplikationen durch, und es stellt sich heraus, dass Sie diesen Wert a ₁ b ₀ + a ₀ b ₁ aus diesen drei Multiplikationsergebnissen wiederherstellen können.



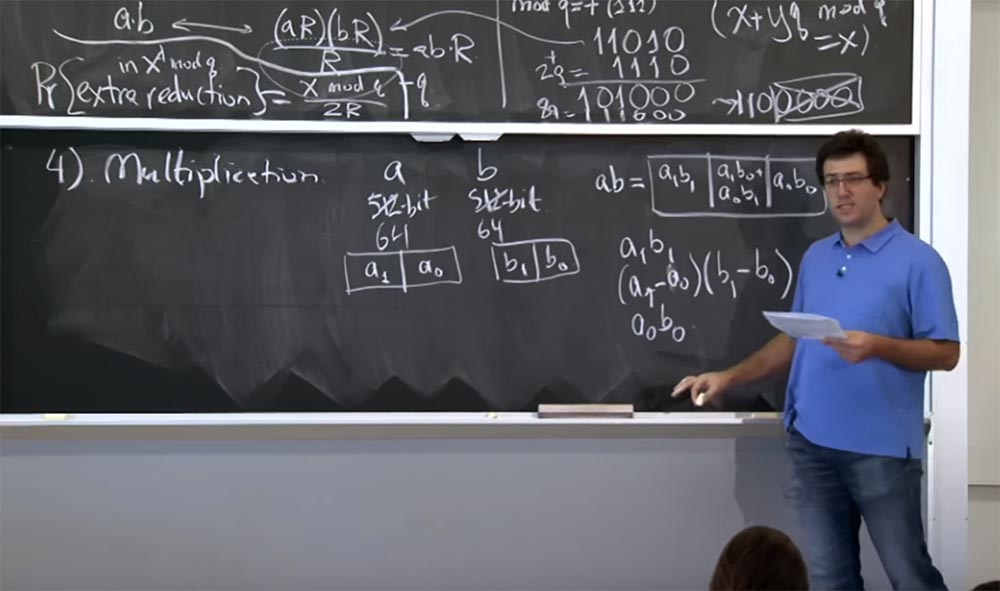
Der besondere Weg, dies zu tun, ist dies ... lassen Sie es mich in eine andere Form bringen.

Also werden wir haben:

(2 ⁶⁴ + 2 ³² ) (a ₁ b ₁ ) +
(2 ³² ) (- (a ₁ - a ₀ ) (b ₁ - b ₀ )
(2 ³² + 1) (a ₀ b ₀ )

Dies ist nicht sehr klar, aber wenn Sie die Details herausarbeiten, dann überzeugen Sie sich letztendlich davon, dass dieser Wert in diesen 3 Zeilen äquivalent zu ab ist, reduziert aber gleichzeitig die Berechnung um eine Multiplikation. Und die Art und Weise, wie wir dies auf voluminösere Multiplikationen anwenden, ist, dass Sie rekursiv weiter nach unten gehen. Wenn Sie also 512-Bit-Werte haben, können Sie diese in 256-Bit-Multiplikation aufteilen. Sie führen drei 256-Bit-Multiplikationen durch, jedes Mal rekursiv mit der Karatsuba-Methode. Am Ende kommen Ihre Berechnungen auf die Maschinengröße und können von einer einzelnen Maschinenanweisung verarbeitet werden.



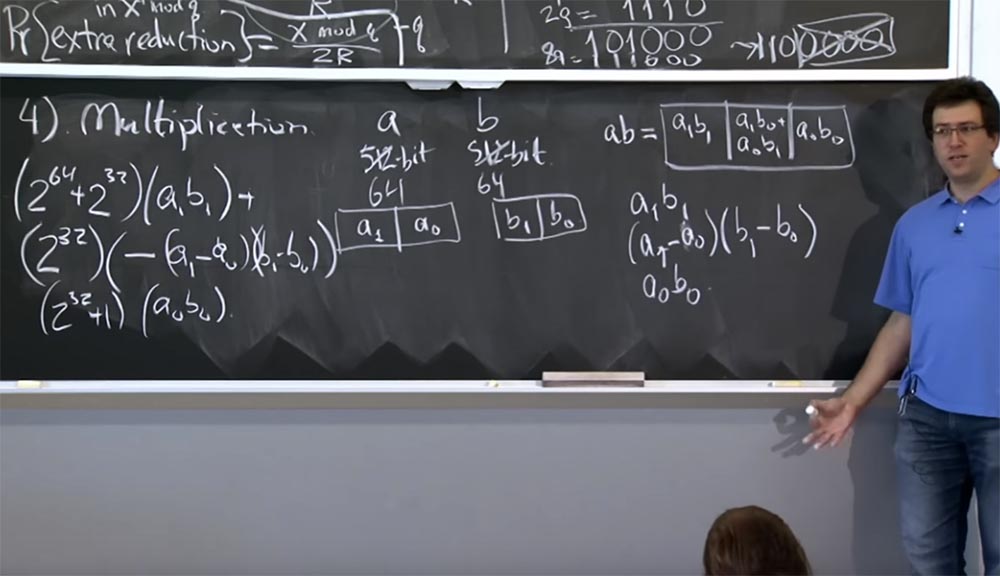
Wo ist also der Timing-Angriff? Wie verwenden diese Leute die Karatsuba-Multiplikation? Es stellt sich heraus, dass OpenSSL sich Sorgen über zwei Arten der Multiplikation macht, die Sie möglicherweise durchführen müssen.
Die erste ist die Multiplikation von zwei großen Zahlen von ungefähr derselben Größe. Dies passiert oft, wenn wir eine modulare Exponentiation durchführen, da alle Werte, die wir multiplizieren, eine Größe von ungefähr 512 Bit haben. Wenn wir also c mit y oder Quadrat multiplizieren, multiplizieren wir zwei Dinge von ungefähr derselben Größe. In diesem Fall ist die Karatsuba-Methode sehr sinnvoll, da sie die Größe der quadratischen Zahlen um das 1,58-fache reduziert, was den Berechnungsprozess erheblich beschleunigt.
Die zweite Art der Multiplikation ist, wenn OpenSSL zwei Zahlen multipliziert, deren Größe sich erheblich voneinander unterscheidet: eine ist sehr groß und die andere ist sehr klein. In diesem Fall können Sie auch die Karatsuba-Methode verwenden, diese funktioniert jedoch langsamer als die primitive Multiplikation. Angenommen, Sie multiplizieren eine 512-Bit-Zahl mit einer 64-Bit-Zahl. Sie müssen jedes Bit der ersten Zahl auf eine Potenz von 64 erhöhen, was zu einer Verlangsamung des Prozesses um 2n anstelle einer Beschleunigung von n / 1,58 führt. Daher haben diese Leute, die OpenSSL verwenden, versucht, klüger zu werden, und hier begannen die Probleme.

Sie beschlossen, dynamisch zwischen der effektiven Karatsuba-Methode und der Multiplikationsmethode der Grundschule zu wechseln. Ihre Heuristik war wie folgt. Wenn die beiden Zahlen, die Sie multiplizieren, aus der gleichen Anzahl von Maschinenwörtern bestehen oder mindestens die gleiche Anzahl von Bits wie 32-Bit-Einheiten haben, wird die Karatsuba-Methode verwendet. Wenn sich zwei Zahlen in ihrer Größe stark voneinander unterscheiden, wird eine normale Multiplikation durchgeführt.

In diesem Fall können Sie verfolgen, wie der Wechsel zu einer anderen Multiplikationsmethode erfolgt. Da der Moment des Umschaltens nicht spurlos vergeht, wird sich danach bemerkbar machen, ob er jetzt viel mehr Zeit für die Multiplikation benötigt oder viel weniger als zuvor. Die Forscher nutzten diesen Umstand, um einen Angriff mithilfe der Timing-Methode zu organisieren.

Ich glaube, ich habe Ihnen alle seltsamen Tricks erzählt, die die Leute bei der Implementierung von RSA in der Praxis anwenden. Versuchen wir nun, sie zusammenzusetzen und in Bezug auf den gesamten Webserver zu verwenden, um herauszufinden, wie Sie die für uns interessanten Teile aus dem Eingangsnetzwerkpaket "abklemmen" können.

Wenn Sie sich an die Vorlesung über HTTPS erinnern, verfügt der Webserver über einen geheimen Schlüssel. Er verwendet diesen geheimen Schlüssel, um zu beweisen, dass er der richtige Eigentümer aller Zertifikate über HTTPS oder TLS ist. Dies liegt an der Tatsache, dass Clients einige zufällig ausgewählte Bits senden, diese Bits mit dem öffentlichen Schlüssel des Servers verschlüsselt werden und der Server diese Nachricht mithilfe des TLS-Protokolls entschlüsselt. Und wenn die Nachricht überprüft wird, werden diese zufälligen Bits verwendet, um eine Kommunikationssitzung einzurichten.

In unserem Fall wird diese Nachricht jedoch nicht überprüft, da sie auf besondere Weise erstellt wird. Wenn sich herausstellt, dass die zusätzlichen Bits nicht übereinstimmen, gibt der Server einen Fehler zurück, sobald die Entschlüsselung unserer Nachricht abgeschlossen ist.

Folgendes werden wir hier tun. Der Server - Sie können davon ausgehen, dass es sich um Apache mit offenem SSL handelt - erhält vom Client eine Nachricht, die er als verschlüsselten Text mit oder als hypothetischen verschlüsselten Text betrachtet, den der Client erstellt hat. Das erste, was wir mit dem Chiffretext c machen, ist, ihn mit der Formel mit → (c ^d mod n) = m zu entschlüsseln.

Wenn Sie sich an die erste Optimierung erinnern, wenden wir den chinesischen Restsatz an und teilen unseren Text in zwei Teile: einen, der nach mod p berechnet wird, den anderen nach mod q, und kombinieren dann die Ergebnisse. Nehmen Sie zuerst c und stellen Sie es in zwei Größen dar: Die erste heißt c ₀ , ist gleich mod q und die zweite ist c ₁ und ist gleich c mod p. Dann werden wir dasselbe tun, um c für d mod p und c für d mod q zu berechnen.



Als nächstes wechseln wir zur Montgomery-Ansicht, da dies unsere Multiplikationen sehr schnell macht. Das nächste, was SSL mit Ihrer Nummer machen wird, ist, c ₀ 'zu berechnen, was gleich c ₀ R mod q ist, und hier unten dasselbe für c1 zu tun. Ich werde es nicht aufschreiben, weil es gleich aussieht .

Nachdem wir zur Montgomery-Form gewechselt sind, können wir endlich unsere Multiplikationen durchführen, und hier werden wir die "Schiebefenster" -Technik verwenden. Sobald wir c ₀ 'erhalten, machen wir diese einfache Erhöhung von c ₀ ' auf die Potenz von d in mod q. Und hier, da wir diesen Wert für d berechnen, werden wir "Schiebefenster" für Bits des Exponenten d verwenden, und wir werden auch die Karatsuba-Methode oder die übliche Multiplikation verwenden, abhängig von der Größe unserer Operanden.



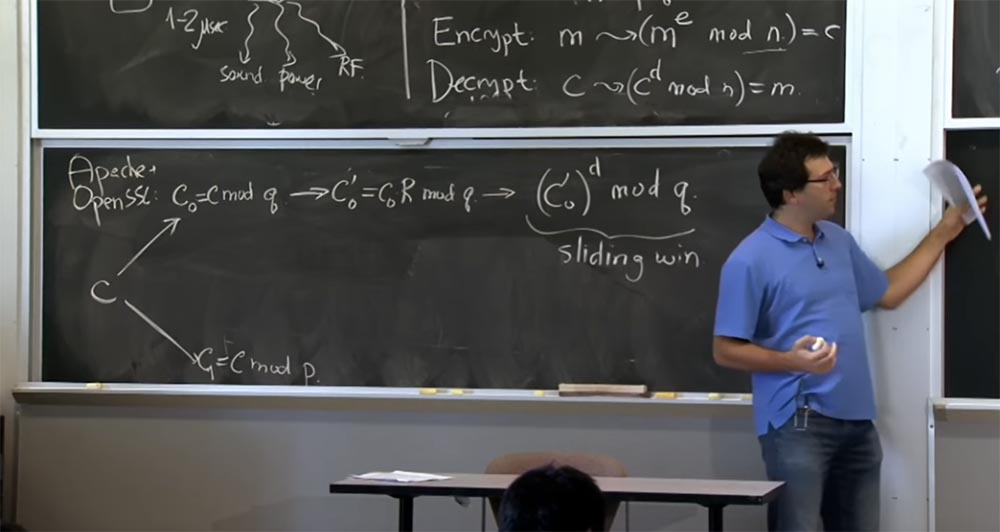
Wenn sich also herausstellt, dass dieser Wert c ₀ 'und das zuvor erhaltene Quadrierungsergebnis dieselbe Größe haben, verwenden wir die Karatsuba-Methode. Wenn c ₀ 'sehr klein ist und das vorherige Ergebnis der Multiplikation groß ist, werden wir auf die übliche Weise quadrieren und multiplizieren. Hier verwenden wir "Schiebefenster" und die Karatsuba-Methode anstelle der normalen Multiplikation.



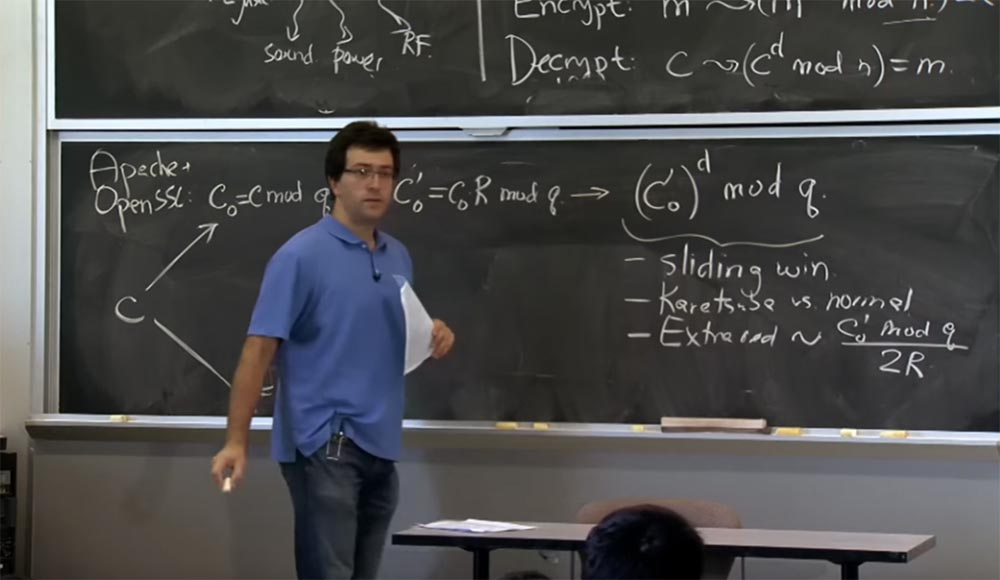
Auch in dieser Phase treten zusätzliche Reduzierungen auf. Weil mit jeder Multiplikation zusätzliche Reduktionen proportional zu dem sind, was wir zur Potenz von mod q erhöhen, dh zum Wert von (c ₀ ') ^d . Hier ist bei einer einfachen Verbindung der Formel die Wahrscheinlichkeit zusätzlicher Reduktionen proportional zum Wert c ₀ 'mod q geteilt durch 2R. An dieser Stelle erscheint ein Bit, das das Timing beeinflusst.

Tatsächlich gibt es zwei mögliche Effekte: Verwenden der Karatsuba-Methode anstelle der normalen Multiplikation und das Auftreten zusätzlicher Abkürzungen, die Sie ausführen werden.

In einer Sekunde werden Sie sehen, wie es verwendet werden kann. Wenn Sie nun dieses Ergebnis für mod q erhalten und ein ähnliches Ergebnis für mod p erhalten, können Sie diese beiden Teile oben und unten endlich neu kombinieren und CRT, den chinesischen Restsatz, verwenden.

Und was Sie als Ergebnis von CRT erhalten ... Entschuldigung, ich denke, wir müssen dies zuerst aus dem Montgomery-Formular zurückkonvertieren. Daher konvertieren wir vor der Rekombination den oberen Teil in den Ausdruck (c ₀ ') ^d / R mod q und geben unseren Wert cd mod q zurück. Im unteren Teil erhalten wir dementsprechend cd mod p.

Jetzt können Sie CRT verwenden, um den Wert von c ^d mod n zu erhalten. Entschuldigung für die kleine Schrift, ich hatte nicht genug Tafel. Ungefähr das Gleiche bekommen wir hier unten mit ₁ , und wir können endlich unser Ergebnis erhalten, das heißt, Nachricht m.



Somit nimmt der Server ein eingehendes Paket, das er empfängt, führt es durch diese gesamte Pipeline, führt zwei Teile dieser Pipeline aus und endet mit einer entschlüsselten Nachricht m gleich cd mod m. Dann wird er die Polsterung dieses Beitrags überprüfen. Im Falle unseres spezifischen Angriffs haben wir so erstellt, dass dieser Zusatz tatsächlich nicht übereinstimmt. Wir haben den Wert c für Heuristiken gewählt, die die reale Nachricht nicht mit dem richtigen Auffüllzusatz verschlüsseln.

Daher besteht das Add-On den Test nicht. Der Server muss einen Fehler aufzeichnen, eine Fehlermeldung an den Client senden und die Verbindung trennen. Wir werden also die Zeit messen, die der Server benötigt, um unsere Nachricht durch diese Pipeline zu leiten. Haben Sie Fragen zum Prozess der Verarbeitung einer Nachricht durch den Server und zur Kombination all dieser Optimierungen?

Teilnehmerin: Meiner Meinung nach liegt ein Fehler mit einem Index der Größenordnung c vor.

Professor: Ja, Sie haben Recht, ich füge den Index 0 hinzu, hier sollte c ₀ ^d mod q sein.



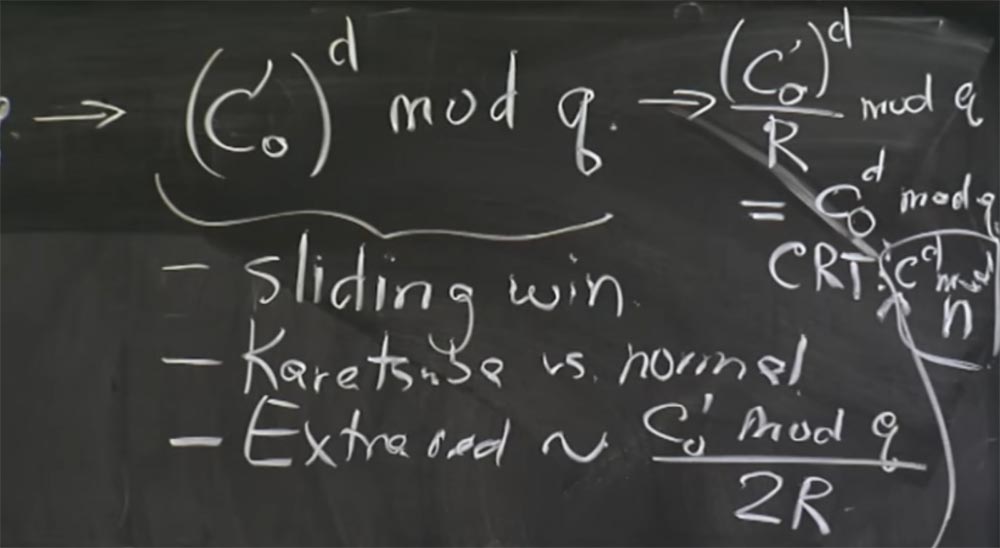Teilnehmerin: Wenn Sie durch R mod q dividieren, gibt es keine Annahmen darüber, wie viel q Sie hinzufügen sollten, um die niedrigen Bits weiter auf Nullen zu reduzieren?

Professor: Ja, Sie haben Recht, in dieser letzten Phase (c ₀ ') ^d / R mod q kann es zu zusätzlichen Reduzierungen kommen. Wir sollten also diese Division durch R auf die richtige Weise durchführen und wahrscheinlich dasselbe tun wie die Montgomery-Reduktion hier, wenn wir durch R dividieren, um den Wert zurück umzuwandeln. Da zu Beginn der Berechnungen nicht klar ist, wie viel q wir hinzufügen sollen, verwenden wir die Auswahlmethode, zerstören die niedrigen Nullen, machen dann erneut mod q und möglicherweise eine zusätzliche Reduktion. Sie sind absolut richtig, in diesem Fall ist es genau die gleiche Division durch R mod q wie für jeden Schritt der Montgomery-Multiplikation.

Wie nutzen Sie dies? Wie kann ein Angreifer den geheimen Schlüssel eines Servers lösen, indem er die Zeit misst, die zum Abschließen von Vorgängen benötigt wird? Diese Leute haben einen Plan, der darauf basiert, jeweils einen privaten Schlüssel zu erraten. Wir können davon ausgehen, dass der geheime Schlüssel der verschlüsselte Exponent d ist, da Sie e und n kennen, ist dies der öffentliche Schlüssel. Das einzige, was Sie nicht wissen, ist d.



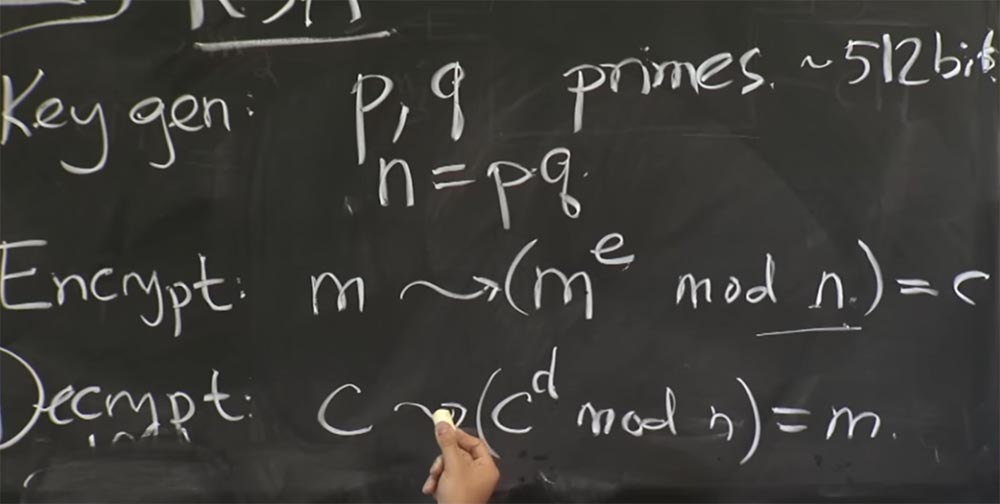
Tatsächlich erraten sie bei diesem Angriff den Wert von d nicht direkt, da er ziemlich kompliziert ist. Stattdessen betrachten sie q oder p, egal welche dieser beiden Größen. Sobald Sie erraten haben, worauf es bei p oder q ankommt, können Sie n = pq berechnen. Wenn Sie dann die Werte von p und q kennen, können Sie die Funktion φ berechnen, über die wir zuvor gesprochen haben. Auf diese Weise können Sie den Wert von d aus dem Wert von e erhalten. Daher ist diese Faktorisierung des Werts von n äußerst wichtig und muss geheim gehalten werden, um die RSA-Sicherheit zu gewährleisten.

Tatsächlich wollten diese Leute den q-Wert erraten, indem sie die Zeitabläufe dieser Pipeline analysierten. Was machen sie dafür? Sie wählen sorgfältig den Anfangswert des Werts von c aus und messen die Zeit seines Durchlaufs durch die Server-Pipeline.

Insbesondere besteht dieser Angriff aus zwei Teilen, und Sie müssen einige erste Schritte unternehmen, um die ersten paar Bits zu erraten. Sobald Sie die ersten Bits haben, können Sie das nächste Bit erraten. Lassen Sie mich daher nicht im Detail sagen, wie sie die ersten paar Bits erraten, da es in der Tat viel interessanter ist, zu überlegen, wie sie das nächste Bit erraten. Wenn wir Zeit haben, werden wir darauf zurückkommen, wie das Erraten mehrerer Anfangsbits in einem Vorlesungsartikel beschrieben wird.

Angenommen, Sie haben die Annahme g darüber, welche Bits im Wert dieses q enthalten sind. Dieser Wert bestehe aus solchen Bits: g = g ₀ g ₁ g ₂ ... und so weiter. Vielmehr ist es nicht einmal g, sondern die realen Teile von q. Lassen Sie es mich also so umschreiben: g = q ₀ q ₁ q ₂ .... Wir glauben, dass diese q hohe Bits sind, und wir versuchen, die Bits immer niedriger zu erraten. Angenommen, wir kennen den Wert von q bis zum Bit qj, und dann folgen alle Nullen. Sie haben keine Ahnung, was der Rest der Bits ist.



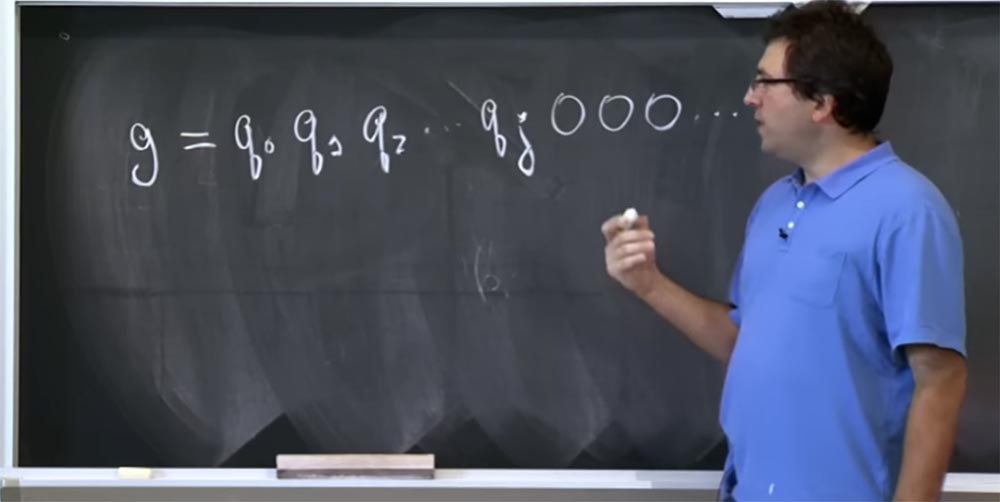
Diese Leute haben versucht, diese Vermutung g in diesen Ort unserer Pipeline zu injizieren: (c0 ') d mod q. Denn hier werden zwei Arten der Optimierung verwendet: die Karatsub-Methode anstelle der üblichen Multiplikation und eine unterschiedliche Anzahl zusätzlicher Abkürzungen in Abhängigkeit vom Wert von c ₀ '. Tatsächlich versuchten sie, zwei verschiedene Vermutungen an dieser Stelle der Pipeline einzuführen: die erste, die wie g = q ₀ q ₁ q ₂ ... qj 000 ... 0000 aussieht, und die zweite, die sie g _high nannten, die aus denselben hohen Bits besteht, aber stattdessen Von allen Nullen am Ende gibt es eine Einheit, die ein hohes Bit bezeichnet, gefolgt von erneut Nullen:

g = q ₀ q ₁ q ₂ ... qj 100 ... 0000.

Wie hilft das diesen Leuten zu verstehen, was passiert? Es gibt zwei Möglichkeiten, dies zu tun. Angenommen, unsere Vermutung g ist gleich dem Wert c ₀ '. Wir können annehmen, dass diese g und g _hoch dem auf der linken Tafel angegebenen Wert c ₀ 'entsprechen. Tatsächlich ist dies recht einfach, da c ₀ 'aus dem verschlüsselten Eingabewert c ₀ ziemlich einfach rückwärts zu berechnen ist. Sie multiplizieren es einfach mit R.



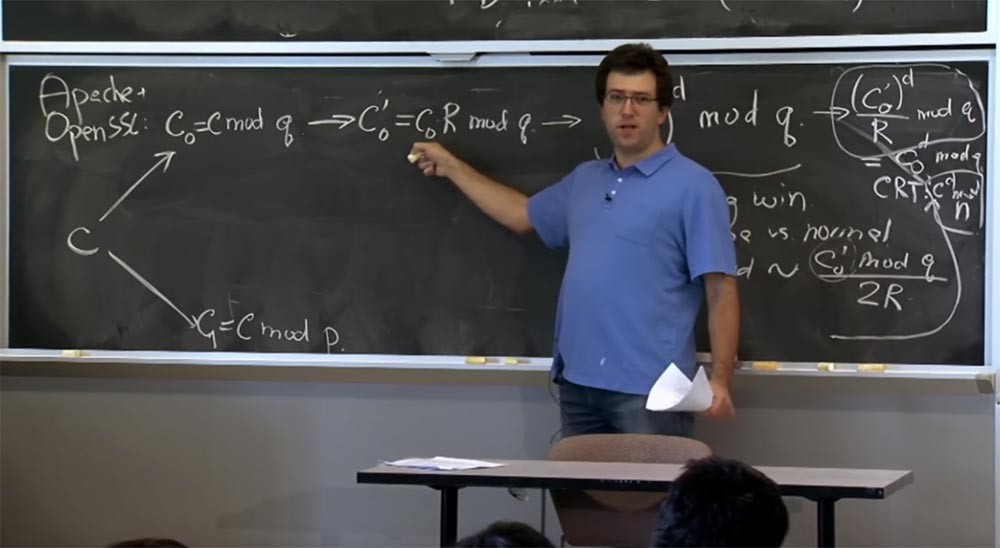
Um den Wert (c ₀ ') ^d zu erraten, müssen sie nur ihre Vermutung, ihre Vermutung g, nehmen und sie zuerst durch R teilen, dh durch 512 mod etwas dort teilen. Dann werden sie es wieder einführen, der Server wird es mit R multiplizieren und den in unserem Pipeline-Schema beschriebenen Prozess fortsetzen.

Angenommen, wir konnten unseren bestimmten ausgewählten ganzzahligen Wert an der richtigen Stelle platzieren. Was ist also die Rechenzeit c ₀ 'bis d mod q?



Es gibt zwei mögliche Optionen, bei denen q in dieses Bild passt. Es kann sein, dass q zwischen diesen beiden Werten von g und g _{hoch liegt} , weil das nächste Bit von q 0 ist. Somit ist dieser Wert - die erste 0 nach qj - kleiner als q, aber dieser Wert - 1 nach q - ist größer als q. Dies geschieht, wenn das nächste Bit von q 0 ist, oder es ist möglich, dass q über diesen beiden Werten liegt, wenn das nächste Bit von q 1 ist.



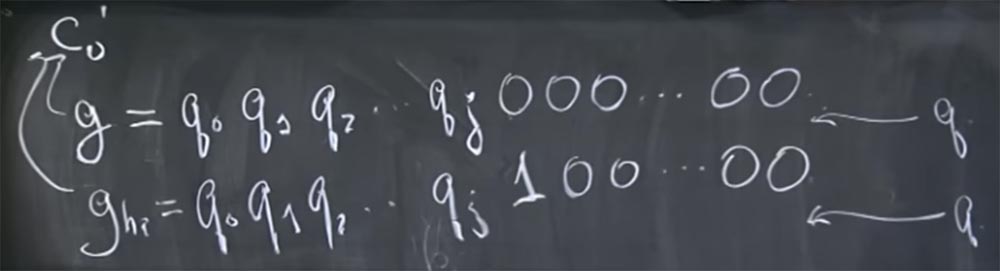
Nun können wir sagen, wie die Entschlüsselungszeit dieser beiden Werte sein wird, wenn q zwischen ihnen liegt oder wenn q über beiden liegt.

Schauen wir uns die Situation an, in der sich q oben befindet. In diesem Fall ist alles ziemlich gleich. Da diese beiden Werte kleiner als q sind, ist der Wert dieser Dinge in mod q ungefähr gleich. Sie unterscheiden sich aufgrund dieses zusätzlichen Bits geringfügig, sind aber immer noch mehr oder weniger gleich groß. Und die Anzahl der zusätzlichen Reduktionen, die zusätzliche Reduktion, wird sich wahrscheinlich auch nicht wesentlich unterscheiden, da sie proportional zum Wert von c0 'mod q ist. Und sowohl für g- als auch für g- _hohe Werte kleiner als q sind sie alle ungefähr gleich. Keiner von ihnen wird q überschreiten und keine große Anzahl zusätzlicher Reduzierungen verursachen, da für q, das größer als diese beiden Vermutungen ist, die Anzahl der Berechnungen nach der Karatsuba-Methode in Bezug auf die Anzahl der gewöhnlichen Berechnungen gleich bleibt. In Bezug auf diese Beziehung wird der Server sowohl g als auch g _high gleich behandeln. Daher wird der Server für beide Werte ungefähr die gleiche Anzahl zusätzlicher Abkürzungen vornehmen. Wenn Sie also feststellen, dass der Server dieselbe Zeit damit verbringt, auf diese Vermutungen zu reagieren, sollten Sie wahrscheinlich davon ausgehen, dass zu diesem Zeitpunkt tatsächlich 1 im g-Hochwert vorhanden ist.



Befindet sich andererseits q zwischen diesen beiden Werten, gibt es zwei mögliche Dinge, die zu Schalt- und Zeitänderungen führen können. Eines der Dinge ist, dass, da g _high etwas größer als q ist, die Anzahl der zusätzlichen Schnitte proportional zu c ₀ 'mod q ist, was sehr klein ist, da c ₀ ' q plus ein paar Bits in dieser zusätzlichen Bitfolge von 100 ... 00. Dadurch wird die Anzahl der zusätzlichen Reduzierungen deutlicher und alles beginnt schneller.
, , , , , : «, !». , g c ₀ ' , q, , g _high q, g _high mod q . , . – , , .

c ₀ ' mod q. c ₀ g _high , q, , g q. , . , , . , 32- , .

, 32- , , , . , . 32 , , - . , , 32, , , , .

, , , . , q 1, , q 0, , g _high q , , .

. , . , . , , 1-2 . , , Ethernet.
, . . , 7 . , , -, , ?

: ?

: , , , , , . , .

, , 7 , , 7 . 7 g, 7 g + 1, g + 2 7 g + 400. g, g, , 7 400, ?



: , , ?

: , , , — (c ₀ ') ^d . . , , , mod p. , , . , g, 1, 2, 3, , .

, , – 100…00. , mod p, , mod p . « », , (c ₀ ') ^d , . ?

: , ?

: - , q. , q, , , .

: c ₀ '?

: c ₀ ', c, c ₀ ' R mod n.



, «» , c ₀ = mod q, c ₀ = ((c ₀ ' R ^-1 ) mod n) mod q. R, R. c ₀ ', (c ₀ ') ^d mod q. , , , , R. , R = 2 ⁵¹² . , .

: mod p ?

: , , ? , ! , .


.

Vielen Dank für Ihren Aufenthalt bei uns. Gefällt dir unser Artikel? Möchten Sie weitere interessante Materialien sehen? Unterstützen Sie uns, indem Sie eine Bestellung aufgeben oder Ihren Freunden empfehlen, einen Rabatt von 30% für Habr-Benutzer auf ein einzigartiges Analogon von Einstiegsservern, das wir für Sie erfunden haben: Die ganze Wahrheit über VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s von $ 20 oder wie teilt man den Server? (Optionen sind mit RAID1 und RAID10, bis zu 24 Kernen und bis zu 40 GB DDR4 verfügbar).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 mal günstiger? Nur wir haben 2 x Intel Dodeca-Core Xeon E5-2650v4 128 GB DDR4 6 x 480 GB SSD 1 Gbit / s 100 TV von 249 US-Dollar in den Niederlanden und den USA! Lesen Sie mehr über den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro für einen Cent?