👨🏻‍🔬 👩🏿‍🎨 🎅🏽 Julia und die Bewegung eines geladenen Teilchens in einem elektromagnetischen Feld 👘 🙎🏼 🖐️

Wir stärken die Fähigkeiten zum Lösen und Visualisieren von Differentialgleichungen am Beispiel einer der gebräuchlichsten Evolutionsgleichungen, erinnern uns an das gute alte Scilab und versuchen zu verstehen, ob wir es brauchen ... Unter dem Schnittbild (Kilobyte für siebenhundert)

Stellen Sie sicher, dass die Software frisch ist

julia>] (v1.0) pkg>update #   (v1.0) pkg> status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.14.1+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Lassen Sie uns die früheren Anleitungen durchgehen

und fahren Sie mit der Erklärung des Problems fort

Die Bewegung geladener Teilchen in einem elektromagnetischen Feld

Auf einem geladenen Teilchen mit einer Ladung $q$ Bewegen in EMF mit Geschwindigkeit $u$ Die Lorentz-Kraft wirkt: $\ vec {F} _L = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right)$ . Diese Formel gilt mit einer Reihe von Vereinfachungen. Wenn wir Korrekturen an der Relativitätstheorie vernachlässigen, betrachten wir die Teilchenmasse als konstant, daher hat die Bewegungsgleichung die Form: $\ frac {d} {dt} (m \ vec {u}) = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right)$

Lassen Sie uns die Y-Achse entlang des elektrischen Feldes und die Z-Achse entlang des Magnetfelds lenken und der Einfachheit halber annehmen, dass die anfängliche Teilchengeschwindigkeit in der XY-Ebene liegt. In diesem Fall liegt auch die gesamte Flugbahn des Partikels in dieser Ebene. Die Bewegungsgleichungen haben folgende Form:

\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right.

$\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right.$

Unermesslich: $x ^ * = \ frac {x} {\ lambda}, \, y ^ * = \ frac {y} {\ lambda}, \, \ tau = \ frac {ct} {\ lambda}, \, B ^ * = \ frac {Bmc} {q \ lambda}, \, E ^ * = \ frac {Emc ^ 2} {q \ lambda}$ . Sternchen geben Maßgrößen an und $\ lambda$ - die charakteristische Größe des betrachteten physikalischen Systems. Wir erhalten ein dimensionsloses System von Bewegungsgleichungen eines geladenen Teilchens in einem Magnetfeld:

\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right.

$\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right.$

Lassen Sie uns die Reihenfolge senken:

\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ right.

$\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ right.$

Als Erstkonfiguration des Modells wählen wir: $B = 2$ T. $E = 5 \ cdot 10 ^ 4$ V / m $v_0 = 7 \ cdot 10 ^ 4$ m / s Für eine numerische Lösung verwenden wir das Paket DifferentialEquations :

Code und Grafiken

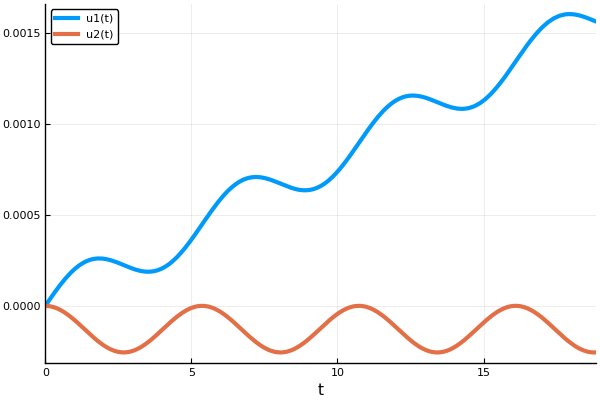
 using DifferentialEquations, Plots pyplot() M = 9.11e-31 # kg q = 1.6e-19 # C C = 3e8 # m/s λ = 1e-3 # m function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4) B = Bo*q*λ / (M*C) E = Eo*q*λ / (M*C*C) vel /= C A = [0. 0. 1. 0.; 0. 0. 0. 1.; 0. 0. 0. B; 0. 0. -B 0.] syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system u0 = [0.0; 0.0; vel; 0.0] # start cond-ns tspan = (0.0, 6pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000) end Solut = modelsolver() plot(Solut)

Hier verwenden wir die Euler-Methode, für die die Anzahl der Schritte angegeben ist. Außerdem wird nicht die gesamte Lösung des Systems in der Antwortmatrix gespeichert, sondern nur 1 und 2 Indizes, dh die Koordinaten des X und des Spielers (wir benötigen keine Geschwindigkeiten).

 X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")#

Überprüfen Sie das Ergebnis. Wir führen eine neue Variable anstelle von x ein $\ tilde {x} = x-ut$ . Somit wird ein Übergang zu einem neuen Koordinatensystem vorgenommen, das sich relativ zum Original mit einer Geschwindigkeit u in Richtung der X- Achse bewegt:

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrix} \ right.

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrix} \ right.$

Wenn Sie möchten $u = E / B$ und bezeichnen $\ omega = qB / m$ , dann wird das System vereinfacht:

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { Matrix} \ rechts.

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { Matrix} \ rechts.$

Das elektrische Feld ist aus den letzten Gleichungen verschwunden und es handelt sich um die Bewegungsgleichungen eines Teilchens unter dem Einfluss eines gleichmäßigen Magnetfelds. Daher sollte sich das Teilchen im neuen Koordinatensystem (x, y) in einem Kreis bewegen. Da sich dieses neue Koordinatensystem selbst relativ zum Original mit Geschwindigkeit bewegt $u = E / B$ Dann besteht die resultierende Partikelbewegung aus einer gleichmäßigen Bewegung entlang der X- Achse und einer Drehung um den Kreis in der XY- Ebene. Wie Sie wissen, ist die Flugbahn, die auftritt, wenn diese beiden Bewegungen addiert werden, im Allgemeinen ein Trochoide . Insbesondere wenn die Anfangsgeschwindigkeit Null ist, wird der einfachste Fall einer solchen Bewegung realisiert - entlang der Zykloide .
Stellen wir sicher, dass die Driftgeschwindigkeit wirklich gleich E / V ist. Dafür:

Wir verderben die Antwortmatrix, indem wir anstelle des ersten Elements (Maximum) einen absichtlich niedrigeren Wert festlegen.
Wir finden die Nummer des maximalen Elements in der zweiten Spalte der Antwortmatrix, die durch die Ordinate verzögert wird
Wir berechnen die dimensionslose Driftgeschwindigkeit, indem wir den maximalen Abszissenwert durch den entsprechenden Zeitwert dividieren

 Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]

Out: 8.334546850446588e-5

 B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B

Out: 8.333333333333333332e-5
Bis zur siebten Bestellung!
Der Einfachheit halber definieren wir eine Funktion, die die Modellparameter und die Signatur des Diagramms übernimmt und gleichzeitig als Name der im Projektordner erstellten PNG- Datei dient (funktioniert in Juno / Atom und Jupyter). Im Gegensatz zu Gadfly , wo Diagramme in Ebenen erstellt und dann von der Funktion plot () angezeigt wurden, wird in Plots zum Erstellen verschiedener Diagramme in einem Frame das erste von der Funktion plot () erstellt , und die nachfolgenden Diagramme werden mit plot! () Hinzugefügt. Die Namen von Funktionen, die die akzeptierten Objekte in Julia ändern, enden üblicherweise mit einem Ausrufezeichen.

 function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end

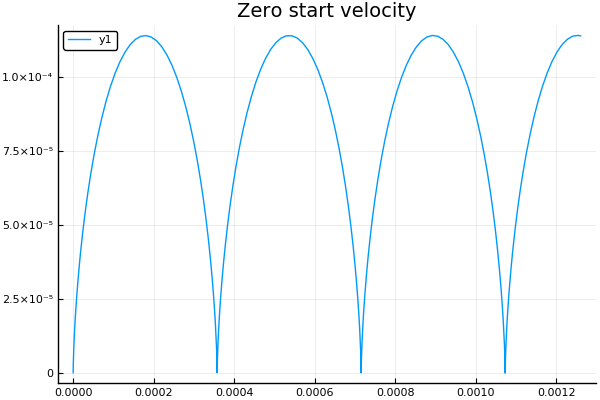
Wie erwartet erhalten wir bei einer Anfangsgeschwindigkeit von Null eine Zykloide :

 plot() plotter("Zero start velocity", 2, 4e4, 7e4)

Wir erhalten die Flugbahn des Teilchens, wenn sich die Induktion, Intensität und das Ladungszeichen ändern. Ich möchte Sie daran erinnern, dass ein Punkt die sequentielle Ausführung einer Funktion mit allen Elementen des Arrays bedeutet

Versteckt

 plot() plotter.("B   ", 0, [3e4 4e4 5e4 6e4] )

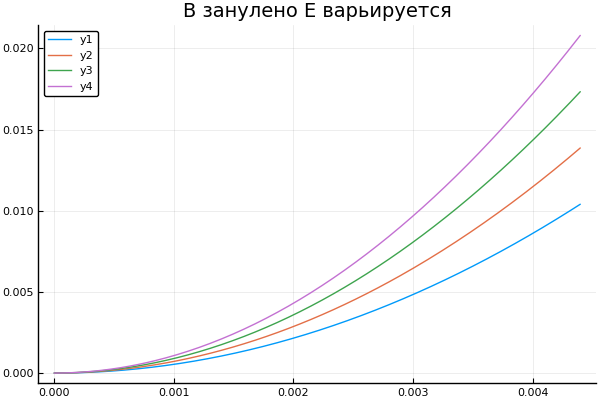
 plot() plotter.("E  B ", [1 2 3 4], 0 )

 q = -1.6e-19 # C plot() plotter.(" ")

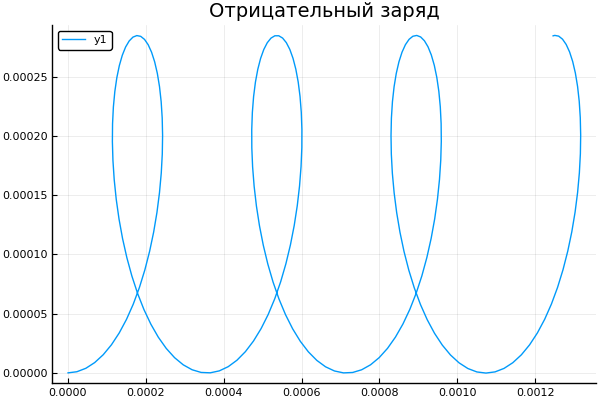
Und lassen Sie uns sehen, wie sich die Änderung der Anfangsgeschwindigkeit auf die Flugbahn des Partikels auswirkt:

 plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )

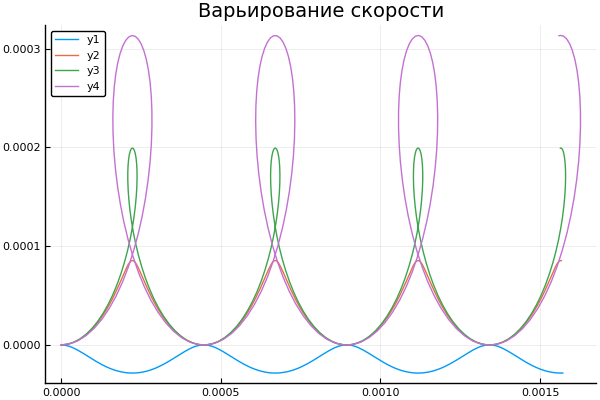
Ein bisschen über Scilab

Auf Habré gibt es bereits genügend Informationen über Silab, zum Beispiel 1 , 2 , und hier über Octave beschränken wir uns daher auf Links zu Wikipedia und zur Homepage .

Ich selbst möchte das Vorhandensein einer praktischen Benutzeroberfläche mit Kontrollkästchen, Schaltflächen und Grafiken sowie ein ziemlich interessantes visuelles Modellierungswerkzeug von Xcos hinzufügen. Letzteres kann beispielsweise verwendet werden, um ein Signal in der Elektrotechnik zu simulieren:

Spoiler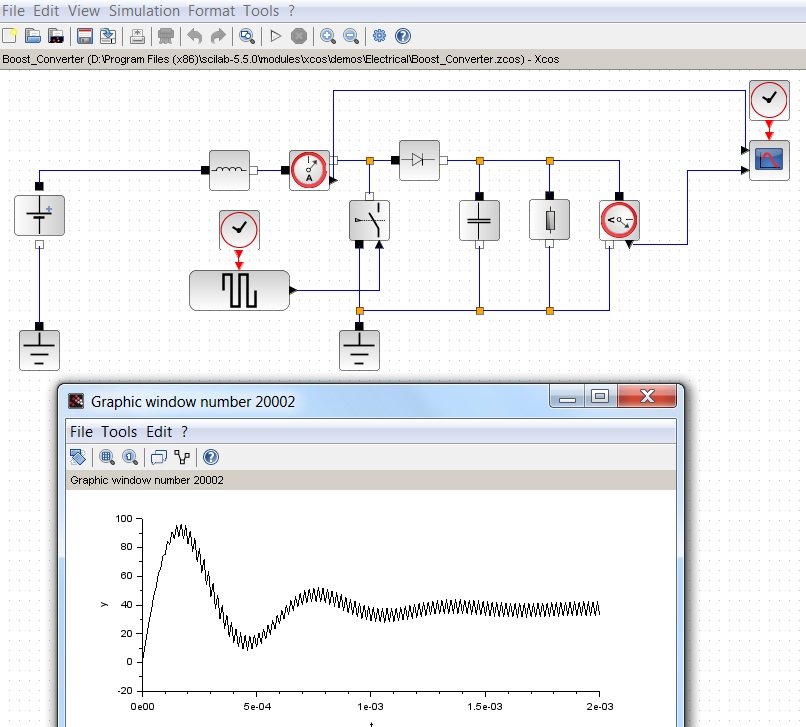

Und hier ist eine sehr praktische Anleitung:

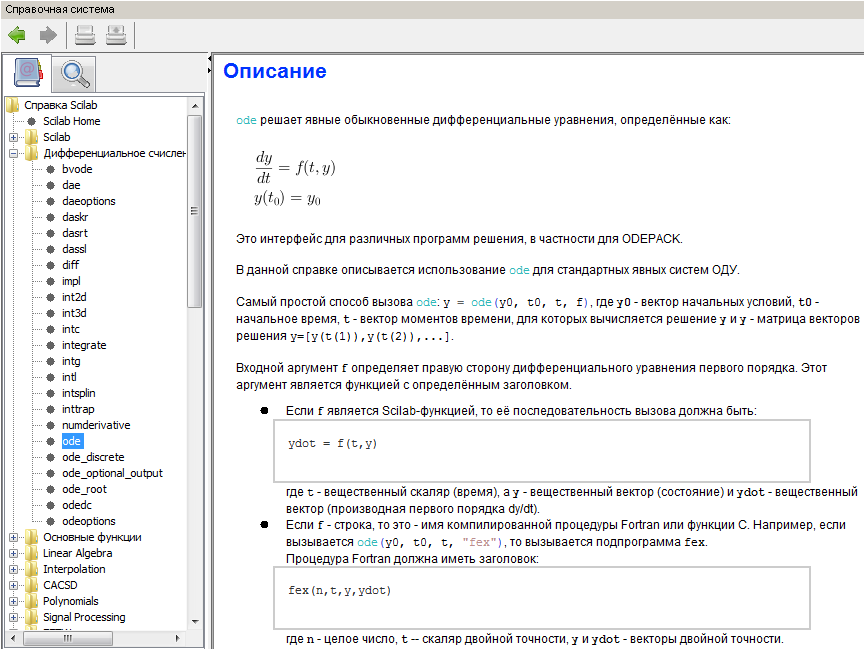
Tatsächlich kann unsere Aufgabe auch in Scilab gelöst werden:

Code und Bilder

 clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle ("   ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)//    plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');//       xs2jpg(1,'graf2');// ,  -

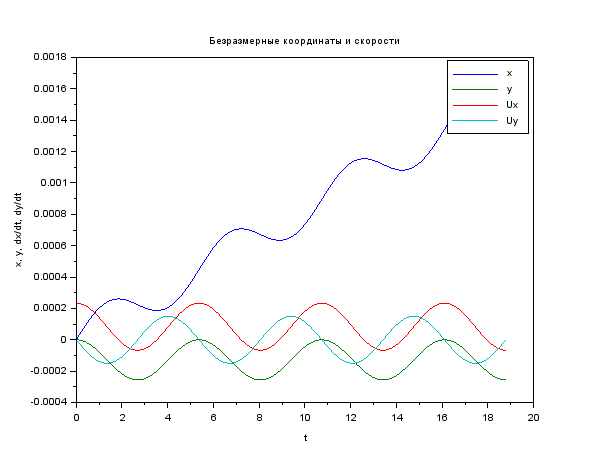
Hier finden Sie Informationen zur Funktion zum Lösen von Odenunterschieden . Grundsätzlich stellt sich die Frage

Warum brauchen wir Julia?

... wenn es so wundervolle Dinge wie Scilab, Octave und Numpy, Scipy gibt?
Über die letzten beiden werde ich nicht sagen - ich habe es nicht versucht. Und im Allgemeinen ist die Frage kompliziert, also werfen wir einen kurzen Blick darauf:

Scilab
Auf einer Festplatte dauert es etwas mehr als 500 MB, es startet schnell und sofort stehen Differentialberechnungen, Grafiken und alles andere zur Verfügung. Gut für Anfänger: Ein ausgezeichneter Führer (meistens lokalisiert), es gibt viele Bücher in russischer Sprache. Über interne Fehler wurde hier und hier bereits gesprochen , und da das Produkt sehr nisch ist, ist die Community träge und zusätzliche Module sind sehr selten.

Julia
Wenn Pakete hinzugefügt werden (insbesondere Python-a-la-Jupyter und Mathplotlib), wächst sie von 376 MB auf etwas mehr als sechs Gigabyte. Sie spart auch keinen Arbeitsspeicher: Zu Beginn von 132 MB und nach dem Plotten von Zeitplänen in Jupiter wird es ruhig 1 GB erreichen. Wenn Sie in Juno arbeiten , ist alles fast wie in Scilab : Sie können den Code sofort im Interpreter ausführen, Sie können den integrierten Editor ausdrucken und als Datei speichern, es gibt einen variablen Browser, ein Befehlsprotokoll und eine Online-Hilfe. Persönlich bin ich empört über das Fehlen von clear () , das heißt, ich habe den Code gestartet, ihn dann korrigiert und umbenannt, und die alten Variablen sind geblieben (es gibt keinen Variablenbrowser in Jupiter).

Aber das alles ist nicht kritisch. Scilab ist sehr gut für das erste Paar geeignet. Eine Stirn, einen Cursor oder etwas dazwischen zu berechnen, ist ein sehr improvisiertes Werkzeug. Es gibt zwar auch Unterstützung für paralleles Rechnen und Aufrufen von Sishn / Fortran-Funktionen, für die es nicht ernsthaft verwendet werden kann. Große Arrays erschrecken ihn, um mehrdimensionale Arrays festzulegen, muss man sich mit allen Arten von Obskurantismus auseinandersetzen , und Berechnungen, die über den Rahmen klassischer Aufgaben hinausgehen, können durchaus alles zusammen mit dem Betriebssystem fallen lassen.

Und nach all diesen Schmerzen und Enttäuschungen können Sie sicher zu Julia wechseln, um auch hier zu harken. Wir werden weiter studieren, der Nutzen der Community ist sehr reaktionsschnell, Probleme lösen sich schnell und Julia hat viele weitere interessante Funktionen, die den Lernprozess zu einer aufregenden Reise machen werden!

Julia und die Bewegung eines geladenen Teilchens in einem elektromagnetischen Feld

Die Bewegung geladener Teilchen in einem elektromagnetischen Feld

Ein bisschen über Scilab

Warum brauchen wir Julia?

More articles: