Also ein weiterer Artikel aus dem Zyklus
„Mathe an den Fingern “. Heute setzen wir
die Diskussion über Methoden der kleinsten Quadrate fort, diesmal jedoch aus Sicht des Programmierers. Dies ist ein weiterer Artikel in der Reihe, der sich jedoch von anderen abhebt, da er im Allgemeinen keine mathematischen Kenntnisse erfordert. Der Artikel wurde als Einführung in die Theorie konzipiert. Daher erfordert er aufgrund seiner Grundkenntnisse die Fähigkeit, einen Computer einzuschalten und fünf Codezeilen zu schreiben. Natürlich werde ich mich nicht mit diesem Artikel befassen und in naher Zukunft eine Fortsetzung veröffentlichen. Wenn ich genug Zeit finde, werde ich aus diesem Material ein Buch schreiben. Die Zielgruppe sind Programmierer, daher ist Habr der richtige Ort, um einzusteigen. Im Allgemeinen schreibe ich nicht gerne Formeln, und ich lerne sehr gerne aus Beispielen. Es scheint mir, dass dies sehr wichtig ist - schauen Sie sich nicht nur die Schnörkel auf der Schulbehörde an, sondern probieren Sie alles auf den Zahn.
Also fangen wir an. Stellen wir uns vor, ich habe eine triangulierte Oberfläche mit einem Scan meines Gesichts (im Bild links). Was muss ich tun, um die Funktionen zu verbessern und diese Oberfläche in eine groteske Maske zu verwandeln?
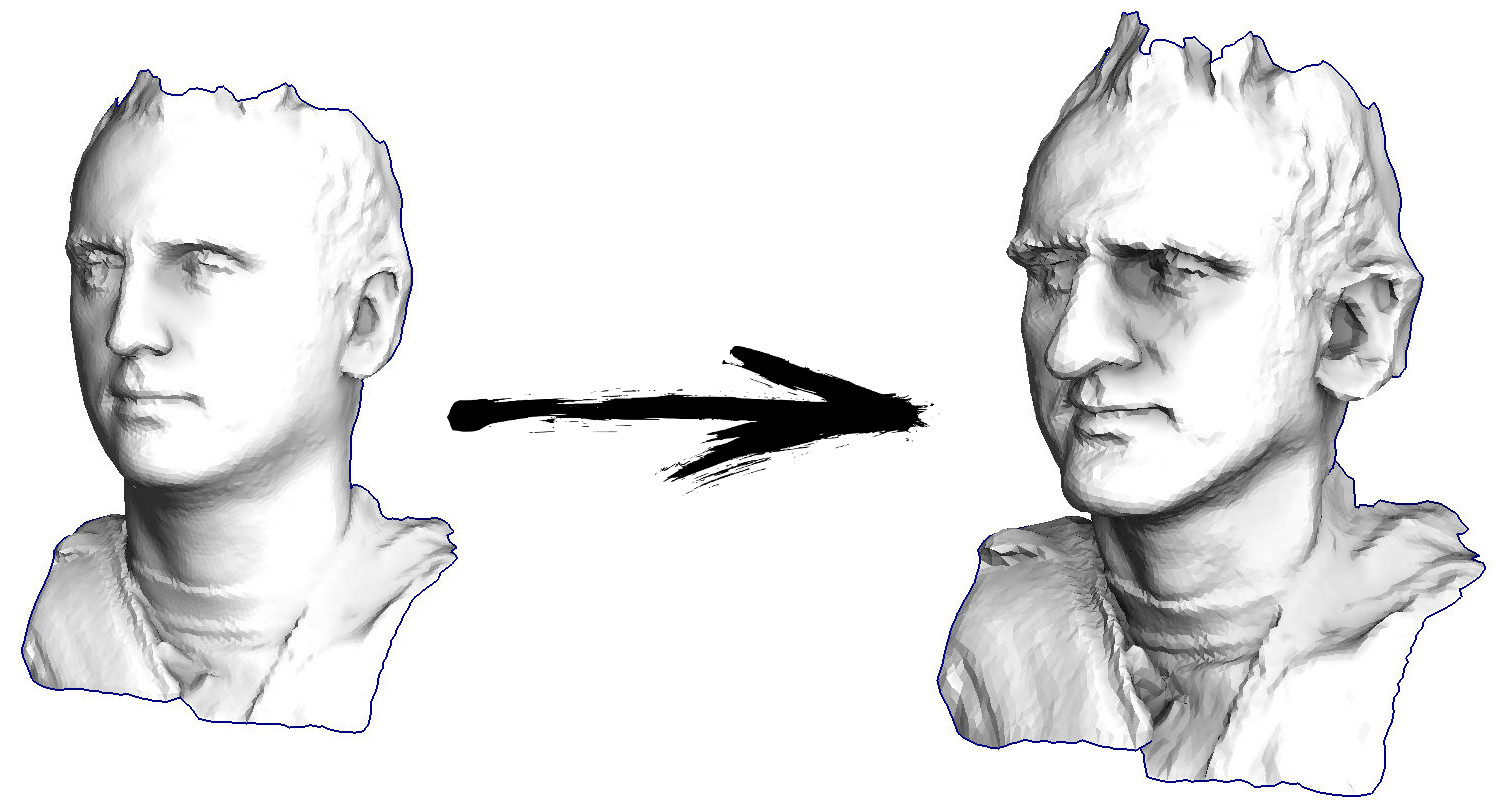
In diesem speziellen Fall löse ich eine elliptische Differentialgleichung namens
Simeon Demi Poisson . Mitprogrammierer, lassen Sie uns ein Spiel spielen: Ratet mal, wie viele Zeilen im C ++ - Code es gibt, die darüber entscheiden? Bibliotheken von Drittanbietern können nicht aufgerufen werden, wir verfügen nur über einen Bare-Compiler. Die Antwort ist unter dem Schnitt.
Tatsächlich reichen zwanzig Codezeilen für einen Löser aus. Wenn Sie mit allem zählen, alles, einschließlich des Parsers der 3D-Modelldatei, halten Sie sich innerhalb von zweihundert Zeilen - spucken Sie einfach.
Beispiel 1: Datenglättung
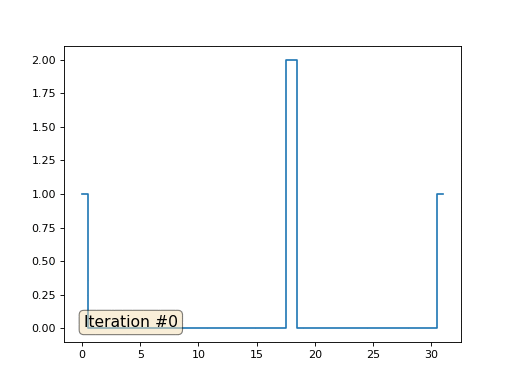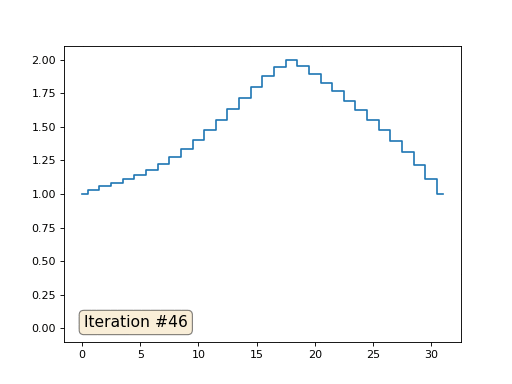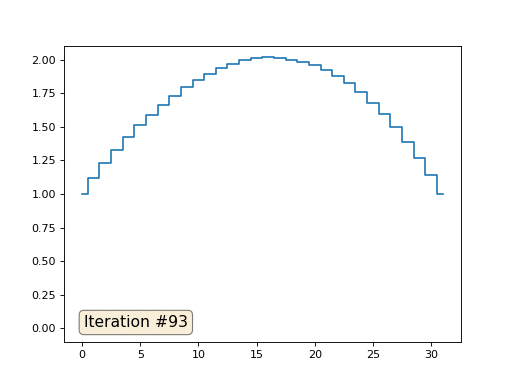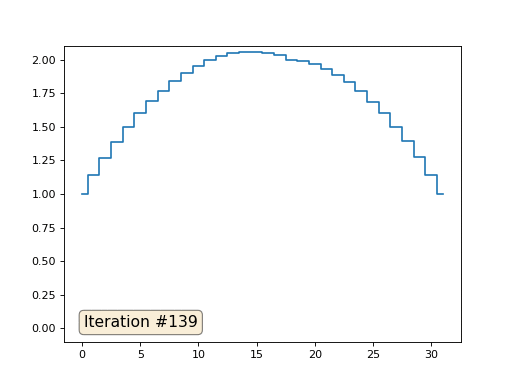
Sprechen wir darüber, wie es funktioniert. Beginnen wir von weitem und stellen wir uns vor, wir haben ein reguläres Array f, zum Beispiel aus 32 Elementen, das wie folgt initialisiert wird:

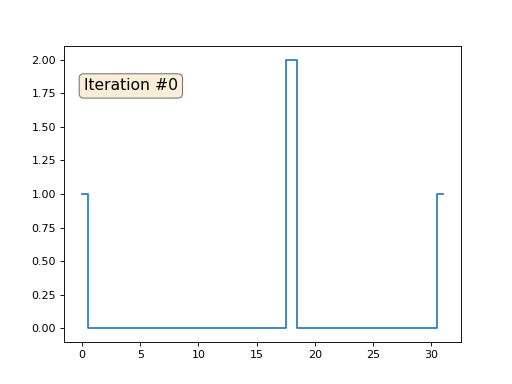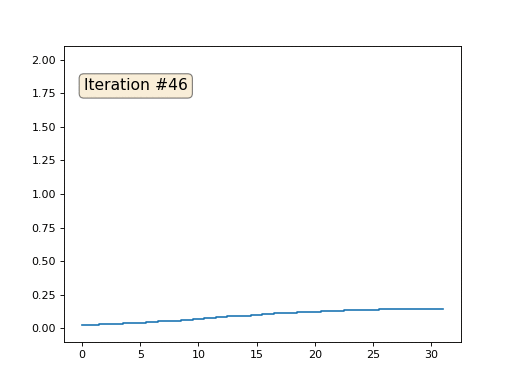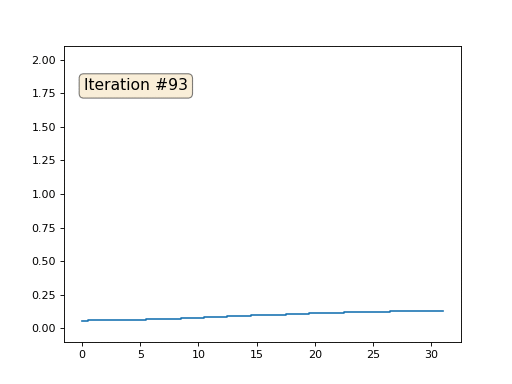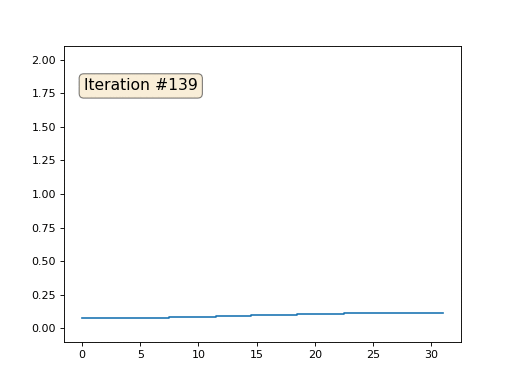
Und dann führen wir die folgende Prozedur tausendmal durch: Für jede Zelle f [i] schreiben wir den Durchschnittswert benachbarter Zellen hinein: f [i] = (f [i-1] + f [i + 1]) / 2. Um es klarer zu machen, hier ist der vollständige Code:
import matplotlib.pyplot as plt f = [0.] * 32 f[0] = f[-1] = 1. f[18] = 2. plt.plot(f, drawstyle='steps-mid') for iter in range(1000): f[0] = f[1] for i in range(1, len(f)-1): f[i] = (f[i-1]+f[i+1])/2. f[-1] = f[-2] plt.plot(f, drawstyle='steps-mid') plt.show()
Jede Iteration glättet die Daten unseres Arrays und nach tausend Iterationen erhalten wir in allen Zellen einen konstanten Wert. Hier ist eine Animation der ersten 150 Iterationen:
Wenn Ihnen nicht klar ist, warum Anti-Aliasing auftritt, hören Sie sofort auf, greifen Sie zu einem Stift und versuchen Sie, Beispiele zu zeichnen. Andernfalls ist es nicht sinnvoll, weiterzulesen. Die triangulierte Oberfläche ist im Wesentlichen dieselbe wie in diesem Beispiel. Stellen Sie sich vor, wir finden für jeden Scheitelpunkt seine Nachbarn, berechnen ihren Massenschwerpunkt und verschieben unseren Scheitelpunkt zehnmal auf diesen Massenschwerpunkt. Das Ergebnis wird folgendermaßen aussehen:

Wenn Sie nicht bei zehn Iterationen anhalten, wird nach einer Weile die gesamte Oberfläche auf genau die gleiche Weise wie im vorherigen Beispiel auf einen Punkt komprimiert, und das gesamte Array wurde mit demselben Wert gefüllt.
Beispiel 2: Verbessern / Dämpfen von Funktionen
Der vollständige Code
ist auf dem Github verfügbar , aber hier werde ich den wichtigsten Teil geben, wobei nur das Lesen und Schreiben von 3D-Modellen weggelassen wird. Das triangulierte Modell wird für mich also durch zwei Arrays dargestellt: Verts und Gesichter. Das Verts-Array ist nur eine Menge dreidimensionaler Punkte, sie sind die Eckpunkte des Polygonnetzes. Das Flächenarray besteht aus einer Reihe von Dreiecken (die Anzahl der Dreiecke entspricht den Flächen.size ()). Für jedes Dreieck werden die Indizes aus dem Scheitelpunktarray im Array gespeichert. Das Datenformat und die Arbeit damit habe ich in
meinen Vorlesungen über Computergrafik ausführlich beschrieben. Es gibt auch ein drittes Array, das ich aus den ersten beiden (genauer gesagt nur aus dem Flächen-Array) wiedergebe - vvadj. Dies ist ein Array, das für jeden Scheitelpunkt (den ersten Index eines zweidimensionalen Arrays) die Indizes seiner Nachbarn speichert (zweiter Index).
std::vector<Vec3f> verts; std::vector<std::vector<int> > faces; std::vector<std::vector<int> > vvadj;
Als erstes betrachte ich für jeden Scheitelpunkt meiner Oberfläche den Krümmungsvektor. Lassen Sie uns veranschaulichen: Für den aktuellen Scheitelpunkt v iteriere ich über alle seine Nachbarn n1-n4; dann zähle ich ihren Massenschwerpunkt b = (n1 + n2 + n3 + n4) / 4. Nun, der endgültige Krümmungsvektor kann als c = vb berechnet werden, es ist nichts anderes als
gewöhnliche endliche Differenzen für die zweite Ableitung .

Direkt im Code sieht es so aus:
std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0)); for (int i=0; i<(int)verts.size(); i++) { for (int j=0; j<(int)vvadj[i].size(); j++) { curvature[i] = curvature[i] - verts[vvadj[i][j]]; } curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size(); }
Nun, dann machen wir das Folgende viele Male (siehe vorheriges Bild): Wir verschieben den Scheitelpunkt v nach v: = b + const * c. Bitte beachten Sie, dass sich unser Scheitelpunkt nirgendwo bewegt, wenn die Konstante gleich eins ist! Wenn die Konstante Null ist, wird der Scheitelpunkt durch den Schwerpunkt der benachbarten Scheitelpunkte ersetzt, wodurch unsere Oberfläche geglättet wird. Wenn die Konstante größer als Eins ist (das Titelbild wurde mit const = 2.1 erstellt), verschiebt sich der Scheitelpunkt in Richtung des Oberflächenkrümmungsvektors, wodurch die Details verstärkt werden. So sieht es im Code aus:
for (int it=0; it<100; it++) { for (int i=0; i<(int)verts.size(); i++) { Vec3f bary(0,0,0); for (int j=0; j<(int)vvadj[i].size(); j++) { bary = bary + verts[vvadj[i][j]]; } bary = bary / (float)vvadj[i].size(); verts[i] = bary + curvature[i]*2.1;
Übrigens, wenn es kleiner als eins ist, werden die Details im Gegenteil schwächer (const = 0,5), aber dies ist nicht gleichbedeutend mit einer einfachen Glättung, der "Bildkontrast" bleibt:

Bitte beachten Sie, dass mein Code eine 3D-Modelldatei im
Wavefront-OBJ- Format
generiert , die ich in einem Drittanbieterprogramm gerendert habe. Sie können das resultierende Modell beispielsweise im
Online-Viewer sehen . Wenn Sie an den Rendering-Methoden interessiert sind, anstatt das Modell zu generieren, lesen Sie meinen
Kurs über Computergrafik .
Beispiel 3: Hinzufügen von Einschränkungen
Kehren wir zum allerersten Beispiel zurück und machen genau das Gleiche, schreiben aber die Elemente des Arrays nicht unter den Nummern 0, 18 und 31 neu:
import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. plt.plot(x, drawstyle='steps-mid') plt.show()
Ich habe die restlichen "freien" Elemente des Arrays mit Nullen initialisiert und sie dennoch iterativ durch den Durchschnittswert benachbarter Elemente ersetzt. So sieht die Entwicklung des Arrays in den ersten 150 Iterationen aus:

Es ist ziemlich offensichtlich, dass die Lösung diesmal nicht zu einem konstanten Element konvergiert, das das Array füllt, sondern zu zwei linearen Rampen. Ist es übrigens wirklich für alle offensichtlich? Wenn nicht, experimentieren Sie mit diesem Code. Ich gebe speziell Beispiele mit einem sehr kurzen Code, damit Sie genau verstehen können, was passiert.
Lyrischer Exkurs: numerische Lösung linearer Gleichungssysteme.
Geben wir das übliche lineare Gleichungssystem an:

Es kann umgeschrieben werden, wobei in jeder der Gleichungen eine Seite des Gleichheitszeichens x_i verbleibt:
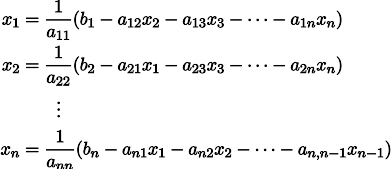
Geben wir einen beliebigen Vektor an

Annäherung an die Lösung eines Gleichungssystems (z. B. Null).
Wenn wir es dann auf die rechte Seite unseres Systems kleben, können wir einen aktualisierten Lösungsnäherungsvektor erhalten

.
Um es klarer zu machen, wird x1 wie folgt aus x0 erhalten:
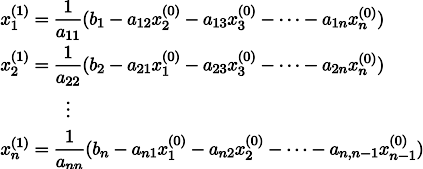
Wenn Sie den Vorgang k-mal wiederholen, wird die Lösung durch den Vektor angenähert
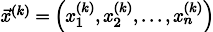
Schreiben wir für alle Fälle eine Rekursionsformel:
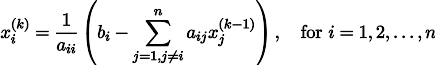
Unter einigen Annahmen über die Koeffizienten des Systems (zum Beispiel ist es offensichtlich, dass die diagonalen Elemente nicht Null sein sollten, weil wir sie teilen), konvergiert diese Prozedur zur wahren Lösung. Diese Gymnastik ist in der Literatur als
Jacobi-Methode bekannt . Natürlich gibt es andere Methoden zum numerischen Lösen linearer Gleichungssysteme und viel leistungsfähigere, zum Beispiel
die konjugierte Gradientenmethode , aber vielleicht ist die Jacobi-Methode eine der einfachsten.
Wieder Beispiel 3, aber auf der anderen Seite
Schauen wir uns nun die Hauptschleife aus Beispiel 3 genauer an:
for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2.
Ich habe mit einem anfänglichen Vektor x begonnen und ihn tausendmal aktualisiert, und die Aktualisierungsprozedur ähnelt verdächtig der Jacobi-Methode! Schreiben wir dieses Gleichungssystem explizit:

Nehmen Sie sich etwas Zeit und stellen Sie sicher, dass jede Iteration in meinem Python-Code nur eine Aktualisierung der Jacobi-Methode für dieses Gleichungssystem ist. Die Werte x [0], x [18] und x [31] sind für mich festgelegt, sie sind nicht im Variablensatz enthalten, daher werden sie auf die rechte Seite übertragen.
Insgesamt sehen alle Gleichungen in unserem System aus wie - x [i-1] + 2 x [i] - x [i + 1] = 0. Dieser Ausdruck ist nichts anderes als
gewöhnliche endliche Differenzen für die zweite Ableitung . Das heißt, unser Gleichungssystem schreibt einfach vor, dass die zweite Ableitung überall gleich Null sein muss (außer am Punkt x [18]). Denken Sie daran, ich sagte, dass es offensichtlich ist, dass Iterationen zu linearen Rampen konvergieren sollten? Genau deshalb ist die lineare Ableitung der zweiten Ableitung Null.
Wissen Sie, dass wir gerade
das Dirichlet-Problem für die Laplace-Gleichung gelöst haben?
Übrigens sollte ein aufmerksamer Leser bemerkt haben, dass in meinem Code streng genommen lineare Gleichungssysteme nicht nach der Jacobi-Methode, sondern
nach der Gauß-Seidel-Methode gelöst
werden , die eine Art Optimierung der Jacobi-Methode darstellt:
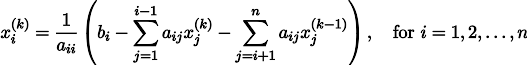
Beispiel 4: Poisson-Gleichung
Und lassen Sie uns das dritte Beispiel ein wenig ändern: Jede Zelle befindet sich nicht nur im Massenmittelpunkt benachbarter Zellen, sondern im Massenmittelpunkt
plus einer (willkürlichen) Konstante: import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1] +11./32**2 )/2. plt.plot(x, drawstyle='steps-mid') plt.show()
Im vorherigen Beispiel haben wir festgestellt, dass das Platzieren im Massenschwerpunkt die Diskretisierung des Laplace-Operators ist (in unserem Fall die zweite Ableitung). Das heißt, jetzt lösen wir ein Gleichungssystem, das besagt, dass unser Signal eine konstante zweite Ableitung haben muss. Die zweite Ableitung ist die Krümmung der Oberfläche; Daher sollte eine stückweise quadratische Funktion die Lösung für unser System sein. Lassen Sie uns die Probenahme in 32 Proben überprüfen:
Mit einer Array-Länge von 32 Elementen konvergiert unser System in ein paar hundert Iterationen zu einer Lösung. Aber was ist, wenn wir ein Array von 128 Elementen ausprobieren? Hier ist alles viel trauriger, die Anzahl der Iterationen muss bereits in Tausenden berechnet werden:
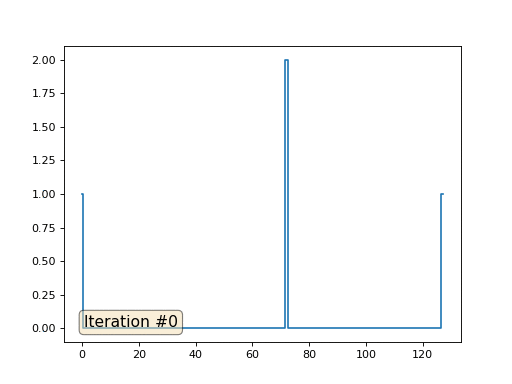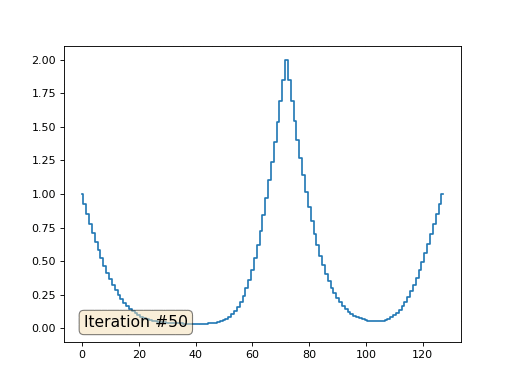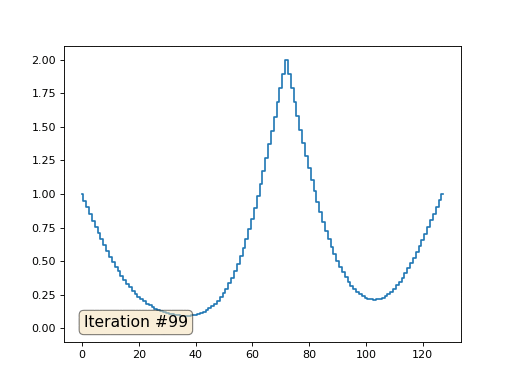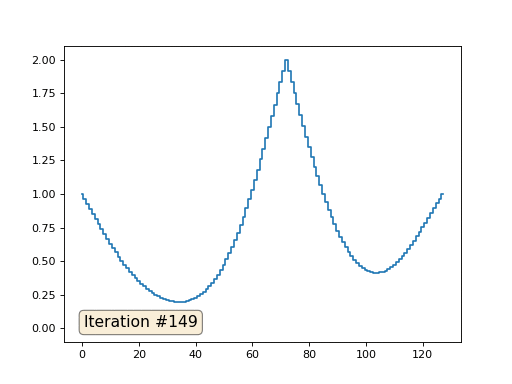
Die Gauß-Seidel-Methode ist äußerst einfach zu programmieren, jedoch nicht für große Gleichungssysteme anwendbar. Sie können versuchen, es zu beschleunigen, indem Sie beispielsweise
Multigrid-Methoden verwenden . Mit anderen Worten, das mag umständlich klingen, aber die Idee ist äußerst primitiv: Wenn wir eine Lösung mit einer Auflösung von tausend Elementen wollen, können wir zuerst mit zehn Elementen lösen, eine grobe Annäherung erhalten, dann die Auflösung verdoppeln, sie erneut lösen und so weiter, bis wir sie erreichen gewünschtes Ergebnis. In der Praxis sieht es so aus:
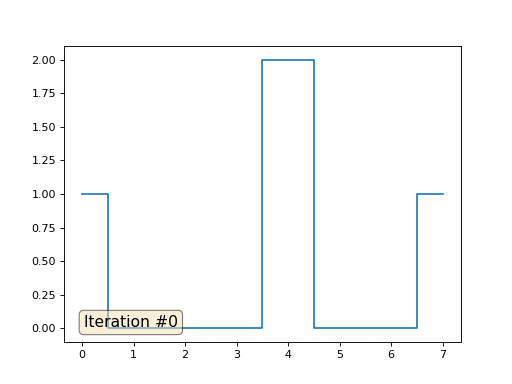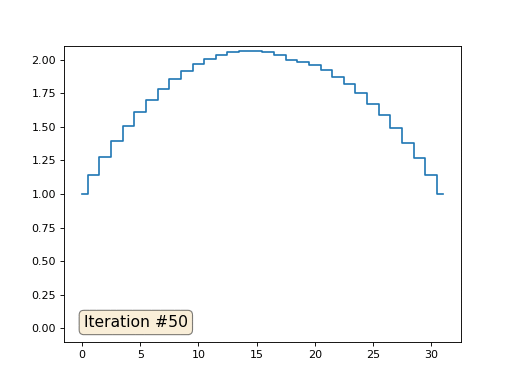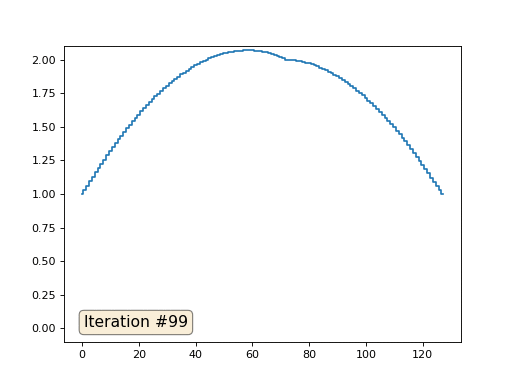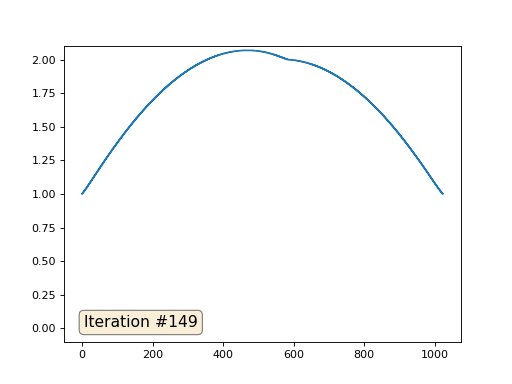
Und Sie können nicht angeben und echte Löser von Gleichungssystemen verwenden. Also löse ich das gleiche Beispiel, indem ich die Matrix A und die Spalte b konstruiere und dann die Matrixgleichung Ax = b löse:
import numpy as np import matplotlib.pyplot as plt n=1000 x = [0.] * n x[0] = x[-1] = 1. m = n*57//100 x[m] = 2. A = np.matrix(np.zeros((n, n))) for i in range(1,n-2): A[i, i-1] = -1. A[i, i] = 2. A[i, i+1] = -1. A = A[1:-2,1:-2] A[m-2,m-1] = 0 A[m-1,m-2] = 0 b = np.matrix(np.zeros((n-3, 1))) b[0,0] = x[0] b[m-2,0] = x[m] b[m-1,0] = x[m] b[-1,0] = x[-1] for i in range(n-3): b[i,0] += 11./n**2 x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0]) x2.insert(0, x[0]) x2.insert(m, x[m]) x2.append(x[-1]) plt.plot(x2, drawstyle='steps-mid') plt.show()
Und hier ist das Ergebnis der Arbeit dieses Programms. Beachten Sie, dass sich die Lösung sofort herausstellte:

Somit ist unsere Funktion tatsächlich stückweise quadratisch (die zweite Ableitung ist konstant). Im ersten Beispiel setzen wir die zweite zweite Ableitung auf Null, die dritte ungleich Null, aber überall gleich. Und was war im zweiten Beispiel? Wir haben die
diskrete Poisson-Gleichung durch Angabe der Krümmung der Oberfläche gelöst. Ich möchte Sie daran erinnern, was passiert ist: Wir haben die Krümmung der ankommenden Oberfläche berechnet. Wenn wir das Poisson-Problem lösen, indem wir die Krümmung der Oberfläche am Ausgang gleich der Krümmung der Oberfläche am Eingang setzen (const = 1), ändert sich nichts. Die Stärkung der Gesichtszüge erfolgt, wenn wir einfach die Krümmung erhöhen (const = 2.1). Und wenn const <1 ist, nimmt die Krümmung der resultierenden Oberfläche ab.
Update: ein weiteres Spielzeug als Hausaufgabe
Spielen Sie mit diesem Code herum, um die von
SquareRootOfZero vorgeschlagene Idee zu entwickeln:
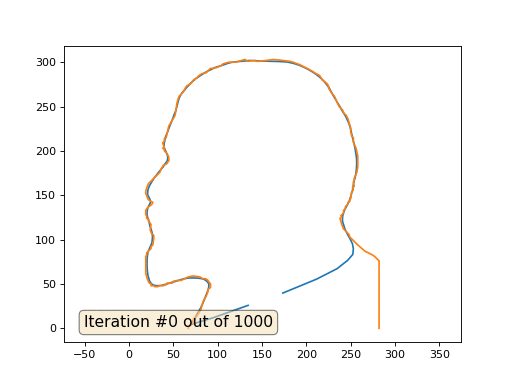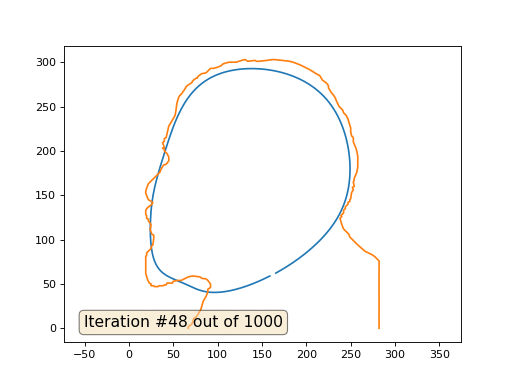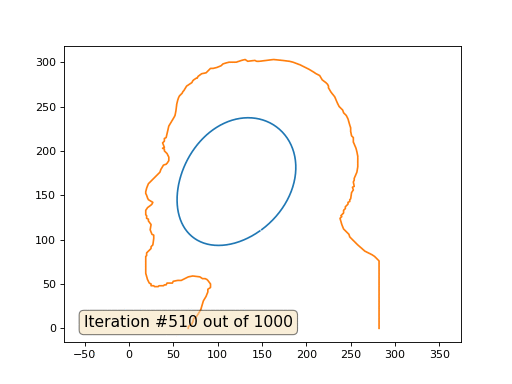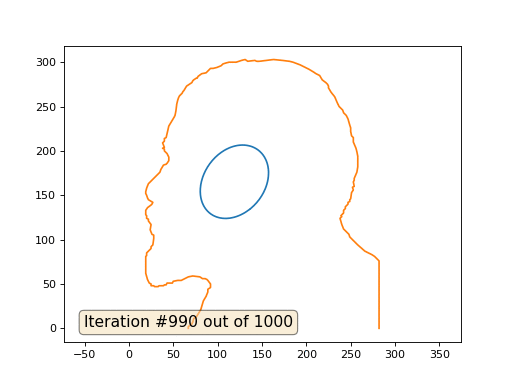
Versteckter Text import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig, ax = plt.subplots() x = [282, 282, 277, 274, 266, 259, 258, 249, 248, 242, 240, 238, 240, 239, 242, 242, 244, 244, 247, 247, 249, 249, 250, 251, 253, 252, 254, 253, 254, 254, 257, 258, 258, 257, 256, 253, 253, 251, 250, 250, 249, 247, 245, 242, 241, 237, 235, 232, 228, 225, 225, 224, 222, 218, 215, 211, 208, 203, 199, 193, 185, 181, 173, 163, 147, 144, 142, 134, 131, 127, 121, 113, 109, 106, 104, 99, 95, 92, 90, 87, 82, 78, 77, 76, 73, 72, 71, 65, 62, 61, 60, 57, 56, 55, 54, 53, 52, 51, 45, 42, 40, 40, 38, 40, 38, 40, 40, 43, 45, 45, 45, 43, 42, 39, 36, 35, 22, 20, 19, 19, 20, 21, 22, 27, 26, 25, 21, 19, 19, 20, 20, 22, 22, 25, 24, 26, 28, 28, 27, 25, 25, 20, 20, 19, 19, 21, 22, 23, 25, 25, 28, 29, 33, 34, 39, 40, 42, 43, 49, 50, 55, 59, 67, 72, 80, 83, 86, 88, 89, 92, 92, 92, 89, 89, 87, 84, 81, 78, 76, 73, 72, 71, 70, 67, 67] y = [0, 76, 81, 83, 87, 93, 94, 103, 106, 112, 117, 124, 126, 127, 130, 133, 135, 137, 140, 142, 143, 145, 146, 153, 156, 159, 160, 165, 167, 169, 176, 182, 194, 199, 203, 210, 215, 217, 222, 226, 229, 236, 240, 243, 246, 250, 254, 261, 266, 271, 273, 275, 277, 280, 285, 287, 289, 292, 294, 297, 300, 301, 302, 303, 301, 301, 302, 301, 303, 302, 300, 300, 299, 298, 296, 294, 293, 293, 291, 288, 287, 284, 282, 282, 280, 279, 277, 273, 268, 267, 265, 262, 260, 257, 253, 245, 240, 238, 228, 215, 214, 211, 209, 204, 203, 202, 200, 197, 193, 191, 189, 186, 185, 184, 179, 176, 163, 158, 154, 152, 150, 147, 145, 142, 140, 139, 136, 133, 128, 127, 124, 123, 121, 117, 111, 106, 105, 101, 94, 92, 90, 85, 82, 81, 62, 55, 53, 51, 50, 48, 48, 47, 47, 48, 48, 49, 49, 51, 51, 53, 54, 54, 58, 59, 58, 56, 56, 55, 54, 50, 48, 46, 44, 41, 36, 31, 21, 16, 13, 11, 7, 5, 4, 2, 0] n = len(x) cx = x[:] cy = y[:] for i in range(0,n): bx = (x[(i-1+n)%n] + x[(i+1)%n] )/2. by = (y[(i-1+n)%n] + y[(i+1)%n] )/2. cx[i] = cx[i] - bx cy[i] = cy[i] - by lines = [ax.plot(x, y)[0], ax.text(0.05, 0.05, "Iteration #0", transform=ax.transAxes, fontsize=14,bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5)), ax.plot(x, y)[0] ] def animate(iteration): global x, y print(iteration) for i in range(0,n): x[i] = (x[(i-1+n)%n]+x[(i+1)%n])/2. + 0.*cx[i]
Dies ist das Standardergebnis, rotes Lenin sind die Anfangsdaten, die blaue Kurve ist ihre Entwicklung, im Unendlichen konvergiert das Ergebnis zu einem Punkt:
Und hier ist das Ergebnis mit dem Koeffizienten 2 .:

Hausaufgaben: Warum verwandelt sich Lenin im zweiten Fall zuerst in Dzerzhinsky und konvergiert dann wieder zu Lenin, aber von größerer Größe?
Fazit
Viele Datenverarbeitungsaufgaben, insbesondere die Geometrie, können als Lösung für ein lineares Gleichungssystem formuliert werden. In diesem Artikel habe ich nicht erklärt,
wie man diese Systeme baut, mein Ziel war nur zu zeigen, dass dies möglich ist. Das Thema des nächsten Artikels lautet nicht mehr "Warum", sondern "Wie" und welche Löser später verwendet werden sollen.
Übrigens und schließlich gibt es im Titel des Artikels die kleinsten Quadrate. Hast du sie im Text gesehen? Wenn nicht, dann ist das absolut nicht beängstigend, das ist genau die Antwort auf die Frage „wie?“. Bleiben Sie auf dem Laufenden, im nächsten Artikel werde ich genau zeigen, wo sie sich verstecken und wie Sie sie ändern können, um Zugriff auf ein äußerst leistungsfähiges Datenverarbeitungstool zu erhalten. In zehn Codezeilen erhalten Sie beispielsweise Folgendes:

Bleib dran für mehr!