Verbesserung der Qualität von Klebepanoramen durch Anpassung des Diagramms projektiver Transformationen

Hallo Habr! Heute werden wir über eine Möglichkeit sprechen, die Qualität von Klebepanoramen zu verbessern. Es gibt einen weit verbreiteten Ansatz zum Kleben von Panoramen flacher Objekte. Da dieser Ansatz jedoch nicht ohne Nachteile ist, bieten wir unsere Verbesserung an.

Die Aufgabe des Schwenkens besteht darin, ein zusammengesetztes Bild basierend auf einem Satz von Quellbildern zu erstellen (siehe 1). Es findet Anwendung bei der Lösung praktischer Probleme wie:

• Ertönen der Erdoberfläche von einem Satelliten oder einer Drohne;
• Zusammenkleben von Bildern, die unter Verwendung eines Mikroskops erhalten wurden;
• Video kleben;
• Superauflösende Bilderfassung.

Abbildung 1 - Originalbilder und Panorama

Im Allgemeinen kann der Panorama-Klebealgorithmus wie folgt formuliert werden [1] (siehe Abb. 2). Zu Beginn ist es erforderlich, eine ausreichende Anzahl von Bildern aus dem Videostream zu extrahieren. Dies kann online erfolgen, indem nacheinander alle Frames gelesen und einzelne Frames mit der erforderlichen Häufigkeit ausgewählt werden.

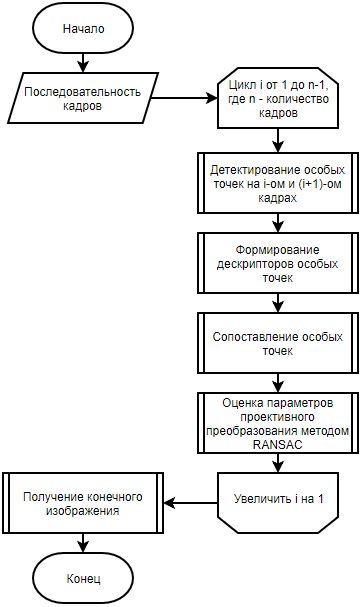
Abbildung 2 - Das Flussdiagramm des Panorama-Klebealgorithmus unter Verwendung spezieller Punkte

Danach müssen nacheinander Bildpaare aus der Menge sortiert werden, um einzelne Punkte zu erkennen und ihre Deskriptoren für diese Bilder zu berechnen [2–4]. Es sind diese singulären Punkte, die es ermöglichen, eine geometrische Entsprechung zwischen zwei Rahmen zu konstruieren. Das Folgende ist ein Vergleich einzelner Punkte basierend auf ihren Deskriptoren. Es ist zu beachten, dass dies die Möglichkeit falscher Übereinstimmungen nicht ausschließt.

Wenn man zwei Sätze von singulären Punkten hat, sollte man eine projektive Transformation finden, die die Punkte eines Rahmens am besten in die entsprechenden Punkte eines anderen umwandelt. Um dieses Problem zu lösen, kann der RANSAC-Ansatz verwendet werden [5]. Dieser Ansatz wird in [6, 7] ausführlicher beschrieben.

Um nach einer projektiven Transformation zwischen Frames zu suchen, kann auch ein optischer Strom verwendet werden, der häufig zum Kleben von Panoramen verwendet wird [8].
Nach Erhalt des erforderlichen Satzes projektiver Transformationen findet ein technisches Verfahren zum Kleben von Bildern statt, nämlich: für jedes Pixel des endgültigen Panoramas (x, y) für jeden Kanal (RGB) den arithmetischen Durchschnitt der Pixelintensitäten mit den Koordinaten (x, y) aller Rahmen einschließlich ein Pixel mit solchen Koordinaten.

Mit den Methoden zur Suche nach projektiven Transformationen kann die Verschiebung der Kameraposition relativ zur vorherigen Position im Raum bestimmt werden. Unter Laborbedingungen reicht die Genauigkeit der Berechnung dieser Daten aus, um ein Panorama eines flachen stationären Objekts zu erstellen. Unter realen Bedingungen tritt bei der Berechnung der Verschiebung der Kameraposition relativ zur vorherigen Position ein Berechnungsfehler auf (Messfehler / Interferenzen / Einschränkungen durch Algorithmen usw.). Mit der Zeit nimmt der akkumulative Fehler weiter zu, so dass das Gesamtpanorama des Objekts trotz der akzeptablen Genauigkeit der Bestimmung der Verschiebung zwischen benachbarten Positionen bereits schwerwiegende Abweichungen enthält (siehe Abb. 3).

Abbildung 3 - Akkumulativer Fehler

Wir haben uns zum Ziel gesetzt, eine Methode zur Anpassung des Diagramms projektiver Transformationen für die Aufgabe des Schwenkens flacher fester Objekte zu entwickeln, die gegen das Problem der Fehlerakkumulation resistent ist. Ein weiteres Ziel ist es, die Methode so zu entwickeln, dass sie nicht von der Methode zur Berechnung der Parameter der projektiven Transformation abhängt.

Eine der Bedingungen muss erfüllt sein:

• Schießen eines stationären pseudostarren Objekts;
• Schießen eines Objekts in der Nähe der Ebene aus einer ausreichend großen Entfernung;
• Für alle Kamerapositionen während der Aufnahme ist die Anforderung erfüllt: Für alle Bildpunkte stimmen die Strahlen, die diese Punkte mit dem Kamerafokus verbinden, nicht miteinander überein.

Beschreibung des Algorithmus zur Anpassung des Projektionstransformationsgraphen

Wir führen das Konzept eines einzelnen Koordinatensystems ein. Mit einem einzelnen Koordinatensystem ist ein Koordinatensystem gemeint, bei dem dieselben Punkte eines Objekts aus verschiedenen Bildern dieselben Koordinaten haben. Diese Anforderung kann durch die folgende Formel ausgedrückt werden:

$$

$$f (x) = y,$$

wo $$$f$ Ist eine Zuordnung für den gemeinsamen Teil der Frames definiert und übersetzt die Punkte des ersten Frames in die Punkte des zweiten Frames? $$$x$ - Koordinaten des Punktes im Koordinatensystem des ersten Rahmens, $$$y$ - Koordinaten eines Punktes im Koordinatensystem des zweiten Rahmens.

Im Falle der Zuordnung $$$f$ kann korrekt über den Schnittpunkt von Frames hinaus fortgesetzt werden, können wir den zweiten Frame mit Informationen aus dem ersten ergänzen. Somit wird eine Karte erhalten, die als Mosaik aus zwei oder mehr Rahmen zusammengeklebt ist.

Nachdem die projektiven Transformationen zwischen benachbarten Frames gefunden wurden, erfolgt eine anfängliche Verklebung, mit der die eindeutige Position der Frames in einem einzelnen Koordinatensystem festgelegt wird (siehe Abb. 4).

Abbildung 4 - Die eindeutige Position des Rahmens auf der Karte

Nach dem Erstellen des primären Klebens von Bildern wird ein Diagramm projektiver Transformationen erstellt $$$G$ ::

$$

$$G = (V, E),$$

wo $$$V$ - viele vier Punkte, die die Eckpunkte projektiv korrigierter Bilder sind; $$$\ vert V \ vert = n$ , $$$E$ - viele projektive Transformationen zwischen Frames; $$$\ vert E \ vert = m$ .

Eine Kante zwischen den Eckpunkten wird nur konstruiert, wenn sich die Rahmen mindestens bei schneiden $$$T \%$ zum Primärkleben (IoU - Intersection over Union) (siehe Abb. 5, 6):

$$

$$\ frac {s_ {ij}} {s_i + s_j-s_ {ij}} \ cdot100 \%> T \%.$$

Abbildung 5 - Rahmenschnittpunkt

Schwelle $$$T$ Sie wird abhängig von der Methode ausgewählt, mit der nach einer projektiven Transformation gesucht wird, indem zwischen der Konditionalität der Aufgabe der Suche nach einer projektiven Transformation zwischen zwei Frames und der gewünschten erwarteten Anzahl von Kanten und Zyklen im Diagramm abgewogen wird.

Abbildung 6 - Ein Beispiel für die Diagrammkonstruktion

Als Ergebnis der Graph der projektiven Transformationen $$$G$ sieht wie folgt aus (siehe Abb. 7):

Abbildung 7 - Das endgültige Diagramm der projektiven Transformationen

Wenn das Diagramm Zyklen enthält (siehe Abb. 6), werden darin redundante Informationen angezeigt, die auch Widersprüche enthalten können. Um festzustellen, welche Art von Widersprüchen auftreten können, betrachten wir einen bestimmten Zyklus des Diagramms (siehe Abb. 8). Lassen Sie diesen Zyklus aus Eckpunkten bestehen $$$1,2, ..., k$ . Dann haben wir eine Reihe von projektiven Abbildungen entlang dieses Zyklus:

$$

$$H_ {12}: 1 \ to2, \\ H_ {23}: 2 \ to3, \\ ... \\ H_ {k1}: k \ to1. \\ $$

Betrachten Sie die Zusammensetzung dieser Zuordnungen:

$$

$$H_ {k1} * ... * H_ {23} * H_ {12} = H_ {11}.$$

Abbildung 8 - Grafikschleife

Anzeige $$$H_ {11}$ muss eine identische Zuordnung sein. Wenn die Zuordnung $$$H_ {11}$ anders als identisch, dann sagen wir, dass ein Widerspruch erhalten wird. In diesem Fall wird der Zyklus als inkonsistent bezeichnet . Somit gibt es ein Problem, das mit dem Vorhandensein inkonsistenter Zyklen im Diagramm projektiver Abbildungen verbunden ist, da bei perfekter Verklebung die Widersprüche im Diagramm projektiver Transformationen $$$G$ muss abwesend sein.

Wir beschreiben den Anpassungsalgorithmus für den Graphen projektiver Transformationen, d. H. Die Anpassung aller seiner Zyklen. Um den akkumulativen Fehler zu minimieren, der auftritt, wenn der Zyklus im Diagramm der projektiven Transformationen geschlossen wird, wird das Konzept der SLAM-Methode (Simultaneous Localization And Mapping) verwendet [9].

Betrachten Sie in jedem Rahmen vier Punkte in der allgemeinen Position. Lassen Sie die Frames von nummerieren $$$1$ vorher $$$n$ dann werden vier Punkte mit bezeichnet $$$p_i$ wo $$$1 \ le i \ le n$ . Solch ein Satz von vier Punkten $$$P$ Definiert ein einzelnes Koordinatensystem eindeutig, da Sie für zwei beliebige Frames eindeutig eine projektive Karte finden können, die vier Punkte in einen anderen übersetzt.

Um die Menge von vier Punkten zu finden, die den gewünschten konsistenten Graphen bestimmen, können Sie die Methode der kleinsten Quadrate verwenden. Wir minimieren die Funktion, die gleich der Summe über alle Kanten der Menge ist $$$E$ zählen $$$G$ und für jede Kante - die Summe von vier Mengenpunkten $$$\ Vert H_ {ij} p_ {is} -p_ {js} \ Vert$ . Um eine Lösung zu finden, die die Funktion minimiert, wird vorgeschlagen, die konjugierte Gradientenmethode zu verwenden.

$$

$$\ sum _ {(i, j) \ in E} \ sum_ {s = 1} ^ 4 \ Vert H_ {ij} p_ {is} -p_ {js} \ Vert \ to \ min_ {P}.$$

Nachdem für jeden Frame eine projektive Transformation durchgeführt wurde, mit der die Position des Frames auf der Karte eindeutig festgelegt wird, können Sie ein Panoramabild erhalten.

Experimentelle Ergebnisse

Bisher gibt es keine universelle Methode zur Beurteilung der Qualität von Klebebildern. In der Regel wird die Qualität des Klebens von Experten organoleptisch bewertet. Für die wissenschaftliche Forschung ist jedoch eine quantitative, automatisch berechnete Qualitätsbewertung vorzuziehen.

Um die Qualität des Klebens ohne die Teilnahme eines menschlichen Experten beurteilen zu können, ist ein Standardkleben erforderlich, mit dem das Ergebnis verglichen wird. Der Ansatz, bei dem das Kleben aus einem realen Video erhalten wurde und das Foto des gesamten Objekts als Standardkleben betrachtet wird, erfordert gute Laborbedingungen unter Verwendung eines Manipulators, der in der Lage ist, die Position der Kamera im Raum physikalisch (unter Verwendung von Sensoren) zu fixieren. Diese Qualitätsbewertungsmethode ist jedoch kostspielig.

Um die Qualität der Panoramaklebung mit einem hochauflösenden Bild zu quantifizieren, schlagen sie in [10] vor, ein künstliches Video zu erstellen, dessen Bilder projektiv verzerrte Bereiche des Originalbilds sind (siehe Abb. 9). Projektiv verzerrte alle Frames mit Ausnahme des ersten, da ein einzelnes Koordinatensystem relativ zum ersten Frame angegeben ist. Ferner werden diese Bilder von künstlichem Video in ein Panorama eingeklebt, das weiter mit dem ursprünglichen Referenzbild verglichen wird. Mit diesem Ansatz ist es möglich, die Probleme des Helligkeitsunterschieds der erhaltenen und der Referenzklebstoffe sowie der Verzerrung der Szene zu vermeiden.

Abbildung 9 - Originalbild und Einzelbild eines künstlichen Videos

Um die Qualität des Klebens vor und nach der Vereinbarung eines Diagramms zu vergleichen, wurde eine Testprobe von 50 Bildern erstellt und 50 künstliche Videos aus den Originalbildern erstellt, nach denen das Kleben durchgeführt wurde (siehe 10). Alle erhaltenen Panoramen wurden auf die Größe der Quellbilder reduziert, und für jedes Panorama wurde das Fehlermaß berechnet:

$$

$$RMSE = \ sqrt {\ frac {\ sum_ {i = 1} ^ h \ sum_ {j = 1} ^ w ((I_ {ij} ^ R- \ hat {I_ {ij} ^ R}) ^ 2+ (I_ {ij} ^ G- \ hat {I_ {ij} ^ G}) ^ 2+ (I_ {ij} ^ B- \ hat {I_ {ij} ^ B}) ^ 2)} {h \ cdot w \ cdot 3}},$$

wo $$$h$ - Bildhöhe $$$w$ - Bildbreite $$$I_ {ij} ^ R$ - Pixelintensität $$$(i, j)$ das resultierende Panorama auf dem roten Kanal ( $$$G$ - grüner Kanal $$$B$ - blauer Kanal) $$$\ hat {I_ {ij} ^ R}$ - Pixelintensität $$$(i, j)$ Quellbild auf dem roten Kanal ( $$$G$ - grüner Kanal $$$B$ - blauer Kanal).

Abbildung 10 - Panorama vor der Übereinstimmung des Diagramms (RMSE = 35,3) und danach (RMSE = 14,2)

In der grafischen Darstellung sieht der RMSE auf dem Testsatz wie folgt aus (siehe Abb. 11):

Abbildung 11 - RMSE an der Testprobe. Frames werden in aufsteigender Reihenfolge von RMSE sortiert, bis der Graph übereinstimmt.

In Übereinstimmung mit jedem Wurzelwert des quadratischen Mittelwertfehlers vor dem Abgleich werden die Wurzelwerte des quadratischen Mittelwertfehlers nach dem Abgleich des Diagramms dargestellt. Der mittlere RMSE-Wert für die Testprobe vor der Konsistenz des Diagramms beträgt 35,5 , nachdem das Diagramm übereinstimmt - 13,9 .

Fazit

Basierend auf den Ergebnissen des Vergleichs der Qualität des Klebens können wir den Schluss ziehen, dass das Anpassen des Diagramms den akkumulierten Fehler erheblich reduziert und die Qualität der Klebepanoramen verbessert. Es sollte jedoch berücksichtigt werden, dass der Graphabgleich nur dann hilfreich sein kann, wenn der Graph projektive Transformationen Zyklen enthält. Wenn im Diagramm der projektiven Transformationen keine Zyklen vorhanden sind, beeinträchtigt das Diagrammanpassungsmodul die Qualität der Panoramaklebung nicht.

Es ist erwähnenswert, dass diese Methode des Graph Matching mit einer Reihe von projektiven Transformationen funktioniert und die Art und Weise, wie diese projektiven Transformationen gefunden wurden, für diese Methode keine Rolle spielt.

In Zukunft ist geplant, die Komplexität des Algorithmus zu optimieren, da er nur für "Offline" -Benutzerfälle gilt.

Literatur

[1] Gubin A.Yu., Kovin R.V. Ein einfacher Ansatz für die Aufgabe, überlappende Bilder in ein Panorama zu kleben // X Internationale wissenschaftliche und praktische Konferenz von Studenten, Doktoranden und jungen Wissenschaftlern "Jugend und moderne Informationstechnologien", p. 79-81, 2012.
[2] Drummond T., Rosten E. Maschinelles Lernen für die schnelle Kurvenerkennung // 9. Europäische Konferenz für Computer Vision (ECCV), S. 1. 430-443, 2006.
[3] Unterscheidungsmerkmale von Lowe DG anhand von skalierungsinvarianten Schlüsselpunkten // International Journal of Computer Vision, S. 22. 91-110, 2004.
[4] Bay H., Ess A., Yuitelaars T., Van Gool L. SURF: Beschleunigte robuste Funktionen // Computer Vision und Bildverständnis, v. 110, p. 346-359, 2008.
[5] Martin A. Fischler, Robert C. Bolles. Zufallsstichprobenkonsens: Ein Paradigma für die Modellanpassung mit Anwendungen zur Bildanalyse und automatisierten Kartografie // Comm. der ACM, v. 24, p. 381-395, 1981.
[6] Arlazarov V.L., Bulatov K.B., Chernov T.S. Die Methode der Fuzzy-Bildsuche in großen Mengen von Videodaten // High Availability Systems, Vol. 12, No. 1, p. 53-58, 2016.
[7] Skoryukina N. et al. Snapscreen: TV-Stream-Frame-Suche mit projektiv verzerrter und verrauschter Abfrage // 9. Internationale Konferenz über Bildverarbeitung (ICMV) - Proc. SPIE V. 10341, S. 103410Y, 2017.
[8] Bouguet JY Pyramidale Implementierung des Affine Lucas Kanade Feature Trackers: Beschreibung des Algorithmus // Intel Corporation, V. 5, p. 1-10, 2001.
[9] Newman P., Ho K. Schließen der SLAM-Schleife mit visuell herausragenden Merkmalen // IEEE Proc. der Internationalen Konferenz für Robotik und Automatisierung, p. 635-642, 2005.
[10] Paalanen P., Kamarainen JK, Kalviainen H. Bildbasierte quantitative Mosaikbewertung mit künstlichem Video // Skandinavische Konferenz zur Bildanalyse, Springer (Berlin, Heidelberg), p. 470-479, 2009.