Wellenprozesse in Hydraulikleitungen. Die Grundlagen

Hallo Habr!

In einem früheren Artikel habe ich über die Methode der Eigenschaften gesprochen, mit der Wellenprozesse in Hydraulikleitungen berechnet werden können. In der Tat können Wellenprozesse natürlich im Kopf berechnet werden, Sie müssen nur den Ansatz kennen.

Unter dem Schnitt zeige ich "an den Fingern" und mit Hilfe von Gifs die Hauptwelleneffekte. Als Beispiel werde ich wieder die Hydraulikleitung verwenden, aber tatsächlich basieren sie auf fast den gleichen Gleichungen wie für akustische und elektrische Leitungen. Selbst wenn Sie keine Hydraulik sind, kann es einfache Analogien geben, die Ihnen helfen, Wellenprozesse im Allgemeinen zu verstehen.

Achtung Unter der Katze 15 MB animierte Gifs!

Hier betrachten wir also die Ausbreitung eindimensionaler ebener Wellen in einer Hydraulikleitung. Diese Annahme gilt durchaus für lange Rohrleitungen, deren Länge um ein Vielfaches größer ist als der Innendurchmesser. Der Einfachheit halber vernachlässigen wir vorerst auch die Reibung. In diesem Fall werden die laufenden physikalischen Prozesse durch ein Paar partieller Differentialgleichungen beschrieben:

$$

$$\ frac {\ partielles p} {\ partielles t} + \ rho \; c ^ 2 \ frac {\ partielles v} {\ partielles x} = 0$$

$$

$$\ frac {\ partielle v} {\ partielle t} + \ frac1 \ rho \ frac {\ displaystyle \ partielle p} {\ displaystyle \ partielle x} = 0$$

wo $$$\ rho$- Dichte $$$v$- Geschwindigkeit $$$p$- Druck $$$c$- Schallgeschwindigkeit.

Aus Gewohnheit kann das Aussehen dieser Gleichungen erschrecken, aber tatsächlich ist hier alles einfach. Die erste Gleichung besagt, dass der Druck mit der Zeit zunimmt, wenn mehr Flüssigkeit in das Rohrsegment fließt als herausfließt (außerdem ist die Flüssigkeit im Rohr umso dichter und elastischer, je schneller sie ist). Die zweite Gleichung zeigt, dass zum Beschleunigen eines Segments einer Flüssigkeit eine Druckdifferenz angelegt werden muss (je größer die Dichte, desto mehr Druckdifferenz muss angewendet werden, um das Segment zu beschleunigen). Das heißt, Es werden ganz banale Dinge beschrieben: Die Flüssigkeit ist komprimierbar, die Flüssigkeit hat eine Masse.
Lassen wir die analytische Lösung dieser Gleichungen für zukünftige Artikel und gehen wir sofort zum Beispiel „an den Fingern“ über.
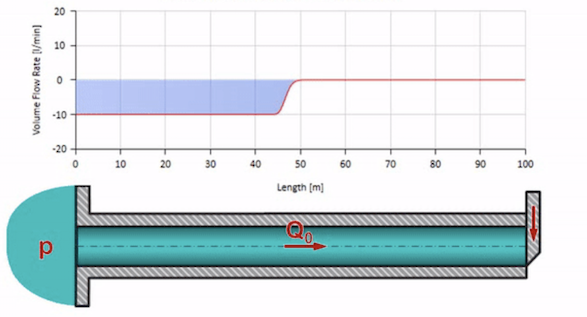
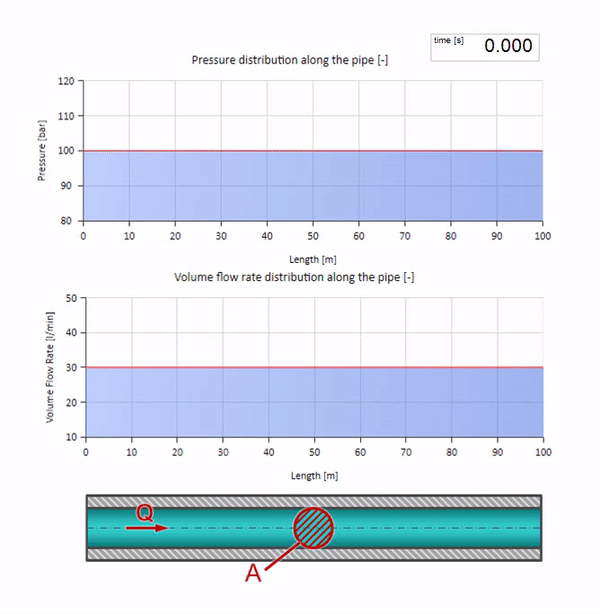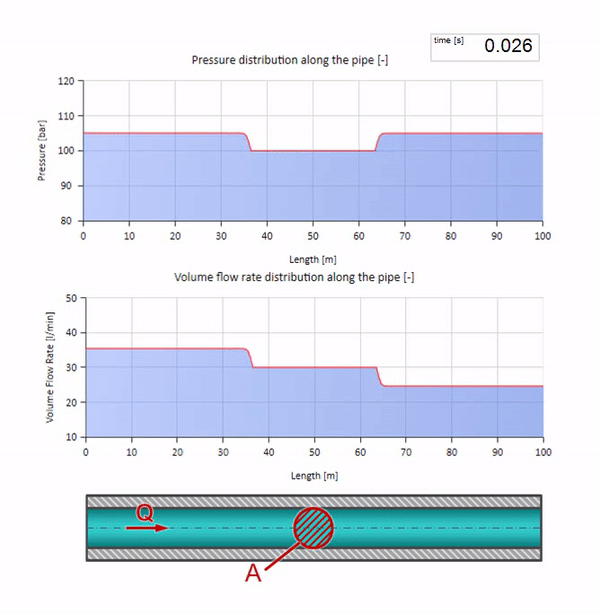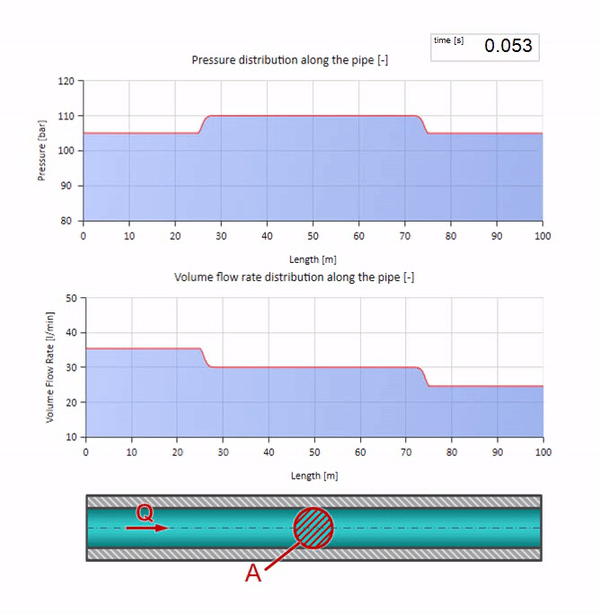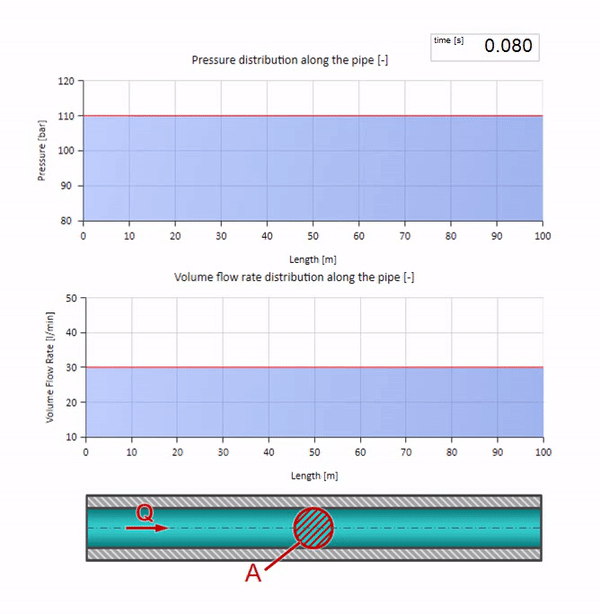
Nehmen Sie ein mit Wasser gefülltes Rohr, in dem ein Druck von 100 bar (10 MPa) aufrechterhalten wird und eine Durchflussrate von 30 l / min fließt. Wenn am linken Ende ein Druckschritt angewendet wird, beginnt er sich vorhersehbar mit einer Geschwindigkeit entlang des Stroms zu bewegen, die der Schallgeschwindigkeit im Medium entspricht.

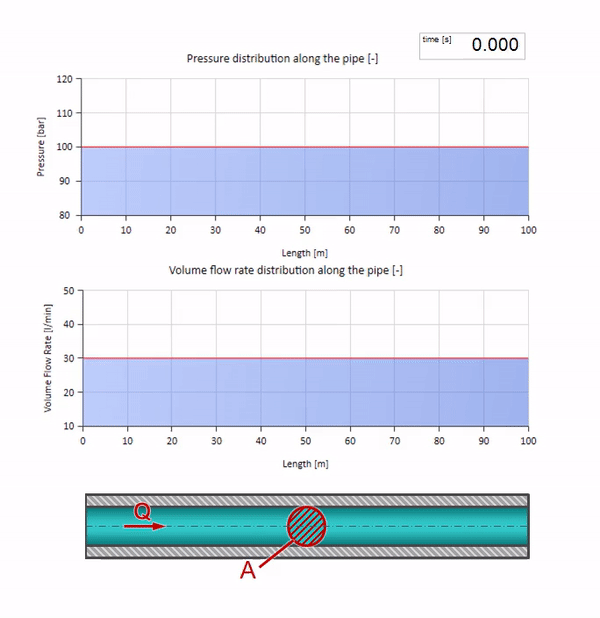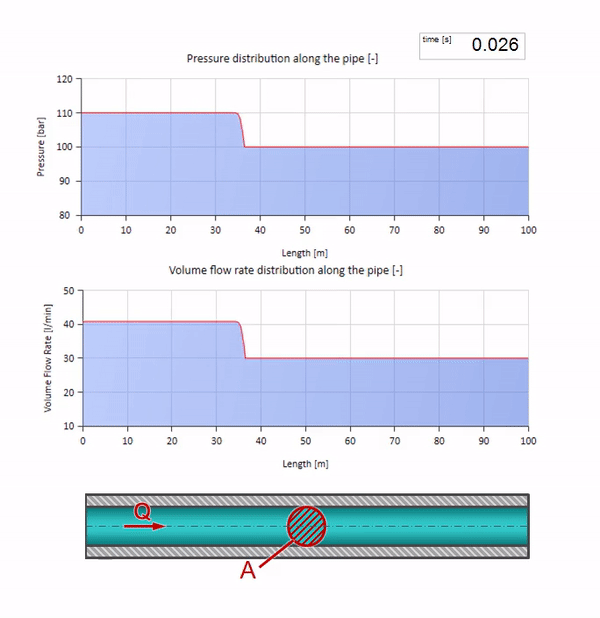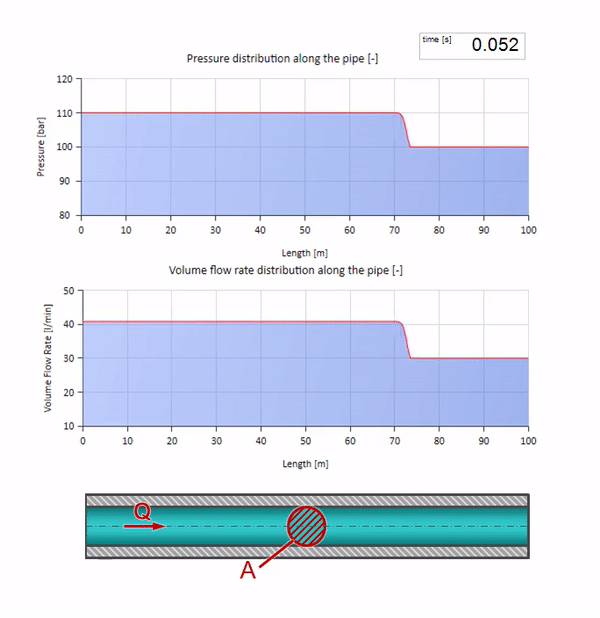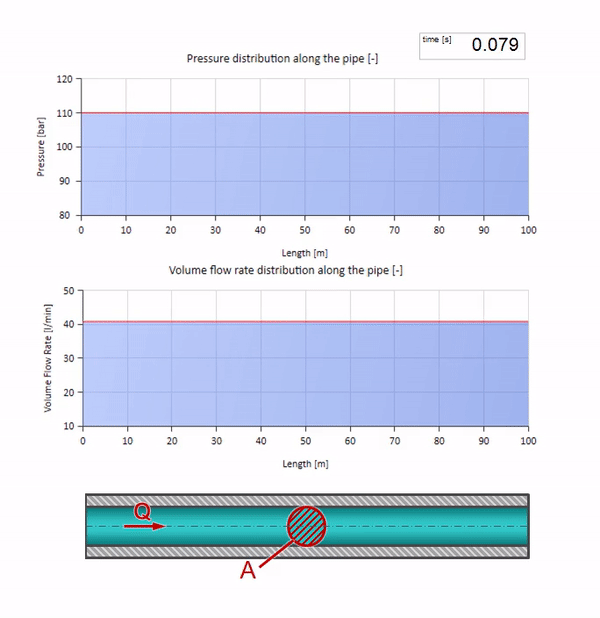
Mit dem Druck ändert sich natürlich auch die Durchflussmenge. Wenn der Druck ansteigt, wird die Flüssigkeit stromaufwärts „eingestellt“ und die Durchflussrate ebenfalls um einen „Schritt“ erhöht. Wie viel wird durch den Wert der Wellenimpedanz bestimmt. Für ein Rohr mit Querschnittsfläche $$$A$gefüllt mit Flüssigkeit mit Dichte $$$\ rho$und lokale Schallgeschwindigkeit $$$c$Die Wellenimpedanz kann wie folgt berechnet werden:

$$

$$Z_L = \ frac {\ rho \; c} A$$

In Bezug auf die Abmessungen entspricht dies dem herkömmlichen hydraulischen Widerstand, der nur zur Berechnung der Druckwellenverhältnisse verwendet wird ( $$$\ widehat p$) und Durchflussrate ( $$$\ widehat Q$) und nicht ihre absoluten Werte:

$$

$$Z_L = \ frac {\ widehat p} {\ widehat Q}$$

Je größer die Dichte und Geschwindigkeit des Schalls ist, desto höher ist die Wellenimpedanz, d.h. Je schwieriger es für einen bestimmten Druckabfall ist, die Flüssigkeit zu dispergieren (Durchfluss erhöhen)

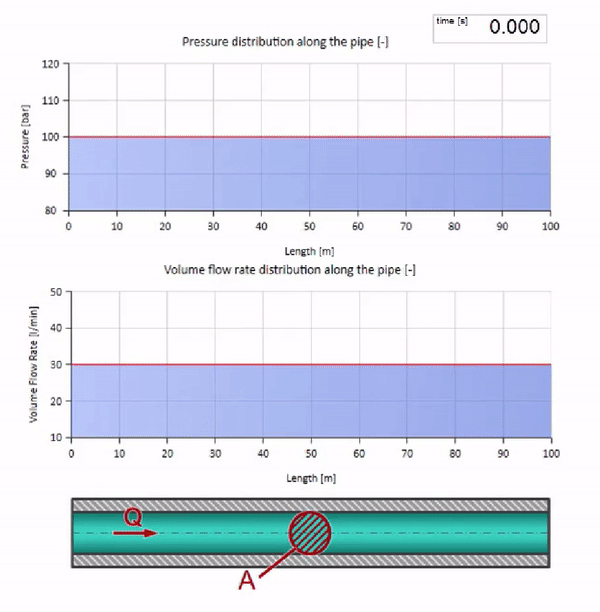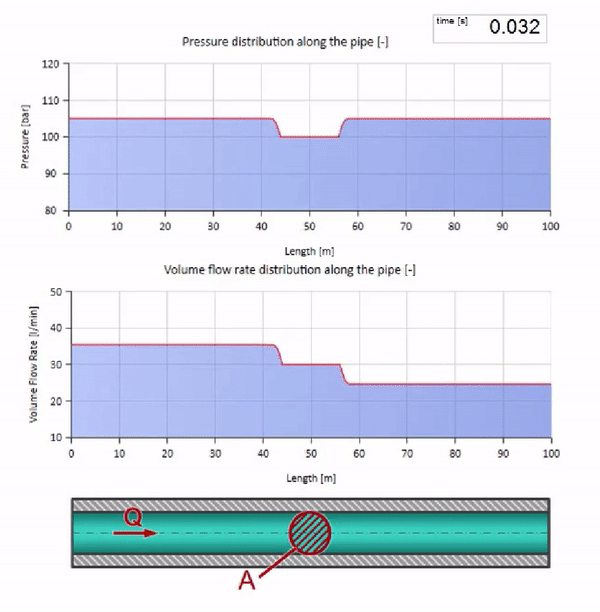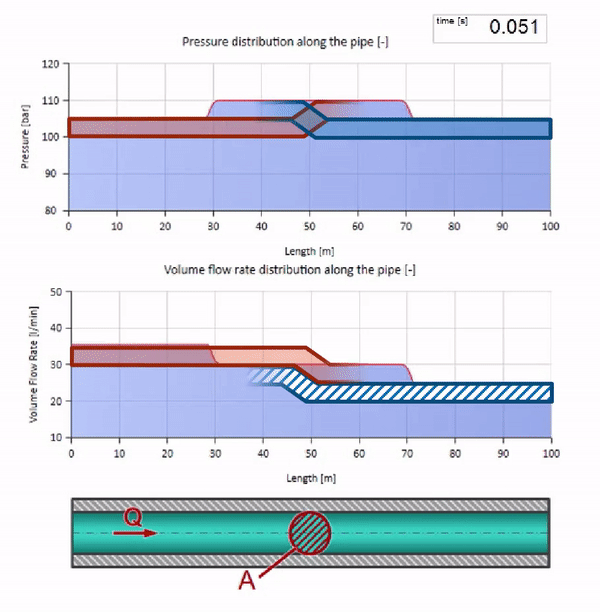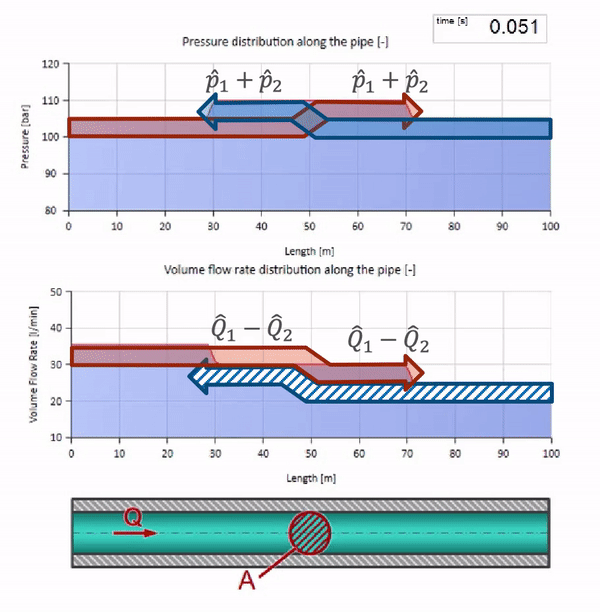
Nun wollen wir sehen, wie sich zwei Wellen aufeinander zu bewegen:

Wenn der Druck am rechten Ende ansteigt, wird die Flüssigkeit unweigerlich durch ein negatives Differential gehemmt. Dies bedeutet, dass die gegen die Strömung gerichtete Druckanstiegswelle zu einer Abnahme der Strömungsrate um einen Betrag führt, der wiederum durch den Wellenwiderstand bestimmt wird. Das heißt, eine Welle des Druckwachstums und des fallenden Flusses bewegt sich nach rechts.
Bei einer Kollision scheint es, dass die Strömungswellen voneinander reflektiert werden und zurückgehen. Tatsächlich überlappen sie sich einfach. Dieser Effekt wird auch als Interferenz bezeichnet:

Jetzt wissen wir, dass jedes Rohr mit einer Flüssigkeit eine Eigenschaft wie den Wellenwiderstand hat. Es ist interessant zu sehen, was mit der Welle passiert, wenn sich der Durchmesser eines Rohrs in einem bestimmten Abschnitt dramatisch ändert:

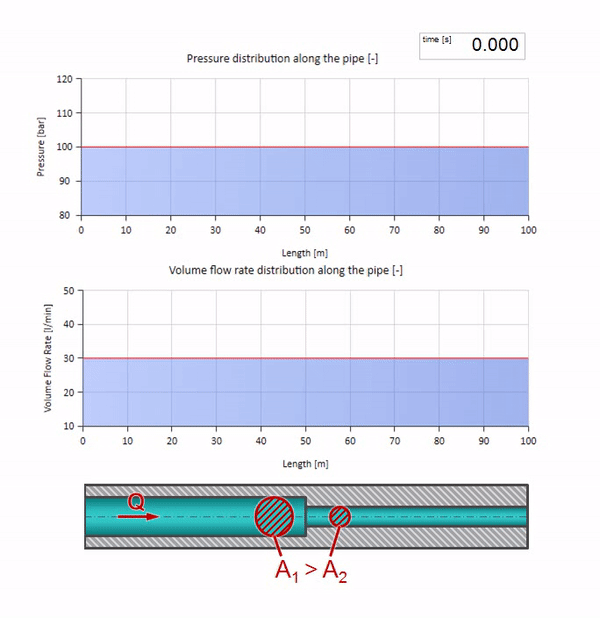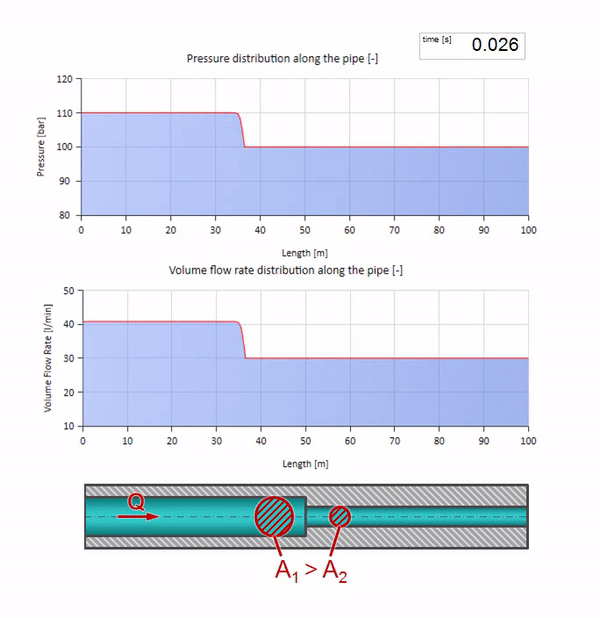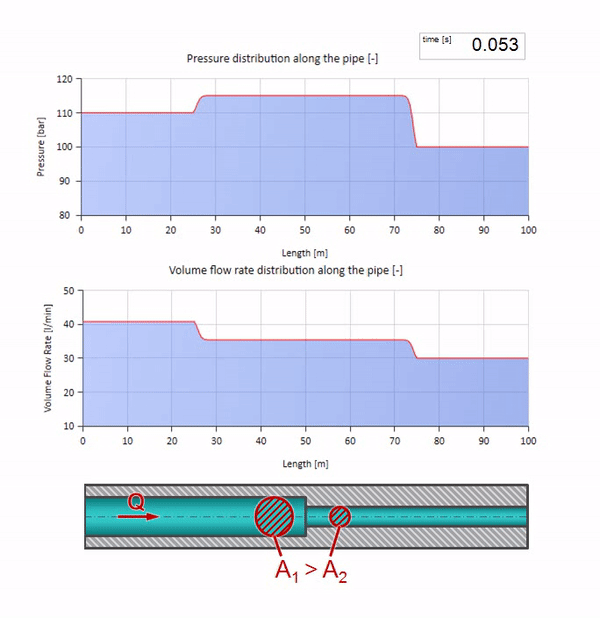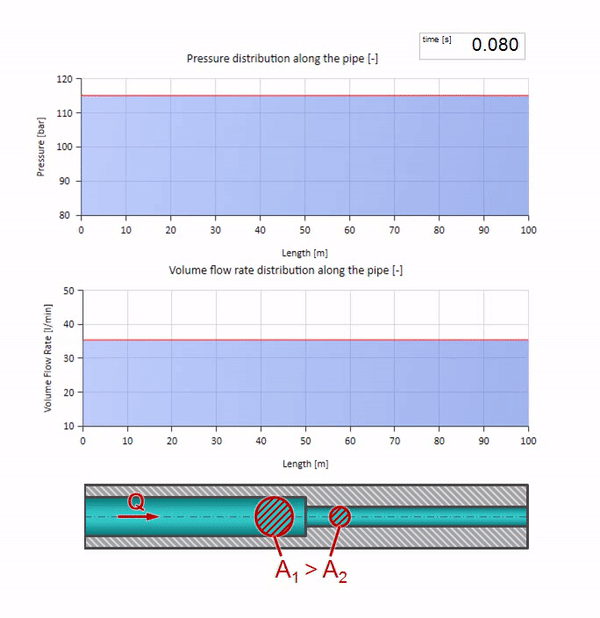
Bevor die Welle einen Ort mit einer Verringerung des Rohrdurchmessers erreicht, passiert natürlich nichts Interessantes. Dann erreicht es jedoch einen Abschnitt mit einem höheren Wellenwiderstand, was bedeutet, dass das Verhältnis der Druckwelle zur Strömungswelle größer sein sollte als im linken Rohrabschnitt. Dies bedeutet, dass die Druckwelle zunehmen und die Durchflussrate abnehmen sollte. Gleichzeitig bleibt der Welle nichts anderes übrig, als sich nach links zu biegen, während an der Verbindungsstelle der beiden Rohre gleiche Werte beibehalten werden.

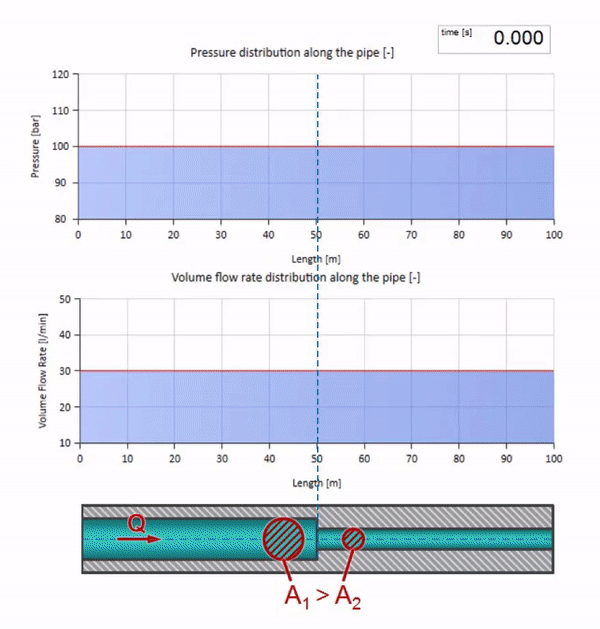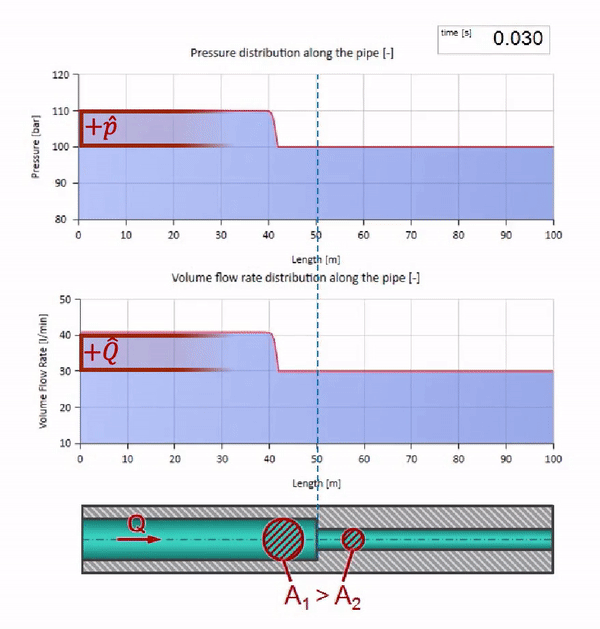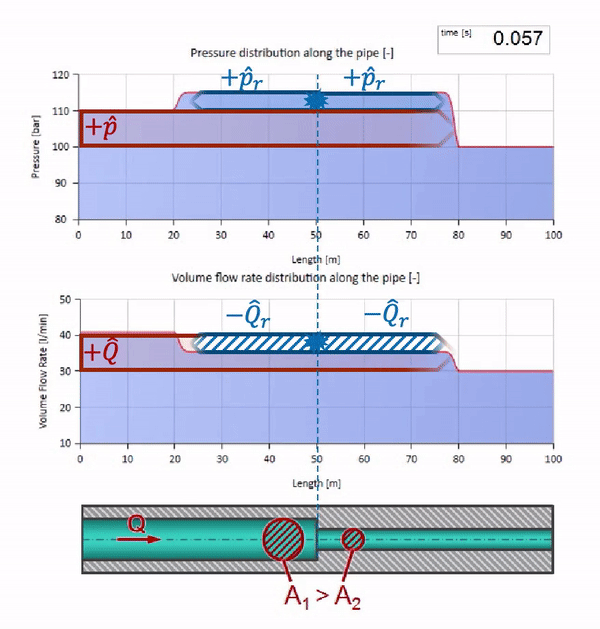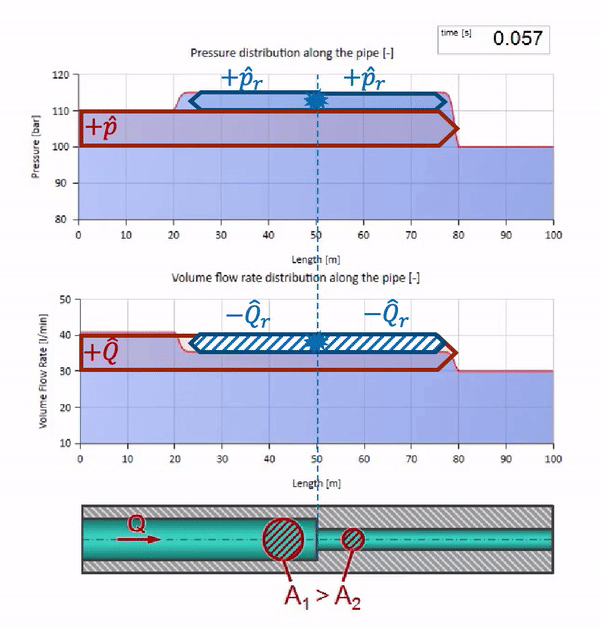
Für Berechnungen ist es zweckmäßig, den Reflexionskoeffizienten zu verwenden $$$r$, was aus den Wellenimpedanzen einzelner Abschnitte hervorgeht:

$$

$$r = \ frac {Z_2-Z_1} {Z_1 + Z_2}$$

Dann können die reflektierten Druck- und Strömungswellen wie folgt berechnet werden:

$$

$${\ widehat p} _r = r \; \ widehat p$$

$$

$${\ widehat Q} _r = - \ frac {\ displaystyle \; {\ widehat p} _r} {Z_1} = - r \; \ widehat Q$$

und diese Wellen selbst werden nach dem Gesetz der Interferenz mit der ursprünglichen überlagert.
Und es sieht aus wie ein Bild der Reflexion einer Welle von einem Ort mit einem niedrigeren Wellenwiderstand:

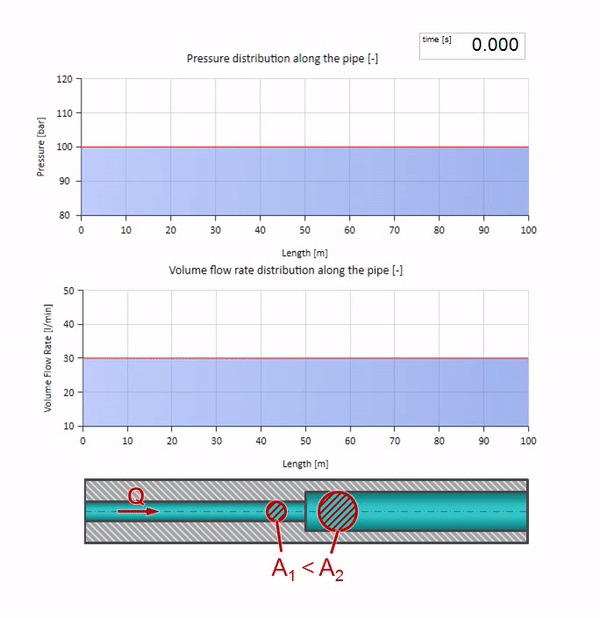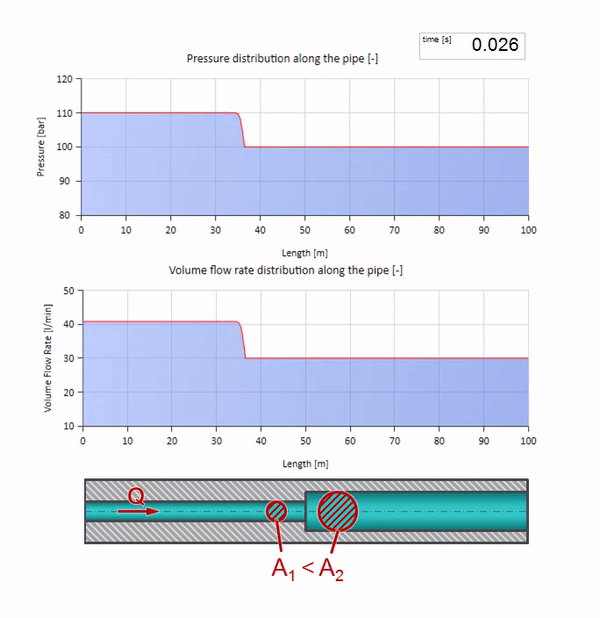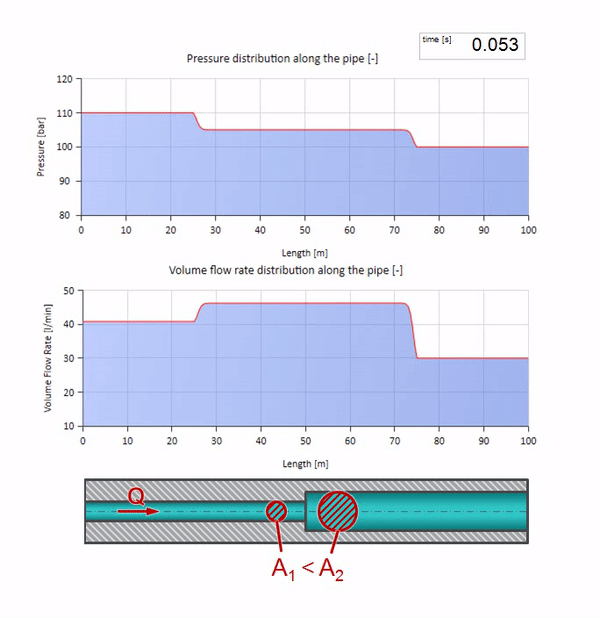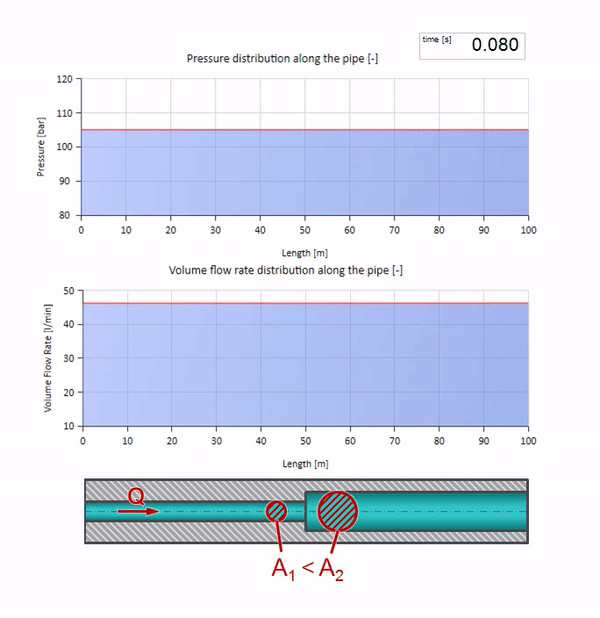
Es ist ersichtlich, dass diesmal der Reflexionskoeffizient negativ ist, was bedeutet, dass die Druckwelle nach der Reflexion geringer und die Durchflussrate im Gegenteil größer ist.

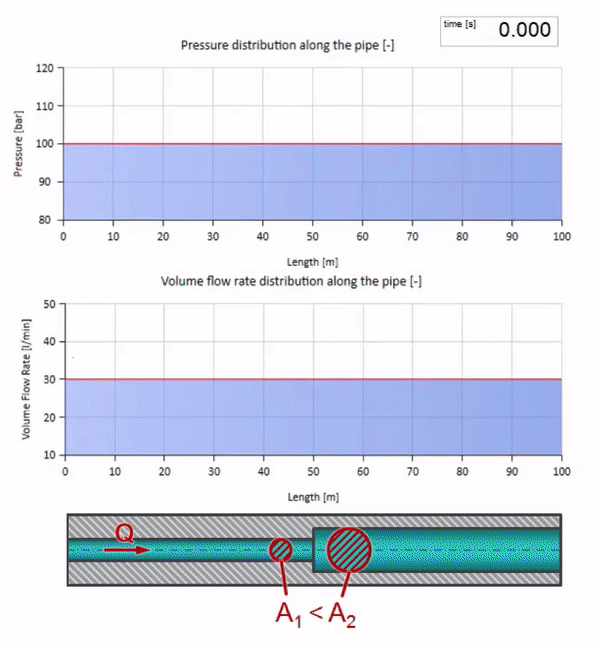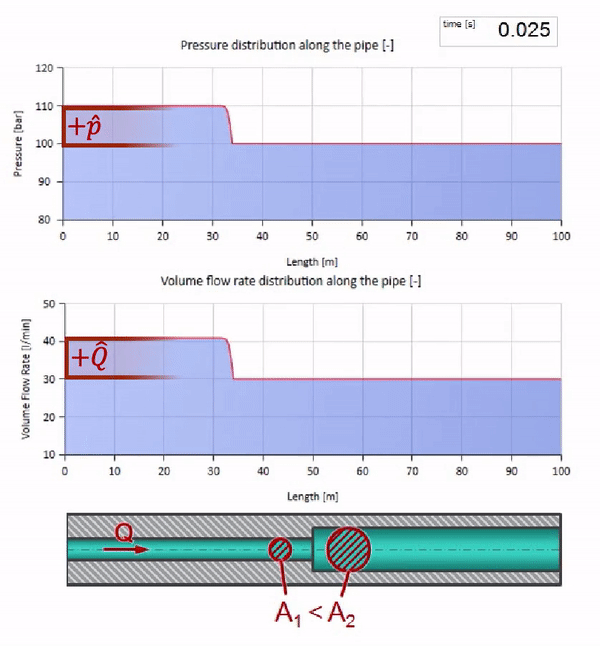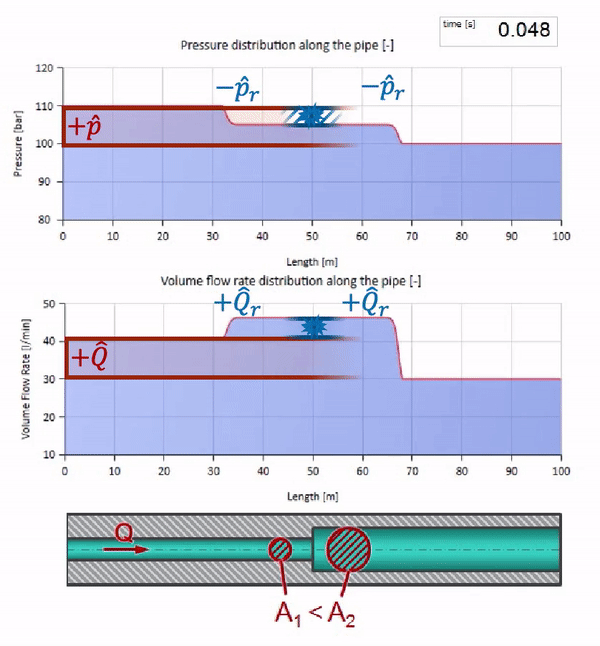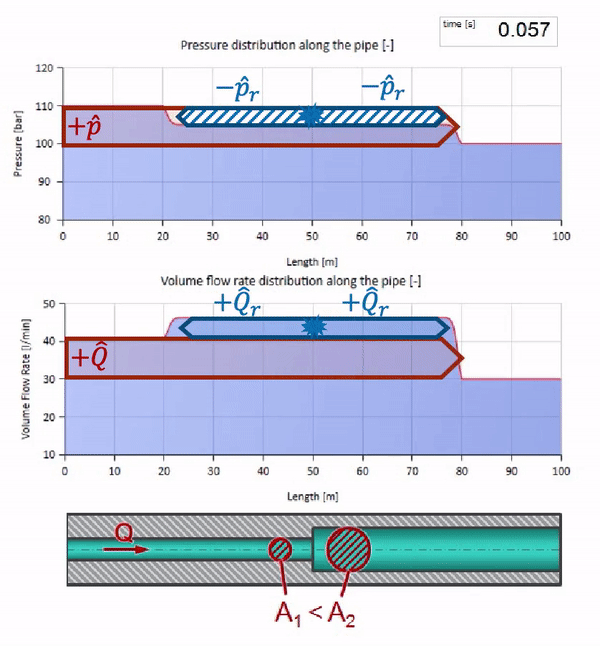
Es ist zu beachten, dass die Impedanz nicht nur von der Größe des Rohrs, sondern auch von der lokalen Schallgeschwindigkeit abhängt. Das heißt, Wenn wir einen Rohrabschnitt mit einer Gummimanschette haben, in der die Schallgeschwindigkeit viel niedriger ist, wird die Welle auch reflektiert:

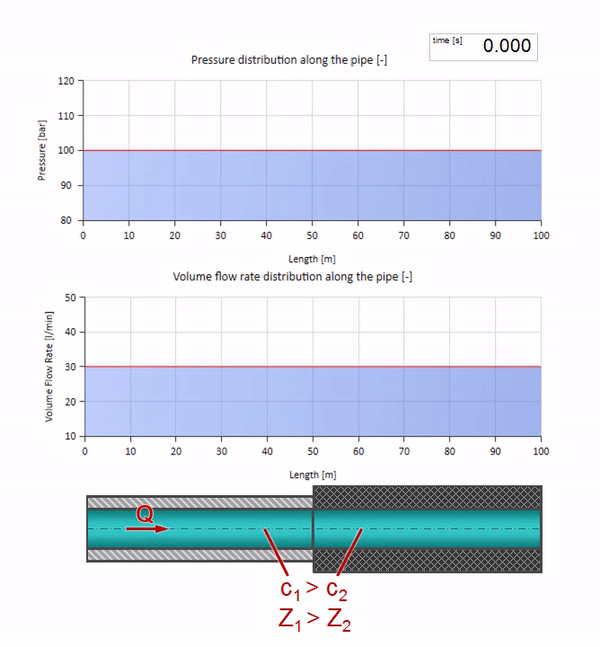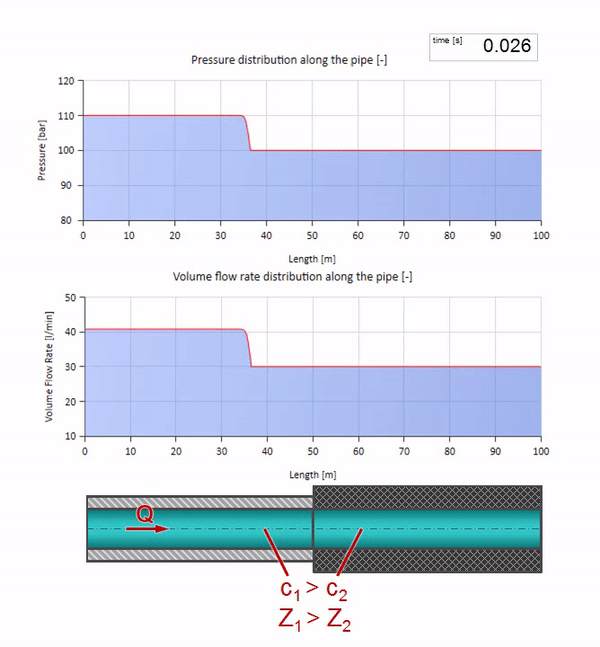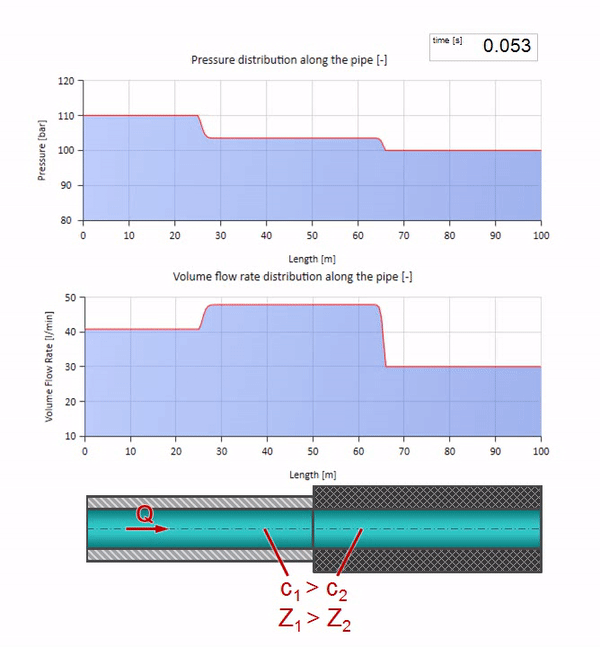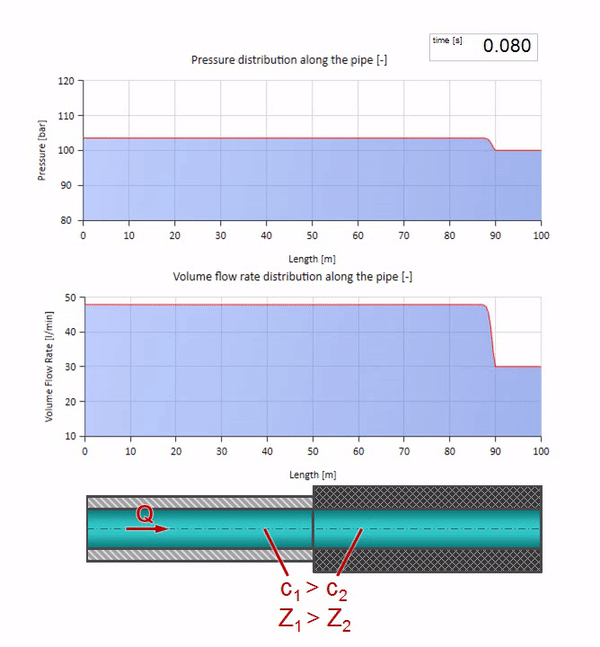
Erstens fällt sofort auf, dass sich die Welle im Abschnitt mit der Gummiwand des Rohrs langsamer bewegt. Und da der Wellenwiderstand geringer ist, ähnelt das Ergebnis der Reflexion dem Fall mit der Ausdehnung des Rohrs:

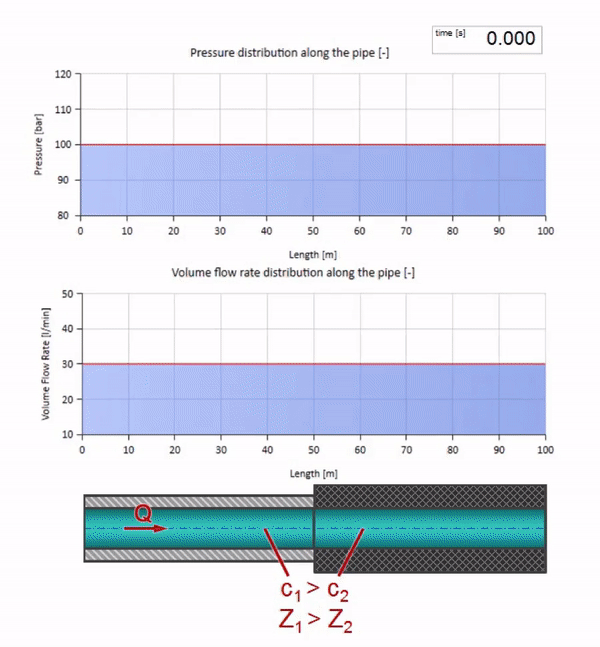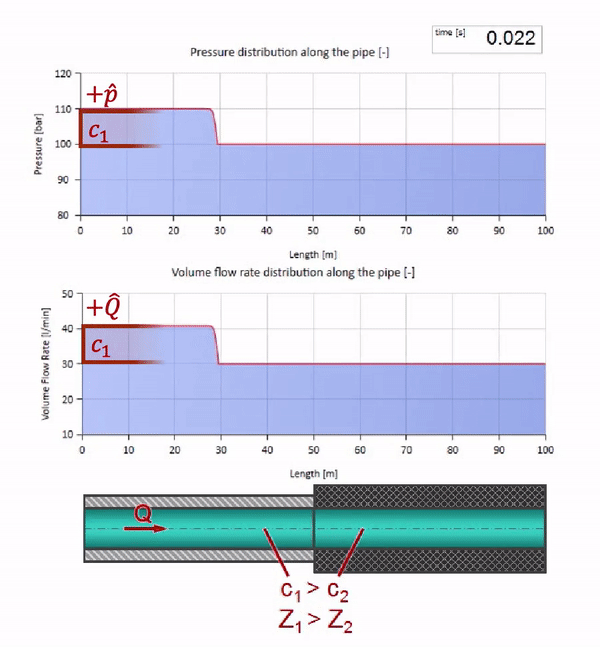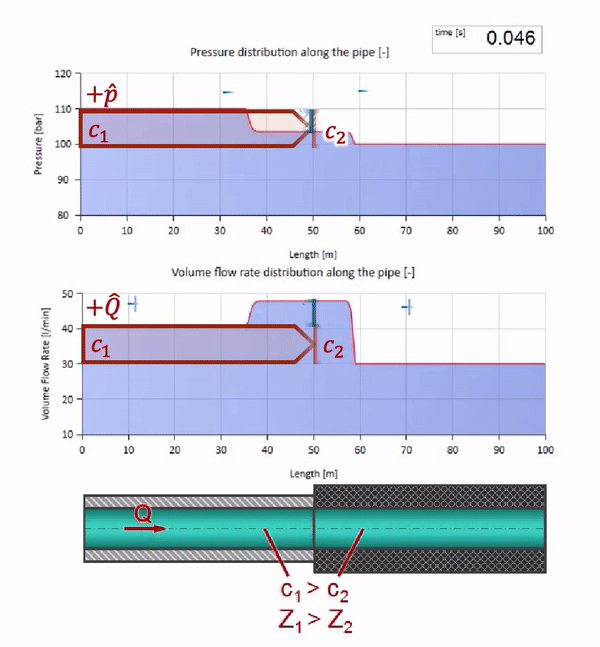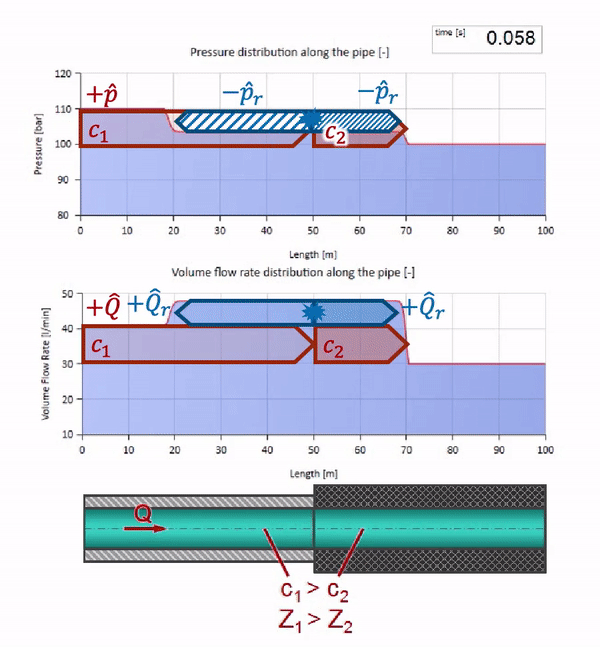
Nun wäre es schön, Extremfälle mit null und unendlich großen Werten der Wellenimpedanz zu betrachten. Dies ist der Auslass der Rohrleitung in den Tank mit konstantem Druck bzw. das geschlossene Ende. Ich werde diese Animationen ohne Kommentar hinterlassen:


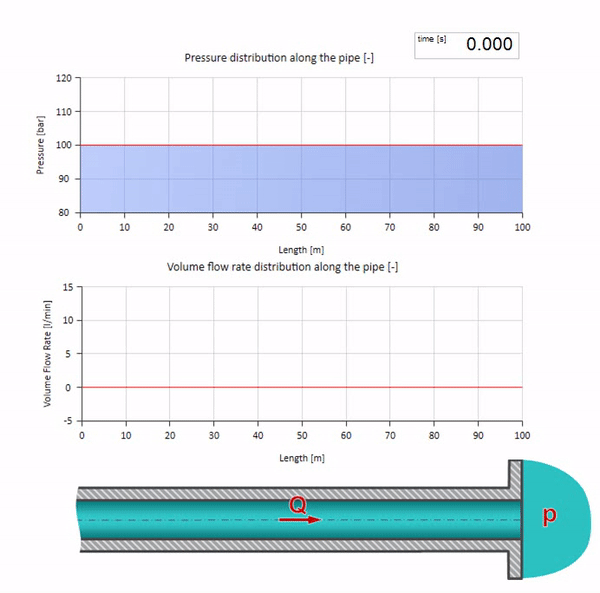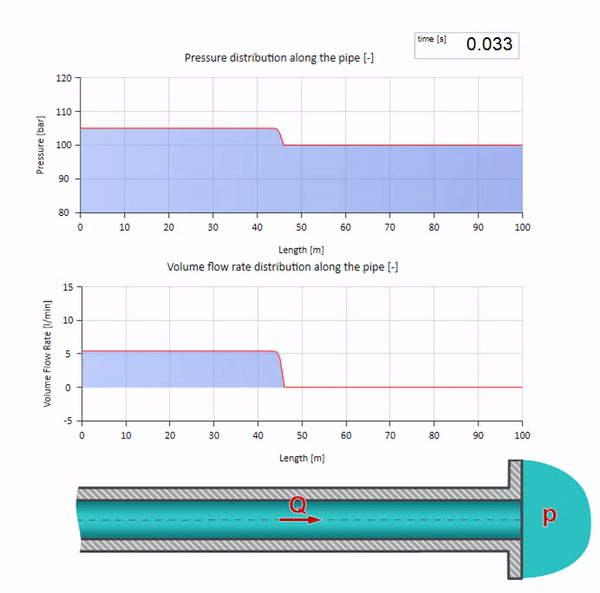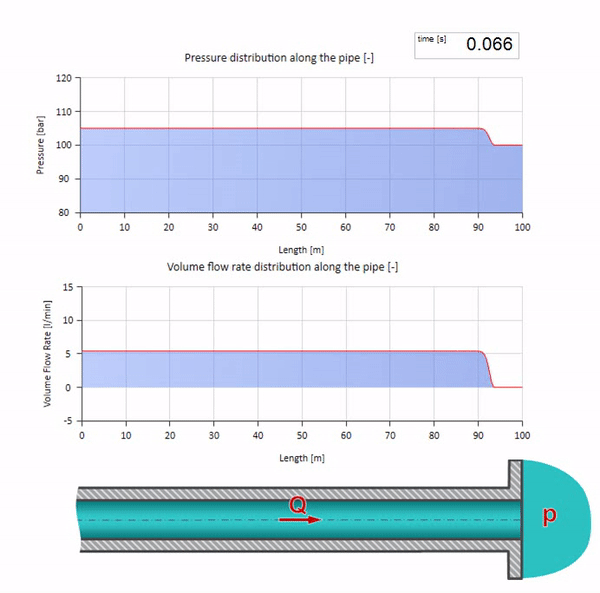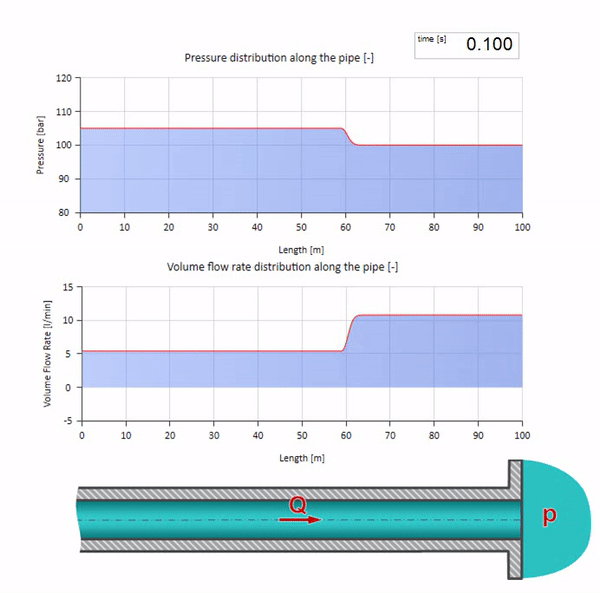
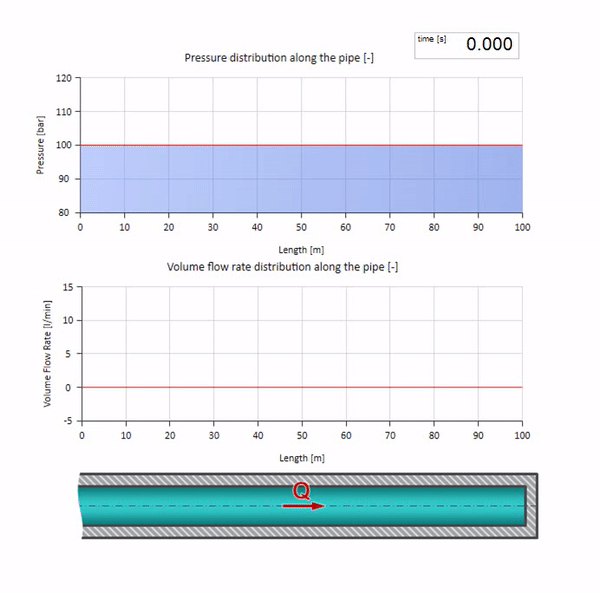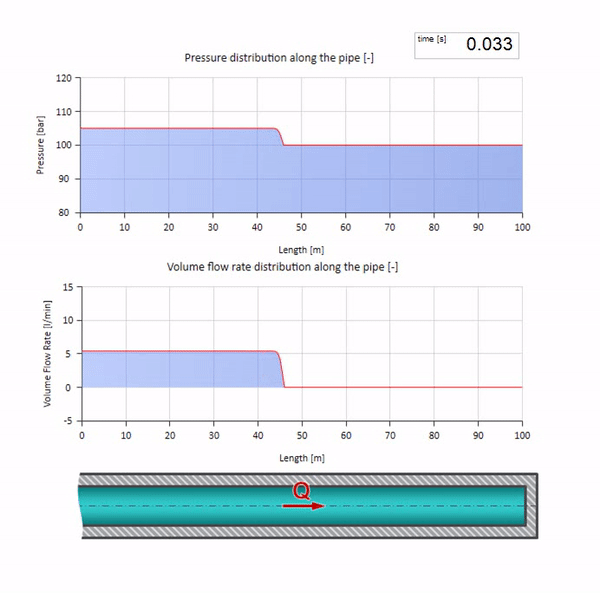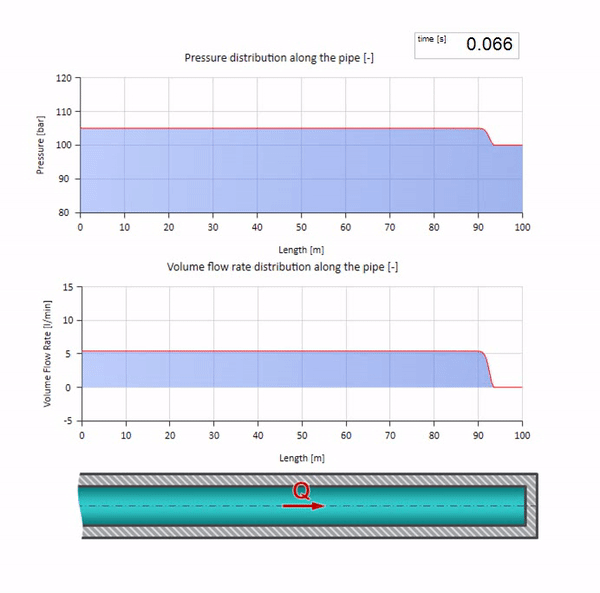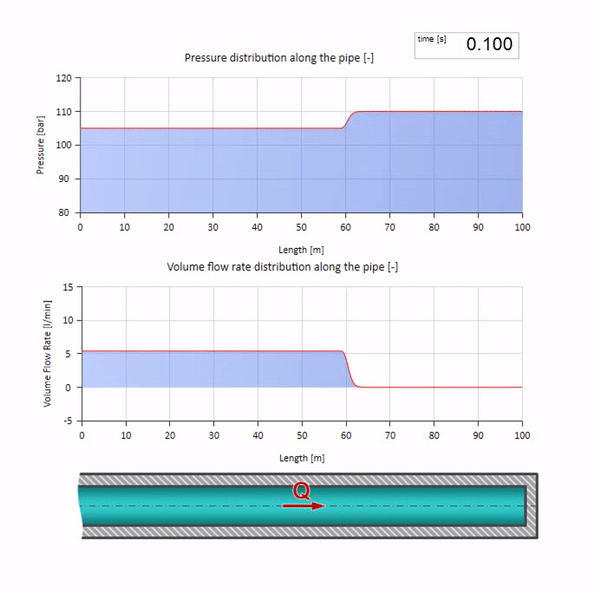
Wenn wir diese beiden Fälle kombinieren, erhalten wir einen klassischen Hydraulikdämpfer:

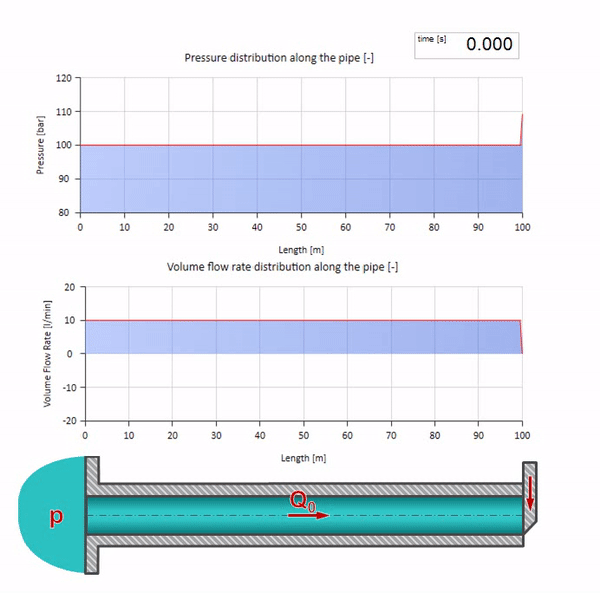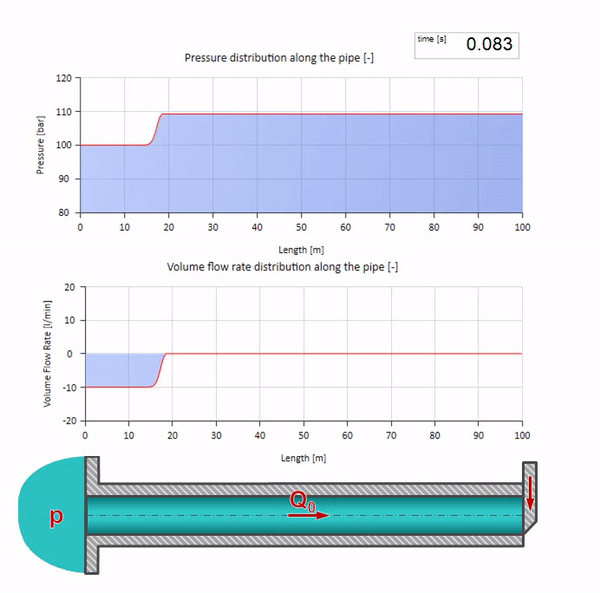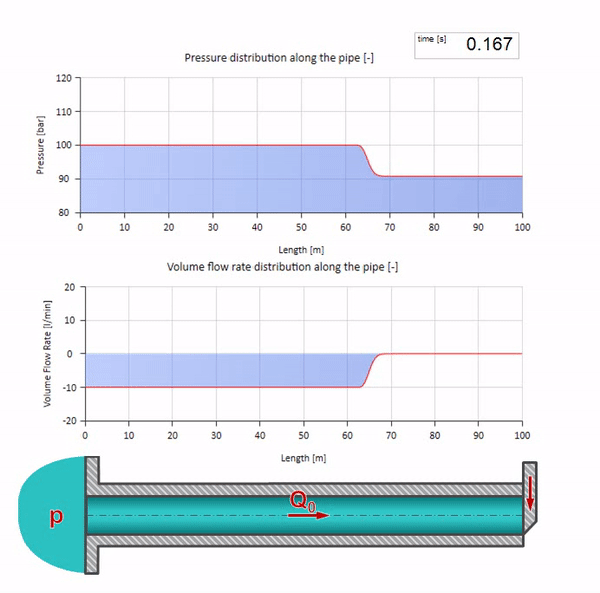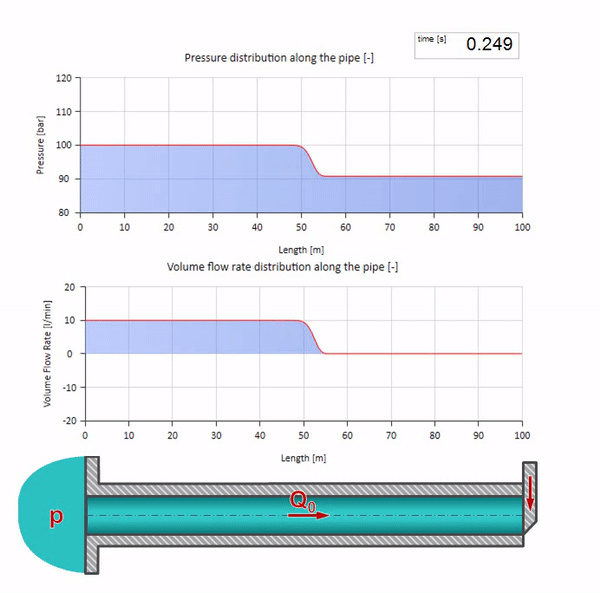
Hier gibt es zum anfänglichen Zeitpunkt einen Durchflusswert, der am rechten Ende des Rohrs sofort gleich Null ist (das Ventil schließt). Eine Welle fallender Strömung und steigenden Drucks beginnt sich nach links zu bewegen. Diese Wellen werden vom rechten Ende der Pipeline mit einer Impedanz von Null reflektiert. Ohne Reibung ist dieser Prozess endlos.
Interessanterweise können wir unter Verwendung der obigen Formeln die Zhukovsky-Gleichung für Wasserschläge ableiten:

$$

$$\ widehat p = Z_L \ widehat Q \;$$

Wir drücken die Durchflussrate durch die Geschwindigkeit aus, nehmen an, dass sie von einem bestimmten Wert auf Null fällt, und malen die Wellenimpedanz:

$$

$$\ widehat p = A \; v_0 \; \ frac {\ rho \; c} {\ A} = \ rho \; c \; v_0$$

Wir erhalten den Wert des Drucksprungs, der auftritt, wenn der Verschluss sofort geschlossen wird.

Anmerkungen

1. Ich wurde inspiriert, einen Artikel des Leiters eines Grundlehrbuchs über Hydraulik an der Fakultät für Wasserbau der Rhein-Westfälischen Technischen Universität Aachen zu schreiben, in dem meiner Meinung nach die Prozesse in Hydraulikleitungen am klarsten beschrieben werden (Grundlagen der Fluidtechnik Teil 1: Hydraulik, Hubertus Murrenhoff ISBN: 978-3-8440 -1223-1).
2. Animationen wurden im Programm SimulationX gemacht, die Berechnung wurde nach der Methode der Eigenschaften durchgeführt