So erstellen Sie zuverlässige Spielmechaniken in Excel. Teil 2

In diesem Teil werden wir das Problem der optimalen Platzierung von Waffen auf dem Panzer, der räumlichen Anordnung von Teleportern im MMORPG lösen und die Schlachten der vier Klassen von RPG-Charakteren ausgleichen.

Aufgaben zur Objektplatzierung

Tabellen für diesen Teil können hier heruntergeladen werden: ( SuperTank ) ( Teleporter, Teil 1 ) ( Teleporter, Teil 2 )

SuperTank: Das Problem ist gelöst!

Im ersten Artikel der Serie haben wir über ein Beispiel für eine Aufgabe für ein Spiel namens SuperTank gesprochen. Im zweiten Teil haben wir uns mit den Grundkonzepten der Entscheidungsmodellierung vertraut gemacht und ich habe über das Lösen eines einfachen Beispiels mit dem Tool "Suche nach Lösungen" in Excel gesprochen.

Jetzt können wir das im zweiten Teil gewonnene Wissen auf das SuperTank-Problem anwenden und beweisen, dass dieses Problem mit ihrer Hilfe einfach und schnell gelöst werden kann. Aktualisieren Sie Ihr Gedächtnis: SuperTank ist ein Spiel, in dem Sie auf einem benutzerdefinierten Panzer kämpfen können. Der Supertank sieht ungefähr so ​​aus:


Jeder Supertank kann eine beliebige Anzahl von Kanonen von fünf verschiedenen Typen haben:


Ein Supertank kann 50 Tonnen Waffen aufnehmen und ein Spieler kann 100 Credits ausgeben. Außerdem verfügt der Supertank über 3 „kritische Steckplätze“, in denen Spezialwaffen wie MegaRocket und UltraLaser platziert sind.

Die Tabelle für dieses Beispiel kann hier heruntergeladen werden .

Das Ziel ist es, Waffen aufzunehmen, die den durch den Supertank verursachten Schaden maximieren, ohne die Grenzen von 50 Tonnen, 100 Credits und 3 kritischen Slots zu überschreiten. Wir gehen auch davon aus, dass diese Tabelle alle erforderlichen Informationen enthält und dass Faktoren wie Reichweite, Häufigkeit und Genauigkeit nicht relevant sind oder bereits im Schadensparameter der entsprechenden Waffe berücksichtigt werden.

Um dieses Schema zu optimieren, geben wir diese Daten zunächst in die Tabelle ein. Direkt darunter werden wir eine weitere Tabelle hinzufügen, in der 5 „quantitative“ Zellen enthalten sind, um die Menge der 5 Waffentypen anzugeben.

Bis wir in diese Zellen den Wert 1 eingeben, nur um ihre Arbeit zu testen, aber dies sind unsere Entscheidungszellen. Wir werden das Solver-Tool bitten, die richtigen Werte für diese Zellen zu finden. Es ist möglich zu verstehen, dass dies Entscheidungszellen in Gelb sind, da wir weiterhin die im zweiten Teil beschriebenen Formatierungsregeln befolgen. Rechts von den „quantitativen“ Zellen fügen wir Berechnungszellen hinzu, die die Mengenwerte in den Entscheidungszellen mit den Werten für Schaden, Gewicht, Kosten und kritische Steckplätze aus der obigen Tabelle multiplizieren. Somit zeigt jede Zeile dieser Tabelle den Schaden, das Gewicht, den Preis und die kritischen Slots korrekt an, die für alle verwendeten Waffen in allen Kategorien von Waffen erforderlich sind.


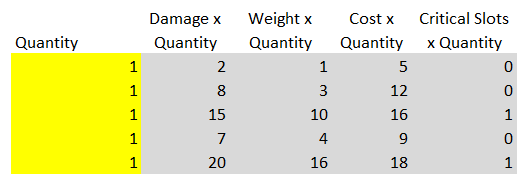
Im Folgenden wird außerdem ein Abschnitt erstellt, in dem alle Werte für Menge, Gewicht, Kosten und kritische Zeitnischen aus der obigen Tabelle zusammengefasst und mit den in den Aufgabenbedingungen (50, 100 bzw. 3) angegebenen Maximalwerten für Gewicht, Kosten und kritische Zeitnischen verglichen werden.


In Übereinstimmung mit den Formatierungsregeln aus dem zweiten Teil des Artikels sind die blauen Zellen oben die Kriterien aus den Bedingungen des Problems. Graue Zellen sind Berechnungszellen, die das Gesamtgewicht, die Kosten und die kritischen Slots basierend auf der Summe aus der Quantitätstabelle darstellen (d. H. Die Gesamtwerte der Spalten Gewicht x Menge, Kosten x Menge und kritische Slots x Menge). Schließlich stellt die orangefarbene Zelle den Gesamtschaden unseres Super-Panzers dar, basierend auf dem Gesamtschaden der Spalte Schaden x Menge aus der obigen Tabelle.

Bevor wir beginnen, lassen Sie uns unsere Tabelle benutzerfreundlicher gestalten. Wir werden die Gelegenheit von Excel nutzen, jeder Zelle einen Namen zuzuweisen und sieben Zellen in der letzten Berechnungstabelle eindeutige Namen zu geben. Dies ist optional, aber auf lange Sicht wird die Tabelle dadurch viel klarer (wenn die Zelle beispielsweise anstelle von $ F $ 21 den Namen MaxCriticalSlots trägt). Dazu wählen wir einfach eine Zelle aus, gehen zum Namenseingabefeld links neben dem Formelfeld und geben einen neuen Namen ein.


Lassen Sie uns nun endlich zu Excel Solver gehen und eine Lösung finden (gehen Sie zur rechten Seite der Registerkarte Daten und wählen Sie Solver aus. Wenn Sie es nicht sehen, gehen Sie zu Excel-Optionen Wählen Sie die Kategorie Add-Ins ("Add-Ons") aus, stellen Sie sicher, dass Excel-Add-Ins in der Dropdown-Liste "Verwalten" ausgewählt sind, klicken Sie auf Los ("Los ...") und stellen Sie sicher, dass Das Kontrollkästchen Solver-Add-In ist aktiviert.

Im Feld Ziel festlegen („Zielfunktion optimieren“) wählen wir die orangefarbene Zelle des Ziels aus und klicken dann auf das Optionsfeld Max („Maximum“). Wählen Sie im Feld Durch Ändern variabler Zellen die Entscheidungszellen aus (gelbe Zellen in der Spalte Menge der zweiten Tabelle). Klicken Sie unten auf die Schaltfläche Hinzufügen, um die folgenden Einschränkungen hinzuzufügen:

• Die Werte der Entscheidungszellen sollten im Bereich von 0 bis zu einem vernünftigen Maximum liegen (wir haben 50 gewählt, obwohl dies wahrscheinlich ein viel größerer Grenzwert als erforderlich ist). Es ist auch erforderlich, jede Lösungszelle auf eine Einschränkung "= Ganzzahl" zu setzen, da wir keinen Bruchteil der Bewaffnung haben können und Excel Solver jede Variable standardmäßig als reelle Zahl betrachtet, sofern nicht anders angegeben.

• Wir müssen auch die Werte der Gesamtkosten, des Gesamtgewichts und der Gesamtzahl der kritischen Steckplätze auf die Werte aus den Bedingungen des Problems beschränken. Das Bild des Dialogfelds zeigt, dass sie jetzt praktische Namen haben, die wir der unteren Tabelle hinzugefügt haben, wodurch das Dialogfeld leichter zu lesen ist.

Jetzt klicken wir auf die Schaltfläche Lösen („Eine Lösung finden“) und nach einer kurzen Wartezeit gibt Solver die Mengenwerte ein, die uns Folgendes geben:

• 1 Maschinengewehr
• 3 Raketen
• 2 MegaRockets
• 1 Laser
• 1 UltraLaser

All dies verursacht einen Gesamtschaden von 83 Einheiten und benötigt genau 50 Tonnen, 100 Credits und 3 kritische Slots. Sie können sehen, dass sich die beste Lösung mit der Solver-Laufzeit nicht ändert. Wenn Sie diese Werte zurücksetzen und eine zweite Optimierung durchführen oder zu Optionen gehen und den Startwert ändern, erhalten wir immer noch dieselben Werte. Wir können nicht zu 100% sicher sein, dass diese Lösung optimal ist. Angesichts der Tatsache, dass Solver es nach mehreren Optimierungsdurchläufen nicht geschafft hat, sie zu verbessern, ist es sehr wahrscheinlich, dass es sich um ein echtes Optimum handelt und nicht nur um ein lokales Maximum.

Das Problem ist gelöst!

Zusätzliche Verwendungen

Das Coole ist, dass wir das Problem nicht nur viel schneller gelöst haben, als wir es manuell lösen konnten, sondern es auch so eingerichtet haben, dass wir testen können, welche Waffen im SuperTank-Spiel mit verschiedenen Parametern (Gewicht, Kosten, kritische Slots) am nützlichsten sind. Dies bedeutet, dass wir die Auswirkung verschiedener Änderungen dieser Parameter auf das SuperTank-Spiel relativ einfach ändern können. Wenn wir ein neues alternatives Super-Tank-Modell hinzufügen möchten, das leichter, schwerer oder mit einer anderen Anzahl kritischer Slots ausgestattet ist, kann dies sehr einfach erfolgen.

Durch Ändern all dieser Parameter können wir auch die relative Nützlichkeit jeder dieser Waffen verstehen und schnell feststellen, welche zu nützlich, nicht nützlich genug ist, einen Preis hat, der für ihr Gewicht und ihren Schaden nicht geeignet ist, und so weiter.

Auch hier geht es darum, dass wir mit einem solchen Tool den Entwurfsraum viel schneller durchsuchen können, als wir es manuell könnten. Es bietet uns eine bequeme Möglichkeit, die Auswirkungen solcher Änderungen für jede inkrementelle Konstruktionslösung zu bewerten, die wir entwickeln können, sei es das Ändern der Parameter der Waffe oder des Supertanks selbst, das Hinzufügen neuer Waffen oder Modelle von Supertanks sowie das Hinzufügen neuer Parameter (sagen wir, die Größenbeschränkung liegt in Kubikmetern).

Um zu verstehen, was ich meine, gehen Sie zur blauen Zelle "Max Cost" und ändern Sie den Wert von 100 auf 99. Führen Sie nun Solver erneut aus, und Sie erhalten ein völlig anderes Waffenlayout:

• 0 Maschinengewehre
• 2 Raketen
• 3 MegaRockets
• 3 Laser
• 0 UltraLaser

Ein solches Schema ergibt einen etwas niedrigeren Schadensindex (82 statt 83), unterscheidet sich jedoch grundlegend von dem vorherigen.

Wenn Sie den Wert für die maximalen Kosten auf 101 oder 102 festlegen und die Berechnung erneut durchführen, besteht die Möglichkeit, dass wir eine Konfiguration erhalten, die der ersten ähnlich ist oder mit dieser übereinstimmt. wie auch immer, der Schaden bleibt gleich 83 (Schemata können sich ändern, da es in solchen Fällen mehrere optimale Schemata gibt). Wenn Sie jedoch die maximalen Kosten auf 103 festlegen, sollten Sie Folgendes erhalten:

• 1 Maschinengewehr
• 4 Raketen
• 2 MegaRockets
• 0 Laser
• 1 UltraLaser

Das erhöht den Gesamtschaden auf 84.

Das ist interessant: Diese Anordnung der Waffen unterscheidet sich sehr von den ersten beiden.


Wie Sie sehen, erhalten wir ein unerwartetes Ergebnis: Die optimale Auswahl der Waffen in unserem Schema hängt stark von den Parametern des Supertanks ab und kann selbst bei kleinen Änderungen dieser Parameter erheblich variieren. Darüber hinaus erhalten wir alle möglichen nützlichen Informationen: Alle fünf Waffentypen sind in mindestens zwei der drei Super-Panzer-Einstellungen nützlich, und Raketen und MegaRockets sind offensichtlich in allen drei nützlich. Dies scheint uns zu sagen, dass alle fünf Waffentypen gut ausbalanciert sind, dh im Verhältnis zueinander nützlich sind und gleichzeitig einzigartig bleiben.

Und wie Sie auch feststellen können, bietet uns eine solche Modellierung und Optimierung von Lösungen eine hervorragende Möglichkeit, schnell Suchvorgänge in einer lokalen Nachbarschaft durchzuführen und erneut zu optimieren. Bei einigen Arten von Aufgaben können wir dominante Strategien und Exploits von Spielern erkennen, die auf andere Weise schwer oder unmöglich zu finden sind.

Teleports - Wurmlöcher

Wenn Sie sich die letzten beiden Beispiele ansehen (das Beispiel der Steuersätze in einem strategischen Spiel und SuperTank), könnten Sie denken, dass solche Techniken nur in Fällen anwendbar sind, in denen Benutzer mit Zahlen arbeiten. Aber du wirst absolut falsch liegen! Wie wir sehen werden, gibt es viele Beispiele dafür, wie Sie die Vorteile der Optimierung von Designelementen nutzen können, die für Benutzer nicht nur nicht wie Zahlen aussehen, sondern überhaupt nicht so aussehen!

Sie können auch denken, dass die Entscheidungsmodellierung nur auf Entscheidungen anwendbar ist, die Spieler in Spielen treffen können. Dies gilt auch nicht: In einigen Fällen können sie zur Modellierung verwendet werden, um Ihre eigenen Lösungen als Designer zu optimieren.

Angenommen, Sie arbeiten an einem Space-MMORPG. Eines Tages kommt Ihr Hauptdesigner mit sichtbarer Angst auf seinem Gesicht auf Sie zu. "Wir führen eine Neugestaltung des Omega-Sektors durch", sagt er. „Und wir hatten ein Problem. Wir planen, ein paar Wurmloch-Teleporter "in diesem Segment der Welt" hinzuzufügen, aber wir können uns nicht darauf einigen, wo sie platziert werden sollen.

"Wie viele Teleporter?", Fragen Sie.

„Wir wissen es noch nicht. Wahrscheinlich drei, aber es können zwei bis vier sein. Wir sind uns noch nicht sicher. “ Dann zeigt er Ihnen eine Karte, die so aussieht:


"Was ist das?" Sie fragen.

„Dies ist eine Karte des Omega-Sektors. Oder zumindest die Sternensysteme, die ein Spieler in diesem Quadranten besuchen kann. Wir müssen bestimmen, in welchen Zellen sich die Wurmlöcher befinden sollen. “

„Na dann, und nach welchen Regeln werden sie aufgestellt? Ist es möglich, das Wurmloch mit dem Sternensystem in einem Quadranten zu platzieren? “

„Wir möchten, dass Sie die Wurmlöcher so platzieren, dass der Abstand zwischen Sternensystemen und dem nächsten Wurmloch so gering wie möglich gehalten wird. Und ja, Sie können sie in denselben Quadranten wie das Sternensystem setzen. Es sind nur kleine Teleporter, die im Weltraum hängen, sodass sie überall platziert werden können. Und denken Sie daran, dass wir noch nicht entschieden haben, wie viele es sein sollen. Geben Sie mir also Lösungen für 2, 3 und 4 Wurmlöcher. “

Wie formuliere ich dieses Problem und wie löse ich es?

Teleporter optimieren!

Beginnen wir mit der Vorbereitung der Lösungszellen. Wir bezeichnen die vier Teleports als A, B, C und D. Wir wissen, dass jeder Teleport im Wesentlichen nichts anderes als die Koordinaten (x, y) auf der Sternenkarte des Omega-Sektors ist. Wir wissen auch, dass wir die Anzahl der aktiven Teleports angeben müssen, daher fügen wir eine Zelle hinzu, in der Sie die Anzahl der Teleports festlegen können. Wir verwenden Teleport D nur, wenn 4 Wurmlöcher verwendet werden, und C nur, wenn wir 3 oder mehr haben.


Nachfolgend erstellen wir eine Tabelle zur Berechnung der Entfernung von jedem Sternensystem zum nächsten Teleport. Diese Tabelle sieht folgendermaßen aus:


Links blau zeigt die Koordinaten jedes Sternensystems auf der Karte. Jede Reihe ist ein Sternensystem. Wir haben sie einfach von der Karte des Omega-Sektors übertragen, die uns der führende Designer gegeben hat.

Rechts berechnen wir die Entfernung zu jedem der vier Teleporter. Dies ist nur ein Satz von Pythagoras. Die Entfernung wird als Quadratwurzel der horizontalen und vertikalen Entfernungen zwischen dem Sternensystem und dem Teleport berechnet:

= SQRT (($ B14-Ax) ^ 2 + ($ C14-Ay) ^ 2)

(Keine Sorge - ich verspreche, dass dies die schwierigste Mathematik ist, die wir in der Reihe treffen werden!)

Wir nehmen die X- und Y-Koordinaten jedes Sternensystems aus den blauen Zellen der obigen Tabelle und die X- und Y-Koordinaten jedes Teleports (Zellen mit den Namen Ax und Ay für Teleport A in der oben gezeigten SQRT () -Funktion) aus den gelben Lösungszellen oben.

Schließlich nehmen wir das Minimum dieser vier Werte in der Spalte Dist to Closest, dh wir verwenden einfach die Funktion MIN (), um das Minimum von vier Werten auf der linken Seite zu bestimmen. Dann fassen wir die gesamte Spalte unten zusammen; Die Summe ist die Zielzelle.

Möglicherweise haben Sie bemerkt, dass im obigen Screenshot alle Zellen auf Dist to D gesetzt sind. Der Grund dafür ist, dass wir die Zelle "Anzahl der Teleporter?" Verwenden im oberen Bereich des Lösungsmodells, in dem Sie die Anzahl der berücksichtigten Teleports konfigurieren können. Wenn die Anzahl der Teleporter 2 ist, verwenden wir den Wert 99 sowohl in Dist zu C als auch in Dist zu D, und wenn er 3 ist, wird der Wert 99 nur in der Spalte Dist zu D verwendet. Daher ignoriert jedes Sternensystem alle unnötigen Teleporter bei der Berechnung der Entfernung zum nächsten Teleport bei 2 oder 3 Teleports.

Jetzt starten wir Solver:


Die Zielzelle ist die Summe am unteren Rand der Spalte Dist to Closest. Beachten Sie, dass wir hier im Gegensatz zu anderen Beispielen das Optionsfeld „An: Min“ verwenden möchten, da wir einen Mindestabstand zwischen allen Sternensystemen und Teleportern benötigen, keinen Maximalabstand.

Im Folgenden werden acht gelbe Zellen zum Lösen der X- und Y-Koordinaten der Wurmlöcher A, B, C und D als Zellen der Lösungen angegeben (durch Ändern variabler Zellen). Im Abschnitt Einschränkungen wird jede der Koordinaten als ganzzahliger Wert im Bereich von 0 bis begrenzt 12. Beachten Sie, dass wir für diese Lösungszellen eine Ganzzahlbeschränkung verwenden, da der Hauptdesigner nur wissen möchte, in welcher Zelle sich jeder Teleport befindet. Wir können diese Einschränkung jedoch leicht überspringen, wenn der Designer Materialkoordinaten benötigt.

Wenn wir nach der Anzahl der Teleporter fragen? Werte 2, 3 und 4, und nacheinander starten wir Solver bei jedem Wert. Wir erhalten die folgenden Konfigurationen:


Mit diesen Informationen können wir uns an den führenden Designer wenden und ihm die optimalen Standorte für den Standort einer beliebigen Anzahl von Teleportern im Bereich von 2 bis 4 anzeigen. So sehen die optimalen Standorte der „Wurmlöcher“ für 2, 3 und 4 Teleporter auf der Karte aus (grün dargestellt).


Die Tabelle für dieses Beispiel kann hier heruntergeladen werden .

Habe ich über den Ninja gesprochen?

"Erstaunlich", sagt der Hauptdesigner, aber man sieht Leiden in seinem Gesicht. „Äh, aber ich habe vergessen dir zu sagen, dass einige dieser Systeme von Weltraum-Ninja bewohnt werden. Und wir möchten, dass die Systeme mit dem Ninja weiter von den „Wurmlöchern“ entfernt sind, damit sich die Spieler nicht übermäßig bedroht fühlen. "

„Wow. Dies ändert den Fall völlig. “

„Richtig. Darüber hinaus gibt es in einigen Sternensystemen nicht nur eine, sondern zwei Kolonien, dh sie sind doppelt so wichtig wie die Nähe zu Teleportern. Oder es ist doppelt so wichtig, weiter zu sein, wenn es sich um ein System mit zwei Kolonien von Weltraum-Ninja handelt. So sieht die Karte jetzt aus: "


Er fährt fort: „Jede negative Zahl ist eine Kolonie von Weltraum-Ninjas. Das System mit der Nummer 2 enthält zwei menschliche Kolonien und mit der Nummer -2 enthält es zwei Kolonien des Ninja. Können Sie mir sagen, wo ich in diesem Fall Teleporter platzieren soll? “

"Sag mir, zumindest hast du bereits entschieden, wie viele Teleports es geben wird: 2, 3 oder 4?", Fragst du sarkastisch.

"Ich fürchte noch nicht."

Wir lösen unter Berücksichtigung des Ninja

Um dieses Problem zu lösen, müssen wir der Tabelle eine neue Spalte hinzufügen, die das Gewicht der Tabelle angibt. Wir werden es den "Multiplikator" nennen. Wir multiplizieren diesen Wert einfach mit dem Wert in der Spalte Dist to Closest.

Wenn wir dies tun, ändert Dist to Closest seine Bedeutung geringfügig. Dies ist nicht die Entfernung zum nächsten Sternensystem, da sich der Wert für Ninja-Sternensysteme um das -1-fache ändert. Es ähnelt allgemeineren „Punkten“ (Punktzahl), also nennen wir sie so.


Somit geben Punkte jetzt den kumulativen Wert an. Indem wir es minimieren, bemühen wir uns, Solver so nahe wie möglich an Systemen mit menschlichen Kolonien und gleichzeitig so weit wie möglich von besiedelten Ninja-Systemen entfernt zu sein.

Jetzt erhalten wir folgende Ergebnisse:


Wie Sie sehen können, haben wir hier die Konfiguration von Teleportern, die sich jeweils stark von einfacheren Versionen ohne Ninja unterscheiden.


Die Tabelle für diese erweiterte Version des Teleport-Beispiels kann hier heruntergeladen werden .

Wie Sie sehen, konnte unser Lösungsmodell diese nicht triviale Aufgabe sehr schnell lösen und wir können sie an sich ändernde Anforderungen anpassen.

Diese Aufgabe gehört zu der Klasse von Aufgaben, die als „Objektzuweisungsaufgaben“ bezeichnet werden und im Bereich der Betriebsführung sehr gut untersucht sind. Wie Sie jedoch sehen können, können sie möglicherweise sowohl im Spieldesign als auch im Leveldesign verwendet werden, und die Lösung ist in Excel einfach (wenn nicht trivial).

Player-vs-Player

:

In den vorherigen drei Teilen dieser Artikelserie haben wir uns mit dem Konzept der Modellierung und Optimierung von Lösungen sowie mit dem Tool „Solver“ des Excel-Pakets vertraut gemacht. Wir haben gezeigt, wie sie verwendet werden können, um die optimalen Steuersätze einer Stadt in der 4X-Strategie zu berechnen, die optimale Platzierung von Teleportern in einem Weltraumspiel zu bestimmen und die optimale Anordnung der Waffen für die im ersten Teil beschriebene Superpanzeraufgabe auszuwählen.

Eine natürliche Frage stellt sich: Was ist mit dem Balancieren des Spiels? Ist es möglich, ähnliche Techniken auf alle Arten komplexer Balancing-Aufgaben anzuwenden, die in vielen verschiedenen Arten von Spielen zu finden sind, insbesondere in Strategien, RPGs und MMORPGs?

Die Antwort auf diese Frage lautet natürlich ja, aber mit vielen Vorbehalten. Insbesondere Tabellenkalkulationen weisen viele Einschränkungen auf, da sie in den meisten nicht trivialen Fällen das Spiel nicht genau beschreiben. Daher wird es für uns schwierig sein, mithilfe von Optimierungstechniken einen zuverlässigen Ausgleich durchzuführen. Die eigentlichen Ausgleichsaufgaben der meisten Spiele werden weit über das hinausgehen, was wir in einer Tabelle modellieren können. Die Simulation des Spiels selbst ist normalerweise zu kompliziert, hat viele "bewegliche Teile" und wird oft in Echtzeit ausgeführt. Wenn wir versuchen, eine diskrete Simulation durchzuführen, können alle Arten von Problemen auftreten.

Daher, wenn wir ähnliche Techniken zum Ausgleichen von Klassen in MMORPGs wie WildStar oder in strategischen Spielen wie verwenden wolltenPlanetarische Vernichtung , um zumindest eine gewisse Genauigkeit und Nützlichkeit sicherzustellen, müssten wir sie in die Simulation des Spiels selbst integrieren.

Darüber hinaus können einige Aspekte des Ausgleichs nicht automatisiert werden. Wie wir im ersten Teil des Artikels erklärt haben, ist es unmöglich, das Spielerlebnis automatisch anzupassen.

Das Beste, auf das wir hoffen können, ist daher die Demonstration eines einfachen Beispiels, das einen allgemeinen Ansatz für Aufgaben dieser Art veranschaulicht: Anhand eines einfachen Beispiels in Excel lernen wir, wie man die Formulierung dieser Art von Ausgleichsproblemen angeht und sie optimiert. Wir werden zeigen, dass Solver zumindest für ein Beispiel eines einfachen Kampfes mehrere RPG-Klassen relativ zueinander ausgleichen kann. Dann können Sie diese Grundstruktur als Grundlage für die Lösung solcher Optimierungsprobleme mit einem komplexeren Schema verwenden, das tiefer in die Simulation des Spiels integriert ist.

Wir hoffen, dass Sie bei uns alle Tricks lernen und sehen, was dieses einfache Beispiel uns geben kann.

Unausgeglichen

Es gibt keine einheitliche Definition des Wortes „Balancing“. Es hat viele Bedeutungen und hängt normalerweise vom Kontext des betreffenden Spiels ab. Unter verschiedenen Bedingungen kann das Balancieren mit dem Einrichten mehrerer Klassen von Charakteren zusammenhängen, um deren Fähigkeiten in einem Rollenspiel gleichzusetzen, mit der Anzahl der Kräfte von Gegnern, die in einem strategischen Spiel gegeneinander kämpfen, oder mit dem Anpassen der Kosten verschiedener Einheiten oder Ressourcen entsprechend ihrer Nützlichkeit.

Die beste Definition von "Balancing" hängt normalerweise von den Designzielen des betreffenden Spiels ab. Da diese Ziele jedoch beliebig sein können, ist es unmöglich, a priori zu bestimmen, was Balancing für Spiele im Allgemeinen wirklich bedeutet.

Einige Spieler neigen dazu zu glauben, dass das Balancieren im Kampf gleichen Schaden bedeutet. Dies gilt insbesondere für MMORPGs, bei denen sich Spieler häufig darüber beschweren, dass der Schaden pro Sekunde (DPS) einer Klasse im Vergleich zu den anderen zu gering oder zu groß ist.

Natürlich können Klassen nicht nur durch DPS ausgeglichen werden. Es ist akzeptabel, dass eine Klasse einen größeren DPS als eine andere hat, dies sollte jedoch durch andere Faktoren ausgeglichen werden, die den Gesamtnutzen der Klasse einschränken, z. B. ein verringertes Überleben oder einen weniger langfristigen DPS im Vergleich zu einem kurzfristigen DPS.

Winziges MMO

Stellen Sie sich vor, wir erstellen ein neues Projekt, ein sehr vereinfachtes Massively Multiplayer Online-Rollenspiel namens „Tiny MMO“. Im Rahmen der Designentwicklung bemühen wir uns, die vier Klassen für Spieler-zu-Spieler-Kämpfe (PVP) so auszugleichen, dass alle vier Klassen im Kampf gegeneinander relativ gleich sind und es keine eindeutige „bessere“ oder „schlechtere“ Klasse gibt Sie können gegen andere Klassen kämpfen.

Obwohl Tiny MMO ein Echtzeitspiel ist, dauert die Aktion jedes Spielers genau 3 Sekunden, sodass wir sie diskretisieren können, indem wir sie als rundenbasiertes Spiel präsentieren, bei dem jede Runde einen Anteil von drei Sekunden am Spiel darstellt.

Spieler in diesem Spiel können eine von vier Charakterklassen auswählen:

• Krieger fügt den größten Schaden zu.
• Magier wirken Zauber aus der Ferne und haben die größte Angriffsreichweite aller vier Klassen
• Heiler (Heiler) wird automatisch behandelt und stellt für jede Runde einen bestimmten Teil seiner Gesundheit wieder her
• Barbar (Barbar) hat die meiste Gesundheit

Dies ist alles, was wir über diese vier Klassen wissen, und wir müssen die Anfangsparameter Gesundheit (HP), Schaden, Heilung und Reichweite der Angriffe für alle vier Klassen festlegen. Wir müssen sie so ausbalancieren, dass jede Klasse einzigartig ist und sich ihre Eigenschaften erheblich von allen anderen Klassen unterscheiden. Damit sich jedoch herausstellt, dass jede Klasse in Bezug auf die anderen drei Klassen so „ausgeglichen“ wie möglich ist.

Mit anderen Worten, wir bemühen uns, die folgende Tabelle zu optimieren:


Während wir temporäre Werte verwenden und davon ausgehen, dass jede Klasse mit 50 HP beginnt, 10 Schaden pro Runde verursacht, 0 HP pro Runde heilt und eine Angriffsreichweite von 40 Metern hat. Jeder Charakter bewegt sich mit einer Geschwindigkeit von 10 Metern pro Runde. Da das Design angibt, dass sich alle vier Klassen von Zeichen mit derselben Geschwindigkeit bewegen können, betrachten wir diesen Wert als konstant und geben die Bewegungsgeschwindigkeit nicht in die Tabelle der Entscheidungsvariablen ein.

Dies ist offensichtlich eine Fallstudie mit einem sehr vereinfachten Schadensmodell. Dies ist ein kontinuierlicher Durchschnittswert des Schadens pro Sekunde, der den Unterschied zwischen Pulsschaden und Langzeitschaden sowie Mana und andere Mechaniken, die die Angriffsfähigkeiten von Klassen verändern, ignoriert. Wir werden nur eine Art von Schaden haben, was ziemlich unrealistisch ist, da die meisten Klassen Dutzende Arten von Schaden haben und wir ein KI-System implementieren müssen, das den Angriff in jeder Runde auswählt. Darüber hinaus hat Schaden in den meisten Spielen ein zufälliges Element, aber im Moment werden wir dies weglassen und davon ausgehen, dass die Variabilität des Schadens nicht so groß ist, dass das Ergebnis des Kampfes zwischen den beiden Klassen erheblich beeinflusst wird.

Natürlich ist es unwahrscheinlich, dass ein in Excel durchgeführter Ausgleich ideal ist oder mit dem endgültigen Ausgleich des Spiels übereinstimmt. Sie wird viele Iterationen von Spieltests durchlaufen müssen. Wenn wir jedoch ein oder zwei Stunden brauchen, um eine gute erste Option für unser Spiel in Excel zu erhalten, nähern wir uns zumindest viel eher den qualitativen Parametern des anfänglichen Gleichgewichts, wodurch wir uns dem endgültigen Gleichgewicht nähern, das wir erreichen möchten.

Siegertabelle

Wir müssen vier Klassen in einem Einzelkampf gegeneinander ausbalancieren. Da wir nur 4 Klassen haben (Krieger, Magier, Heiler und Barbar), gibt es 6 mögliche Kombinationen verschiedener Klassen:

• Krieger - Magier
• Krieger - Heiler
• Krieger - Barbar
• Magier - Heiler
• Magier - Barbar
• Heiler - Barbar

Dieses Auswuchten kann ziemlich kompliziert sein. Selbst in unserem eher einfachen Fall mit vier Klassen haben wir sechs Beziehungen zwischen Klassen, genauso wie wir sechs Linien zwischen vier Punkten eines Quadrats zeichnen können.


Jedes Mal, wenn wir einen der Parameter einer der Klassen geringfügig ändern möchten, wirkt sich diese Änderung auch auf das PvP-Gleichgewicht zwischen diesem Klassenpaar und den beiden anderen Klassen aus. Diese Verbindung zwischen Potenz und Gesetz wird nur mit zunehmender Anzahl von Klassen zunehmen, und Entscheidungen über den Ausgleich des PvP zwischen zwei Klassenpaaren, die „im luftleeren Raum“ getroffen werden, ohne alle anderen Wechselwirkungen zu berücksichtigen, können sehr gefährlich werden.

Idealerweise würden wir eine Art zu schaffen , wie Tabelle von Siegenwie der unten gezeigte. Wenn wir einen Kampf zwischen jedem dieser 6 Paare in einer Tabelle simulieren können, können wir für jedes der 6 Paare eine bestimmte "Punkt" -Variable generieren. Je mehr Punkte, desto besser, sodass wir alle sechs Punkte kombinieren können, um eine Zielfunktion zu generieren.


Beachten Sie, dass in der obigen Tabelle die Zellen entlang der Diagonalen Null sind, da sie Paare derselben Klasse bezeichnen, die per Definition ausgeglichen werden. Außerdem sind die Zellen in der oberen rechten Ecke ebenfalls Null, da sie genau die gleichen Paare wie in den Zellen in der unteren linken Ecke bezeichnen.

Bereiten wir nun das Modell für den Kampf zwischen zwei verschiedenen Klassen vor.

"Kampfsimulator"

Wir werden jedes Klassenpaar in einem Abstand von 100 Metern voneinander arrangieren. Jeder Charakter hat 3 Sekunden Zeit zum Angriff, daher können wir uns dies als rundenbasierte Simulation vorstellen, bei der jede „Bewegung“ 3 Sekunden bedeutet. Bei jedem „Zug“ greift jeder Charakter entweder den anderen an, wenn er sich in Reichweite des Angriffs befindet, oder bewegt sich weiter, um die Distanz zu verringern.

Die Simulation sieht folgendermaßen aus:


Oben sind zwei Charaktere zu sehen, die in die Schlacht eingetreten sind: in diesem Fall Magier (Klasse 1) und Heiler (Klasse 2). Die linke Spalte zeigt den aktuellen Abstand zwischen den beiden simulierten Zeichen.

Für jedes Zeichen lauten die Spalten:

• Max Range : , . .
• Healing : , .
• HP : . HP , . , .
• Damage : , , . , 0.
• Angriffe? : Diese Spalte prüft, ob sich der Charakter innerhalb des Angriffsbereichs befindet. Wenn ja, bedeutet dies, dass der Charakter in der aktuellen Runde angreift. Wenn nicht, rückt der Charakter näher, um einen anderen Charakter zu erreichen.

Somit bewegen sich beide Charaktere aufeinander zu und greifen dann an, bis einer von ihnen oder beide sterben. Jeder Charakter bewegt sich alle 3 Sekunden 5 Meter (5 Meter pro "Zug"). Wenn sich beide Charaktere aufeinander zu bewegen, ändert sich die Reichweite in jeder Runde um 10 Einheiten und um 5 Einheiten, wenn sich nur einer von ihnen bewegt. Das Spiel selbst ist so strukturiert, dass beide Charaktere gleichzeitig beginnen können, sich zu bewegen. Danach ist der Zug gleichzeitig zulässig, sodass beide Charaktere gleichzeitig sterben können.

Als nächstes müssen wir die Wertung für diese Tabelle einrichten und einen numerischen Wert generieren, der angibt, wie „gut“ der Kampf war. Mit anderen Worten, wie nah sind wir an der Erreichung unserer Designziele.

Offensichtlich wollen wir, dass beide Charaktere am Ende des Kampfes tot sind oder zumindest dem Tod so nahe wie möglich sind. Wenn der Kampf ausgeglichen ist, sollten beide Kampfklassen die Gesundheit des Feindes am Ende des Kampfes minimieren.

Dies allein reicht jedoch nicht aus. Wenn wir die Wertung auf diese Weise organisieren, maximiert der Optimierer einfach die Schadenswerte, sodass sich beide Charaktere sofort gegenseitig töten! (Wenn Sie neugierig sind, ändern Sie die dem Artikel beigefügte Tabelle, um sich selbst davon zu überzeugen.) Natürlich streben wir nicht den sofortigen Tod an: Wir brauchen beide Charaktere, um am Ende des Kampfes tot oder fast tot zu sein, aber gleichzeitig wollen wir, dass der Kampf eine angemessene Zeit dauert.

Mit anderen Worten, wir bemühen uns nicht nur um ein relativ gleiches Gleichgewicht aller Klassen gegeneinander; Wir wollen auch das Gleichgewicht interessant machen , einschließlich der Kämpfe, die eine angemessene Zeit dauern.

Um eine solche Bilanzschätzung zu erstellen, müssen rechts neben jeder Tabelle mehrere Zellen erstellt werden. Dauer gibt die Dauer des Kampfes an; Sie zählt die Anzahl der Zeilen in der Tabelle, in denen beide Zeichen noch leben. Total HP berechnet die gesamten Trefferpunkte der beiden überlebenden Charaktere. Idealerweise sollte es 0 sein, dh bis zum Ende des Kampfes sterben beide Charaktere.


Und schließlich kombiniert Score die Dauer und die Gesamtanzahl der Trefferpunkte in der Form (Dauer / (1 + Gesamt-HP)). Beachten Sie, dass wir dem Divisor 1 hinzugefügt haben, da Total HP 0 sein könnte. In diesem Fall würden wir einen Fehler durch Division durch Null erhalten. Auf diese Weise können wir garantieren, dass wir den Optimierer dafür belohnen, dass er die maximale Dauer des Kampfes und den minimalen Wert der Summe der Trefferpunkte ermittelt.

(Beachten Sie, dass wir in jeder „Simulation“ eines Kampfes von Klasse zu Klasse 17 Linien haben. Dies bedeutet, dass wir im Wesentlichen eine Entwurfsentscheidung getroffen haben, dass der Kampf ungefähr 17 Runden dauern soll. Wenn wir möchten, dass der Kampf kürzer ist oder länger können Sie die Anzahl der Zeilen ändern, die Formel zur Berechnung der Punktzahl bearbeiten und eine zweite Optimierung entsprechend durchführen.)

Schließlich nehmen wir diese sechs Score-Werte (einen für jede Tabelle) und verwenden sie in der obigen Victory-Tabelle, um die Ergebnisse des Kampfes zwischen jedem Klassenpaar anzuzeigen.

Sie können diese sechs Bewertungswerte einfach zusammenfassen und das Ergebnis als endgültigen Bewertungswert verwenden. Wenn wir dies jedoch tun, wird Solver höchstwahrscheinlich kein gutes Gleichgewicht zwischen der höchsten und der niedrigsten Bewertung für einzelne Kämpfe finden können und wird auch für einige Klassenpaare sehr hohe Bewertungen für andere und niedrige Bewertungen erhalten. Dies ist nicht das, was wir wollen: Wir brauchen alle Noten, um hoch zu sein, und wir bemühen uns, sie alle zu erhöhen. Um dies zu beheben, multiplizieren wir die Summe der Noten mit der kleinsten Note in der Gruppe (mithilfe der Excel MIN () -Funktion), damit Solver sich auf die Noten mit dem niedrigsten Wert konzentriert.

Einschränkungen hinzufügen

Wir sind noch nicht fertig. Wenn Sie ein Lösungsmodell mit aktuellen Parametern optimieren, werden die Klassen höchstwahrscheinlich nicht richtig konfiguriert. Tatsächlich ist es sehr wahrscheinlich, dass das Modell dieselben HP-, Schadens-, Heilungs- und Bereichswerte in die Tabelle der Entscheidungsvariablen schreibt.

Und wir möchten natürlich, dass jede Klasse ihre eigene Persönlichkeit hat. Wir brauchen Krieger, um den größten Schaden zu verursachen, Magier haben die größte Reichweite, Heiler haben den maximalen Heilungswert und Barbaren haben die höchsten HP. Wir möchten auch, dass diese Unterschiede nicht zu klein sind - wir brauchen, dass sich diese Klassen stark voneinander unterscheiden.

Zu diesem Zweck erstellen wir eine kleine Tabelle mit Einschränkungen. Diese Tabelle stellt sicher, dass jede der vier Klassen ein entsprechendes Attribut hat, und gibt dann eine Bewertung von 0 oder 1, je nachdem, ob die Einschränkungsbedingung erfüllt ist.


Die Tabelle Min. Differenz rechts zeigt die minimale Differenz jedes Attributs der Klasse zu allen anderen Klassen. Mit anderen Worten, Krieger müssen mindestens 4 HP mehr Schaden haben als alle anderen Klassen, Magier müssen eine Angriffsreichweite von mindestens 10 mehr haben und so weiter.

Nachdem wir diese speziellen Einschränkungen hinzugefügt haben, ist es Zeit zu optimieren!

Suche nach Lösungen

Jetzt können wir das in Excel integrierte Solver-Tool („Finding Solutions“) ausführen, um zu versuchen, die Anfangsparameter zu optimieren. Als Zielzelle wählen wir die Score-Zelle aus, in der die Ergebnisse aller sechs Turniere zusammengefasst sind. Wir setzen die Entscheidungsvariablen so, dass alle 16 Zellen in der gelben Tabelle der Entscheidungsvariablen enthalten sind, die wir zu Beginn erstellt haben.

Wir legen die Einschränkungen (im Feld Betreff der Einschränkungen) wie folgt fest:

• Alle Entscheidungszellen müssen eine Ganzzahl mit einem Mindestwert von 0 sein.
• Alle Zellen in der HP-Spalte müssen einen Maximalwert von 200 und einen Minimalwert von 30 haben.
• Alle Zellen in der Spalte Schaden haben einen Maximalwert von 20.
• Alle Zellen in der Spalte Heilung haben einen Maximalwert von 15.
• Alle Zellen in der Spalte Bereich haben einen Maximalwert von 100.
• Außerdem müssen alle vier Zellen im Abschnitt "Spezielle Einschränkungen" auf 1 gesetzt werden, um ihre speziellen Bedingungen zu erfüllen.

Stellen Sie abschließend die Lösungsmethode auf Evolutionär ein und führen Sie Solver aus. Da es sich um einen evolutionären Algorithmus handelt, besteht die Möglichkeit, die während des zweiten oder dritten Solver-Laufs oder nach dem Einstellen von Parametern (Schaltfläche Optionen) für die evolutionäre Optimierung gefundene Lösung zu verbessern.

Als Ergebnis sollten wir etwas Ähnliches bekommen:


... und wie von Zauberhand gab uns Solver eine gute anfängliche Balance-Konfiguration.

Wie Sie sehen können, verursacht Krieger jetzt den größten Schaden, Magier hat die größte Reichweite, Heiler heilt am besten und Barbar hat die meisten HP. Darüber hinaus können Sie zu den Ergebnissen einzelner Turniere „Klasse gegen Klasse“ gehen und sehen, wie sich die Klassen im Kampf miteinander gezeigt haben. Wie Sie sehen können, sind die meisten von ihnen sehr gleichmäßig ausgeglichen - am Ende des Kampfes sterben beide Klassen oder eine von ihnen überlebt kaum. Außerdem dauern alle Turniere lange genug, und keine der Klassen kann die andere „wanhot“.

Nicht schlecht für ein paar Stunden Arbeit, oder?

Fazit

In diesem Beispiel haben wir eine einfache Auswuchtaufgabe erstellt und gezeigt, dass wir sie tatsächlich mithilfe von Simulation und Optimierung lösen können. Obwohl es offensichtlich ist, dass dies ein einfaches Beispiel ist, zeigt es uns die Leistungsfähigkeit von Modellierungstechniken und Entscheidungsoptimierung. Darüber hinaus kann es zu einer Inspirationsquelle werden, die in komplexeren Balancing-Tools verwendet werden kann, die eng in die Simulation des Spiels integriert sind. Wir hoffen, dass Sie dieses Beispiel als Leitfaden für die praktische Formulierung solcher Aufgaben verwenden können.

In den nächsten beiden Teilen der Serie werden wir uns mit dem Bereich der Zuweisungsaufgaben befassen, der mit der Auswahl optimaler Zuweisungen aus zwei oder mehr Gruppen von Entitäten verbunden ist. Wir werden zeigen, wie diese Art von Problemen gelöst werden können, und zeigen, wie wir diesen Ansatz verwendet haben, um das Turmdesign in unserem Strategiespiel für iOS / Android City Conquest zu erstellen.