Ich las ein maßgebliches Buch über Handelsstrategien und schrieb meinen Handelsroboter. Zu meiner Überraschung bringt der Roboter nicht Millionen, auch wenn er virtuell handelt. Der Grund liegt auf der Hand: Ein Roboter muss wie ein Rennwagen „abgestimmt“ werden, um Parameter auszuwählen, die an einen bestimmten Markt und einen bestimmten Zeitraum angepasst sind.
Da der Roboter über genügend Einstellungen verfügt, werden alle möglichen Kombinationen auf der Suche nach der besten, zu zeitaufwändigen Aufgabe durchlaufen. Zu einer Zeit, als ich das Optimierungsproblem löste, fand ich keine vernünftige Wahl des Suchalgorithmus für den quasi-optimalen Vektor der Parameter des Handelsroboters. Daher habe ich beschlossen, mehrere Algorithmen unabhängig voneinander zu vergleichen ...
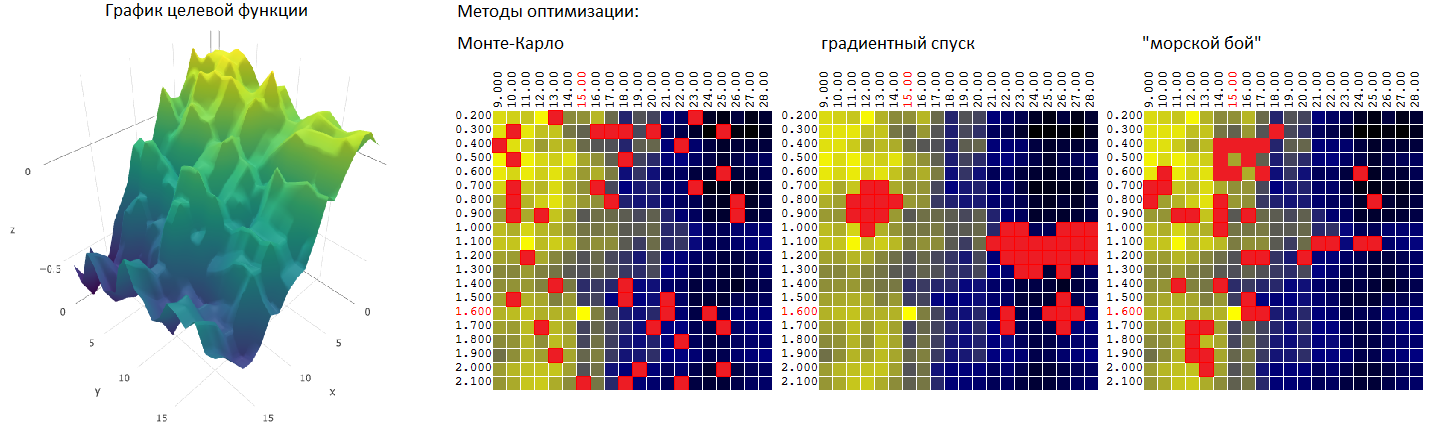
Kurze Darstellung des Optimierungsproblems
Wir haben einen Handelsalgorithmus. Eingabedaten - Preisverlauf des Stundenintervalls für 1 Beobachtungsjahr. Ausgabedaten - P - Gewinn oder Verlust, Skalarwert.
Der Handelsalgorithmus hat 4 konfigurierbare Parameter:
- Mf ist die Periode des "schnellen" gleitenden Durchschnitts ,
- Frau Periode des „langsamen“ gleitenden Durchschnitts
- T - TakeProfit, das Zielgewinnniveau für jede einzelne Transaktion,
- S - StopLoss, das Zielverlustniveau für jede einzelne Transaktion.
Wir weisen jedem Parameter einen Bereich und einen festen Änderungsschritt zu, insgesamt
20 Werte für jeden der Parameter.
Somit können wir nach dem maximalen Gewinn (P) für einen Parameter in einem Array von Eingabedaten suchen:
- Variieren eines Parameters, zum Beispiel P = f (Ms), Erzeugen von bis zu 20 Backtests ,
- Variieren von zwei Parametern, zum Beispiel P = f (Ms, T), was bis zu 20 * 20 = 400 Backtests ergibt,
- Variieren von drei Parametern, zum Beispiel P = f (Mf, Ms, T), was bis zu 20 * 20 * 20 = 8.000 Backtests ergibt,
- Variieren jedes der Parameter, P = f (Mf, Ms, T, S) und Erzeugen von bis zu 20 ^ 4 = 160.000 Backtests.
Bei den meisten Handelsalgorithmen dauert es jedoch mehrere Größenordnungen länger, einen einzelnen Test durchzuführen. Dies führt uns zu der Aufgabe, einen quasi optimalen Parametervektor zu finden, ohne den gesamten Satz möglicher Kombinationen durchlaufen zu müssen.
Details zum Handel und zu HandelsroboternHandel an der Börse, Wetten im Forex-Handelszentrum, verrückte Wetten auf „binäre Optionen“, Spekulationen mit Kryptowährungen - eine Art „Diagnose“ mit mehreren möglichen Optionen für die Entwicklung der „Krankheit“. Ein sehr häufiges Szenario ist, wenn ein Spieler nach dem Spielen von „Intuition“ zum automatischen Handel kommt. Versteh mich nicht falsch, ich möchte den Schwerpunkt nicht so legen, dass "technologisch und mathematisch" rigorose Handelsroboter dem naiven und hilflosen "manuellen" Handel entgegenstehen. Zum Beispiel bin ich selbst davon überzeugt, dass jeder meiner Versuche, durch Spekulationen, ob diskretionär oder vollautomatisch, Gewinn aus einem effizienten Markt (gelesen aus einem transparenten und liquiden Markt) zu ziehen, a priori zum Scheitern verurteilt ist. Wenn man vielleicht den Faktor des zufälligen Glücks nicht zulässt.
Der Handel und insbesondere der algo (rhythmische) Handel ist jedoch für viele ein beliebtes Hobby. Einige programmieren Handelsroboter unabhängig voneinander, andere gehen sogar noch weiter und erstellen ihre eigenen Plattformen zum Schreiben, Debuggen und Backtesting von Handelsstrategien, während andere einen vorgefertigten elektronischen „Experten“ herunterladen / kaufen. Aber auch diejenigen, die keine eigenen Handelsalgorithmen schreiben, sollten eine Vorstellung davon haben, wie sie mit dieser „Black Box“ umgehen sollen, um gemäß der Idee des Autors davon zu profitieren. Um nicht unbegründet zu sein, gebe ich meine weiteren Beobachtungen am Beispiel einer einfachen Handelsstrategie:
Einfacher Handelsroboter
Ein Handelsroboter analysiert die Dynamik des Goldwerts in Dollar pro Feinunze und beschließt, eine bestimmte Menge Gold zu „kaufen“ oder zu „verkaufen“. Der Einfachheit halber nehmen wir an, dass der Roboter immer mit einer Feinunze handelt.
Zum Zeitpunkt des Kaufs betrugen die Kosten für eine Feinunze Gold beispielsweise 1075,00
USD . Zum Zeitpunkt des anschließenden Verkaufs (Abschluss der Transaktion) stieg der Preis auf 1079,00 USD. Der Gewinn aus dieser Transaktion betrug 4 USD.
Wenn der Roboter Gold zu 1075,00 USD „verkauft“ und anschließend die Transaktion durch „Rückkauf“ von Gold zu einem Preis von 1079 USD abgeschlossen (abgeschlossen) hat, ist der Gewinn aus der Transaktion negativ - minus 4 USD. Eigentlich spielt es für uns keine Rolle, wie der Roboter Gold verkauft, das er nicht hat, um es später „zurückzukaufen“. Ein Broker / Handelszentrum ermöglicht es einem Händler, einen Vermögenswert auf die eine oder andere Weise zu „kaufen“ und zu „verkaufen“, wobei er aufgrund der unterschiedlichen Zinssätze verdient (oder häufiger verliert).
Wir haben uns für die
Eingabedaten für den Roboter entschieden - dies ist in der Tat die Zeitreihe der Goldpreise (Notierungen). Wenn Sie sagen, dass mein Beispiel zu einfach und nicht wichtig ist, kann ich Ihnen versichern: Die meisten Roboter, die auf dem Markt (und auch die Händler) in ihrem Handel zirkulieren, werden nur von der Preisstatistik der Waren geleitet, mit denen sie handeln. In jedem Fall gibt es beim Problem der parametrischen Optimierung einer Handelsstrategie keinen grundlegenden Unterschied zwischen einem Roboterhandel auf der Grundlage des Preisvektors und einem Roboter, der auf ein Terabyte-Array von mehrsortierten Marktanalysen zugreift. Die Hauptsache ist, dass beide Roboter anhand historischer Daten getestet werden können (sollten) können. Algorithmen müssen bestimmt werden: Das heißt, bei denselben Eingabedaten (Modellzeit, falls erforderlich, können wir sie auch als Parameter verwenden) sollte der Handelsroboter dasselbe Ergebnis anzeigen.
Weitere Details zum Handelsroboter finden Sie im folgenden Spoiler:
Roboter-Handelsalgorithmus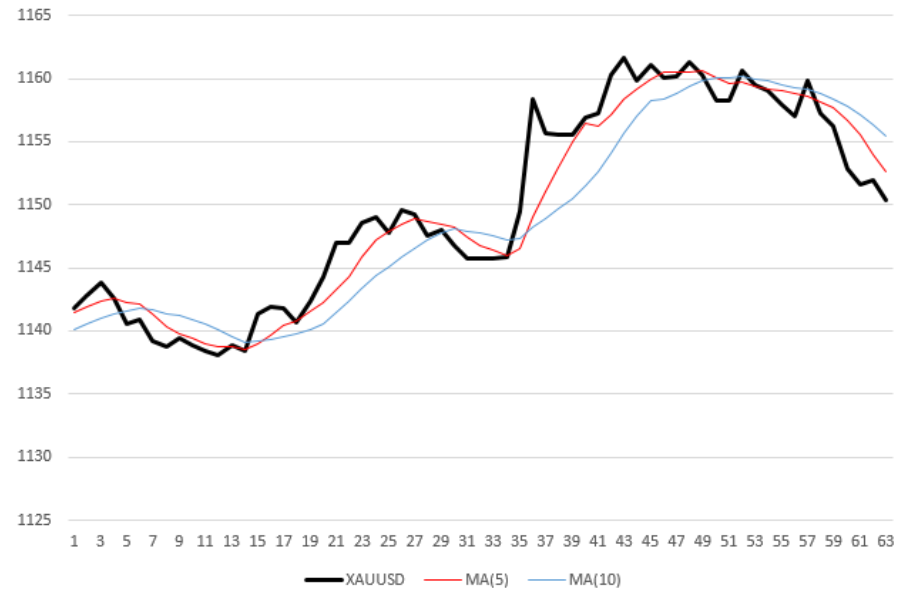
Die schwarze (dicke) Kurve auf dem Chart ist die stündliche
XAUUSD- Preismessung. Zwei dünne gestrichelte Linien, rot und blau - Durchschnittspreiswerte mit Durchschnittsperioden von 5 bzw. 10. Mit anderen Worten, gleitender Durchschnitt (Moving Average, MA) mit Perioden von 5, 10. Um beispielsweise die Ordinate des letzten (rechten) Punkts der roten Kurve zu berechnen, habe ich den Durchschnitt der letzten 5 Preiswerte genommen. Somit wird jeder gleitende Durchschnitt nicht nur relativ zur Preiskurve „geglättet“, sondern bleibt auch um die Hälfte seiner Periode relativ dazu zurück.
Regel zum Öffnen von Transaktionen
Der Roboter hat eine einfache Regel für eine Kauf- / Verkaufsentscheidung:
- Sobald ein gleitender Durchschnitt mit einer kurzen Periode („schnelle“
MA ) einen gleitenden Durchschnitt mit einer langen Periode („langsame“ MA) von unten nach oben überschreitet, kauft der Roboter einen Vermögenswert (Gold).
Sobald der „schnelle“ MA den „langsamen“ MA von oben nach unten kreuzt, verkauft der Roboter den Vermögenswert. In der obigen Abbildung führt der Roboter 5 Transaktionen durch: 3 Verkäufe zu den Zeitstempeln 7, 31 und 50 und zwei Käufe (Markierungen 16 und 36).
Der Roboter darf eine unbegrenzte Anzahl von Transaktionen öffnen. Zum Beispiel kann der Roboter irgendwann mehrere ausstehende Käufe und Verkäufe gleichzeitig haben.
Deal Closing Regel
Der Roboter schließt den Deal ab, sobald:
- Der Gewinn aus der Transaktion überschreitet den in Prozent angegebenen Schwellenwert - TakeProfit,
- oder der Verlust der Transaktion in Prozent übersteigt den entsprechenden Wert - StopLoss.
Angenommen, StopLoss beträgt 0,2%.
Der Deal ist ein "Verkauf" von Gold zu einem Preis von 1061,50.
Sobald der Goldpreis auf 1061,50 + 1061,50 * 0,2% / 100% = 1063,12% steigt, beträgt der Verlust aus dem Geschäft offensichtlich 0,2% und der Roboter schließt das Geschäft automatisch ab.
Der Roboter trifft alle Entscheidungen über das Öffnen / Schließen einer Transaktion zu diskreten Zeitpunkten - am Ende jeder Stunde nach Veröffentlichung des nächsten XAUUSD-Angebots.
Ja, der Roboter ist extrem einfach. Gleichzeitig erfüllt es zu 100% die Anforderungen dafür:
- Der Algorithmus ist deterministisch: Jedes Mal, wenn wir die Arbeit des Roboters mit denselben Preisdaten simulieren, erhalten wir dasselbe Ergebnis.
- hat eine ausreichende Anzahl einstellbarer Parameter, nämlich: die Periode des "schnellen" und die Periode des "langsamen" gleitenden Durchschnitts (natürliche Zahlen), TakeProfit und StopLoss - positive reelle Zahlen,
- Eine Änderung jedes der 4 Parameter wirkt sich im allgemeinen Fall nichtlinear auf die Handelseigenschaften des Roboters aus, insbesondere auf seine Rentabilität.
- Die Rentabilität eines Roboters in Bezug auf die Preisentwicklung wird als elementarer Programmcode betrachtet, und die Berechnung selbst dauert für einen Vektor von Tausenden von Anführungszeichen einen Sekundenbruchteil.
- Schließlich, was jedoch irrelevant ist, wird sich der Roboter mit all seiner Einfachheit in Wirklichkeit als nicht schlechter (wenn auch wahrscheinlich nicht besser) erweisen als der Gral, den der Autor im Internet für eine unbescheidene Menge verkauft.
Schnelle Suche nach einem quasi optimalen Satz von Eingabeparametern
Am Beispiel unseres einfachen Roboters ist ersichtlich, dass eine vollständige Aufzählung aller möglichen Vektoren der Robotereinstellungen selbst für 4 variable Parameter zu teuer ist. Eine offensichtliche Alternative zur umfassenden Suche ist die Auswahl von Parametervektoren für eine bestimmte Strategie. Wir betrachten nur einen Teil aller möglichen Kombinationen auf der Suche nach der besten, bei der sich die
CF der höchsten nähert (oder der kleinsten, je nachdem, welche CF wir wählen und welches Ergebnis wir erzielen).
Wir werden drei Suchalgorithmen für den quasi-
optimalen Wert des
digitalen Filters betrachten . Für jeden Algorithmus legen wir ein Limit von 40 Tests fest (von 400 möglichen Kombinationen).
Monte-Carlo-Methode
oder eine zufällige Auswahl von M unkorrelierten Vektoren aus der möglichen Anzahl von Sätzen gleich N. Das Verfahren ist wahrscheinlich das einfachste, das möglich ist. Wir werden es als Ausgangspunkt für den anschließenden Vergleich mit anderen Optimierungsmethoden verwenden.
Beispiel 1
Die Grafik zeigt die Abhängigkeit des Gewinns (P) unseres Handelsroboters
EURUSD , der vom jährlichen Segment der Geschichte der stündlichen Preismessungen erhalten wird, vom Parameterwert - der Periode des „langsamen“
gleitenden Durchschnitts (M). Alle anderen Parameter sind fest und nicht optimiert.
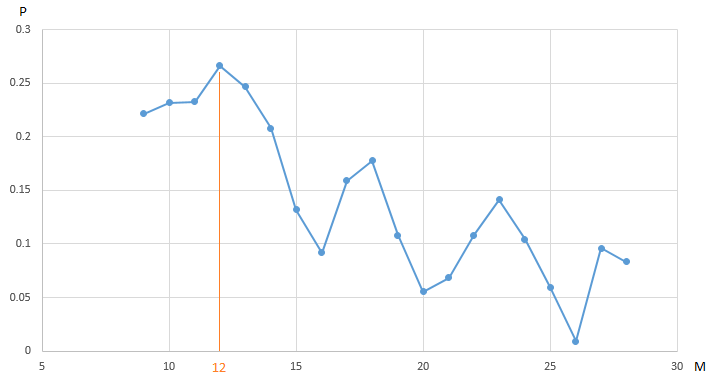
CF (Gewinn) erreicht am Punkt M = 12 ein Maximum von 0,27. Um den maximalen Wert des Gewinns zu gewährleisten, müssen wir 20 Testiterationen durchführen. Eine Alternative besteht darin, eine geringere Anzahl von Tests eines Handelsroboters mit einem zufällig ausgewählten Wert des Parameters M im Intervall durchzuführen [9, 20]. Zum Beispiel fanden wir nach 5 Iterationen (20% der Gesamtzahl der Tests einen quasi optimalen Vektor (Vektor offensichtlich eindimensional) von Parametern: M = 18 mit einem Wert von CF (M) gleich 0,18:

Die verbleibenden Werte in der Grafik unseres Optimierungsalgorithmus wurden vom „Nebel des Krieges“ verdeckt.
Durch die Optimierung eines der vier Parameter unseres Handelsroboters mit festen Werten der verbleibenden Parameter können wir nicht das gesamte Bild sehen. Vielleicht ist ein Maximum von 0,27 CF nicht der beste Wert des Indikators, wenn Sie den Wert anderer Parameter variieren?

Auf diese Weise ändert sich die Abhängigkeit des Gewinns von der Periode des gleitenden Durchschnitts für verschiedene Werte des TakeProfit-Parameters im Intervall [0,2 ... 0,8].
Monte-Carlo-Methode: Optimierung zweier Parameter
Die Abhängigkeit des Gewinns eines Handelsroboters von zwei Parametern kann grafisch als Oberfläche dargestellt werden:

Die beiden Achsen sind die Werte der Parameter T (TakeProfit) und M (Periode des gleitenden Durchschnitts), die dritte Achse ist der Gewinnwert.
Für unseren Handelsroboter erhalten wir nach 400 Tests in einem Datenintervall von einem Jahr (~ 6000 stündliche Notierungen des Euro gegenüber dem US-Dollar) eine Oberfläche des Formulars:

oder in der Ebene, in der die Werte der finanziellen Vermögenswerte (Gewinn, P) in Farbe dargestellt sind:

Bei der Auswahl beliebiger Punkte in der Ebene hat der Algorithmus in diesem Beispiel nicht den optimalen Wert gefunden, sondern ist ihm ziemlich nahe gekommen:

Wie effektiv ist die Monte-Carlo-Methode bei der Ermittlung der maximalen
CF ? Nachdem ich 1.000 Iterationen der Suche nach dem Maximum der CF für die Quelldaten aus dem obigen Beispiel durchgeführt hatte, erhielt ich die folgenden Statistiken:
- Der Durchschnittswert des Maximums des DF, der während 1.000 Optimierungsiterationen gefunden wurde (40 zufällige Vektoren von Parametern [M, T] aus 400 möglichen Kombinationen), betrug 0,231 oder 95,7% des globalen Maximums des DF (0,279).
Beim Vergleich der Methoden zur parametrischen Optimierung von Handelsrobotern ist eine Stichprobe offensichtlich kein Indikator. Diese Einschätzung reicht jedoch vorerst aus. Wir fahren mit der nächsten Methode fort - der
Gradientenabstiegsmethode .
Gradientenabstiegsmethode
Wie der Name schon sagt, wird die Methode formal verwendet, um nach dem Minimum des DF zu suchen.
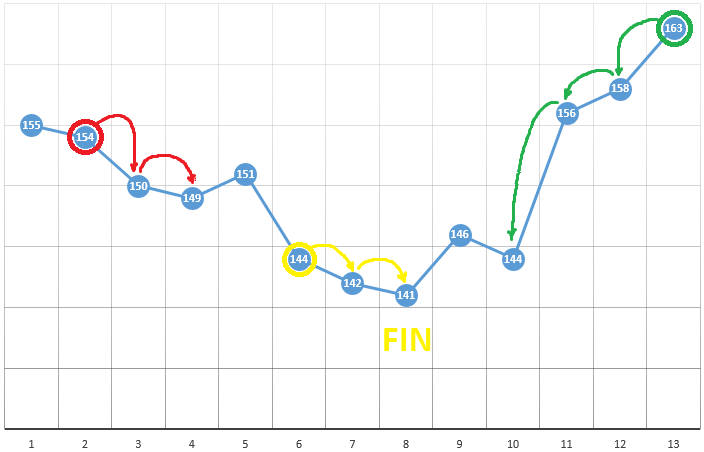
Entsprechend der Methode wählen wir den Startpunkt mit den Koordinaten [x0, y0, z0, ...]. Am Beispiel der Optimierung eines Parameters kann dies ein zufällig ausgewählter Punkt sein:
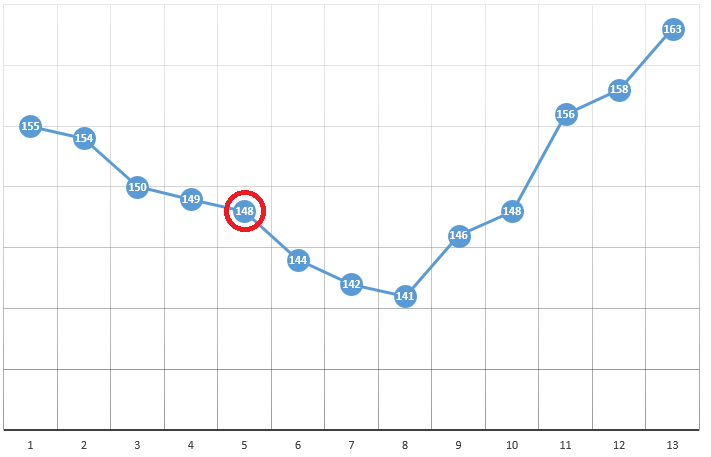
mit Koordinaten [5] und einem DF-Wert von 148. Es folgen drei einfache Schritte:
- Überprüfen Sie die CF-Werte in der Nähe der aktuellen Position (149 und 144).
- Bewegen Sie sich zu dem Punkt mit dem kleinsten CF-Wert
- Fehlt dies, wird ein lokales Extremum gefunden, der Algorithmus ist abgeschlossen

Um den DF in Abhängigkeit von zwei Parametern zu optimieren, verwenden wir denselben Algorithmus. Wenn früher, haben wir die CF an zwei benachbarten Punkten berechnet
Jetzt überprüfen wir 4 Punkte:
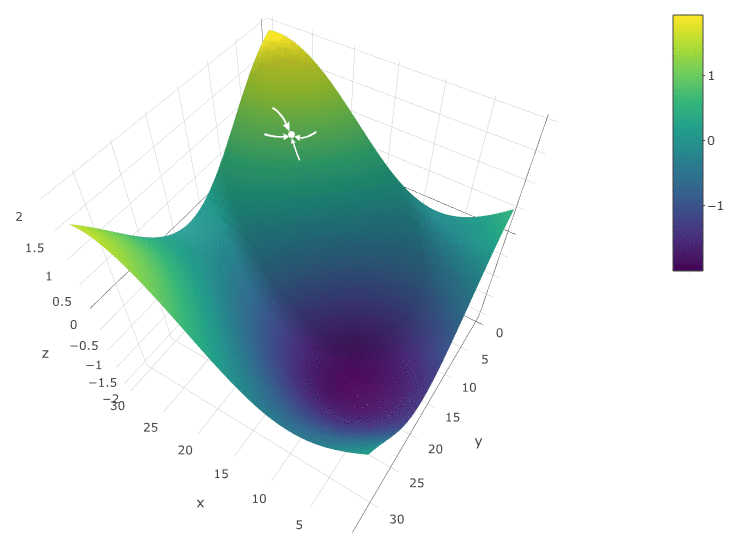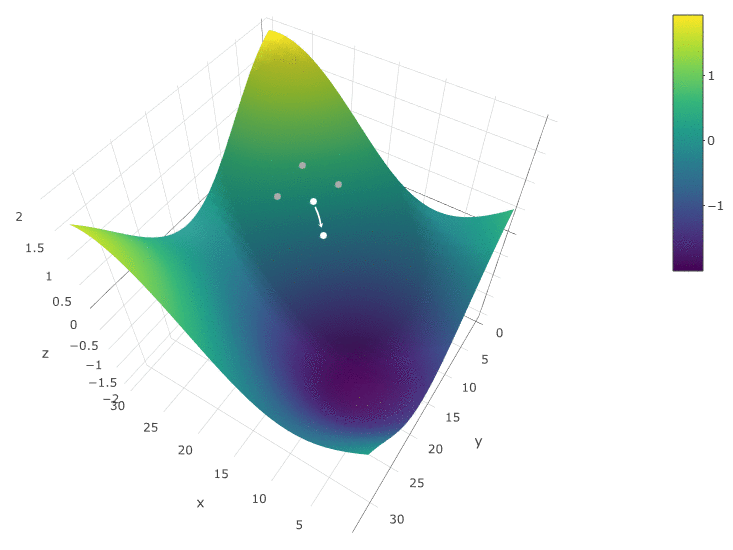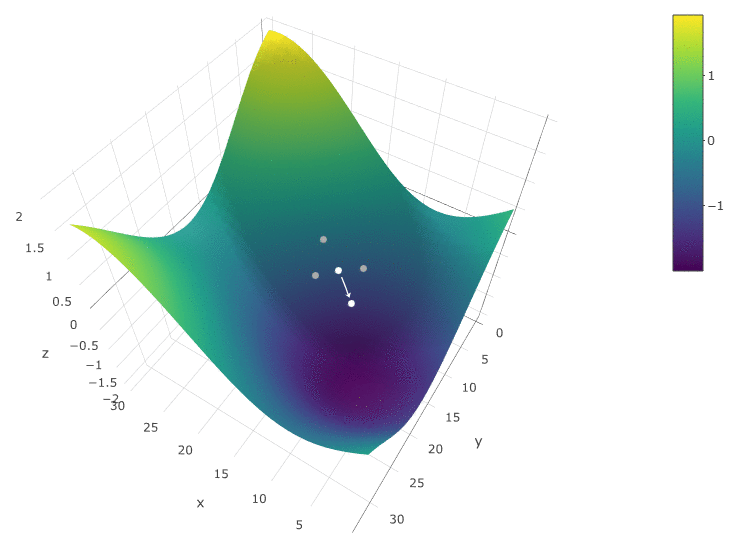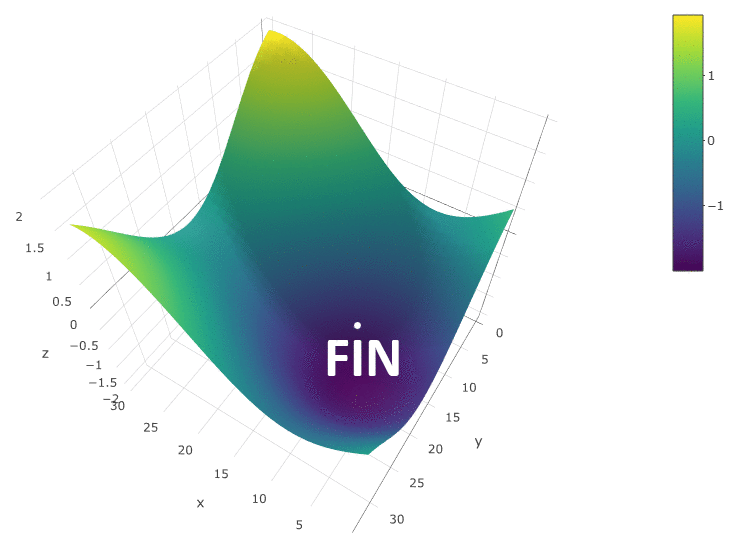
Die Methode ist definitiv gut, wenn es in einem DF in einem Testraum nur ein Extremum gibt. Wenn es mehrere Extrema gibt, muss die Suche mehrmals wiederholt werden, um die Wahrscheinlichkeit zu erhöhen, ein globales Extremum zu finden:
In unserem Beispiel suchen wir nach dem
maximalen DF. Um innerhalb der Definition des Algorithmus zu bleiben, können wir davon ausgehen, dass wir nach einem Minimum von „minus DF“ suchen. Trotzdem ist der Gewinn eines Handelsroboters in Abhängigkeit von der Periode des gleitenden Durchschnitts und dem TakeProfit-Wert eine Iteration:
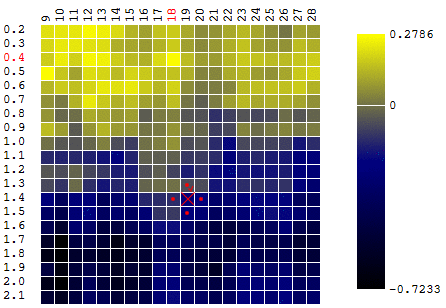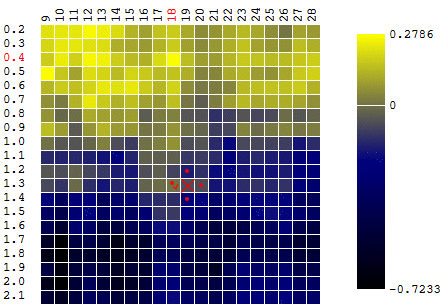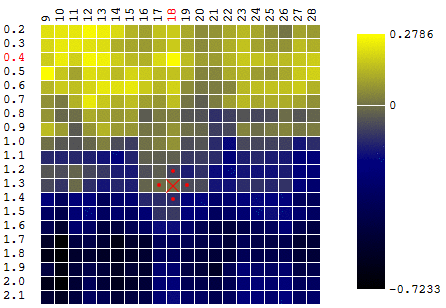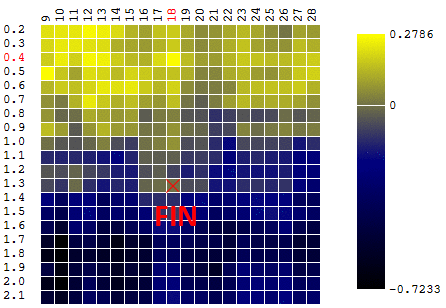
In diesem Fall wurde ein lokales Extremum gefunden, das weit vom globalen Maximum der CF entfernt ist. Als Beispiel für mehrere Iterationen der Suche nach dem Extremum des FS nach der Gradientenabstiegsmethode wird der Wert des FS 40-mal berechnet (40 von 400 möglichen Punkten):

Jetzt vergleichen wir die Effizienz der Suche nach dem globalen Maximum der CF (Gewinn) anhand unserer Anfangsdaten mithilfe von Monte-Carlo- und Gradientenabstiegsalgorithmen. Es werden jeweils 40 Tests durchgeführt (CF-Berechnungen). Mit jeder der Methoden wurden 1.000 Optimierungsiterationen durchgeführt:
| Monte Carlo | Gefälle Abstieg |
|---|
| der Durchschnitt des erhaltenen quasi-optimalen Wertes von CF. | 0,231 | 0,200 |
| der erhaltene Wert aus dem Maximum der CF. | 95,7% | 92,1% |
Wie Sie der Tabelle entnehmen können, ist in diesem Beispiel die Gradientenabstiegsmethode bei ihrer Aufgabe, das globale Extrem des digitalen Assets zu suchen, schlechter - der maximale Gewinn. Aber wir haben es nicht eilig, es wegzuwerfen.
Parametrische Stabilität des Handelsalgorithmus
Das Finden der Koordinaten des globalen Maximums / Minimums eines digitalen Filters ist oft kein Optimierungsziel. Angenommen, in der Grafik gibt es einen „scharfen“ Peak - ein globales Maximum, dessen Wert der CF in der Nähe viel niedriger ist als der Peakwert:
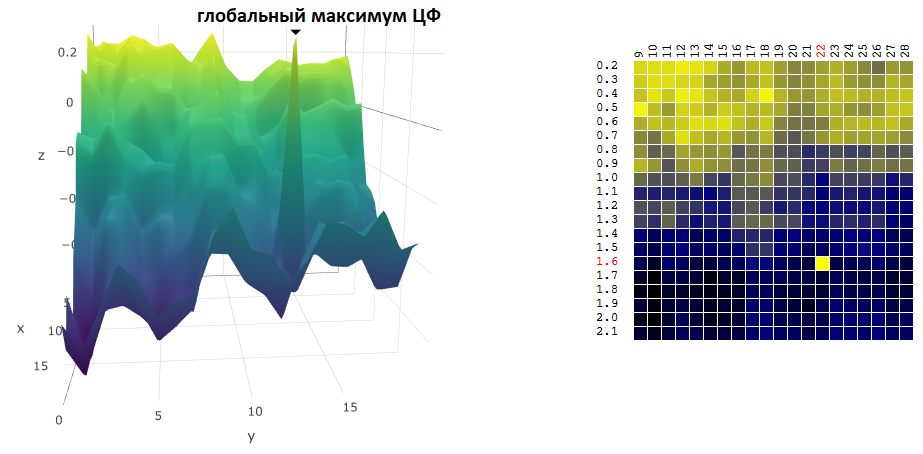
Angenommen, wir haben die Einstellungen des Handelsroboters ausgewählt, die dem gefundenen Maximum des digitalen Assets entsprechen. Sollten wir den Wert mindestens eines der Parameter - die Periode des gleitenden Durchschnitts und / oder TakeProfit - geringfügig ändern, sinkt die Rentabilität des Roboters stark (wird negativ). In Bezug auf den realen Handel kann man zumindest erwarten, dass sich der Markt, auf dem unser Roboter handeln soll, deutlich von dem Zeitraum unterscheidet, in dem wir den Handelsalgorithmus optimiert haben.
Wenn Sie die „optimalen“ Einstellungen eines Handelsroboters auswählen, sollten Sie sich daher ein Bild davon machen, wie empfindlich der Roboter auf Änderungen der Einstellungen in der Nähe des gefundenen Extrempunkts des DF reagiert.
Offensichtlich liefert die Gradientenabstiegsmethode in der Regel die Werte von TF in der Nähe des Extremums. Die Monte-Carlo-Methode trifft eher Quadrate.
In mehreren Anweisungen zum Testen automatisierter Handelsstrategien wird empfohlen, nach Abschluss der Optimierung die Zielindikatoren des Roboters in der Nähe des gefundenen Parametervektors zu überprüfen. Dies sind jedoch zusätzliche Tests. Was ist außerdem, wenn die Rentabilität der Strategie mit einer geringfügigen Änderung der Einstellungen sinkt? Natürlich müssen Sie den Testvorgang wiederholen.
Ein Algorithmus wäre für uns nützlich, der es uns gleichzeitig mit der Suche nach dem Extremum der CF ermöglichen würde, die Stabilität der Handelsstrategie zu bewerten, um Einstellungen in einem engen Bereich in Bezug auf die gefundenen Peaks zu ändern. Suchen Sie beispielsweise nicht direkt nach der maximalen CF.
und den gewichteten Durchschnittswert, der die Nachbarwerte der Zielfunktion berücksichtigt, wobei das Gewicht umgekehrt proportional zum Abstand zum Nachbarwert ist (um zwei Parameter x, y und die Zielfunktion P zu optimieren):
Mit anderen Worten, wenn ein quasi-optimaler Parametervektor ausgewählt wird, bewertet der Algorithmus die "geglättete" Zielfunktion:
war ist geworden
ist geworden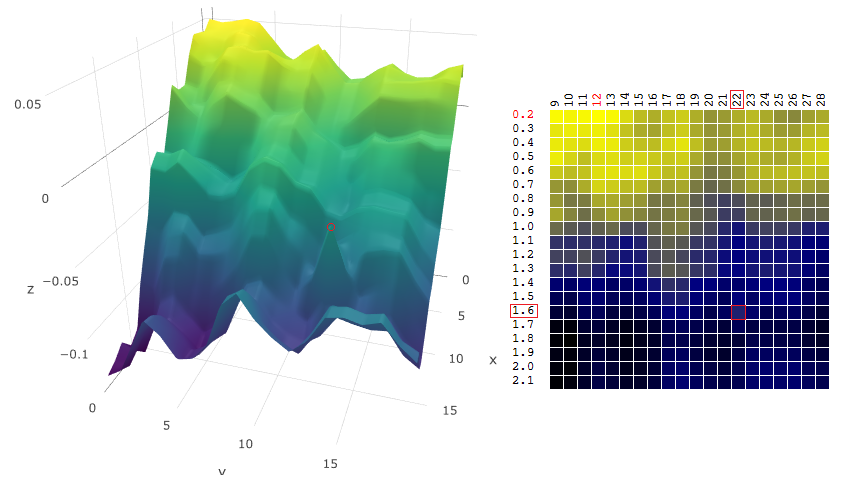
Die Methode der "Seeschlacht"
Um die Vorteile beider Methoden (Monte Carlo und Gradientenabstiegsmethode) zu kombinieren, habe ich einen Algorithmus ausprobiert, der dem Algorithmus des Spiels in der „Seeschlacht“ ähnelt:
- Zuerst schlage ich ein paar "Schläge" über den gesamten Bereich
- dann eröffne ich an Stellen mit „Treffern“ massives Feuer.
Mit anderen Worten werden die ersten N Tests an zufälligen unkorrelierten Vektoren von Eingabeparametern durchgeführt. Von diesen werden die M besten Ergebnisse ausgewählt. In der Nähe dieser Tests (plus - Minuten 0..L zu jeder der Koordinaten) werden weitere K-Tests durchgeführt.
Für unser Beispiel (400 Punkte, insgesamt 40 Versuche) haben wir:
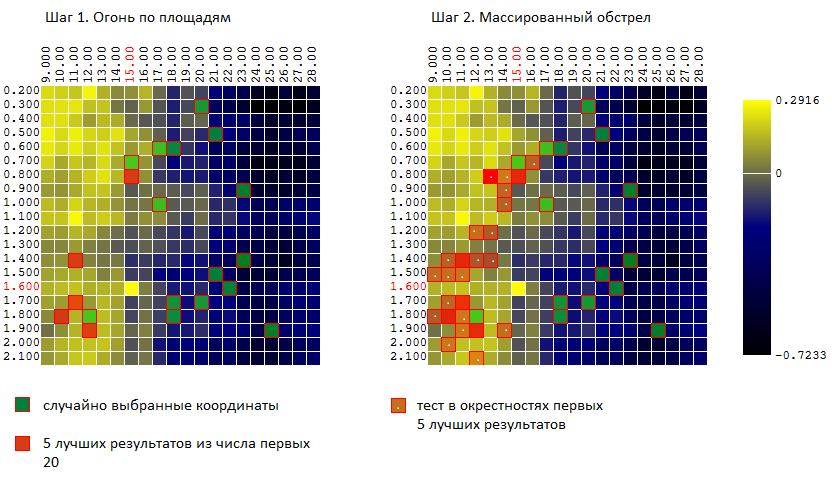
Und wieder vergleichen wir die Effektivität von jetzt 3 Optimierungsalgorithmen:
| Monte Carlo | Gefälle Abstieg | "Seeschlacht" |
|---|
Der Durchschnittswert des gefundenen Extremums der CF als Prozentsatz des globalen Werts.
40 Tests, 1.000 Optimierungsiterationen
| 95,7% | 92,1% | 97,0% |
Das Ergebnis ist ermutigend. Natürlich wurde der Vergleich an einer bestimmten Datenstichprobe durchgeführt: einem Handelsalgorithmus für eine Zeitreihe des Wertes des Euro gegenüber dem US-Dollar.
Bevor ich jedoch die Algorithmen für weitere Stichproben der Quelldaten vergleiche, werde ich auf einen anderen, unerwartet (ungerechtfertigt?) Beliebten Algorithmus zur Optimierung von Handelsstrategien eingehen - die Optimierung des genetischen Algorithmus (GA). Der Artikel erschien jedoch zu umfangreich, und die GA muss auf die nächste Veröffentlichung verschoben werden .