Einführung

OpenGL, das Backend für OpenSceneGraph, verwendet geometrische Grundelemente (wie Punkte, Linien, Dreiecke und polygonale Flächen), um alle Objekte in der dreidimensionalen Welt zu konstruieren.

Diese Grundelemente werden durch Daten über ihre Scheitelpunkte definiert, einschließlich der Koordinaten der Scheitelpunkte, Normalkomponenten, Farbdaten und Texturkoordinaten. Diese Daten werden in speziellen Arrays gespeichert. Grundelemente können beispielsweise gebildet werden, indem für die Objekte, die sie beschreiben, eine Liste von Scheitelpunktindizes angegeben wird. Diese Methode wird als Vertex-Array-Methode bezeichnet. Sie eliminiert die Speicherung redundanter Vertices im Speicher und weist eine gute Leistung auf.

Darüber hinaus kann OpenGL den Mechanismus sogenannter Anzeigelisten verwenden , wenn im Videospeicher vorbereitete Grundelemente wiederverwendet werden können, was die Anzeige statischer Objekte erheblich beschleunigt.

Standardmäßig verwendet OSG die Vertex-Array-Methode und die Anzeigelistenmethode, um die Geometrie zu rendern. Die Rendering-Strategie kann jedoch abhängig von der Darstellung der Geometriedaten geändert werden. In diesem Artikel werden die grundlegenden Techniken für die Arbeit mit Geometrie in OSG behandelt.

1. Klassen Geode und Drawable

Die osg :: Geode-Klasse ist ein Terminal, der sogenannte "Blatt" -Knoten des Szenenbaums. Es kann keine untergeordneten Knoten haben, enthält jedoch alle erforderlichen Informationen zum Rendern der Geometrie. Der Name Geode steht für Geometrieknoten.

Die von der Engine zu verarbeitenden geometrischen Daten werden in der Gruppe von Objekten der Klasse osg :: Drawable gespeichert, die von der Klasse osg :: Geode verwaltet wird. Die osg :: Drawable-Klasse ist eine rein virtuelle Klasse. Eine Reihe von Unterklassen werden davon geerbt, nämlich dreidimensionale Modelle, Bilder und Text, die von der OpenGL-Pipeline verarbeitet werden. OSG bezeichnet Drawable als alle Elemente, die von der Engine gezeichnet werden können.

Die Klasse osg :: Geode bietet eine Reihe von Methoden zum Anhängen und Trennen von Drawables:

• Öffentliche Methode addDrawable () - Übergibt einen Zeiger auf ein zeichnbares Element in einer Instanz der Klasse osg :: Geode. Alle diese Elemente werden von intelligenten Zeigern von osg :: ref_ptr <> gesteuert.
  
• Die öffentlichen Methoden removeDrawable () und removeDrawables () entfernen das Objekt aus osg :: Geode und verringern die Referenzanzahl dafür. Die Methode removeDrawable () verwendet als einzelnen Parameter einen Zeiger auf das interessierende Element, und die Methode removeDrawables () verwendet zwei Parameter: den Anfangsindex und die Anzahl der Elemente, die aus dem Objektarray osg :: Geode entfernt werden sollen.
  
• Die Methode getDrawable () gibt einen Zeiger auf ein Element am Index zurück, der als Parameter übergeben wird.
  
• Die Methode getNumDrawables () gibt die Gesamtzahl der an osg :: Geode angehängten Elemente zurück. Um beispielsweise alle Elemente aus osg :: Geode zu entfernen, können Sie solchen Code verwenden
  

geode->removeDrawables(0, geode->getNumDrawables()); 

2. Einfache Formen zeichnen

OSG stellt die Klasse osg :: ShapeDrawable bereit, die der Nachkomme der Klasse osg :: Drawable ist und zum Erstellen einfacher dreidimensionaler Grundelemente entwickelt wurde. Diese Klasse enthält ein osg :: Shape-Objekt, in dem Informationen zu bestimmten Geometrien und anderen Parametern gespeichert sind. Grundelemente werden beispielsweise mit der Methode setShape () generiert

 shapeDrawable->setShape(new osg::Box(osg::Vec3(1.0f, 0.0f, 0.0f), 10.0f, 10.0f, 5.0f)); 

Erstellt eine rechteckige Box mit einem geometrischen Mittelpunkt am Punkt (1.0, 0.0, 0.0) mit einer Breite und Höhe von 10 und einer Tiefe von 5 Einheiten. Die Klasse osg :: Vec3 definiert einen Vektor im dreidimensionalen Raum (zusätzlich werden auch die Klassen osg :: Vec2 und osg :: Vec4 dargestellt, die Vektoren der entsprechenden Dimension beschreiben).

Die beliebtesten Grundelemente werden in OSG durch die Klassen osg :: Box, osg :: Capsule, osg :: Cone, osg :: Cylinder und osg :: Sphere dargestellt.

Betrachten Sie ein Beispiel für die Anwendung dieses Mechanismus.

main.h

 #ifndef MAIN_H #define MAIN_H #include <osg/ShapeDrawable> #include <osg/Geode> #include <osgViewer/Viewer> #endif // MAIN_H 

main.cpp

 #include "main.h" int main(int argc, char *argv[]) { (void) argc; (void) argv; osg::ref_ptr<osg::ShapeDrawable> shape1 = new osg::ShapeDrawable; shape1->setShape(new osg::Box(osg::Vec3(-3.0f, 0.0f, 0.0f), 2.0f, 2.0f, 1.0f)); osg::ref_ptr<osg::ShapeDrawable> shape2 = new osg::ShapeDrawable; shape2->setShape(new osg::Cone(osg::Vec3(0.0f, 0.0f, 0.0f), 1.0f, 1.0f)); shape2->setColor(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f)); osg::ref_ptr<osg::ShapeDrawable> shape3 = new osg::ShapeDrawable; shape3->setShape(new osg::Sphere(osg::Vec3(3.0f, 0.0f, 0.0f), 1.0f)); shape3->setColor(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f)); osg::ref_ptr<osg::Geode> root = new osg::Geode; root->addDrawable(shape1.get()); root->addDrawable(shape2.get()); root->addDrawable(shape3.get()); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); } 

Dieses Beispiel benötigt insbesondere keine Kommentare: Im Programm werden drei einfache Formen erstellt, nach dem Kompilieren und Starten sehen wir ein solches Ergebnis



Der im Beispiel gezeigte Mechanismus ist einfach und unkompliziert, aber nicht die effektivste Methode zum Erstellen von Geometrie und kann ausschließlich für Tests verwendet werden. Die osg :: Geometry-Klasse wird zum Erstellen von Geometrie in leistungsstarken OSG-basierten Anwendungen verwendet.

3. Speicherung von Geometriedaten: Klassen osg :: Array und osg :: Geometry

Die osg :: Array-Klasse ist eine grundlegende abstrakte Klasse, von der mehrere Nachkommen geerbt werden, um Daten zu speichern, die an OpenGL-Funktionen übergeben werden. Die Arbeit mit dieser Klasse ähnelt der Arbeit mit std :: vector aus der C ++ - Standardbibliothek. Der folgende Code veranschaulicht das Hinzufügen eines Vektors zu einem Scheitelpunktarray mithilfe der push_back () -Methode

 vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f)); 

OSG-Arrays werden auf dem Heap zugewiesen und von intelligenten Zeigern verwaltet. Dies gilt jedoch nicht für Array-Elemente wie osg :: Vec3 oder osg :: Vec2, die auch auf dem Stapel erstellt werden können.

Die osg :: Geometry-Klasse ist ein Wrapper über OpenGL-Funktionen, die mit Vertex-Arrays arbeiten. Es ist von der Klasse osg :: Drawable abgeleitet und kann problemlos zur Objektliste osg :: Geode hinzugefügt werden. Diese Klasse verwendet die oben beschriebenen Arrays als Eingabe und verwendet sie zum Generieren von Geometrie mit OpenGL.

4. Eckpunkte und ihre Attribute

Ein Scheitelpunkt ist eine atomare Einheit von Geometrieprimitiven. Es hat eine Reihe von Attributen, die einen Punkt im zwei- oder dreidimensionalen Raum beschreiben. Zu den Attributen gehören: Position, Farbe, Normalvektor, Texturkoordinaten, Nebelkoordinaten usw. Die Oberseite muss immer eine Position im Raum haben, da andere Attribute optional vorhanden sein können. OpenGL unterstützt 16 grundlegende Scheitelpunktattribute und kann verschiedene Arrays zum Speichern verwenden. Alle Attribut-Arrays werden von der Klasse osg :: Geometry unterstützt und können mit Methoden des Formularsatzes * Array () festgelegt werden.

Scheitelpunktattribute in OpenSceneGraph

Attribut	Datentyp	Osg :: Geometry-Methode	Äquivalenter OpenGL-Aufruf
Position	3-Vektor	setVertexArray ()	glVertexPointer ()
Normal	3-Vektor	setNormalArray ()	glNormalPointer ()
Farbe	4-Vektor	setColorArray ()	glColorPointer ()
Sekundärfarbe	4-Vektor	setSecondaryColorArray ()	glSecondaryColorPointerEXT ()
Nebelkoordinaten	float	setFogCoordArray ()	glFogCoordPointerEXT ()
Texturkoordinaten	2- oder 3-Vektor	setTexCoordArray ()	glTexCoordPointer ()
Andere Attribute	Benutzerdefiniert	setVertexArribArray ()	glVertexAttribPointerARB ()

Grundsätzlich ist es erforderlich, für jeden Scheitelpunkt eigene Attribute festzulegen, was zur Bildung mehrerer Arrays von Attributen gleicher Größe führt. Andernfalls kann eine Nichtübereinstimmung der Größe der Arrays zu einem undefinierten Verhalten der Engine führen. OSG unterstützt beispielsweise verschiedene Methoden zum Verknüpfen von Scheitelpunktattributen

 geom->setColorBinding(osg::Geometry::BIND_PER_VERTEX); 

bedeutet, dass jeder Scheitelpunkt und jede Farbe des Scheitelpunkts eins zu eins miteinander korreliert ist. Wenn Sie sich jedoch einen solchen Code ansehen

 geom->setColorBinding(osg::Geometry::BIND_OVERALL); 

dann wendet er eine Farbe auf die gesamte Geometrie an. In ähnlicher Weise können Beziehungen zwischen anderen Attributen durch Aufrufen der Methoden setNormalBinding (), setSecondaryColorBinding (), setFogCoordBinding () und setVertexAttribBinding () konfiguriert werden.

5. Sätze von Geometrieprimitiven

Der nächste Schritt nach dem Definieren der Vertex-Attribut-Arrays besteht darin, zu beschreiben, wie die Vertex-Daten gerendert werden. Die virtuelle osg :: PrimitiveSet-Klasse wird verwendet, um die vom Renderer generierten geometrischen Grundelemente aus einer Reihe von Scheitelpunkten zu steuern. Die Klasse osg :: Geometry bietet verschiedene Methoden zum Arbeiten mit Sätzen von Geometrieprimitiven:

• addPrimitiveSet () - Übergibt einen Zeiger auf eine Reihe von Grundelementen in einem osg :: Geometry-Objekt.
  
• removePrimitiveSet () - entfernt eine Reihe von Grundelementen. Als Parameter werden der Anfangsindex der Sätze und die Anzahl der zu löschenden Sätze verwendet.
  
• getPrimitiveSet () - gibt eine Reihe von Grundelementen an dem als Parameter übergebenen Index zurück.
  
• getNumPrimitiveSets () - Gibt die Gesamtzahl der Sätze von Grundelementen zurück, die dieser Geometrie zugeordnet sind.
  

Die osg :: PrimitiveSet-Klasse ist abstrakt und kann nicht instanziiert werden, aber mehrere abgeleitete Klassen, die Sätze von Grundelementen enthalten, mit denen OpenGL arbeitet, wie z. B. osg :: DrawArrays und osg :: DrawElementsUInt, erben davon.

Die Klasse osg :: DrawArrays verwendet mehrere aufeinanderfolgende Elemente eines Scheitelpunktarrays, um ein geometrisches Grundelement zu erstellen. Es kann durch Aufrufen einer Methode erstellt und an die Geometrie angehängt werden.

 geom->addPrimitiveSet(new osg::DrawArrays(mode, first, count)); 

Der erste Parametermodus setzt den Primitivtyp auf die entsprechenden OpenGL-Primitivtypen: GL_POINTS, GL_LINE_STRIP, GL_LINE_LOOP, GL_LINES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES, GL_QUAD_STRIP, GL_QUADY und GL_.

Der erste und der zweite Parameter geben den ersten Index im Scheitelpunktarray und die Anzahl der Scheitelpunkte an, aus denen die Geometrie generiert werden soll. Darüber hinaus prüft OSG nicht, ob die angegebene Anzahl von Scheitelpunkten ausreicht, um die im Modus angegebene Geometrie zu erstellen, was zum Absturz der Anwendung führen kann!

6. Beispiel - Zeichnen Sie ein gemaltes Quadrat

Wir implementieren all das als einfaches Beispiel


Nach der Kompilierung und Ausführung erhalten wir ein ähnliches Ergebnis



Dieses Beispiel muss geklärt werden. Zunächst erstellen wir ein Array von Eckpunkten des Quadrats, in denen ihre Koordinaten gespeichert sind

 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array; vertices->push_back(osg::Vec3(0.0f, 0.0f, 0.0f)); vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f)); vertices->push_back(osg::Vec3(1.0f, 0.0f, 1.0f)); vertices->push_back(osg::Vec3(0.0f, 0.0f, 1.0f)); 

Als nächstes setzen wir das Array von Normalen. In unserem einfachen Fall müssen wir nicht für jeden Scheitelpunkt eine Normale erstellen - beschreiben Sie einfach einen Einheitsvektor, der senkrecht zur Ebene des Quadrats gerichtet ist

 osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array; normals->push_back(osg::Vec3(0.0f, -1.0f, 0.0f)); 

Legen Sie für jeden Scheitelpunkt eine Farbe fest

 osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array; colors->push_back(osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f)); colors->push_back(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f)); colors->push_back(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f)); colors->push_back(osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f)); 

Erstellen Sie nun ein Geometrieobjekt, in dem die Beschreibung unseres Quadrats gespeichert wird, das vom Render verarbeitet wird. Wir übergeben dieser Geometrie eine Reihe von Eckpunkten

 osg::ref_ptr<osg::Geometry> quad = new osg::Geometry; quad->setVertexArray(vertices.get()); 

Wenn wir ein Array von Normalen übergeben, informieren wir die Engine, dass eine einzige Normalen für alle Scheitelpunkte verwendet werden, indem wir die Bindungsmethode ("Bindung") der Normalen BIND_OVAERALL angeben

 quad->setNormalArray(normals.get()); quad->setNormalBinding(osg::Geometry::BIND_OVERALL); 

Wenn wir dagegen die Farben der Scheitelpunkte übergeben, geben wir an, dass jeder Scheitelpunkt seine eigene Farbe hat

 quad->setColorArray(colors.get()); quad->setColorBinding(osg::Geometry::BIND_PER_VERTEX); 

Erstellen Sie nun eine Reihe von Grundelementen für die Geometrie. Wir geben an, dass quadratische (GL_QUADS) Flächen aus dem Scheitelpunktarray generiert werden sollten, wobei der Scheitelpunkt mit dem Index 0 als erstem Scheitelpunkt verwendet wird und die Gesamtzahl der Scheitelpunkte 4 beträgt

 quad->addPrimitiveSet(new osg::DrawArrays(GL_QUADS, 0, 4)); 

Ich denke, es lohnt sich nicht, die Übertragung der Geometrie und den Start des Renderings zu erklären

 osg::ref_ptr<osg::Geode> root = new osg::Geode; root->addDrawable(quad.get()); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); 

Der obige Code entspricht dem folgenden Design in reinem OpenGL

 static const GLfloat vertices[][3] = { … }; glEnableClientState( GL_VERTEX_ARRAY ); glVertexPointer( 4, GL_FLOAT, 0, vertices ); glDrawArrays( GL_QUADS, 0, 4 ); 

7. Indizieren von Eckpunkten in Grundelementen

Die osg :: DrawArrays-Klasse funktioniert gut, wenn Scheitelpunktdaten ohne Lücken direkt aus Arrays gelesen werden. Dies ist jedoch nicht so effektiv, wenn derselbe Scheitelpunkt zu mehreren Flächen eines Objekts gehören kann. Schauen wir uns ein Beispiel an.



Der Würfel hat acht Eckpunkte. Wie aus der Abbildung ersichtlich ist (wir betrachten die Entfaltung des Würfels in der Ebene), gehören einige Scheitelpunkte zu mehr als einer Fläche. Wenn Sie einen Würfel mit 12 dreieckigen Flächen erstellen, werden diese Scheitelpunkte wiederholt, und anstelle eines Arrays mit 8 Scheitelpunkten erhalten wir ein Array mit 36 ​​Scheitelpunkten, von denen die meisten tatsächlich der gleiche Scheitelpunkt sind!

Die OSG-Klassen osg :: DrawElementsUInt, osg :: DrawElementsUByte und osg :: DrawElementsUShort, die Vertex-Index-Arrays als Daten verwenden, sollen das beschriebene Problem lösen. Arrays von Indizes speichern Indizes von Eckpunkten von Grundelementen, die Flächen und andere Elemente der Geometrie beschreiben. Wenn Sie diese Klassen für einen Cube anwenden, ist es ausreichend, ein Array von acht Scheitelpunkten zu speichern, die Flächen durch Arrays von Indizes zugeordnet sind.

Klassen vom Typ osg :: DrawElements * werden auf die gleiche Weise wie die Standardklasse std :: vector erstellt. Mit diesem Code können Indizes hinzugefügt werden.

 osg::ref_ptr<osg::DrawElementsUInt> de = new osg::DrawElementsUInt(GL_TRIANGLES); de->push_back(0); de->push_back(1); de->push_back(2); de->push_back(3); de->push_back(0); de->push_back(2); 

Dieser Code definiert die Vorderseite des in der Abbildung gezeigten Würfels.

Betrachten wir ein weiteres anschauliches Beispiel - ein Oktaeder



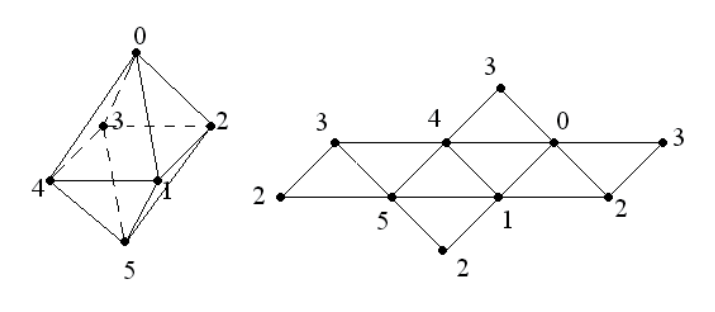
Es ist interessant, weil es nur sechs Eckpunkte enthält, aber jeder Eckpunkt bis zu vier dreieckige Flächen eingibt! Mit osg :: DrawArrays können wir ein Array mit 24 Scheitelpunkten erstellen, um alle acht Flächen anzuzeigen. Wir werden jedoch etwas anderes tun - wir werden die Eckpunkte in einem Array von sechs Elementen speichern und Gesichter mit der Klasse osg :: DrawElementsUInt generieren.


Lassen Sie uns diesen Code genauer analysieren. Als erstes erstellen wir natürlich ein Array mit sechs Eckpunkten

 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array(6); (*vertices)[0].set( 0.0f, 0.0f, 1.0f); (*vertices)[1].set(-0.5f, -0.5f, 0.0f); (*vertices)[2].set( 0.5f, -0.5f, 0.0f); (*vertices)[3].set( 0.5f, 0.5f, 0.0f); (*vertices)[4].set(-0.5f, 0.5f, 0.0f); (*vertices)[5].set( 0.0f, 0.0f, -1.0f); 

Wir initialisieren jeden Scheitelpunkt direkt, indem wir mit der Dereferenzierungsoperation des Zeiger- und Operatoroperators [] auf den Vektor seiner Koordinaten zugreifen (wir erinnern uns, dass osg :: Array in seinem Gerät std :: vector ähnlich ist).

Erstellen Sie nun Flächen als Liste von Scheitelpunktindizes

 osg::ref_ptr<osg::DrawElementsUInt> indices = new osg::DrawElementsUInt(GL_TRIANGLES, 24); (*indices)[ 0] = 0; (*indices)[ 1] = 1; (*indices)[ 2] = 2; //  0 (*indices)[ 3] = 0; (*indices)[ 4] = 4; (*indices)[ 5] = 1; //  1 (*indices)[ 6] = 4; (*indices)[ 7] = 5; (*indices)[ 8] = 1; //  2 (*indices)[ 9] = 4; (*indices)[10] = 3; (*indices)[11] = 5; //  3 (*indices)[12] = 3; (*indices)[13] = 2; (*indices)[14] = 5; //  4 (*indices)[15] = 1; (*indices)[16] = 5; (*indices)[17] = 2; //  5 (*indices)[18] = 3; (*indices)[19] = 0; (*indices)[20] = 2; //  6 (*indices)[21] = 0; (*indices)[22] = 3; (*indices)[23] = 4; //  7 

Die Flächen sind dreieckig, es gibt 8, was bedeutet, dass die Liste der Indizes 24 Elemente enthalten sollte. Die Indizes von Flächen verlaufen in diesem Array nacheinander: Zum Beispiel wird die Fläche 0 durch die Eckpunkte 0, 1 und 2 gebildet; Fläche 1 - Eckpunkte 0, 4 und 1; Gesicht 2 - Eckpunkte 4, 5 und 1 und so weiter. Die Eckpunkte werden gegen den Uhrzeigersinn aufgelistet, wenn Sie das Gesicht des Gesichts betrachten (siehe Abbildung oben).

Weitere Schritte zum Erstellen der Geometrie haben wir in den vorherigen Beispielen ausgeführt. Das einzige, was wir nicht getan haben, war die automatische Erzeugung geglätteter (gemittelter) Normalen, die wir in diesem Beispiel durch Aufrufen ausführen

 osgUtil::SmoothingVisitor::smooth(*geom); 

In der Tat ist es einfach, die Normalen zu berechnen, wenn die Eckpunkte eines Gesichts angegeben sind. An den Eckpunkten, an denen mehrere Flächen zusammenlaufen, wird eine bestimmte durchschnittliche Normalen berechnet - die Normalen der konvergierenden Flächen werden addiert und die resultierende Summe erneut normalisiert. Diese Operationen (und vieles mehr!) Können von der Engine selbst mithilfe von Klassen aus der osgUtil-Bibliothek ausgeführt werden. Daher fügen wir in unserem Beispiel dem Linker eine Anweisung hinzu, um unser Programm mit dieser Bibliothek in der * .pro-Datei zu erstellen

octahedron.pro

 CONFIG(debug, debug|release) { TARGET = $$join(TARGET,,,_d) . . . LIBS += -L$$OSG_LIB_DIRECTORY -losgUtild } else { . . . LIBS += -L$$OSG_LIB_DIRECTORY -losgUtil } 

Als Ergebnis erhalten wir das folgende Ergebnis



Betrachten Sie die OpenGL-Pipeline, um zu verstehen, wie dies funktioniert



Der Vertex-Array-Mechanismus reduziert die Anzahl der OpenGL-Aufrufe. Es speichert Vertexdaten im Anwendungsspeicher, der auf der Clientseite verwendet wird. Die OpenGL-Pipeline auf der Serverseite erhält Zugriff auf verschiedene Vertex-Arrays. Wie im Diagramm gezeigt, empfängt OpenGL Daten vom Scheitelpunktpuffer auf der Clientseite und führt in geordneter Weise die Zusammenstellung von Grundelementen durch. Auf diese Weise werden Daten mit den set * Array () -Methoden der Klasse osg :: Geometry verarbeitet. Die Klasse osg :: DrawArrays durchläuft diese Arrays direkt und zeigt sie an.

Bei Verwendung von osg :: DrawElements * wird die Dimension von Scheitelpunktarrays verringert und die Anzahl der in die Pipeline übertragenen Scheitelpunkte verringert. Mit einem Array von Indizes können Sie einen Server-Cache mit Scheitelpunkten erstellen. OpenGL liest Scheitelpunktdaten aus dem Cache, anstatt aus dem Scheitelpunktpuffer auf der Clientseite zu lesen. Dies erhöht die allgemeine Renderleistung erheblich.

8. Polygonnetz-Verarbeitungstechniken

OpenSceneGraph unterstützt verschiedene Techniken zur Verarbeitung des Polygonnetzes von Szenengeometrieobjekten. Diese Vorverarbeitungsmethoden wie Polygonreduktion und Tessellation werden häufig verwendet, um polygonale Modelle zu erstellen und zu optimieren. Sie haben eine einfache Oberfläche, führen dabei jedoch viele komplexe Berechnungen durch und eignen sich nicht sehr gut für die sofortige Ausführung.

Die beschriebenen Techniken umfassen:

1. osgUtil :: Simplifier - Reduziert die Anzahl der Dreiecke in der Geometrie. Die öffentliche Methode simplify () wird verwendet, um die Modellgeometrie zu vereinfachen.
   
2. osgUtil :: SmootingVisitor - Berechnung von Normalen. Die Methode glatt () kann verwendet werden, um geglättete Normalen für das Modell zu generieren, anstatt sie unabhängig zu berechnen und explizit durch ein Array von Normalen zu setzen.
   
3. osgUtil :: TangentSpaceGenerator - Generierung von Tangentenbasisvektoren für Modellscheitelpunkte. Es wird durch Aufrufen der generate () -Methode gestartet und speichert das von den Methoden getTangentArray (), getNormalArray () und getBinormalArray () zurückgegebene Ergebnis. Diese Ergebnisse können für verschiedene Scheitelpunktattribute beim Schreiben von Shadern in GLSL verwendet werden.
   
4. osgUtil :: Tesselator - führt die Tessellierung eines Polygonnetzes durch - teilt komplexe Grundelemente in eine Folge einfacher Grundelemente auf (retesselatePolygons () -Methode)
   
5. osgUtil :: TriStripVisitor - konvertiert eine geometrische Oberfläche in einen Satz Streifen dreieckiger Flächen, wodurch das Rendern mit effizientem Speicherverbrauch ermöglicht wird. Die Methode stripify () konvertiert eine Reihe von Modellprimitiven basierend auf der Menge GL_TRIANGLE_STRIP in Geometrie.
   

Alle Methoden akzeptieren die Geometrie des Objekts als Parameter, der beispielsweise von osg :: Geometry & link übergeben wird

 osgUtil::TriStripVisitor tsv; tsv.stripify(*geom); 

Dabei bezieht sich Geom auf eine Geometrieinstanz, die durch einen intelligenten Zeiger beschrieben wird.

Die Klassen osg :: Simplifier, osg :: SmoothingVisitor und osg :: TriStripVisitor können beispielsweise direkt mit Knoten im Szenendiagramm arbeiten

 osgUtil::TriStripVisitor tsv; node->accept(tsv); 

Die Methode accept () verarbeitet alle untergeordneten Knoten, bis die angegebene Operation auf alle Endknoten dieses Teils des Szenenbaums angewendet wird, der in Knoten vom Typ osg :: Geode gespeichert ist.

Lassen Sie uns die Tessellationstechnik in der Praxis ausprobieren.


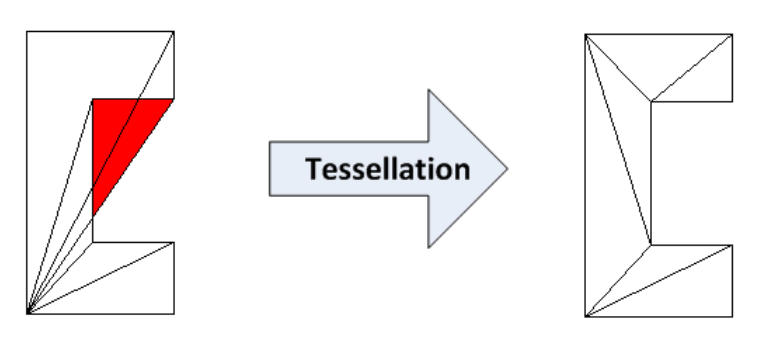
Anhand der räumlichen Position der Scheitelpunkte in diesem Beispiel wird deutlich, dass wir versuchen, ein nicht konvexes Polygon aus acht Scheitelpunkten zu erstellen, indem eine Fläche vom Typ GL_POLYGON generiert wird. Die Zusammenstellung und Ausführung dieses Beispiels zeigt, dass das erwartete Ergebnis nicht funktioniert - das Beispiel wird falsch angezeigt



Um dieses Problem zu beheben, muss die konstruierte Geometrie tesselliert werden, bevor sie an den Viewer übergeben wird

 osgUtil::Tessellator ts; ts.retessellatePolygons(*geom); 

Danach erhalten wir das richtige Ergebnis



Wie funktioniert es Ein nicht konvexes Polygon ohne die Verwendung einer korrekten Tessellation wird nicht wie erwartet angezeigt, da OpenGL, um die Leistung zu optimieren, es als einfaches, konvexes Polygon betrachtet oder es einfach ignoriert, was zu völlig unerwarteten Ergebnissen führen kann.

Die Klasse osgUtil :: Tessellator verwendet Algorithmen, um ein konvexes Polygon in eine Reihe nicht konvexer zu transformieren. In unserem Fall transformiert sie die Geometrie in GL_TRIANGLE_STRIP.



Diese Klasse kann Lochpolygone und sich selbst schneidende Polygone verarbeiten. Mit der öffentlichen Methode setWindingType () können Sie verschiedene Verarbeitungsregeln definieren, z. B. GLU_TESS_WINDING_ODD oder GLU_TESS_WINDING_NONZERO, die den inneren und äußeren Bereich eines komplexen Polygons angeben.

Fazit

In diesem Artikel haben wir ein grundlegendes Verständnis dafür erhalten, wie die Geometrie dreidimensionaler Objekte in der OSG-Engine gespeichert und verarbeitet wird. Denken Sie nicht, dass diese einfachen und nicht zu eindrucksvollen Beispiele, die in diesem Artikel behandelt werden, die Grenzen der Motorleistung darstellen. Nur diese Beispiele können dem Entwickler helfen, die Mechanik von OpenSceneGraph zu verstehen, und ohne dieses Verständnis ist es schwierig, sich die Arbeit komplexerer Dinge vorzustellen.

Dieser Artikel basiert auf der Übersetzung und Verarbeitung des Textes der entsprechenden Kapitel des Buches OpenSceneGraph 3.0. Anfängerleitfaden . Alle Beispiele werden von mir persönlich geprüft und ihr Quellcode ist hier verfügbar . Fortsetzung folgt...