Einführung

Wenn ein Punkt, eine Linie oder ein komplexes Polygon in einer dreidimensionalen Welt gezeichnet wird, wird das Endergebnis letztendlich auf einem flachen, zweidimensionalen Bildschirm angezeigt. Dementsprechend durchlaufen dreidimensionale Objekte einen bestimmten Transformationspfad und verwandeln sich in einen Satz von Pixeln, die in einem zweidimensionalen Fenster angezeigt werden.

Die Entwicklung von Softwaretools, die dreidimensionale Grafiken implementieren, hat unabhängig davon, welches Sie wählen, ungefähr das gleiche Konzept sowohl der mathematischen als auch der algorithmischen Beschreibung der obigen Transformationen erreicht. Ideologisch verwenden „saubere“ Grafik-APIs wie OpenGL und coole Game-Engines wie Unity und Unreal ähnliche Mechanismen zur Beschreibung der Transformation einer dreidimensionalen Szene. OpenSceneGraph ist keine Ausnahme.

In diesem Artikel werden die Mechanismen zum Gruppieren und Transformieren dreidimensionaler Objekte in OSG beschrieben.

1. Modellmatrix, Ansichtsmatrix und Projektionsmatrix

Drei Grundmatrizen, die an der Transformation von Koordinaten beteiligt sind, sind an der Transformation zwischen verschiedenen Koordinatensystemen beteiligt. In OpenGL-Begriffen werden sie häufig als Modellmatrix , Ansichtsmatrix und Projektionsmatrix bezeichnet .

Die Matrix des Modells wird verwendet, um die Position des Objekts in der 3D-Welt zu beschreiben. Es konvertiert Scheitelpunkte vom lokalen Koordinatensystem des Objekts in das Weltkoordinatensystem . Übrigens sind alle Koordinatensysteme in OSG Rechtshänder .

Der nächste Schritt ist die Transformation von Weltkoordinaten in einen Ansichtsraum, die unter Verwendung der Ansichtsmatrix durchgeführt wird. Angenommen, wir haben eine Kamera am Ursprung des Weltkoordinatensystems. Die zur Kameratransformationsmatrix inverse Matrix wird tatsächlich als Ansichtsmatrix verwendet. In einem rechtshändigen Koordinatensystem definiert OpenGL standardmäßig immer eine Kamera, die sich am Punkt (0, 0, 0) des globalen Koordinatensystems befindet und entlang der negativen Richtung der Z-Achse gerichtet ist.

Ich stelle fest, dass in OpenGL die Modellmatrix und die Ansichtsmatrix nicht getrennt sind. Dort wird jedoch die Modellansichtsmatrix bestimmt, die die lokalen Koordinaten des Objekts in die Koordinaten des Ansichtsraums umwandelt. Diese Matrix ist tatsächlich das Produkt der Modellmatrix und der Matrix der Form. Somit kann die Transformation eines Scheitelpunkts V von lokalen Koordinaten in einen Raum der Form bedingt als Produkt geschrieben werden

Ve = V * modelViewMatrix 

Die nächste wichtige Aufgabe besteht darin, zu bestimmen, wie 3D-Objekte auf die Bildschirmebene projiziert werden, und die sogenannte Schnittpyramide zu berechnen - einen Raumbereich, der Objekte enthält, die auf dem Bildschirm angezeigt werden sollen. Die Projektionsmatrix wird verwendet, um die im Weltraum durch sechs Ebenen definierte Schnittpyramide anzugeben: links, rechts, unten, oben, nah und fern. OpenGL bietet die Funktion gluPerapective (), mit der Sie eine Schnittpyramide angeben und eine dreidimensionale Welt auf eine Ebene projizieren können.

Das nach den obigen Transformationen erhaltene Koordinatensystem wird als normalisiertes Koordinatensystem des Geräts bezeichnet , hat auf jeder Achse einen Koordinatenbereich von -1 bis 1 und ist linkshändig. Als letzten Schritt werden die empfangenen Daten in den Anzeigeport (Ansichtsfenster) des Fensters projiziert, der durch das Rechteck des Clientbereichs des Fensters definiert ist. Danach erscheint die 3D-Welt auf unserem 2D-Bildschirm. Der Endwert der Bildschirmkoordinaten der Eckpunkte Vs kann durch die folgende Transformation ausgedrückt werden

 Vs = V * modelViewMatrix * projectionMatrix * windowMatrix 

oder

 Vs = V * MVPW 

Dabei ist MVPW die äquivalente Transformationsmatrix, die dem Produkt aus drei Matrizen entspricht: Modellansichtsmatrizen, Projektionsmatrizen und Fenstermatrizen.

Vs ist in dieser Situation ein dreidimensionaler Vektor, der die Position eines 2D-Pixels mit einem Tiefenwert bestimmt. Durch Invertieren der Koordinatentransformationsoperation erhalten wir eine Linie im dreidimensionalen Raum. Daher kann ein 2D-Punkt als zwei Punkte betrachtet werden - einer in der nahen (Zs = 0), der andere in der fernen Schnittebene (Zs = 1). Die Koordinaten dieser Punkte im dreidimensionalen Raum

 V0 = (Xs, Ys, 0) * invMVPW V1 = (Xs, Ys, 1) * invMVPW 

Dabei ist invMVPW die Umkehrung von MVPW.

In allen bisher diskutierten Beispielen haben wir ein einzelnes dreidimensionales Objekt in den Szenen erstellt. In diesen Beispielen stimmten die lokalen Koordinaten des Objekts immer mit den globalen globalen Koordinaten überein. Jetzt ist es Zeit, über Werkzeuge zu sprechen, mit denen Sie viele Objekte in der Szene platzieren und ihre Position im Raum ändern können.

2. Knoten gruppieren

Die osg :: Group-Klasse ist der sogenannte Gruppenknoten eines Szenendiagramms in OSG. Es kann eine beliebige Anzahl von untergeordneten Knoten haben, einschließlich Geometrieblattknoten oder anderer Gruppenknoten. Dies sind die am häufigsten verwendeten Knoten mit umfangreichen Funktionen.

Die Klasse osg :: Group wird von der Klasse osg :: Node abgeleitet und erbt dementsprechend von der Klasse osg :: Referenced. osg :: Group enthält eine Liste von untergeordneten Knoten, wobei jeder untergeordnete Knoten von einem intelligenten Zeiger gesteuert wird. Dies stellt sicher, dass beim Kaskadieren eines Zweigs eines Szenenbaums keine Speicherlecks auftreten. Diese Klasse bietet dem Entwickler eine Reihe öffentlicher Methoden.

1. addChild () - Hängt den Knoten an das Ende der Liste der untergeordneten Knoten an. Auf der anderen Seite gibt es die Methode insertChild (), mit der der untergeordnete Knoten an einer bestimmten Position in der Liste platziert wird, die durch einen ganzzahligen Index oder einen Zeiger auf den als Parameter übergebenen Knoten angegeben wird.
   
2. removeChild () und removeChildren () - Entfernen Sie einen einzelnen Knoten oder eine Gruppe von Knoten.
   
3. getChild () - Abrufen eines Zeigers auf einen Knoten anhand seines Index in der Liste
   
4. getNumChildren () - Ermittelt die Anzahl der untergeordneten Knoten, die dieser Gruppe zugeordnet sind.
   

Übergeordnete Knotenverwaltung

Wie wir bereits wissen, verwaltet die Klasse osg :: Group Gruppen ihrer untergeordneten Objekte, unter denen sich möglicherweise osg :: Geode-Instanzen befinden, die die Geometrie von Szenenobjekten steuern. Beide Klassen verfügen über eine Schnittstelle zum Verwalten übergeordneter Knoten.

Mit OSG können Szenenknoten mehrere übergeordnete Knoten haben (wir werden später darüber sprechen). In der Zwischenzeit werden wir uns die in osg :: Node definierten Methoden ansehen, mit denen übergeordnete Knoten bearbeitet werden:

1. getParent () - gibt einen Zeiger vom Typ osg :: Group zurück, der eine Liste der übergeordneten Knoten enthält.
   
2. getNumParants () - Gibt die Anzahl der übergeordneten Knoten zurück.
   
3. getParentalNodePath () - Gibt alle möglichen Pfade vom aktuellen Knoten zum Wurzelknoten der Szene zurück. Es gibt eine Liste von Variablen vom Typ osg :: NodePath zurück.
   

osg :: NodePath ist ein std :: -Vektor von Zeigern auf Szenenknoten.



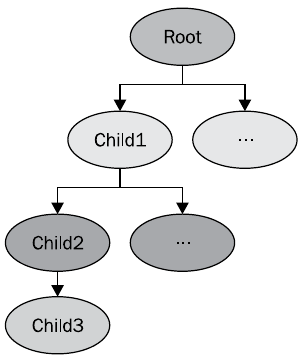
Beispiel für die in der Abbildung gezeigte Szene den folgenden Code

 osg::NodePath &nodePath = child3->getParentalNodePaths()[0]; for (unsigned int i = 0; i < nodePath.size(); ++i) { osg::Node *node = nodePath[i]; // -    } 

gibt die Knoten Root, Child1, Child2 zurück.

Sie sollten keine Speicherverwaltungsmechanismen verwenden, um auf übergeordnete Knoten zu verweisen. Wenn ein übergeordneter Knoten gelöscht wird, werden alle untergeordneten Knoten automatisch gelöscht, was zu einem Anwendungsabsturz führen kann.

3. Hinzufügen mehrerer Modelle zum Szenenbaum

Wir veranschaulichen den Mechanismus zur Verwendung von Gruppen anhand des folgenden Beispiels.


Grundsätzlich unterscheidet sich das Beispiel von allen vorherigen darin, dass wir zwei dreidimensionale Modelle laden. Um sie der Szene hinzuzufügen, erstellen wir einen Gruppenstammknoten und fügen unsere Modelle als untergeordnete Knoten hinzu

 osg::ref_ptr<osg::Group> root = new osg::Group; root->addChild(model1.get()); root->addChild(model2.get()); 

Als Ergebnis erhalten wir eine Szene, die aus zwei Modellen besteht - einem Flugzeug und einer lustigen Spiegelkuh. Eine Spiegelkuh ist übrigens kein Spiegel, es sei denn, Sie kopieren ihre Textur aus OpenSceneGraph-Data / Images / Reflect.rgb in das Verzeichnis data / Images unseres Projekts.

Die osg :: Group-Klasse kann alle Knotentypen als untergeordnete Knoten akzeptieren, einschließlich Knoten ihres Typs. Im Gegenteil, die Klasse osg :: Geode enthält überhaupt keine untergeordneten Knoten - es handelt sich um einen Endknoten, der die Geometrie des Szenenobjekts enthält. Diese Tatsache ist praktisch, wenn Sie fragen, ob der Knoten ein Knoten vom Typ osg :: Group oder ein anderer Ableitungstyp von osg :: Node ist. Schauen wir uns ein kleines Beispiel an.

 osg::ref_ptr<osg::Group> model = dynamic_cast<osg::Group *>(osgDB::readNodeFile("../data/cessna.osg")); 

Der von der Funktion osgDB :: readNodeFile () zurückgegebene Wert ist immer vom Typ osg :: Node *, kann jedoch in seinen Nachkommen osg :: Group * konvertiert werden. Wenn der Cessna-Modellknoten ein Gruppenknoten ist, ist die Konvertierung erfolgreich, andernfalls gibt die Konvertierung NULL zurück.

Sie können auch den gleichen Trick ausführen, der bei den meisten Compilern funktioniert

 //      osg::ref_ptr<osg::Group> group = ...; //     osg::Node* node1 = dynamic_cast<osg::Node*>( group.get() ); //      osg::Node* node2 = group.get(); 

An leistungskritischen Code-Stellen ist es besser, spezielle Konvertierungsmethoden zu verwenden

 osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("cessna.osg"); osg::Group* convModel1 = model->asGroup(); //   osg::Geode* convModel2 = model->asGeode(); //  NULL. 

4. Knoten der Transformation

Osg :: Group-Knoten können keine Transformationen vornehmen, außer die Möglichkeit, zu ihren untergeordneten Knoten zu wechseln. OSG bietet die Klasse osg :: Transform für die Bewegung der räumlichen Geometrie. Diese Klasse ist ein Nachfolger der osg :: Group-Klasse, aber auch abstrakt - in der Praxis werden stattdessen ihre Erben verwendet, die verschiedene räumliche Transformationen der Geometrie implementieren. Beim Durchlaufen des Szenendiagramms fügt der Knoten osg :: Transform seine Transformation der aktuellen OpenGL-Transformationsmatrix hinzu. Dies entspricht dem Multiplizieren der OpenGL-Transformationsmatrizen mit dem Befehl glMultMatrix ()



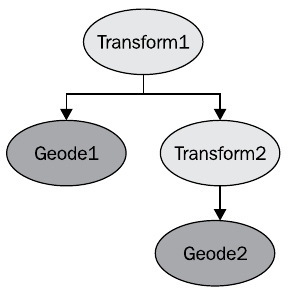
Dieses Beispielszenendiagramm kann in den folgenden OpenGL-Code übersetzt werden

 glPushMatrix(); glMultMatrix( matrixOfTransform1 ); renderGeode1(); glPushMatrix(); glMultMatrix( matrixOfTransform2 ); renderGeode2(); glPopMatrix(); glPopMatrix(); 

Wir können sagen, dass die Position von Geode1 im Koordinatensystem Transform1 und die Position von Geode2 im Koordinatensystem Transform2 festgelegt ist, versetzt zu Transform1. Gleichzeitig kann die Positionierung in absoluten Koordinaten in OSG aktiviert werden, was zum Verhalten des Objekts führt, das dem Ergebnis des OpenGL-Befehls glGlobalMatrix () entspricht

 transformNode->setReferenceFrame( osg::Transform::ABSOLUTE_RF ); 

Sie können in den relativen Positionierungsmodus zurückkehren

 transformNode->setReferenceFrame( osg::Transform::RELATIVE_RF ); 

5. Das Konzept einer Koordinatentransformationsmatrix

Der Typ osg :: Matrix ist ein grundlegender OSG-Typ, der nicht von intelligenten Zeigern gesteuert wird. Es bietet eine Schnittstelle zu Operationen auf 4x4-Matrizen, die die Transformation von Koordinaten beschreiben, z. B. Verschieben, Drehen, Skalieren und Berechnen von Projektionen. Die Matrix kann explizit angegeben werden.

 //   44 osg::Matrix mat(1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f ); 

Die osg :: Matrix-Klasse bietet die folgenden öffentlichen Methoden:

1. postMult () und operator * () - die richtige Multiplikation der aktuellen Matrix mit der als Parameter übergebenen Matrix oder dem Vektor. Die preMult () -Methode führt eine Linksmultiplikation durch.
   
2. makeTranslate (), makeRotate () und makeScale () - setzen die aktuelle Matrix zurück und erstellen eine 4x4-Matrix, die die Bewegung, Drehung und Skalierung beschreibt. Mit ihren statischen Versionen translate (), rotate () und scale () kann ein Matrixobjekt mit bestimmten Parametern erstellt werden.
   
3. invert () - berechnet die Inverse der aktuellen Matrix. Die statische Version von inverse () verwendet eine Matrix als Parameter und gibt eine neue Matrix zurück, die invers zu der angegebenen Matrix ist.
   

OSG versteht Matrizen als Matrizen von Strings und Vektoren als Strings. Um eine Matrixtransformation auf einen Vektor anzuwenden, tun Sie dies

 osg::Matrix mat = …; osg::Vec3 vec = …; osg::Vec3 resultVec = vec * mat; 

Die Reihenfolge der Matrixoperationen ist leicht zu verstehen, wenn man sich ansieht, wie Matrizen multipliziert werden, um eine äquivalente Umwandlung zu erhalten

 osg::Matrix mat1 = osg::Matrix::scale(sx, sy, sz); osg::Matrix mat2 = osg::Matrix::translate(x, y, z); osg::Matrix resultMat = mat1 * mat2; 

Der Entwickler muss den Transformationsprozess von links nach rechts lesen. Das heißt, in dem beschriebenen Codefragment skaliert der Vektor zuerst und dann seine Bewegung.

osg :: Matrixf enthält Elemente vom Typ float.

6. Verwenden der osg :: MatrixTransform-Klasse

Wir wenden das in der Praxis gewonnene theoretische Wissen an, indem wir zwei Flugzeugmodelle an verschiedenen Stellen in der Szene laden.


Das Beispiel ist eigentlich ziemlich trivial. Laden des Flugzeugmodells aus der Datei

 osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg"); 

Erstellen Sie einen Transformationsknoten

 osg::ref_ptr<osg::MatrixTransform> transform1 = new osg::MatrixTransform; 

Wir stellen das Modell so ein, dass das Modell entlang der X-Achse 25 Einheiten nach links als Transformationsmatrix verschoben wird

 transform1->setMatrix(osg::Matrix::translate(-25.0, 0.0, 0.0)); 

Wir legen unser Modell für den Transformationsknoten als untergeordneten Knoten fest

 transform1->addChild(model.get()); 

Wir machen dasselbe mit der zweiten Transformation, aber als Matrix setzen wir die Bewegung um 25 Einheiten nach rechts

 osg::ref_ptr<osg::MatrixTransform> transform2 = new osg::MatrixTransform; transform2->setMatrix(osg::Matrix::translate(25.0, 0.0, 0.0)); transform2->addChild(model.get()); 

Wir erstellen einen Wurzelknoten und setzen als Transformationsknoten dafür die Transformationsknoten transform1 und transform2

 osg::ref_ptr<osg::Group> root = new osg::Group; root->addChild(transform1.get()); root->addChild(transform2.get()); 

Erstellen Sie einen Viewer und übergeben Sie den Stammknoten als Szenendaten

 osgViewer::Viewer viewer; viewer.setSceneData(root.get()); 

Das Ausführen des Programms ergibt ein solches Bild



Die Struktur des Szenendiagramms in diesem Beispiel ist wie folgt.



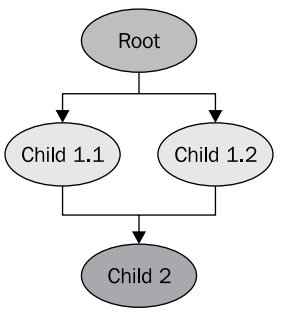
Wir sollten nicht durch die Tatsache verwirrt werden, dass sich die Transformationsknoten (Child 1.1 und Child 1.2) auf dasselbe untergeordnete Objekt des Flugzeugmodells (Child 2) beziehen. Dies ist ein regulärer OSG-Mechanismus, wenn ein untergeordneter Knoten eines Szenendiagramms mehrere übergeordnete Knoten haben kann. Daher müssen wir nicht zwei Instanzen des Modells in unserem Speicher speichern, um zwei identische Ebenen in der Szene zu erhalten. Mit diesem Mechanismus können Sie sehr effizient Speicher in der Anwendung zuweisen. Das Modell wird erst aus dem Speicher gelöscht, wenn es als untergeordnetes Element, mindestens ein Knoten, bezeichnet wird.

In ihrer Aktion entspricht die Klasse osg :: MatrixTransform den OpenGL-Befehlen glMultMatrix () und glLoadMatrix (), implementiert alle Arten von räumlichen Transformationen, ist jedoch schwierig zu verwenden, da die Transformationsmatrix berechnet werden muss.

Die Klasse osg :: PositionAttitudeTransform funktioniert wie die OpenGL-Funktionen glTranslate (), glScale (), glRotate (). Es bietet öffentliche Methoden zum Konvertieren von untergeordneten Knoten:

1. setPosition () - Verschiebt den Knoten an einen bestimmten Punkt im Raum, der durch den Parameter osg :: Vec3 angegeben wird
   
2. setScale () - skaliert das Objekt entlang der Koordinatenachsen. Skalierungsfaktoren entlang der entsprechenden Achsen werden durch einen Parameter vom Typ osg :: Vec3 festgelegt
   
3. setAttitude () - Legt die räumliche Ausrichtung des Objekts fest. Als Parameter wird die Rotationskonvertierungsquaternion osg :: Quat verwendet, deren Konstruktor mehrere Überladungen aufweist, mit denen Sie die Quaternion sowohl direkt (komponentenweise) als auch beispielsweise über die Euler-Winkel osg :: Quat (xAngle, osg :: X_AXIS, yAngle, osg) angeben können :: Y_AXIS, zAngle, osg :: Z_AXIS) (Winkel werden im Bogenmaß angegeben!)
   

7. Knoten wechseln

Stellen Sie sich eine andere Klasse vor - osg :: Switch, mit der Sie das Rendern eines Szenenknotens abhängig von einer logischen Bedingung anzeigen oder überspringen können. Es ist ein Nachkomme der osg :: Group-Klasse und fügt jedem ihrer untergeordneten Elemente einen logischen Wert hinzu. Es gibt mehrere nützliche öffentliche Methoden:

1. Überladenes addChild () verwendet als zweiten Parameter einen logischen Schlüssel, der angibt, ob dieser Knoten angezeigt werden soll oder nicht.
   
2. setValue () - legt den Sichtbarkeits- / Unsichtbarkeitsschlüssel fest. Es nimmt den Index des für uns interessanten untergeordneten Knotens und den gewünschten Schlüsselwert. Dementsprechend können Sie mit getValue () den aktuellen Schlüsselwert anhand des Index des für uns interessanten Knotens abrufen.
   
3. setNewChildDefaultValue () - Legt den Standardwert für den Sichtbarkeitsschlüssel aller neuen Objekte fest, die als untergeordnete Objekte hinzugefügt wurden.
   

Betrachten Sie die Anwendung dieser Klasse anhand eines Beispiels.


Das Beispiel ist trivial - wir laden zwei Modelle: eine konventionelle Cessna und eine Cessna mit der Wirkung eines brennenden Motors

 osg::ref_ptr<osg::Node> model1 = osgDB::readNodeFile("../data/cessna.osg"); osg::ref_ptr<osg::Node> model2 = osgDB::readNodeFile("../data/cessnafire.osg"); 

Wir erstellen jedoch osg :: Switch als Stammknoten, sodass wir beim Hinzufügen von Modellen als untergeordnete Knoten den Sichtbarkeitsschlüssel für jeden von ihnen festlegen können

 osg::ref_ptr<osg::Switch> root = new osg::Switch; root->addChild(model1.get(), false); root->addChild(model2.get(), true); 

Das heißt, Modell1 wird nicht gerendert, und Modell2 wird gerendert, was wir durch Ausführen des Programms beobachten werden



Durch Vertauschen der Tastenwerte sehen wir das entgegengesetzte Bild

 root->addChild(model1.get(), true); root->addChild(model2.get(), false); 

Wenn wir beide Tasten spannen, sehen wir zwei Modelle gleichzeitig

 root->addChild(model1.get(), true); root->addChild(model2.get(), true); 

Mit der setValue () -Methode können Sie die Sichtbarkeit und Unsichtbarkeit eines Knotens, eines untergeordneten Elements von osg :: Switch, direkt unterwegs aktivieren

 switchNode->setValue(0, false); switchNode->setValue(0, true); switchNode->setValue(1, true); switchNode->setValue(1, false); 

Fazit

In diesem Tutorial haben wir uns alle wichtigen Zwischenknotenklassen angesehen, die in OpenSceeneGraph verwendet werden. Damit haben wir einen weiteren Grundstein für das Wissen über das Gerät dieser zweifellos interessanten Grafik-Engine gelegt. Die im Artikel beschriebenen Beispiele sind nach wie vor in meinem Repository auf Github verfügbar .

Fortsetzung folgt...