Es gibt eine Reihe von Aufgaben, bei denen ein Langzeitsignal in Segmente unterteilt wird, von denen jedes separat verarbeitet wird. Insbesondere wird dieser Ansatz verwendet, um das Signal unter Verwendung der Fenster-Fourier-Transformation oder umgekehrt bei der Synthese zu analysieren; sowie bei der spektralen Verarbeitung wie Rauschunterdrückung, Tempowechsel, nichtlineare Filterung, Audiodatenkomprimierung und anderen.

Der Prozess der Partitionierung selbst wird mathematisch durch Multiplikation mit einer Gewichtsfunktion ( Fensterfunktion ) mit einem Versatz dargestellt. Für das einfachste Fenster - rechteckig - könnte es so aussehen:

Quellensignal:



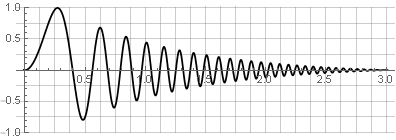
Partitionen:







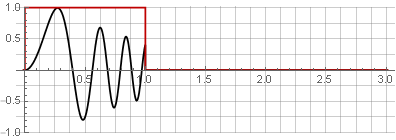
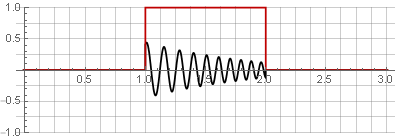
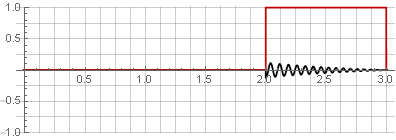
Sie können das ursprüngliche Signal wiederherstellen, indem Sie es einfach addieren.

Weitere Details

Jedoch von Aus einer Reihe von Gründen ist eine Rechteckfunktion nicht die beste Fensterfunktion. Bei der Spektralanalyse scheint der analysierte Datenblock durch die (normalerweise schnelle) diskrete Fourier-Transformation eine „Schleife“ zu bilden, was zu einer Lücke an den Rändern und einer Verzerrung des Spektrums führt:



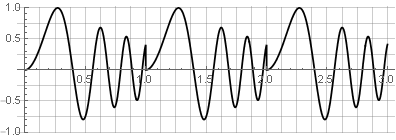
Es ist auch nicht für die umgekehrte Synthese geeignet - da jede Änderung auch zu Brüchen führt - zum Beispiel, wenn wir versuchen, einen der Teile umzukehren:



Um diese Nachteile zu beseitigen, wird eine Überlappung verwendet, wenn jedes nachfolgende Fenster einen Teil der Daten aus dem vorherigen erfasst. bzw. das Gewichtsfenster fällt allmählich auf die Kanten.

Überlappung bei 50%

Am häufigsten verwenden sie das Hannah-Fenster (auch als „Raised Cosine“ bezeichnet) mit einer Überlappung von 50%:








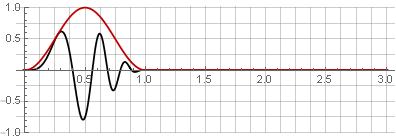
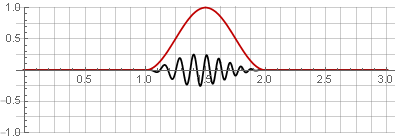
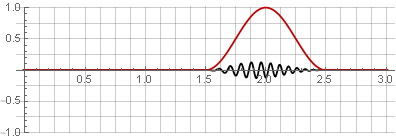
Aufgrund der Symmetrie der Kosinusfunktion während der Addition werden sie zu Eins summiert:



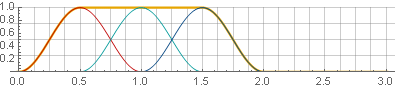
Mit der umgekehrten Synthese erhalten wir keine Lücken - sondern nur unter der Bedingung, dass die Werte an den Fensterrändern immer noch auf Null gehen. Wenn Sie beispielsweise eines der Teile umkehren, wird die Glätte nicht verletzt:

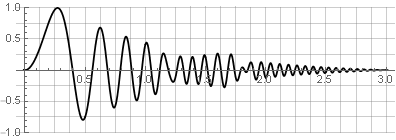
Doppelte Überlagerungsverarbeitung

Betrachten Sie den Algorithmus zum Verarbeiten eines Signals unter Verwendung einer schnellen Fourier-Transformation (FFT) genauer:

1. Aufteilen des Signals in Segmente mit einer Fensterüberlagerung;
2. direkte FFT;
3. Spektrumverarbeitung;
4. inverse FFT;
5. wiederholte Fensterüberlagerung (da nach der umgekehrten FFT die Ränder nicht unbedingt auf Null andocken, ohne zu brechen);
6. Summation der resultierenden Segmente.

Wenn keine Spektrumverarbeitung durchgeführt wird, sollte das Ausgangssignal mit dem Eingangssignal identisch sein (nur mit einer unvermeidlichen Zeitverzögerung).

Bei Verwendung des Hann-Fensters reicht eine Überlappung von 50% nicht mehr aus, da Einbrüche auftreten:



Da doppelte Überlappung gleichbedeutend mit Quadrieren ist, besteht die offensichtliche Lösung darin, die Wurzel des Hann-Fensters zu verwenden, um das Quadrieren zu kompensieren:



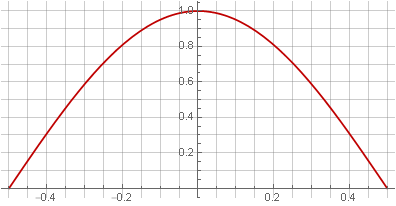
In diesem Fall war das Fenster an den Rändern jedoch nicht mehr glatt - in der ersten Ableitung trat eine Lücke auf.


Sie können auch in die andere Richtung gehen - verwenden Sie die Überlappung von 75%, und dann werden die Fenster auch zu einer Konstanten summiert - nur nicht in $$$1$ und in $$$\ frac {3} {2}$ ::



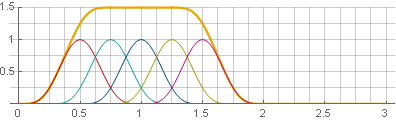
In diesem Fall hatten wir einfach Glück. Wenn wir das Quadrat in die Summe erweitern, können wir sehen, dass es sich um eine Komposition aus zwei Hannah-Fenstern handelt, jedoch in unterschiedlichen Maßstäben, wodurch wir die Anforderungen erfüllen können, die wir benötigen:

$$

$$\ left (\ frac {\ cos (2 \ pi x) +1} {2} \ right) ^ 2 = \ frac {\ cos (2 \ pi x) +1} {2} + \ frac {\ cos (4 \ pi x) -1} {8}$$

Bei anderen Fensterfunktionen funktioniert ein solcher Trick nicht. Außerdem können nicht alle Standardfensterfunktionen selbst bei einer Überlappung von 50% eine Summierung in einer Konstanten liefern.

Idee

Wir können das Hann-Fenster nicht als unabhängige Funktion betrachten, sondern als den Unterschied zwischen zwei stückweise stetigen Funktionen (ein separater Artikel wurde einer ausführlichen Diskussion gewidmet) mit einem Versatz. Verwenden Sie beispielsweise die folgende Funktion

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ \ sin \ left (\ frac {\ pi x} {2} \ right) & -1 <x <1 \\ \ end {array} \ right.$$

kann schreiben

$$

$$f (x + 1) -f (x-1)$$

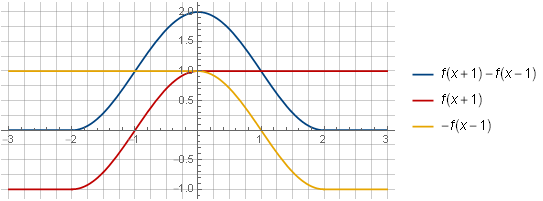
Wenn man die Komponenten der Summe zweier solcher Fenster betrachtet, wird ihre Fähigkeit, sie zu einer Konstanten zusammenzufassen, visueller:



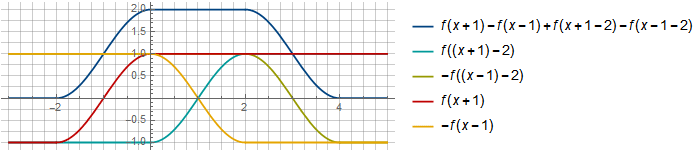
Auf dem Segment $$$[0,2]$ Wir haben zusätzlich zu den Funktionen eine gegenseitige Entschädigung erhalten $$$-f (x-1)$ und $$$f ((x + 1) -2)$ seit $$$f ((x + 1) -2) = f (x-1)$

Sie können einen anderen Versatz mit mehr Überlappung auswählen, zum Beispiel:

$$

$$f \ left (x + \ frac {1} {2} \ right) -f \ left (x- \ frac {1} {2} \ right)$$

Und dann beim schrittweisen Schalten $$$\ frac {1} {2}$ werden sie auch zu einer Konstanten summiert:



Es ist ersichtlich, dass Sie die gleichen Hann-Fenster erhalten, wenn Sie die Komponenten der Fensterfunktion neu anordnen.

Somit ist es unter Verwendung verschiedener Beschränkungsfunktionen möglich, Fenster mit der erforderlichen Form zu bilden.

Endgültige Formel

Jetzt muss nur noch die Skalierung so eingestellt werden, dass die Definitionsbereiche und Werte nicht vom Ausmaß der Überlappung abhängen. Fenster in einem Intervall definieren $$$[0,1]$ wir bekommen

$$

$$\ frac {f \ left (\ frac {2 tx} {t-1} -1 \ right) -f \ left (\ frac {2 t (x-1)} {t-1} +1 \ right) } {2}$$

wo $$$f$ - stückweise stetige Funktion der Form

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ g (x) & -1 <x <1 \\ \ end {array} \ richtig.$$

aber $$$g$ - eine Interpolationsfunktion zwischen Punkten $$$(- 1, -1)$ und $$$(1,1)$ .

Parameter $$$t$ bestimmt den Grad der Überlappung - ein Teiler, der den Schritt bestimmt, um den jedes nächste Fenster verschoben werden muss, $$$x_ {n + 1} = x_n + \ frac {1} {t}$ und muss größer als eins sein, $$$t> 1$ .

Überlappungsprozentsatz $$$p$ kann durch die Formel berechnet werden

$$

$$p = \ frac {100 (t-1)} {t}$$

und umgekehrt

$$

$$t = \ frac {100} {100-p}$$

Das endgültige Erscheinungsbild des Fensters hängt sowohl von der Wahl des Überlappungsgrades als auch von der Wahl der Begrenzungsfunktion ab.

Einige interessante Beispiele

Hier sehen wir uns einige vorgefertigte Lösungen an, für die alles gestartet wurde. Der Einfachheit halber betrachten wir eine einfach interpolierende Funktion $$$g (x)$ ohne andere Umreifung.

Polynomfenster

Sie sind am wenigsten rechenintensiv. Verwendung der zuvor abgeleiteten Formel

$$

$$\ frac {2 x \ Gamma \ left (n + \ frac {1} {2} \ right) \, _2F_1 \ left (\ frac {1} {2}, 1-n; \ frac {3} {2} ; x ^ 2 \ right)} {\ sqrt {\ pi} \ Gamma (n)}$$

Wir erhalten ein Polynom mit einer gegebenen Anzahl von Nullen auf höheren Ableitungen, die die notwendige Glätte des Fensters an den Rändern liefern.


Bei einer 75% igen Überlappung des Fensters mit unterschiedlichen Werten von n sehen die Fenster folgendermaßen aus:



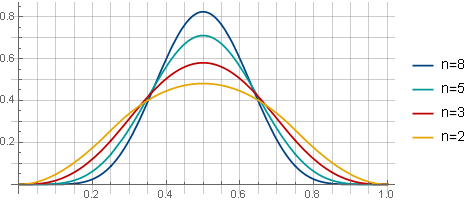
Und im Fall der Wurzelextraktion - so (bei Verwendung von 75% Überlappung):



oder so (bei Verwendung von 50% Überlappung):

Das glatteste Fenster

Funktion

$$

$$\ tanh \ left (\ frac {k x} {\ sqrt {1-x ^ 2}} \ right)$$

Es ist insofern interessant, als es unendlich differenzierbar ist und alle seine Ableitungen an den Rändern 0 sind (was durch Berücksichtigung seiner Ableitungen auf der Grundlage von Differenzierungsregeln bewiesen werden kann - in jedem Term gibt es einen Nullungsfaktor). Dies ermöglicht es uns, Fenster auf seiner Basis zu erstellen, deren Ableitungen keine Lücken aufweisen:

Fensteransicht "Rock"

Die Notwendigkeit für diesen Fenstertyp wird durch Erhöhen der FFT-Auflösung verursacht, aber durch Verringern ihrer Konzentration im Zentrum wird der Effekt des Effekts "Zeit-Frequenz-Unsicherheit" bei hohen Frequenzen verringert.

Zunächst bestimmen wir den gewünschten Typ der Fensterfunktion - zum Beispiel wie folgt:

$$

$$- \ log \ left (k ^ 2 x ^ 2 + 1 \ right) + \ log \ left (k ^ 2 + 1 \ right) - \ frac {k ^ 2 \ left (1-x ^ 2 \ right) } {k ^ 2 + 1}$$

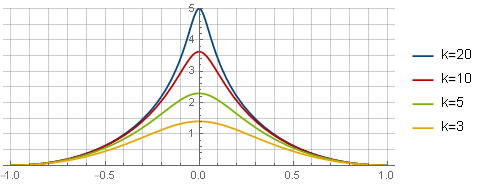
Hier bestimmt der erste Term die Form der Funktion selbst, der zweite - liefert den Schnittpunkt mit der Abszissenachse, der dritte (Parabel) setzt die Ableitung an den Rändern für ein reibungsloses Andocken zurück; und der Parameter $$$k$ definiert die "Schärfe" des Peaks. In dieser Form ist es noch nicht für die Verwendung geeignet - zuerst müssen Sie die Einschränkungsfunktion durch Integration und Skalierung daraus erhalten:

$$

$$\ frac {kx \ left (k ^ 2 \ left (x ^ 2 + 3 \ right) +6 \ right) +3 \ left (k ^ 2 + 1 \ right) \ left (kx \ left (\ log \) links (k ^ 2 + 1 \ rechts) - \ log \ links (k ^ 2 x ^ 2 + 1 \ rechts) \ rechts) -2 \ tan ^ {- 1} (kx) \ rechts)} {4 k ^ 3-6 \ left (k ^ 2 + 1 \ right) \ tan ^ {- 1} (k) +6 k}$$

Der Einfachheit halber können Sie den Parameter binden $$$k$ auf das Niveau der Überlappung $$$t$ - zum Beispiel, so dass die 4. Ableitung in der Mitte des Fensters 0 ist - und dann $$$k$ wird als betrachtet $$$\ sqrt {3} (t-1)$ ::



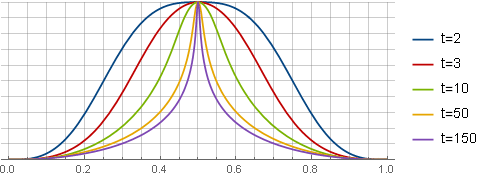
Hier sind aus Gründen der Übersichtlichkeit alle Fenster auf den gleichen Maßstab verkleinert.

Nadelansichtsfenster

Es ist eine "aggressivere" Version des vorherigen Fensters. Als Grundlage wurde eine Übertreibung gewählt, von der aus durch sukzessive Transformationen

$$

$$\ frac {1} {x} \ bis \ frac {1} {\ sqrt {x ^ 2}} \ bis \ frac {1} {\ sqrt {x ^ 2 + 1}} \ bis \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \ to \ frac {\ left (1-x ^ 2 \ right) ^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

und mit den gleichen Schritten in Form von Integration und Skalierung bekam die Formel

$$

$$\ frac {kx \ left (2 k ^ 2 \ left (x ^ 2-4 \ right) -3 \ right) \ sqrt {k ^ 2 x ^ 2 + 1} + \ left (8 \ left (k ^) 4 + k ^ 2 \ rechts) +3 \ rechts) \ sinh ^ {- 1} (kx)} {\ links (8 \ links (k ^ 4 + k ^ 2 \ rechts) +3 \ rechts) \ sinh ^ {-1} (k) -3 k \ sqrt {k ^ 2 + 1} \ left (2 k ^ 2 + 1 \ right)}$$

Hier können Sie auch den Parameter binden $$$k$ auf das Niveau der Überlappung. Die direkte Lösung der Gleichung der 4. Ableitung ergibt ein umständliches Ergebnis. Erstellen Sie also einfach das Bild für das vorherige Fenster im Bild und die Ähnlichkeit durch Definieren $$$k$ wie $$$k (t-1)$ Dadurch wird die Rolle des Parameters sichergestellt $$$k$ als "Feinabstimmung". Bei $$$k = 2,22$ Fenster sehen folgendermaßen aus:

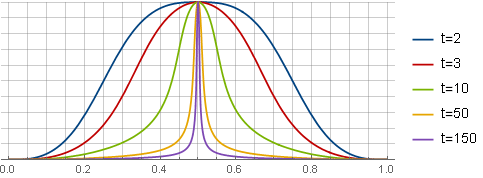
Asymmetrisches Fenster

Die Fensterfunktion muss überhaupt nicht symmetrisch sein. Nehmen wir an, wir brauchen ein Fenster mit einem scharfen Angriff und einer gleichmäßigen Dämpfung. Wir können es nach einem bereits bekannten Schema erhalten - zuerst die gewünschte Form der Funktion bestimmen und dann durch Integration die Restriktionsfunktion erhalten. Hier ist die Aufgabe etwas komplizierter, da das Zentrum aufgrund von Asymmetrie den Ursprung nicht mehr durchläuft, sodass ein zusätzlicher Berechnungsschritt hinzugefügt wird. Dies führt auch dazu, dass die Formeln dadurch eher umständlich sind. Betrachten Sie zum Beispiel die einfachste Option - eine Parabel multipliziert mit einem Polynomgewichtsfenster:

$$

$$(1-x) ^ 2 \ left (1-x ^ {10} \ right) ^ 2$$

Hier bestimmt der Grad von x im gewichteten Fenster (nämlich 10) die „Schärfe“ des Angriffs. Wir haben einen bestimmten Wert anstelle eines symbolischen Parameters verwendet, um die Formeln der Übersichtlichkeit halber zu vereinfachen. Wenn Sie möchten, können Sie ihn später neu berechnen.

Nach der Integration reicht eine einfache Skalierung nicht mehr aus - Sie müssen die Kanten noch ausrichten:



Dazu verschieben wir zuerst die Funktion nach oben, um den linken Rand auszurichten, skalieren sie dann auf die beiden am rechten Rand und subtrahieren einen. Dann erhalten wir die folgende Formel:

$$

$$\ frac {8775 \ left (\ frac {x ^ {27}} {27} - \ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25} - \ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14} - \ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \ right)} {9856} -1$$

Damit das endgültige Fenster das gewünschte Aussehen hat, muss auch ein ausreichend großer Überlappungsgrad bereitgestellt werden:

Fazit

Ebenso können Sie Fenster aus anderen glockenförmigen Funktionen erstellen - zum Beispiel Gaußschen; Sie können auch die bereits berücksichtigten ändern, um eine größere Glätte zu erzielen, oder die Form der Kurve ändern.

Aus Rücksicht blieb die spektrale Zusammensetzung solcher Fensterfunktionen erhalten - dies sollte gesondert untersucht werden.

Eine etwas fortgeschrittenere Version des Artikels (mit der Möglichkeit, die Parameter in den betrachteten Fenstern und versteckten Formeln dynamisch zu ändern) in Form eines Wolfram Mathematica-Dokuments kann hier heruntergeladen werden .