Wie viele Programmierer benötigen Sie, um zuvor geschriebenen Code zu unterstützen?

Vor einiger Zeit fand ein Gespräch zwischen mir und meinem guten Freund statt, in dem die folgenden Sätze erklangen:

- Die Anzahl der Programmierer wird ständig zunehmen - weil die Menge an Code wächst und immer mehr Entwickler ständig benötigt werden, um ihn zu unterstützen.
- Aber der Code altert, ein Teil davon verlässt die Unterstützung. Das Vorhandensein eines Gleichgewichts ist nicht ausgeschlossen.

Als ich sie einige Tage später zurückrief, fragte ich mich, ob die Codeunterstützung, die im Laufe der Zeit immer mehr Ressourcen erfordert, letztendlich die Entwicklung neuer Funktionen lähmen oder eine unbegrenzte Erhöhung der Anzahl der Programmierer erfordern würde. Mathematische Analysen und Differentialgleichungen halfen dabei, die Abhängigkeit des Unterstützungsvolumens von der Entwicklung qualitativ zu bewerten und Antworten auf Fragen zu finden.

Die erste Frage. Kann die Unterstützung alle Entwicklungsressourcen „essen“?

Stellen Sie sich ein Team von Programmierern vor, bei dem die Anzahl der Teilnehmer konstant ist. Anteil ihrer Arbeitszeit $$$\ mu (t)$( $$$0 <\ mu (t) <1$) entfielen auf die Entwicklung neuen Codes und den verbleibenden Teil der Zeit $$$1- \ mu (t)$geht zur Unterstützung. Nehmen wir unter den Annahmen des Modells an, dass die erste Art von Aktivität darauf abzielt, die Codemenge zu erhöhen, und die zweite darauf, sie zu ändern (Fehler zu korrigieren) und die Codemenge nicht wesentlich beeinflusst.

Wir bezeichnen $$$y (t)$Der gesamte Code wurde nach Zeit geschrieben $$$t$. Die Geschwindigkeit beim Schreiben von Code ist proportional $$$\ mu (t)$wir bekommen:

$$

$$\ frac {dy (t)} {dt} = a_0 \ mu (t); a_0 \ in \ mathbb {R}, a_0> 0.$$

Es ist natürlich anzunehmen, dass der Arbeitsaufwand für die Pflege des Codes proportional zu seinem Volumen ist:

$$

$$1- \ mu (t) = a_1 y (t); a_1 \ in \ mathbb {R}, a_1> 0$$

oder

$$

$$\ mu (t) = 1-a_1y (t)$$

Woher?

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1y (t))).$$

Wir erhalten eine Differentialgleichung, die sich leicht integrieren lässt. Wenn zum anfänglichen Zeitpunkt die Codemenge Null ist, dann

$$

$$y (t) = \ frac {1} {a_1} (1-e ^ {- a_0a_1t}).$$

Bei $$$t \ to + \ infty$Funktion $$$y (t) \ to1 / a_1$und $$$\ mu (t) \ bis 0$. Dies bedeutet eine schrittweise Reduzierung der Entwicklung neuer Funktionen auf Null im Laufe der Zeit und den Übergang aller Ressourcen zur Unterstützung.

Wenn jedoch rechtzeitig $$$h> 0$Da der Code veraltet ist und nicht mehr unterstützt wird, muss jeweils nur noch Code unterstützt werden $$$t$gleich $$$y (t) - y (t-h).$Dann

$$

$$1- \ mu (t) = a_1 (y (t) - y (t-h)),$$

$$

$$\ mu (t) = 1-a_1 (y (t) - y (t-h)),$$

aber $$$y (t)$ist eine Lösung einer Differentialgleichung mit einem verzögerten Argument [1]:

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1 (y (t) - y (t-h))).$$

Die Lösung dieser Gleichung wird eindeutig durch Einstellen der Werte bestimmt $$$y (t)$"Vor dem Beginn der Zeit", mit $$$t \ in [-h, 0]$. Da in unserem Fall vor dem ersten Mal kein Code geschrieben wurde $$$y (t) = 0$bei $$$t \ in [-h, 0]$.

Schauen wir uns einige Beispiele an. Wir werden die Zeit in Jahren und die Codemenge in Tausenden von Zeilen messen. Dann für $$$a_0$Werte in der Größenordnung von zehn sind akzeptabel, wir nehmen 50 und 100. Das heißt, in einem Jahr wird das Entwicklungsteam fünfzig bzw. einhunderttausend Codezeilen schreiben. Für $$$a_1$akzeptable Werte können sein: $$$0,25 / a_0$, $$$0.5 / a_0$, $$$1 / a_0$. Dies bedeutet, dass das Entwicklungsteam die Menge an Code, die es für das Jahr geschrieben hat, mit einer viertel, halben oder vollen Arbeitslast beibehalten kann. Als durchschnittliche Lebensdauer des Codes legen wir die Werte 1, 2 und 4 Jahre fest. Wenn wir die Gleichung numerisch lösen, erhalten wir Beispiele für das Verhalten der Funktion $$$\ mu (t)$für einige Kombinationen von Parametern $$$h, a_0, a_1$.

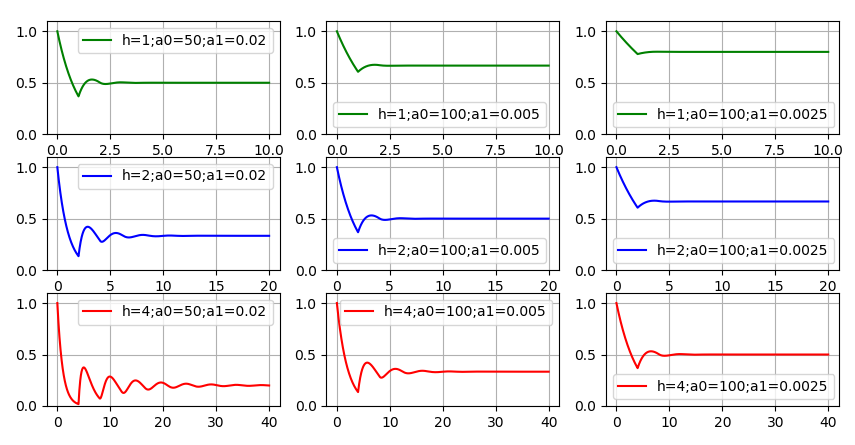
Funktionsverhalten $$$\ mu (t)$Angesichts des Alterns hat sich der Code geändert. Die Funktion ist nicht mehr eintönig, aber Schwankungen „beruhigen“ sich im Laufe der Zeit, es besteht eine Tendenz dazu $$$\ mu (t)$auf einen konstanten Wert. Diagramme zeigen: je mehr $$$h$, $$$a_0$und $$$a_1$Das heißt, je langsamer der Code älter wird, je schneller die Entwicklung von neuem Code erfolgt und je geringer die Qualität des Codes ist, desto weniger Ressourcen verbleiben für die Entwicklung neuer Funktionen. Es bestand der Wunsch, mindestens ein Beispiel dafür zu nennen $$$\ mu (t)$"Kuschelte" nahe Null. Dies erforderte jedoch die Auswahl sehr schlechter Indikatoren für die Entwicklungsqualität und eines Codes für die Langzeitalterung. Selbst in der unteren linken Grafik verbleibt eine erhebliche Menge an Ressourcen für die neue Funktionalität. Daher ist die richtige Antwort auf die erste Frage wahrscheinlicher: theoretisch - ja, es ist möglich; praktisch - kaum.

Fragen, die nicht beantwortet werden konnten:

1. Ist es wahr, dass $$$\ mu (t)$neigt zu einer gewissen Grenze für $$$t \ to + \ infty$für alle $$$a_0, a_1> 0$? Wenn nicht für alle, für welche?
2. Wenn die Grenze existiert, hängt es davon ab, wie ihr Wert ist $$$a_0, a_1$?

Die zweite Frage. Kann die Codeunterstützung die Anzahl der Programmierer unbegrenzt erhöhen?

Wir bezeichnen $$$q (t)$Anzahl der Programmierer, die an der Entwicklung neuen Codes beteiligt sind. Wie oben $$$y (t)$- die Menge an Code, die von der Zeit geschrieben wurde $$$t$. Dann

$$

$$\ frac {dy (t)} {dt} = a_2 q (t); a_2 \ in \ mathbb {R}, a_2> 0.$$

Lassen Sie die Code-Unterstützung beschäftigt $$$p (t)$Programmierer. Alterung des C-Codes

$$

$$p (t) = a_3 (y (t) -y (t-h)); a_3 \ in \ mathbb {R}, a_3> 0.$$

Woher?

$$

$$p (t) = a_3 \ int_ {t-h} ^ {t} \ frac {dy (s)} {ds} ds = a_2a_3 \ int_ {t-h} ^ tq (s) ds.$$

Wenn $$$q (t) \ leq C_1$dann

$$

$$p (t) \ leq a_1a_2C_1h.$$

Daher ist die Antwort auf die zweite Frage negativ: Wenn die Anzahl der Entwickler von neuem Code begrenzt ist, kann die Unterstützung im Zusammenhang mit dem Altern von Code nicht zu einer unbegrenzten Erhöhung der Anzahl von Programmierern führen.

Fazit

Die betrachteten Modelle sind „weiche“ mathematische Modelle [2]. Sie sind sehr einfach. Die Abhängigkeit der Simulationsergebnisse von den Parameterwerten entspricht jedoch der für reale Systeme erwarteten, was für die Angemessenheit der Modelle und eine ausreichende Genauigkeit spricht, um qualitative Schätzungen zu erhalten.

Referenzliste

1. Elsgolts L.E., Norkin S.B. Einführung in die Theorie der Differentialgleichungen mit abweichendem Argument. Moskau Verlag "Wissenschaft". 1971.
2. Arnold V.I. "Harte" und "weiche" mathematische Modelle. Moskau Verlag des Zentrums. 2004.