Welche Beweise können Mathematiker überzeugen, wenn es keine strengen Beweise gibt?

Das neue statistische Modell scheint die seit langem akzeptierten Annahmen der Zahlentheorie zu untergraben. Wie sehr können Sie ihr vertrauen, wenn nur strenge Beweise wirklich wichtig sind?

Welche Punkte auf der elliptischen Kurve y ² = x ³ - 4x + 1 sind rational? Um sie zu finden, müssen Sie Linien durch Paare rationaler Punkte ziehen. Alle Punkte, durch die die Linien verlaufen, sind ebenfalls rational.

Kürzlich haben vier Forscher ein Modell entwickelt, das den gesunden Menschenverstand ihres Forschungsgebiets auf den Kopf stellt. Sie verwendeten Berechnungsdaten, um darauf hinzuweisen, dass die über mehrere Jahrzehnte vorherrschende Ansicht eines der grundlegenden Konzepte falsch war.

Und das sind keine Biologen, Klimatologen oder Physiker. In ihrem wissenschaftlichen Bereich haben empirische Modelle kein Mitspracherecht in Bezug auf die Wahrheit. Sie sind Mathematiker, Vertreter der Disziplin, deren Standardwährung - ein unbestreitbarer logischer Beweis - sie normalerweise vor Debatten bewahrt, die andere Bereiche betreffen. Und doch sind sie hier, und ihr Modell sagt, dass es wahrscheinlich an der Zeit ist, einige der lang gehegten Ideen zu überarbeiten.

Ein Modell, das 2016 online veröffentlicht wurde und im Journal der Europäischen Mathematischen Gesellschaft erscheinen kann, gehört zu einem so ehrwürdigen mathematischen Konzept wie dem Rang einer algebraischen Gleichung. Der Rang ist ein Maß dafür, wie viele Lösungen der Gleichung sich auf rationale und welche auf irrationale Zahlen beziehen. Gleichungen von hohem Rang haben rationalere Lösungen und sind komplizierter.

Seit Beginn des 20. Jahrhunderts haben sich Mathematiker für die Frage interessiert, ob es Einschränkungen hinsichtlich der Höhe des Ranges der Gleichung gibt. Anfangs dachten fast alle, dass die Einschränkung bestehen sollte. In den 1970er Jahren hatte sich die vorherrschende Meinung geändert - die meisten Mathematiker begannen zu glauben, dass der Rang unbegrenzt sei, was bedeutet, dass es möglich ist, Kurven mit unendlich großen Rängen zu erkennen. So geschah es, obwohl einige Mathematiker glaubten, dass es keine starken Argumente für diese Meinung gab.

„Die Menschen sind sehr autoritär in Bezug auf das Fehlen von Einschränkungen. Wenn Sie jedoch anfangen zu verstehen, stellt sich heraus, dass die Beweise dafür äußerst schwach sind “, sagte Andrew Granville , Mathematiker an der Universität von Montreal und am University College London.

Heute deuten die Beweise auf etwas anderes hin. Zwei Jahre nach dem Erscheinen des Modells überzeugte sie viele Mathematiker davon, dass der Rang algebraischer Gleichungen eines bestimmten Typs wirklich begrenzt war. Allerdings glaubt nicht jeder, dass dieses Modell überzeugt. Mangelnde Übereinstimmung wirft Fragen auf, die nicht oft mit mathematischen Ergebnissen zusammenhängen. Welches Gewicht können empirische Beweise in einem Bereich haben, in dem nur strenge Beweise von Bedeutung sind?

"Es gibt keine mathematische Rechtfertigung dafür, dass dieses Modell genau das ist, was wir brauchen", sagte Jennifer Park , Mathematikerin an der Ohio University, Mitautorin der Arbeit. "Außerdem funktionieren aus experimenteller Sicht viele Dinge."

Punkt zu Punkt

Wenn Sie eine Gleichung erhalten, können Sie eine Kurve ihrer Lösungen in der Grafik zeichnen. Mathematiker möchten wissen, wie viele dieser Lösungen rational sind - sie gehören zur Art der Zahlen, die als Verhältnis zweier Ganzzahlen (1/2, -3 oder 4483/929) ausgedrückt werden können.

Rationale Lösungen sind systematisch schwer zu finden, aber Mathematiker verfügen über Techniken, die unter bestimmten Bedingungen funktionieren. Nehmen Sie die Gleichung x ² + y ² = 1. Der Graph der Lösungen für diese Gleichung ist ein Kreis. Um alle rationalen Punkte des Kreises zu finden, beginnen wir mit einer bestimmten Lösung - sagen wir, ab dem Punkt, an dem x = 1 und y = 0 ist. Zeichnen Sie dann eine Linie durch diesen Punkt, die den Kreis an einem anderen Punkt schneidet. Wenn die Steigung unserer Linie rational ist, ist der zweite Schnittpunkt ebenfalls eine rationale Lösung. Durch das Zeichnen einer Linie haben wir die Anzahl der rationalen Entscheidungen von eins auf zwei erhöht.



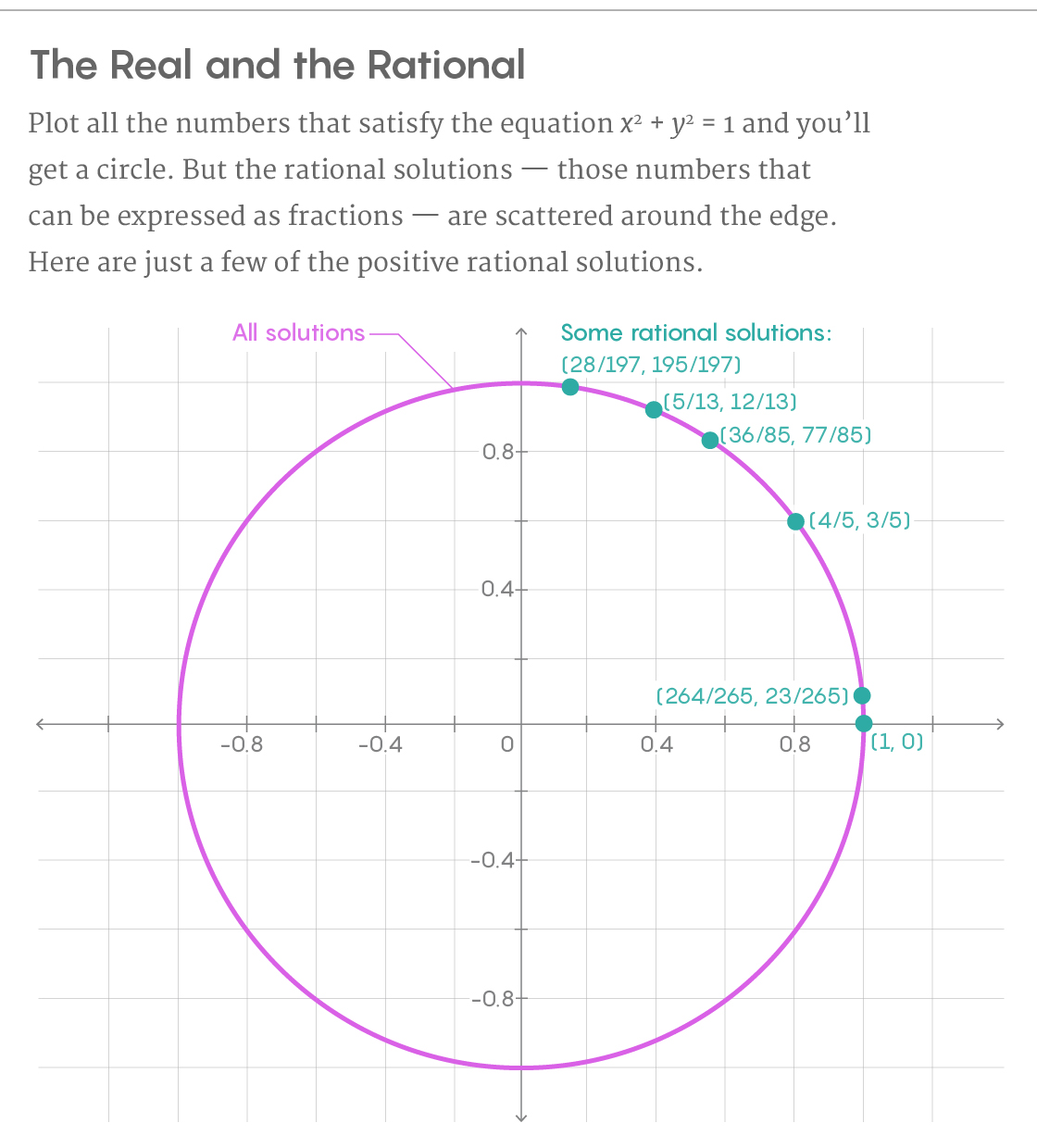
Und es besteht keine Notwendigkeit, hier anzuhalten. Wir wiederholen den Vorgang, indem wir eine gerade Linie mit einer anderen rationalen Steigung durch den zweiten rationalen Punkt ziehen - sie schneidet den Kreis am dritten rationalen Punkt. Wenn wir diesen Weg bis ins Unendliche fortsetzen, werden wir schließlich alle rationalen Punkte des Kreises finden, von denen es eine unendliche Zahl gibt.

Und im Fall eines Kreises müssen Sie nur an einem Punkt beginnen, und Sie können alle finden. Die Anzahl der rationalen Entscheidungen, die Sie zu Beginn kennen müssen, um alle anderen zu finden, wird als Rang der Kurve bezeichnet. Der Rang ist eine gute Möglichkeit, eine unendliche Menge rationaler Entscheidungen in einer einzigen Zahl zu beschreiben. "Es ist sozusagen die beste Art, die rationalen Lösungen für diese Kurven zu beschreiben", sagte Björn Puunen , Mathematiker am MIT, Co-Autor des Modells, zusammen mit Park, John Voight vom Dartmouth College und Melanie Matchet Wood von der University of Wisconsin.

Ein Kreis ist eine quadratische Gleichung oder eine Gleichung zweiten Grades („Grad“ bedeutet die Größe des größten Grades der Terme der Gleichung). Seit mehr als hundert Jahren wissen Mathematiker, wie man rationale Lösungen für Gleichungen zweiten Grades findet.

Die nächste Art von Gleichungen sind elliptische Kurven, in denen Variablen auf den dritten Grad angehoben werden. Elliptische Kurven existieren im attraktivsten Bereich der mathematischen Forschung. Sie sind komplizierter als Gleichungen zweiter Ordnung, daher sind sie interessant zu studieren, aber nicht zu kompliziert. Das geänderte Verfahren zum Zeichnen von geraden Linien gilt weiterhin für elliptische Kurven, funktioniert jedoch nicht mehr mit Gleichungen vierter Ordnung und höher.

Elliptische Kurven gibt es in verschiedenen Rängen. Bei einigen elliptischen Kurven können Sie von einem rationalen Punkt aus beginnen, das Verfahren zum Zeichnen von Linien anwenden und nicht alle rationalen Lösungen finden. Möglicherweise müssen Sie einen zweiten rationalen Punkt hinzufügen, der nicht mit dem ersten zusammenhängt. Damit beginnen Sie ein neues Verfahren zum Zeichnen von Linien und finden ein Gleichgewicht rationaler Punkte. Eine Kurve, um alle rationalen Punkte zu finden, von denen Sie zunächst zwei rationale Punkte kennen müssen, hat einen Rang von zwei.

Es gibt keine nachgewiesene Beschränkung der Höhe des Ranges einer elliptischen Kurve. Je höher der Rang der Gleichung ist, desto breiter und komplexer ist die Menge der rationalen Lösungen der Kurve. "Der Rang misst irgendwie die Komplexität der Entscheidungen", sagte Puunen.

Trotzdem entzieht sich der Rang den Versuchen der Mathematiker, ihn theoretisch zu beschreiben. Wenn Sie eine elliptische Kurve erhalten, besteht keine offensichtliche Beziehung zwischen dem Aussehen und dem Rang. "Wenn ich eine elliptische Kurve habe und die Koeffizienten ein wenig anpasse, ändert sich ihr Rang radikal", sagte Park. - Sie können den Koeffizienten um eins ändern, und der Rang springt in eine Million. Niemand weiß, wie sich die Reihen verhalten. “

Das Fehlen einer allgemeinen Theorie veranlasste die Mathematiker, sich auf die kleinen Beweise zurückzuziehen, die sie haben, um über die Existenz einer Rangbeschränkung zu spekulieren. "Der Standpunkt ist, dass es keine Einschränkungen für den Rang gibt, weil die Leute immer mehr hohe Ränge fanden", sagte Granville. Der aktuelle Rekordhalter ist eine elliptische Kurve mit Rang 28, die 2006 von Noam Elkis, einem Mathematiker an der Harvard University, entdeckt wurde.

Aber dann erschien dieses neue Modell und erklärte, dass es mit ziemlicher Sicherheit das Ende der Straße sei.

Überraschung gegen 21

Um Phänomene zu untersuchen, die für die direkte Forschung zu komplex oder unzugänglich sind, verwenden Wissenschaftler Modelle. Nachdem sie im Labor ein Analogon eines Schwarzen Lochs erstellt haben, können sie möglicherweise etwas über das Verhalten von echten Schwarzen Löchern lernen, ohne am Rand des Ereignishorizonts entlang gehen zu müssen.

Mathematiker machen das Gleiche. Ein gutes Beispiel ist das Studium von Primzahlen. Mathematiker wollen die Antwort auf die Frage nach Zwillingsprimzahlen wissen - gibt es unendlich viele Primzahlenpaare, die sich um 2 unterscheiden (3 und 5, 11 und 13)? Eine erschöpfende Antwort geht über ihr Wissen hinaus, aber sie haben Modelle erstellt, die die Häufigkeit von Zwillingszahlen vorhersagen - und die Antwort scheint zu sein, dass sie unendlich oft vorkommen.

Das neue Modell untersucht die elliptischen Kurven selbst nicht direkt. Sie erforscht ein solches mathematisches Objekt wie den Matrixkern . Kerne beziehen sich auf elliptische Kurven, wie Mäuse für Menschen nicht dasselbe sind, aber sie sind leichter zu untersuchen, und es besteht die Hoffnung, dass sie nahe genug sind, um auf der Grundlage von Experimenten mit anderen Schlussfolgerungen über einige zu ziehen. Insbesondere haben Kernel ihre eigene Version des Ranges . Nachdem vier Mathematiker die Verteilung des Ranges der Kerne untersucht hatten - wie viele Kerne haben einen Rang von 1, wie viele Kerne einen Rang von 2 usw. -, hofften sie, eine Vorstellung von der Verteilung der Ränge der elliptischen Kurven zu bekommen. Tatsächlich wetten sie, dass die Verteilung der Reihen der Kerne und die elliptischen Kurven einander ähnlich sind.


Jennifer Park, Björn Puunen und Melanie Wood

"Der Sprung des Glaubens kommt ins Spiel", sagte Park. "Wir hoffen, dass es vielleicht einen anderen Satz mathematischer Objekte gibt, der viel verständlicher ist und die gleiche Rangverteilung wie elliptische Kurven hat."

Als die vier Forscher diese Arbeit machten, betrachteten die meisten Mathematiker den Rang als unbegrenzt. Das Modell erzählte jedoch eine andere Geschichte. Sie sagt, dass es nur eine endliche Anzahl von elliptischen Kurven mit einem Rang von mehr als 21 gibt. Und wenn es eine endliche Anzahl von ihnen gibt, hat einer von ihnen den höchsten Rang - was bedeutet, dass der Rang immer noch eine Obergrenze hat. Als die vier Mathematiker dies sahen, stellten sie fest, dass sie ein lebendiges Ergebnis in ihren Händen hatten.

"Diese Vorhersage stimmte nicht mit dem überein, woran alle glaubten, zumindest nicht mit dem, was sie öffentlich zugegeben hatten", sagte Wood. "Niemand glaubte, dass Ränge eine Einschränkung haben könnten."

Wenn das Vertrauen in das Modell einen ziemlich ernsthaften Schritt erfordert, ist ein noch größerer Schritt erforderlich, wenn das Modell meldet, dass der gesunde Menschenverstand falsch war. Es sprechen jedoch zahlreiche Beweise für dieses Ergebnis. Dieses Modell basiert auf früheren Modellen, die von anderen Mathematikern erstellt wurden, die verschiedene Eigenschaften elliptischer Kurven untersucht haben. Diese Modelle haben den Test der Zeit bestanden; Einige dieser Vorhersagen wurden sogar bewiesen.

"Niemand schlug vor, von vorne anzufangen und ein neues Modell zu bauen", sagte Wood. "Die Frage war, wie bestehende Modelle, an die die Menschen bereits glauben, bereichert werden können."

Ein weiterer Grund, an das Modell zu glauben, war, dass ein Rangwert von 21 keine willkürliche Grenze zu sein scheint. Zehn Jahre zuvor schuf Granville ein weiteres Modell, aus dem auch folgte, dass es nur eine begrenzte Anzahl von elliptischen Kurven mit einem Rang über 21 geben sollte. Das Granville-Modell war dem aktuellen Modell überhaupt nicht ähnlich - und die Tatsache, dass beide Rang 21 als signifikant gaben, war ganz anders als ein einfacher Zufall aus der Sicht vieler Mathematiker.

"Wir haben zwei völlig unterschiedliche heuristische Modelle und beide gaben die gleiche Zahl an, 21 - das hat die Leute überrascht", sagte Park.

Der vielleicht überzeugendste Grund, warum das Modell glaubwürdig erscheint, war die Tatsache, dass seine anderen Vorhersagen fast genau den nachgewiesenen Eigenschaften elliptischer Kurven entsprachen. Die verallgemeinerte Schlussfolgerung des Modells - das Vorhandensein einer endlichen Anzahl von elliptischen Kurven mit einem Rang von mehr als 21 - gilt für alle elliptischen Kurven. Sie haben jedoch bestimmte Familien, für die viele Mathematiker bereits die Grenzen der Ränge festgelegt haben. Das Modell sagte auch Rangwerte für viele dieser Familien voraus, und seine Vorhersagen waren ähnlich oder stimmten sogar genau mit den Grenzen überein, die Mathematiker bereits festgelegt haben.

"Unsere Grenzen haben all jene Fälle genau vorhergesagt, die von anderen Menschen untersucht wurden", sagte Park. "Die Leute stehen meinen Berichten skeptisch gegenüber, aber wenn ich andere Zufälle erwähne, sind sie darüber sehr überrascht."

Zwischen Beweis und Beweis

Das Modell hat viel Unterstützung, aber nicht jeder glaubt es, und es kann sich als falsch herausstellen. Der wichtigste Skeptiker ist Noam Elkis, ein Harvard-Mathematiker, der einen Rangrekord für eine elliptische Kurve aufgestellt hat. In den Jahrzehnten, seit er der jüngste Vollzeitprofessor in Harvard wurde, hat er mehrere Ergebnisse erhalten, die auf das Fehlen einer Ranggrenze hinweisen. "Meine Meinung hat sich seit langem nicht geändert - ich glaube nicht, dass wir uns in dieser Ausgabe gut auskennen, um eine bestimmte Hypothese zu stützen", schrieb Elkis mir per Post.

Elkis glaubt, dass das Modell in vielerlei Hinsicht möglicherweise nicht richtig funktioniert. Dabei werden zufällig ausgewählte Kurven berücksichtigt, oder Kurven sind in gewissem Sinne durchschnittlich. Es gibt jedoch Hinweise, einschließlich Untersuchungen von Elkis selbst, auf die Möglichkeit der Existenz von Familien elliptischer Kurven, von denen jede eine unendliche Anzahl solcher Kurven enthält, deren Verhalten sich erheblich vom Verhalten typischer Kurven unterscheidet. „Heuristische Modelle, die auf dem erwarteten Verhalten von Zufallskurven basieren, erzählen möglicherweise nicht die ganze Geschichte über extremes Verhalten“, schreibt Elkis.

Selbst einer der Autoren des Modells ist sich dessen nicht ganz sicher. "Ich würde sagen, dass ich in Reihen wie ein Agnostiker begrenzt bin", sagte Wood. Sie gibt zu, dass das Modell aus von Elkis geäußerten Gründen möglicherweise falsch ist. Wenn das Modell die Aufgabe jedoch nicht bewältigt, wurden einige versteckte und unerwartete Eigenschaften elliptischer Kurven nicht berücksichtigt. "Die Frage ist: Wenn Sie nicht an begrenzte Ränge glauben, an welchem ​​Ort funktioniert das Modell nicht mehr?" - sagte Wood.

„Höchstwahrscheinlich haben sie Recht, wenn sich jemand keinen genialen Grund einfallen lässt, warum sie sich irren. Ich habe keine Ahnung, ob es einen solchen Grund gibt oder nicht “, sagte Alexander Smith, ein Harvard-Doktorand, der mit Elkis zusammenarbeitet und die Reihen der elliptischen Kurven untersucht.

Die Autoren des Modells erheben seine Bedeutung für das Dogma nicht. Sie kennen den Unterschied zwischen Beweisen und Beweisen und sie verstehen, dass keine Berge der ersteren zu den letzteren führen werden. Sie glauben jedoch, dass ihre Arbeit zumindest nach einem Jahrhundert einfachen Denkens eine vernünftige Grundlage für die Reflexion grundlegender mathematischer Konzepte bietet.

"Vielleicht ist es für Mathematiker eine Herausforderung, elliptische Kurven höherer Ordnung zu finden", sagte Park. Oder vielleicht sollten Mathematiker "ihre Meinung über das, woran wir glaubten, als populäre Hypothese überdenken".