Hallo Wanderer. Wir als Reisende in unseren Gedanken und Analysatoren unseres Zustands sollten verstehen, wo es gut ist und wo sonst, wo genau wir sind, und ich möchte Leser dafür gewinnen.
Wie setzen wir nacheinander Gedanken-Ketten zusammen? Nehmen wir den Abschluss jedes Schritts an und steuern den Kontrollfluss und den Zustand der Zellen im Gedächtnis? Oder teilen Sie dem Programm einfach durch Beschreiben der Problemstellung mit, welche bestimmte Aufgabe Sie lösen möchten. Dies reicht aus, um alle Programme zu kompilieren. Verwandeln Sie die Codierung nicht in einen Strom von Befehlen, die den internen Status des Systems ändern, sondern drücken Sie das Prinzip als Konzept der Sortierung aus, da Sie sich nicht vorstellen müssen, welche Art von Algorithmus dort versteckt ist, sondern nur die sortierten Daten abrufen müssen. Nicht umsonst kann der Präsident von Amerika die Blase erwähnen, er drückt die Idee aus, dass er etwas in der Programmierung verstanden hat. Er hat gerade herausgefunden, dass es einen Sortieralgorithmus gibt und die Daten in der Tabelle auf seinem Desktop für sich genommen nicht auf magische Weise in alphabetischer Reihenfolge angeordnet werden können.
Diese Idee, dass ich der deklarativen Art, Gedanken auszudrücken und alles mit einer Folge von Befehlen und Übergängen zwischen ihnen auszudrücken, wohlgesonnen bin, scheint archaisch und veraltet zu sein, weil unsere Großväter dies getan haben, Großväter die Kontakte auf dem Patchfeld verdrahtet haben und die Lichter blinken ließen. und wir haben einen Monitor und eine Spracherkennung, da Sie auf dieser Entwicklungsstufe immer noch über das Befolgen von Befehlen nachdenken können ... Es scheint mir, dass wenn Sie das Programm in einer logischen Sprache ausdrücken, es verständlicher aussieht, und dies kann getan werden In der Technologie wurde bereits in den 80er Jahren eine Wette abgeschlossen.
Nun, die Einführung zog sich hin ...
Ich werde zunächst versuchen, den schnellen Sortiermechanismus erneut zu erzählen. Um eine Liste zu sortieren, müssen Sie sie in zwei Unterlisten unterteilen und die sortierte Unterliste mit einer anderen sortierten Unterliste kombinieren .
Die Aufteilungsoperation muss in der Lage sein, die Liste in zwei Unterlisten umzuwandeln, von denen eine alle weniger einfachen Elemente enthält und die zweite Liste nur große Elemente enthält. Um dies auszudrücken, werden auf Erlang nur zwei Zeilen geschrieben:
qsort([])->[]; qsort([H|T])->qsort([X||X<-T,X<H])++[H|qsort([X||X<-T,X>=H])].
Diese Ausdrücke des Ergebnisses des Denkprozesses interessieren mich.
Es ist schwieriger, das Sortierprinzip in zwingender Form zu beschreiben. Wie könnte diese Programmiermethode einen Vorteil haben, und dann nennt man sie nicht, obwohl es einen s-place-place gibt, zumindest einen fortran. Liegt es daran, dass Javascript und alle Trends der Lambda-Funktionen in den neuen Standards aller Sprachen eine Bestätigung für die Unannehmlichkeiten der Algorithmusizität sind?
Ich werde versuchen, ein Experiment durchzuführen, um die Vorteile eines Ansatzes und eines anderen zu überprüfen und zu testen. Ich werde versuchen zu zeigen, dass der deklarative Datensatz der Definition der Sortierung und sein algorithmischer Datensatz hinsichtlich der Leistung verglichen werden können, und daraus schließen, wie die Programme korrekter formuliert werden können. Vielleicht wird dies die Programmierung durch Algorithmen und den Fluss von Befehlen als einfach veraltete Ansätze, die für die Verwendung überhaupt nicht relevant sind, ins Regal rücken, weil es nicht weniger in Mode ist, sich in einem Haskell oder in einem Querschnitt auszudrücken. Und vielleicht kann nicht nur märchenscharf Programme einen klaren und kompakten Look verleihen?
Ich werde Python zur Demonstration verwenden, da es mehrere Paradigmen hat, und dies ist überhaupt nicht C ++ und ist nicht länger lisp. Sie können ein klares Programm in einem anderen Paradigma schreiben:
Sortieren 1
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<T])+[H]+qsort([X for X in T if X>=T])
Wörter können so gesprochen werden: Beim Sortieren wird das erste Element als Basis verwendet, und dann werden alle kleineren Elemente sortiert und mit allen größeren verbunden, bevor sie sortiert werden .
Oder vielleicht funktioniert ein solcher Ausdruck schneller als das Sortieren, das in der ungeschickten Form einer Permutation einiger Elemente in der Nähe geschrieben ist oder nicht. Ist es möglich, dies prägnanter auszudrücken und dafür nicht so viele Worte zu benötigen? Versuchen Sie, das Prinzip der Sortierung nach Blasen laut zu formulieren und dem Präsidenten der Vereinigten Staaten mitzuteilen, da er diese heiligen Daten erhalten hat, die Algorithmen kennengelernt und sie beispielsweise so ausgedrückt hat: Um die Liste zu sortieren, müssen Sie einige Elemente nehmen, sie miteinander vergleichen und Wenn die erste mehr als die zweite ist, müssen sie ausgetauscht und neu angeordnet werden. Anschließend müssen Sie die Suche nach Paaren solcher Elemente vom Anfang der Liste an wiederholen, bis die Permutationen beendet sind .
Ja, das Prinzip des Sortierens einer Blase klingt sogar länger als die schnelle Sortierversion, aber der zweite Vorteil liegt nicht nur in der Kürze des Datensatzes, sondern auch in seiner Geschwindigkeit. Ist der Ausdruck derselben vom Algorithmus formulierten schnellen Sortierung schneller als die deklarativ ausgedrückte Version? Vielleicht müssen wir unsere Ansichten zum Programmierunterricht ändern. Es ist notwendig, wie die Japaner versuchten, den Unterricht im Prolog und das damit verbundene Denken in den Schulen einzuführen. Sie können sich systematisch von den algorithmischen Ausdruckssprachen der Gedanken entfernen.
Sort 2
Um dies zu reproduzieren, musste ich mich der Literatur zuwenden. Dies ist eine Aussage von Hoar . Ich versuche, sie in Python umzuwandeln:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p - 1) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo - 1 j = hi + 1 while True do: i= i + 1 while A[i] < pivot do : j= j - 1 while A[j] > pivot if i >= j: return j A[i],A[j]=A[j],A[i]
Ich bewundere den Gedanken, dass hier ein endloser Zyklus benötigt wird, er hätte dort ein Go-That eingefügt)), da waren einige Joker.
Analyse
Lassen Sie uns nun eine lange Liste erstellen und nach beiden Methoden sortieren und verstehen, wie wir unsere Gedanken schneller und effizienter ausdrücken können. Welcher Ansatz ist einfacher zu verfolgen?
Wenn Sie eine Liste von Zufallszahlen als separates Problem erstellen, können Sie dies folgendermaßen ausdrücken:
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<H])+[H]+qsort([X for X in T if X>=H]) import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=qsort(list) print('qsort='+str(monotonic() - start))
Hier sind die erhaltenen Messungen:
>>> test(10000) qsort=0.046999999998661224 >>> test(10000) qsort=0.0629999999946449 >>> test(10000) qsort=0.046999999998661224 >>> test(100000) qsort=4.0789999999979045 >>> test(100000) qsort=3.6560000000026776 >>> test(100000) qsort=3.7340000000040163 >>>
Jetzt wiederhole ich dies in der Formulierung des Algorithmus:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p ) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo-1 j = hi+1 while True: while True: i=i+1 if(A[i]>=pivot) or (i>=hi): break while True: j=j-1 if(A[j]<=pivot) or (j<=lo): break if i >= j: return max(j,lo) A[i],A[j]=A[j],A[i] import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=quicksort(list,0,len-1) print('quicksort='+str(monotonic() - start))
Ich musste daran arbeiten, das ursprüngliche Beispiel des Algorithmus von alten Quellen in Wikipedia umzuwandeln. Also das: Sie müssen das unterstützende Element nehmen und die Elemente im Subarray so anordnen, dass immer weniger links und immer mehr rechts ist. Tauschen Sie dazu das linke mit dem rechten Element aus. Wir wiederholen dies für jede Unterliste des Referenzelements geteilt durch den Index. Wenn nichts zu ändern ist, beenden wir den Vorgang .
Insgesamt
Mal sehen, wie groß der Zeitunterschied für dieselbe Liste ist, die nacheinander nach zwei Methoden sortiert ist. Wir werden 100 Experimente durchführen und ein Diagramm erstellen:
import random def test(len): t1,t2=[],[] for n in range(1,100): list=[random.randint(-100, 100) for r in range(0,len)] list2=list[:] from time import monotonic start = monotonic() slist=qsort(list) t1+=[monotonic() - start]
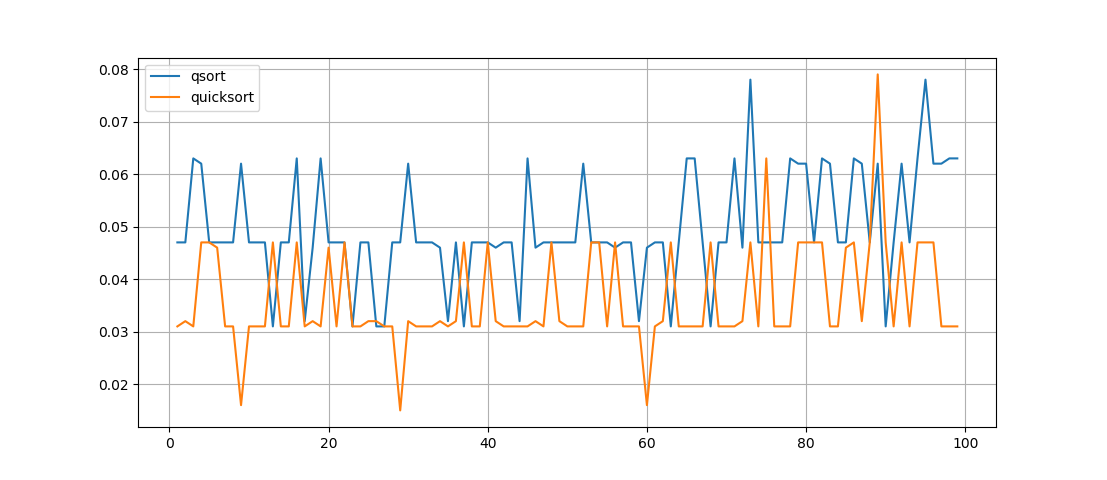
Was hier zu sehen ist - die Funktion quicksort () arbeitet schneller , aber ihre Aufzeichnung ist nicht so offensichtlich, obwohl die Funktion rekursiv ist, aber es ist überhaupt nicht leicht, die Arbeit der darin ausgeführten Permutationen zu verstehen.
Welcher Ausdruck des Sortierens von Gedanken ist bewusster?
Mit einem kleinen Unterschied in der Leistung erhalten wir einen solchen Unterschied in der Menge und Komplexität des Codes.
Vielleicht reicht die Wahrheit aus, um zwingende Sprachen zu lernen, aber was ist für Sie attraktiver?
PS. Und hier ist der Prolog:
qsort([],[]). qsort([H|T],Res):- findall(X,(member(X,T),X<H),L1), findall(X,(member(X,T),X>=H),L2), qsort(L1,S1), qsort(L2,S2), append(S1,[H|S2],Res).