Modernes DDR3 SDRAM. Quelle: BY-SA / 4.0 von KjerishWährend eines kürzlichen Besuchs
im Computer History Museum in Mountain View machte mich eine alte Probe des
Ferritgedächtnisses auf sich aufmerksam.
Quelle: BY-SA / 3.0 von Konstantin LanzetIch kam schnell zu dem Schluss, dass ich keine Ahnung habe, wie solche Dinge funktionieren. Drehen sich die Ringe (nein) und warum gehen drei Drähte durch jeden Ring (ich verstehe immer noch nicht, wie sie funktionieren). Noch wichtiger ist, dass ich sehr wenig Ahnung habe, wie der moderne dynamische RAM funktioniert!
Quelle: Ulrich Drappers GedächtniszyklusIch war besonders an einer der Konsequenzen interessiert, wie dynamisches RAM funktioniert. Es stellt sich heraus, dass jedes Datenbit durch eine Ladung (oder deren Abwesenheit) auf einem winzigen Kondensator im RAM-Chip gespeichert wird. Diese Kondensatoren verlieren jedoch mit der Zeit allmählich ihre Ladung. Um den Verlust gespeicherter Daten zu vermeiden, müssen diese regelmäßig aktualisiert werden, um die Gebühr (falls vorhanden) auf ihren ursprünglichen Stand zurückzusetzen. Bei diesem
Aktualisierungsvorgang wird jedes Bit gelesen und anschließend zurückgeschrieben. Während dieser „Aktualisierung“ ist der Speicher belegt und kann keine normalen Vorgänge wie das Schreiben oder Speichern von Bits ausführen.
Das hat mich lange gestört und ich habe mich gefragt ... ist es möglich, eine Verzögerung bei der Aktualisierung auf Programmebene zu bemerken?
Dynamic RAM Upgrade Training Base
Jedes DIMM besteht aus "Zellen" und "Zeilen", "Spalten", "Seiten" und / oder "Rängen".
Diese Präsentation der University of Utah erklärt die Nomenklatur. Die Konfiguration des Computerspeichers kann mit dem
decode-dimms überprüft werden. Hier ist ein Beispiel:
$ decode-dimms
Größe 4096 MB
Bänke x Zeilen x Spalten x Bits 8 x 15 x 10 x 64
Ränge 2
Wir müssen nicht das gesamte DDR-DIMM-Schema verstehen, sondern die Funktionsweise nur einer Zelle verstehen, in der ein Informationsbit gespeichert ist. Genauer gesagt interessiert uns nur der Update-Prozess.
Betrachten Sie zwei Quellen:
Jedes Bit im dynamischen Speicher muss aktualisiert werden: Dies geschieht normalerweise alle 64 ms (das sogenannte statische Update). Dies ist eine ziemlich teure Operation. Um alle 64 ms einen größeren Stopp zu vermeiden, ist der Prozess in 8192 kleinere Aktualisierungsvorgänge unterteilt. In jedem von ihnen sendet der Speichercontroller des Computers Aktualisierungsbefehle an DRAM-Chips. Nach Erhalt der Anweisungen aktualisiert der Chip 1/8192 Zellen. Wenn Sie zählen, sind 64 ms / 8192 = 7812,5 ns oder 7,81 μs. Dies bedeutet Folgendes:
- Ein Aktualisierungsbefehl wird alle 7812,5 ns ausgeführt. Es heißt tREFI.
- Der Aktualisierungs- und Wiederherstellungsprozess dauert einige Zeit, sodass der Chip wieder normale Lese- und Schreibvorgänge ausführen kann. Der sogenannte tRFC entspricht entweder 75 ns oder 120 ns (wie in der erwähnten Micron-Dokumentation).
Wenn der Speicher heiß ist (über 85 ° C), verringert sich die Datenspeicherzeit im Speicher und die statische Aktualisierungszeit wird auf 32 ms halbiert. Dementsprechend fällt tREFI auf 3906,25 ns.
Ein typischer Speicherchip ist für einen wesentlichen Teil seiner Lebensdauer mit der Aktualisierung beschäftigt: von 0,4% auf 5%. Darüber hinaus sind Speicherchips für den nicht trivialen Anteil des Stromverbrauchs eines typischen Computers verantwortlich, und der größte Teil dieser Energie wird für Upgrades aufgewendet.
Der gesamte Speicherchip wird während des Updates blockiert. Das heißt, jedes Bit im Speicher wird alle 7812 ns für mehr als 75 ns gesperrt. Lassen Sie es uns messen.
Versuchsvorbereitung
Um Operationen mit einer Genauigkeit von Nanosekunden zu messen, benötigen Sie einen sehr engen Zyklus, möglicherweise in C. Es sieht folgendermaßen aus:
for (i = 0; i < ...; i++) {
Der vollständige Code ist auf GitHub verfügbar.Der Code ist sehr einfach. Führen Sie eine Speicherlesung durch. Wir sichern Daten aus dem CPU-Cache. Wir messen die Zeit.
(Hinweis: Im
zweiten Experiment habe ich versucht, MOVNTDQA zum Laden von Daten zu verwenden, dies erfordert jedoch eine spezielle nicht zwischenspeicherbare Speicherseite und Root-Rechte.)
Auf meinem Computer zeigt das Programm die folgenden Daten an:
# Zeitstempel, Zykluszeit
3101895733, 134
3101895865, 132
3101896002, 137
3101896134, 132
3101896268, 134
3101896403, 135
3101896762, 359
3101896901, 139
3101897038, 137
Üblicherweise wird ein Zyklus mit einer Dauer von ungefähr 140 ns erhalten, periodisch springt die Zeit auf ungefähr 360 ns. Manchmal tauchen über 3200 ns seltsame Ergebnisse auf.
Leider sind die Daten zu verrauscht. Es ist sehr schwer zu erkennen, ob mit Aktualisierungszyklen eine merkliche Verzögerung verbunden ist.
Schnelle Fourier-Transformation
Irgendwann dämmerte es mir. Da wir ein Ereignis mit einem festen Intervall finden möchten, können wir Daten an den FFT-Algorithmus (schnelle Fourier-Transformation) senden, der die Hauptfrequenzen entschlüsselt.
Ich bin nicht der erste, der darüber nachdenkt: Mark Seaborn mit der berühmten Sicherheitslücke
Rowhammer hat diese Technik bereits 2015 implementiert. Selbst nachdem ich mir Marks Code angesehen hatte, war es schwieriger als erwartet, FFT zum Laufen zu bringen. Aber am Ende habe ich alle Teile zusammengefügt.
Zuerst müssen Sie die Daten vorbereiten. FFT erfordert eine Eingabe mit einem konstanten Abtastintervall. Wir möchten auch die Daten kürzen, um das Rauschen zu reduzieren. Durch Versuch und Irrtum stellte ich fest, dass das beste Ergebnis nach vorläufiger Verarbeitung der Daten erzielt wird:
- Kleine Werte (weniger als 1,8 Durchschnitt) von Schleifeniterationen werden abgeschnitten, ignoriert und durch Nullen ersetzt. Wir wollen wirklich keinen Lärm machen.
- Alle anderen Messwerte werden durch Einheiten ersetzt, da die Amplitude der Verzögerung, die durch etwas Rauschen verursacht wird, für uns wirklich nicht wichtig ist.
- Ich habe mich für ein Abtastintervall von 100 ns entschieden, aber jede Zahl bis zur Nyquist-Frequenz (doppelte erwartete Frequenz) reicht aus .
- Die Daten müssen zu einem festgelegten Zeitpunkt abgetastet werden, bevor sie an die FFT übermittelt werden. Alle vernünftigen Abtastmethoden funktionieren einwandfrei. Ich habe mich für die grundlegende lineare Interpolation entschieden.
Der Algorithmus ist ungefähr so:
UNIT=100ns A = [(timestamp, loop_duration),...] p = 1 for curr_ts in frange(fist_ts, last_ts, UNIT): while not(A[p-1].timestamp <= curr_ts < A[p].timestamp): p += 1 v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0 v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0 v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp) B.append( v )
Was auf meinen Daten einen ziemlich langweiligen Vektor wie diesen erzeugt:
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...]
Der Vektor ist jedoch ziemlich groß, normalerweise ungefähr 200.000 Datenpunkte. Mit solchen Daten können Sie FFT verwenden!
C = numpy.fft.fft(B) C = numpy.abs(C) F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)
Ziemlich einfach, oder? Dies erzeugt zwei Vektoren:
- C enthält eine komplexe Anzahl von Frequenzkomponenten. Wir sind nicht an komplexen Zahlen interessiert, und Sie können sie mit dem Befehl
abs() glätten. - F enthält Beschriftungen, deren Frequenzspanne an welcher Stelle des Vektors C liegt. Wir normalisieren den Exponenten auf Hertz, indem wir ihn mit der Abtastfrequenz des Eingangsvektors multiplizieren.
Das Ergebnis kann in einem Diagramm dargestellt werden:
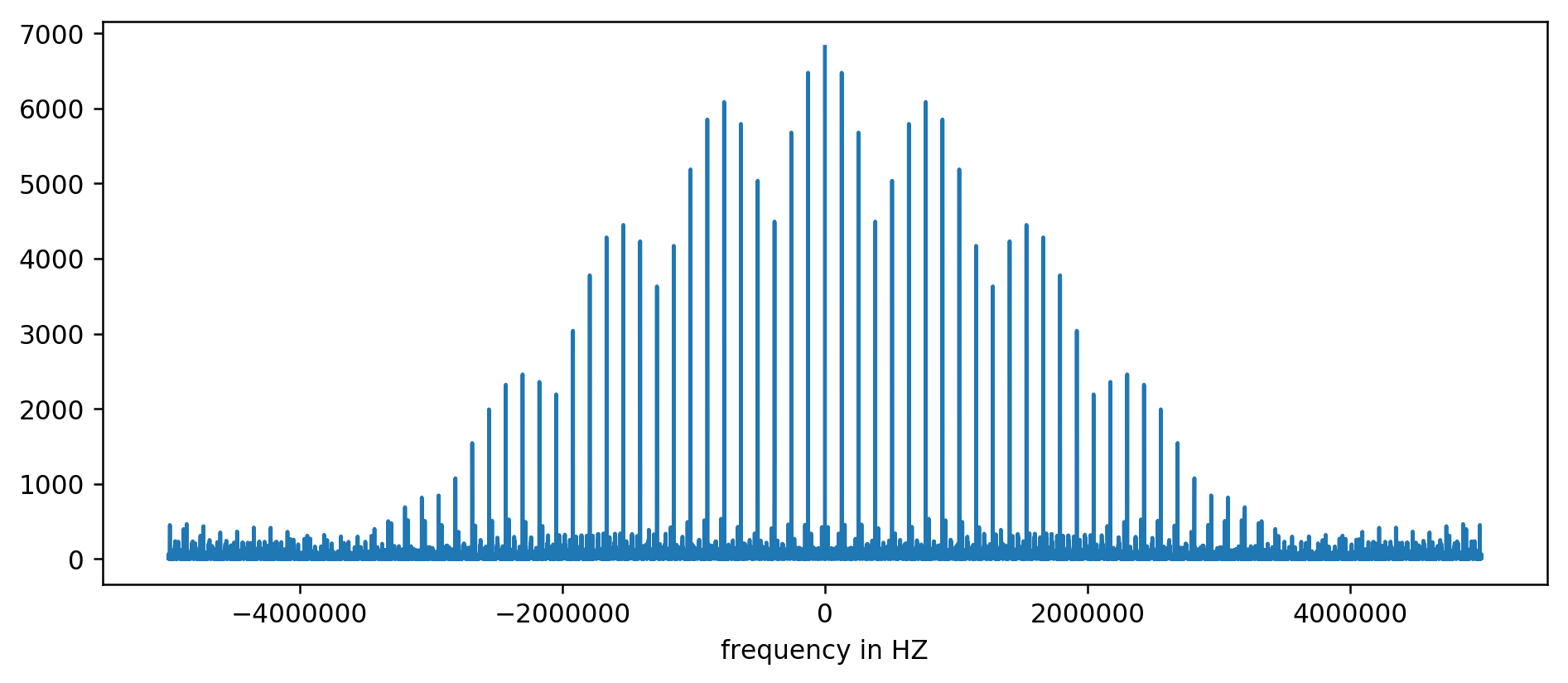
Y-Achse ohne Einheiten, da wir die Verzögerungszeit normalisiert haben. Trotzdem sind Bursts in einigen festen Frequenzbereichen deutlich sichtbar. Betrachten wir sie näher:
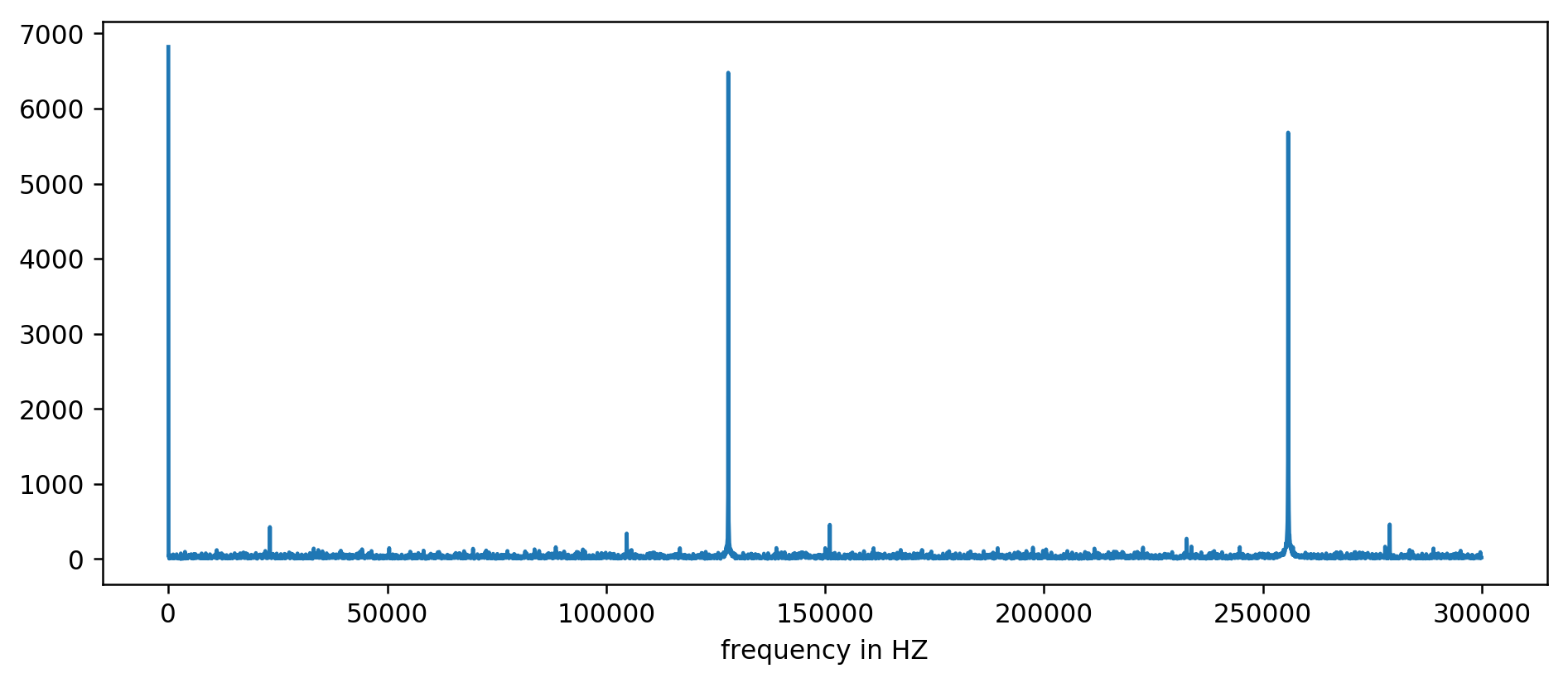
Wir sehen deutlich die ersten drei Gipfel. Nach ein wenig unaussprechlicher Arithmetik, einschließlich des Filterns des mindestens zehnfachen Durchschnittswerts, können Sie die Grundfrequenzen extrahieren:
127850.0
127900.0
127950.0
255700.0
255750.0
255800.0
255850.0
255900.0
255950.0
383600.0
383650.0
Wir betrachten: 1000000000 (ns / s) / 127900 (Hz) = 7818,6 ns
Hurra! Der erste Frequenzsprung ist genau das, wonach wir gesucht haben, und er korreliert wirklich mit der Aktualisierungszeit.
Die verbleibenden Spitzen bei 256 kHz, 384 kHz, 512 kHz sind die sogenannten Harmonischen, die ein Vielfaches unserer Grundfrequenz von 128 kHz sind. Dies ist der vollständig erwartete Nebeneffekt der
Anwendung von FFT auf so etwas wie eine Rechteckwelle .
Um die Experimente zu vereinfachen, haben wir eine
Version für die Befehlszeile erstellt . Sie können den Code selbst ausführen. Hier ist ein Beispiel für den Start auf meinem Server:
~ / 2018-11-memory-refresh $ make
gcc -msse4.1 -ggdb -O3 -Wand -Wextra Measure-Dram.c -o Measure-Dram
./measure-dram | python3 ./analyze-dram.py
[*] Überprüfen der ASLR: main = 0x555555554890 stack = 0x7fffffefe2ec
[] Lustige Tatsache. Ich habe 40663553 clock_gettime () pro Sekunde gemacht
[*] Messung der MOVQ + CLFLUSH-Zeit. Ausführen von 131072-Iterationen.
[*] Daten ausschreiben
[*] Eingabedaten: min = 117 avg = 176 med = 167 max = 8172 items = 131072
[*] Grenzbereich 212-inf
[] 127849 Elemente unterhalb des Grenzwerts, 0 Elemente oberhalb des Grenzwerts, 3223 Elemente ungleich Null
[*] FFT ausführen
[*] Die Spitzenfrequenz über 2 kHz unter 250 kHz hat eine Stärke von 7716
[+] Spitzenfrequenzspitzen über 2 kHz liegen bei:
127906Hz 7716
255813Hz 7947
383720Hz 7460
511626Hz 7141
Ich muss zugeben, der Code ist nicht ganz stabil. Bei Problemen wird empfohlen, Turbo Boost, CPU-Frequenzskalierung und Leistungsoptimierung zu deaktivieren.
Fazit
Es gibt zwei Hauptschlussfolgerungen aus dieser Arbeit.
Wir haben gesehen, dass Low-Level-Daten ziemlich schwer zu analysieren sind und ziemlich verrauscht erscheinen. Anstatt mit bloßem Auge zu bewerten, können Sie immer die gute alte FFT verwenden. Bei der Aufbereitung der Daten ist gewissermaßen Wunschdenken erforderlich.
Vor allem haben wir gezeigt, dass es oft möglich ist, subtiles Hardwareverhalten anhand eines einfachen Prozesses im Benutzerbereich zu messen. Diese Art des Denkens führte zur Entdeckung der
ursprünglichen Rowhammer-Sicherheitslücke . Sie wurde in den Meltdown / Spectre-Angriffen implementiert und erneut in der jüngsten
Rowhammer-Reinkarnation für ECC-Speicher gezeigt .
Vieles geht über den Rahmen dieses Artikels hinaus. Wir haben den internen Betrieb des Speichersubsystems kaum berührt. Zur weiteren Lektüre empfehle ich:
Zum Schluss noch eine gute Beschreibung des alten Ferritspeichers: