Neue Erkenntnisse belegen die Existenz von zwei Arten von unendlichen Kurven

Die Arbeit von Alexander Smith an der Goldfeld-Hypothese enthüllte die grundlegenden Eigenschaften elliptischer Kurven

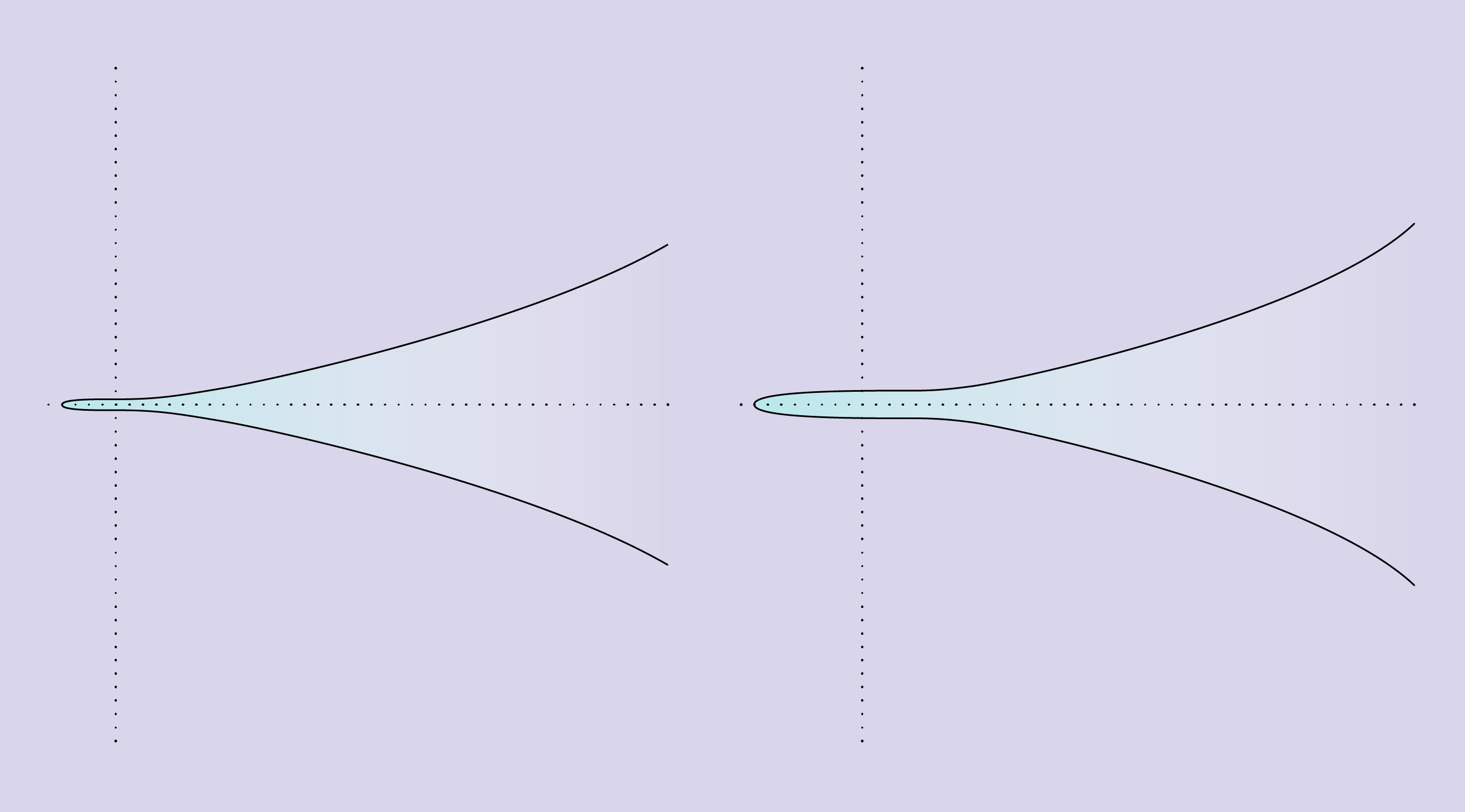Zwei elliptische Kurven zeigen die Seltsamkeit des Rangbegriffs. Die Kurve links wird durch die Gleichung y ² = x ³ + 1 beschrieben, durchläuft nur fünf rationale Punkte und hat Rang 0. Die Kurve rechts wird durch die Gleichung y ² = x ³ + 8 beschrieben, durchläuft eine unendliche Anzahl rationaler Punkte und hat Rang 1.

Es kann viele Varianten von elliptischen Kurven geben, aber es gibt nur zwei ihrer realen Varianten. Dies ist das Ergebnis der neuen Erkenntnisse, die ein Doktorand der Harvard University erhalten hat.

Elliptische Kurven wirken exotisch, aber dies sind unauffällige geometrische Objekte, die nicht komplizierter sind als gerade Linien, Parabeln oder Ellipsen. In seiner im letzten Jahr online veröffentlichten Arbeit hat Alexadr Smith die Hypothese von vor vierzig Jahren bezüglich des grundlegenden Merkmals elliptischer Rangkurven bewiesen. Smith hat bewiesen, dass von einer gegebenen Kurvenfamilie mit einer Eigenschaft die Hälfte einen Rang von 0 und die Hälfte einen Rang von 1 hat.

Dieses Ergebnis legt ein unterstützendes Merkmal von Objekten fest, die Mathematiker seit vielen Jahrhunderten beschäftigen und deren Bedeutung in den letzten Jahrzehnten besonders zugenommen hat.

„Wir haben mehr als 1000 Jahre darüber nachgedacht und jetzt haben wir ein probabilistisches Verständnis für elliptische Kurven. Dies ist äußerst wichtig “, sagte Shaw-U Zhang , ein Mathematiker an der Princeton University, der Smith Empfehlungen zu seiner Arbeit gab, als er noch Student in Princeton war.

Elliptische Kurven sind Gleichungen mit Variablen, die auf die dritte Potenz angehoben werden, z. B. y ² = x ³ + 1. Sie sind in den letzten Jahrzehnten in vielen bedeutenden mathematischen Beweisen aufgetaucht, einschließlich des wichtigsten Beweises für Fermats Großen Satz von 1994. Ein Teil ihrer Bedeutung liegt in der Tatsache, dass sie zu den komplexesten Polynomgleichungen gehören, über die Mathematiker systemische Vorstellungen haben.

"Elliptische Kurven sind ein interessanter Fall", sagte Dorian Goldfeld , Mathematiker an der Columbia University, der 1979 eine Hypothese vorschlug, die seinen Namen erhielt.

Die Goldfeld-Hypothese macht Vorhersagen über den Rang elliptischer Kurven. Wie wir bereits in einem kürzlich erschienenen Artikel beschrieben haben: „ Welche Beweise können Mathematiker überzeugen, wenn es keinen strengen Beweis gibt? “ Der Rang ist ein Maß für die Komplexität einer Reihe rationaler Lösungen einer Kurve (Lösungen, die als Brüche dargestellt werden können). Und obwohl es keine nachgewiesene Einschränkung für den Rang der Kurve gibt - bisher wird der 28 höchste als der höchste Rang angesehen -, sagt die Goldfeld-Hypothese voraus, dass im Durchschnitt die Hälfte der elliptischen Kurven einen Rang von 0 und die andere Hälfte 1 hat.

Es mag Ihnen nicht klar erscheinen, wie elliptische Kurven mit einem Rang von mehr als 1 existieren können, wenn die Hälfte der elliptischen Kurven einen Rang von 0 und die andere Hälfte 1 hat. Wenn Sie eine Schachtel mit Tischtennisbällen haben und wenn Sie genau die Hälfte von kennen Sie sind schwarz und die Hälfte weiß, dann kann es keine roten geben.

Noch verwirrender ist die Tatsache, dass elliptische Kurven mit einem Rang von 2 oder höher nicht nur wenige, sondern eine unendliche Zahl existieren. Das scheinbar absurde Ergebnis ist das Ergebnis gerissener Statistiken, die mit Unendlichkeiten arbeiten. Obwohl es viele Kurven mit Rang 2 und höher gibt, gibt es so viele Kurven mit Rang 0 und 1, dass Kurven mit Rang 2 und höher statistisch nicht signifikant sind. Wenn Sie alle Kurven in eine Box legen und sie zufällig herausnehmen, ist die Wahrscheinlichkeit, eine Kurve mit einem Rang von mehr als 1 herauszuziehen, offiziell gleich Null.

Was bedeutet es, dass der Rang der Kurve 0 ist? Solche Kurven haben eine endliche Anzahl rationaler Punkte - und nicht mehr als 16, wie Barry Mazur in den 1970er Jahren bewiesen hat.


Dorian Goldfeld

Es gibt Gründe zu der Annahme, dass eine sehr große Anzahl von elliptischen Kurven einen Rang von 0 hat. Wenn Sie sich vorstellen, wie eine Kurve entlang einer Ebene verläuft, werden Sie feststellen, dass die meisten Punkte, durch die sie verläuft, nicht rational sind. Diese Punkte können nicht als Brüche ausgedrückt werden, selbst wenn sie beliebig komplex sind. Die Wahrscheinlichkeit, dass eine zufällige Kurve viele rationale Punkte schneidet - eine unendliche Menge - ist gering.

"Ich verstehe das so: Wenn Sie eine zufällige elliptische Kurve nehmen, hat dies Gründe für einen Rang von 0. Sie möchte keine rationalen Punkte haben", sagte Smith.

Die Prävalenz von Rang-1-Kurven wird auf ähnliche Weise erklärt. Rang 1-Kurven haben unendlich viele rationale Punkte, aber alle sind sehr ordentlich ausgerichtet, so dass Sie sie in einem ziemlich einfachen Prozess miteinander verbinden können.

Für Kurven mit Rang 2 und höher sind die Sätze rationaler Punkte komplizierter. Sie enthalten mehrere unendliche Teilmengen rationaler Punkte, die nicht miteinander verbunden sind.

„Wie stehen die Chancen, dass zwei unabhängige Punkte auftreten? - sagte Goldfeld. "Sehr niedrig." Meine Hypothese besagt, dass dies selten passieren sollte. “

Als Goldfeld seine Hypothese zum ersten Mal aufstellte, hielten die meisten Mathematiker sie für falsch. Sie wiesen auf die Ergebnisse von Computerexperimenten hin, aus denen hervorgeht, dass Kurven mit einem Rang von 2 oder höher viel häufiger auftreten als in 0% der Fälle.

Goldfeld antwortete, dass sie die Reichweite einfach zu klein nehmen. Er wies darauf hin, dass man, wenn man nur die ersten 10 ganzen Zahlen studiert, eine äußerst ungenaue Schätzung erhalten kann, dass 40% der Zahlen Primzahlen sind. In ähnlicher Weise wurden diese Computerexperimente von kleinen Teilmengen elliptischer Kurven auf unendlich große Kurvenfamilien extrapoliert.

„Ich sagte, schau dir die Primzahlen an! Das war meine Antwort. Wir müssen viel höher klettern, weil am Anfang viel Spaß auftauchen kann “, sagte Goldfeld.

Die Goldfeld-Hypothese gilt nicht für alle elliptischen Kurven. Es beschreibt eine spezielle Familie von elliptischen Kurven, quadratischen Drehungen. Beispiel: elliptische Kurve cy ² = x ³ - x, wobei c eine Konstante ist. Durch Ändern des Werts von c biegen Sie eine elliptische Kurve. Die Goldfeld-Hypothese bezieht sich auf die gesamte unendliche Vielfalt von Kurven, die durch Ändern des Wertes von c erhalten werden können.

Alexander Smith sagte aus, dass Goldfeld Recht hatte. In einer neuen Arbeit beweist er, dass 100% der elliptischen Kurven (einer besonderen Art) einen Rang von 0 oder 1 haben. Er hat auch bewiesen, dass diese Kurven gleichmäßig zwischen den beiden Rängen aufgeteilt sind, obwohl es einen Haken gibt. Sein Beweis für die 50-50-Teilung basiert auf der Gültigkeit der Birch-Swinnerton-Dyer (BJD) -Hypothese . Die BSD-Hypothese ist eines der bekanntesten offenen Probleme in der Mathematik. Mathematiker sind dem Beweis noch nicht nahe gekommen, aber im Großen und Ganzen halten sie ihn für wahr.

Trotz dieser Einschränkung wird Smiths Ergebnis als signifikant angesehen. Mathematiker sagen, dass er einen Weg zeigt, die Goldfeld-Hypothese vollständig zu beweisen, ohne sich mit der entmutigenden BSD-Hypothese zu messen. Diese Methode gibt ein neues Verständnis der Natur elliptischer Kurven.

"Alex Smiths Arbeit ist äußerst interessant, und ich denke, sie muss noch studiert und gegeben werden, was sie verdient", sagte Melanie Wood , Mathematikerin an der Universität von Wisconsin. "Die Tatsache, dass dies bewiesen werden kann, ist sehr wichtig und revolutionär."