Eine praktische Implementierung des Schaltgenerators mit Verilog HDL

Zusammenfassung

Schieberegister mit linearer Rückkopplung sind ein hervorragendes Werkzeug zur Implementierung eines Pseudozufallsbitgenerators in Hardware. Sie verhindern eine einfache und effiziente elektronische Struktur. Darüber hinaus sind sie in der Lage, Ausgabesequenzen mit großen Perioden und guten statistischen Eigenschaften zu erzeugen. Standard-LFSRs sind jedoch nicht kryptografisch sicher, da die Ausgabesequenz bei einer kleinen Anzahl von Schlüsselstrombits unter Verwendung des Berlekamp-Massey-Algorithmus eindeutig vorhergesagt werden kann. Es wurden verschiedene Methoden vorgeschlagen, um die dem LFSR-Design innewohnende Linearität zu zerstören. Diese Verfahren umfassen nichtlineare Kombinationsgeneratoren, nichtlineare Filtergeneratoren und taktgesteuerte Generatoren. Trotzdem bleiben sie anfällig für viele Angriffe wie Seitenkanalangriffe und algebraische Angriffe. Im Jahr 2015 wurde ein neuer getakteter gesteuerter Generator namens Schaltgenerator vorgeschlagen. Dieser neue Generator ist nachweislich resistent gegen algebraische Angriffe und Seitenkanalangriffe, während die Effizienz- und Sicherheitsanforderungen erhalten bleiben. In diesem Projekt präsentieren wir ein Design des Schaltgenerators mit Verilog HDL.

Einführung und historischer Hintergrund

Die Geschichte der Erzeugung von Pseudozufallszahlen in Hardware ist stark mit der Entwicklung von Stream-Chiffren verbunden. Stream-Chiffren sind Chiffren, die Klartextzeichen einzeln (normalerweise Stück für Stück) verschlüsseln, im Gegensatz zu Blockchiffren, die Klartext in großen Blöcken (64 Bit oder mehr) verschlüsseln. Viele Stream-Verschlüsselungsarchitekturen erfordern einen Schlüsselstromgenerator, bei dem es sich um einen Pseudozufallsbitgenerator handelt, dessen Startwert der Verschlüsselungsschlüssel ist. Für jedes Klartextbit wird das entsprechende Chiffretextbit als eine umkehrbare Funktion (normalerweise xor gate) des Klartextbits und des entsprechenden Schlüsselstrombits berechnet. Daher ist das Entwerfen sicherer und effizienter Schlüsselstromgeneratoren für den Betrieb der Stromverschlüsselung von wesentlicher Bedeutung.


Ein nützliches Werkzeug zum Erstellen von Schlüsselstromgeneratoren sind lineare Rückkopplungsschieberegister. Sie können einfach mit elementaren elektronischen Bauteilen konstruiert und einfach auf programmierbaren Logikbausteinen programmiert werden. Aufgrund ihrer einfachen Struktur können LFSRs auch mathematisch modelliert und analysiert werden, was zu einer Vielzahl von Kenntnissen und Ergebnissen in Bezug auf sie geführt hat. Die Ausgabesequenz eines korrekt konstruierten LFSR weist eine exponentielle Länge und gute statistische Eigenschaften wie eine große lineare Komplexität auf.


Trotz der guten statistischen Eigenschaften des LFSR kann es aufgrund seiner linearen Natur nicht als Schlüsselstromgenerator in seiner Standardform verwendet werden. Wenn ein Angreifer es geschafft hat zu wissen $$$2L$aufeinanderfolgende Schlüsselstrombits, dann kann die Ausgabesequenz unter Verwendung des Berlekamp-Massey-Algorithmus eindeutig und effizient vorhergesagt werden, wobei $$$L$ist die Anzahl der Register. Es wurden viele verschiedene Möglichkeiten vorgeschlagen, um die der LFSR-Ausgabesequenz inhärente Linearität zu zerstören:

• Verwendung mehrerer LFSRs und einer nichtlinearen Kombinationsfunktion ihrer Ausgänge (nichtlineare Kombinationsgeneratoren).
• Generieren der Ausgabesequenz als eine nichtlineare Funktion des LFSR-Zustands (nichtlineare Filtergeneratoren).
• Unregelmäßiges Takten von LFSRs (taktgesteuerten Generatoren).

Trotzdem blieben alle diese Designs anfällig für Angriffe wie algebraische Angriffe und Seitenkanalangriffe. Nach dem Jahr 2000 war dies kein kritisches Thema mehr, da die Blockverschlüsselung Rijndael als Advanced Encryption Standard (AES) vorgeschlagen und gewählt wurde. AES war in der Lage, im Stream-Verschlüsselungsmodus zu arbeiten und alle industriellen Standards für eine Stream-Verschlüsselung zu erfüllen. Darüber hinaus könnte AES mit zunehmender Rechenleistung auf verschiedenen Plattformen eingesetzt werden. Dies hat zu einer signifikanten Verringerung der Stream-Verschlüsselungsanwendungen geführt.


Adi Shamir hielt in Stream Ciphers 2004 und Asiacrypt 2004 einen eingeladenen Vortrag mit dem Titel "Stream Ciphers: Dead or Alive?". In seiner Präsentation schlug er vor, dass Stream-Chiffren in den folgenden Anwendungen überleben können:

• Softwareorientierte Anwendungen mit außergewöhnlich hohen Geschwindigkeiten (z. B. Router).
• Hardwareorientierte Anwendungen mit außergewöhnlich geringem Platzbedarf (z. B. Smartcards).

Einer der neuesten Vorschläge für Schlüsselstromgeneratoren ist der Schaltgenerator. Es soll gegen algebraische und Seitenkanalangriffe resistent sein und gleichzeitig die Effizienz und die Betriebsgeschwindigkeit erhalten.


In diesem Projekt werden wir einen Entwurf des Schaltgenerators in Hardware unter Verwendung von Verilog HDL vorstellen. Zunächst stellen wir die beiden gängigen Formen von LFSRs vor, Fibonacci-LFSRs und Galois-LFSRs. Als nächstes präsentieren wir eine mathematische Darstellung von LFSRs. Wir werden dann den Schaltgenerator wie von vorgestellt vorstellen. Abschließend stellen wir unser Verilog-Design des Schaltgenerators vor.

Schieberegister mit linearer Rückkopplung

Lineare Rückkopplungsschieberegister sind Schaltungen, die aus einer linearen Liste von Registern (auch Verzögerungselemente genannt) und einem vordefinierten Satz von Verbindungen zwischen ihnen bestehen. Ein globales (einzelnes) Taktsignal steuert den Datenfluss innerhalb des LFSR. Die beiden am häufigsten verwendeten Arten von LFSRs sind Fibonacci-LFSRs und Galois-LFSRs. nur in Form von Verbindungen aufschieben. Wie wir später im Abschnitt über mathematische Modelle sehen werden, gibt es viele Ähnlichkeiten zwischen Fibonacci-Architekturen und Galois-Architekturen, wobei es anwendungsspezifisch ist, eine der anderen vorzuziehen.


In diesem Artikel nehmen wir einen hypothetischen globalen Zeitzähler an, der bei beginnt $$$0$und zunehmen um $$$1$nach jeder positiven Flanke des globalen Taktzyklus.

Register

Ein Register ist ein Logikelement, das ein Datenbit speichern kann, das als Zustand bezeichnet wird. Es hat zwei Eingangsleitungen: eine Ein-Bit-Datenleitung und eine Taktsignalleitung. Es hat eine Ein-Bit-Ausgabe, die immer dem internen Zustand entspricht. Bei jeder positiven Flanke des Takteingangs wird der Dateneingang dem Zustand zugewiesen, andernfalls bleibt der Zustand unverändert. Bezeichnen wir den Zustand eines Registers $$$S$zur Zeit $$$t$als $$$\ mathop S \ nolimits ^ t$.

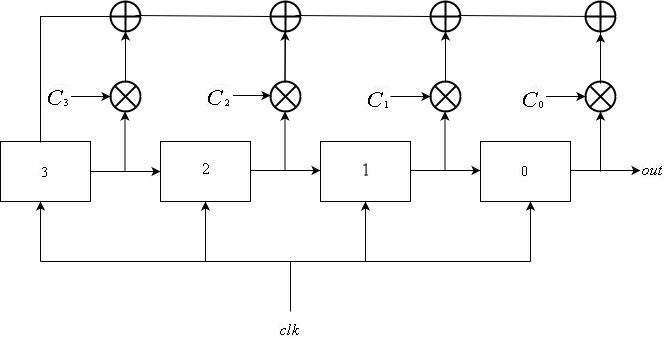
Fibonacci lfsrs

Ein Fibonacci LFSR besteht aus $$$L$Register aufgezählt von $$$0$zu $$$L-1$, alle mit dem gleichen Taktsignal verbunden. Die Eingabe des Registers $$$i$ist die Ausgabe des Registers $$$i + 1$für $$$0 \ le i \ le L-2$. Der Feedback-Eingang für das Register $$$L-1$ist die xoder Summe der Ausgänge einer Teilmenge von Registern. Die Registeraktualisierung kann mathematisch wie folgt beschrieben werden:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i + 1} ^ {t-1} {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ rm {if} \ \} 0 \ le i \ le L-2 \\ \ mathop \ bigoplus \ limit_ {j = 1} ^ k \ mathop S \ nolimits_j ^ {t-1} \ otimes \ mathop C \ nolimits_j {\ \ \ \ \ rm {if} \ \} i = L-1 \ end {array} \ right.$$

wo $$$C_j = 1$wenn registrieren $$$j$ist im Feedback enthalten und $$$0$sonst.

Die Ausgabesequenz wird aus dem Register erhalten $$$0$. Das heißt, die Ausgabesequenz ist $$$\ mathop {\ left \ {{\ mathop S \ nolimits_0 ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

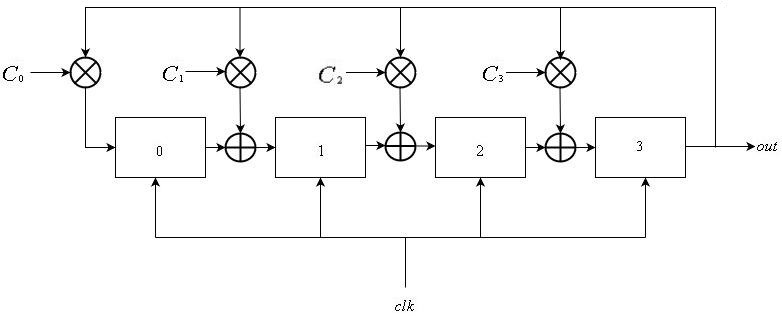
Galois LFSRs

Galois LFSRs bestehen auch aus einer linearen Liste von $$$L$Register aufgezählt von $$$0$zu $$$L-1$, alle teilen sich das globale Taktsignal. Die Eingabe des Registers $$$i$ist die Ausgabe des Registers $$$i-1$für $$$1 \ le i \ le L-1$. Für einige Teilmengen von Registern wird ihre Eingabe mit der Ausgabe des Registers verknüpft $$$L-1$. Dies kann ausgedrückt werden als:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i-1} ^ {t-1} \ oplus \ mathop S \ nolimits_ {L-1} ^ {t-1} \ otimes \ mathop C \ nolimits_i {\ rm {\ \ \ \ if \ \}} 1 \ le i \ le L-1 \\ \ mathop S \ nolimits_ {L-1} ^ {t- 1} \ otimes \ mathop C \ nolimits_0 {\ rm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \}} i = 0 \ end {array} \ right.$$

wo $$$C_i = 1$wenn die Eingabe des Registers $$$i$wird mit der Ausgabe des Registers xored $$$L-1$.


In ähnlicher Weise wie bei Fibonacci-LFSRs wird die Ausgabesequenz definiert als $$$\ mathop {\ left \ {{\ mathop S \ nolimits_ {L-1} ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

Vergleich zwischen Fibonacci und Galois Designs

Es gibt eine direkte Entsprechung zwischen Fibonacci und Galois LFSRs im mathematischen Sinne, wie wir im nächsten Abschnitt sehen werden. Die Verwendung des Designs von Galois bietet jedoch zwei bemerkenswerte Vorteile:

• Bei der Software-Implementierung ist keine erforderlich $$$L$Bitparitätsprüfung, die einen logarithmischen Komplexitätsfaktor hinzufügt.
• Bei der Hardware-Implementierung sind nur Xor-Gatter mit zwei Eingängen erforderlich, deren Ausbreitungsverzögerung erheblich geringer ist als die der Xor-Gatter mit mehreren Eingängen, die in Fibonaccis Design verwendet werden.

In unserem Projekt betrachten wir die Matrixformulierung des LFSR, sodass beide Architekturen austauschbar sind.

Mathematisches Modell von LFSRs

In den folgenden Abschnitten wird, sofern nicht anders angegeben, davon ausgegangen, dass alle Berechnungen im Galois-Feld durchgeführt werden $$$Gf \ left (2 \ right)$. Das heißt, alle Operationen werden modulo berechnet $$$2$. Eine andere Implementierung dieser Konvention ist, dass jede Multiplikation ein logisches und ein Gate ist und jede Summation ein xor-Gate ist.


Betrachten Sie die Zustände aller $$$L$Register eines LFSR zu einem bestimmten Zeitpunkt $$$t$;; Dies kann als Vektor aus dargestellt werden $$${\ left \ {{0,1} \ right \} ^ L}$ ::

$$

$${S ^ t} = \ left ({\ mathop S \ nolimits_0 ^ t; \ mathop S \ nolimits_1 ^ t; \ ldots; \ mathop S \ nolimits_ {L-1} ^ t} \ right)$$

Wir bezeichnen diesen Vektor als den Zustand des LFSR. Beachten Sie, dass es höchstens gibt $$${2 ^ L}$mögliche Zustände für eine $$$L$Register LFSR. Beachten Sie auch, dass ein LFSR, wenn er den Null-Zustand erreicht, keinen anderen Zustand erreichen kann. Deshalb sagen wir, dass es gibt $$$2 ^ L-1$nicht trivial eines LFSR.


Betrachten Sie die folgende lineare Transformation:

$$

$$F = \ left ({\ begin {array} {* {20} {c}} 0 & 1 & \ cdots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & 1 \\ {\ mathop C. \ nolimits_0} & {\ mathop C \ nolimits_1} & \ cdots & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

Angesichts dessen $$$\ mathop S \ nolimits ^ t$Ist der Zustand eines Fibonacci LFSR, kann beobachtet werden, dass

$$

$$F \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Wenn $$$\ mathop S \ nolimits ^ t$war ein Zustand eines Galois LFSR, dann betrachten Transformation $$$G$::

$$

$$G = \ left ({\ begin {array} {* {20} {c}} 0 & \ cdots & 0 & {\ mathop C \ nolimits_0} \\ 1 & \ cdots & 0 & {\ mathop C \ nolimits_1} \\ \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & \ cdots & 1 & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

In diesem Fall haben wir

$$

$$G \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Matrixdarstellungen von LFSRs können bei wiederholten Aktualisierungen flexibel sein, da sie als einfaches Matrixprodukt interpretiert werden können. Es kann beobachtet werden, dass $$$F = {G ^ T}$. Diese Tatsache zeigt die vielen Ähnlichkeiten zwischen Fibonacci und Galois Designs, wenn sie als lineare Transformationen von angesehen wurden $$${\ left \ {{0,1} \ right \} ^ N}$ zu $$${\ left \ {{0,1} \ right \} ^ N}$ .


Das Multiplizieren des Zustandsvektors einiger LFSR mit einer Matrix (vom Fiboancci-Typ oder vom Galois-Typ) wird als Taktung oder Aktualisierung des LFSR bezeichnet.

Der Schaltgenerator

Der Schaltgenerator ist ein taktgesteuerter Generator, der 2015 vorgeschlagen wurde. Er ist nachweislich resistent gegen algebraische und Seitenkanalangriffe. In diesem Abschnitt werden wir das Design des Schaltgenerators vorstellen, wie es von seinen Erfindern angegeben wurde.

Grundstruktur

Der Schaltgenerator besteht aus zwei LFSRs: einem Steuer-LFSR $$$A$von Länge $$$N$und ein Daten-LFSR $$$B$von Länge $$$M$. Control LFSR wird wie zuvor beschrieben aktualisiert. Das Daten-LFSR wird jedoch unter Verwendung einer von zwei möglichen Matrizen aktualisiert. $$$\ mathop M \ nolimits_1 ^ i$oder $$$\ mathop M \ nolimits_2 ^ j$, wo $$${M_1}, {M_2}$sind Begleitmatrizen einiger primitiver Polynome. Die Auswahl einer Matrix gegenüber der anderen wird durch das vom Steuer-LFSR ausgegebene Signal bestimmt. Dieser Prozess kann wie folgt beschrieben werden:

$$

$$\ mathop B \ nolimits ^ t = \ left \ {\ begin {array} {l} \ mathop M \ nolimits_1 ^ i \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 0 \\ \ mathop M \ nolimits_2 ^ j \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 1 \ end {array} \ right.$$

Der Ausgang des Schaltgenerators ist der Ausgang des LFSR $$$B$. Beachten Sie, dass wir das angenommen haben $$$A$ist ein Galois LFSR. Es kann genauso gut ein Fibonacci LFSR sein.


Ganzzahlen $$$i, j$Werden die Schaltindizes genannt.

Der Same

Denken Sie daran, dass ein LFSR höchstens durchlaufen kann $$${2 ^ L} -1$nicht triviale Zustände vor dem erneuten Besuch früherer Zustände. Da Matrizen $$${M_1}, {M_2}$Sind Transformationsmatrizen von LFSRs, können wir diese ganzen Zahlen ableiten $$$i, j$kann höchstens sein $$$2 ^ M-1$bevor sich die Matrizen zu wiederholen beginnen.


Der Keim für den Schaltgenerator ist $$$N + 3M$Bits, die die Anfangszustände der LFSRs darstellen $$$A$und $$$B$und die ganzzahligen Potenzen $$$i, j$. Beachten Sie, dass Matrizen $$${M_1}, {M_2}$sind während der gesamten Implementierung festgelegt und nicht im Seed enthalten.

Verilog Design

In diesem Abschnitt stellen wir unser Design des Schaltgenerators mit Verilog HDL vor. Wir werden jedes Moduldesign von unten nach oben präsentieren. Ganz am Ende stellen wir das Schaltgeneratormodul vor.


Bei unserem Design haben wir versucht, synchrone Komponenten auf ein Minimum zu beschränken. Die einzigen taktgesteuerten Komponenten sind die LFSRs $$$A, B$.


Matrix- und Vektoroperationen können in einer Reihe verschiedener Verfahren implementiert werden, die sich im Verbrauch von Logikeinheiten, Speichereinheiten und der prozeduralen Komplexität unterscheiden. In unserem Design machen wir prozedurale Blöcke überflüssig und verwenden maximal logische Elemente.


Alle Matrizen in den folgenden Modulen werden ab beginnend indiziert $$$0$von links nach rechts und dann von oben nach unten.


Beachten Sie auch, dass alle Module parametrisierte Größen haben. Dies dient zu Debugging-Zwecken. In einer tatsächlichen Implementierung sind alle Größen festgelegt.

Multiplexer

Dies ist ein Modul, das eine 2 zu 1 implementiert $$$N$-bit Multiplexer. Das Modul hat zwei $$$N$-bit-Eingangsleitungen, eine 1-Bit-Auswahlleitung und $$$N$-bit Ausgangsleitung. Wenn der Auswahleingang ist $$$0$dann wird der Ausgang auf die erste Eingabezeile gesetzt, andernfalls wird er auf die zweite gesetzt.


Multiplexer-Modul

Vektortransformation

Dieses Modul implementiert eine lineare Transformation auf einem Vektor. Es akzeptiert als Eingabe ein $$$N \ mal N$Transformationsmatrix und ein $$$N$-bit Vektor. Es gibt das Matrixvektorprodukt seiner Eingabe aus.


Jedes Bit im Ausgabevektor ist das Ergebnis von a $$$N$-bit xor gate, wobei das Ergebnis des $$$N$-bit bitweise und des Eingabevektors und der entsprechenden Matrixzeile. Das heißt, jedes Ausgangsbit ist fest mit dem Eingang verbunden, und es werden keine prozeduralen Blöcke benötigt.


Genau $$$N ^ 2$Zwei-Eingang und Gates werden zusammen mit verwendet $$$N$$$$N$-input xor Gates.


Vektortransformationsmodul

Identität

Dieses Modul akzeptiert keine Eingabe. Es ist $$$N \ mal N$-bit Ausgabe wird auf die initialisiert $$$N$Identitätsmatrix. Ein solches Modul wird der Einfachheit halber deklariert, damit wir nicht für jede unterschiedliche Größe einen globalen Registervektor initialisieren müssen.


Identitätsmatrix-Modul

Transponieren

Dieses Modul akzeptiert eine $$$N \ mal N$Matrix und Ausgabe seiner Transponierten. In diesem Modul werden weder logische noch Speicherelemente verwendet, seine Ausgabe ist lediglich eine Permutation seiner Eingabe
.

Matrix-Transponierungsmodul

Matrixmultiplikation

Dies ist ein Modul, das die Matrix-Matrix-Multiplikation implementiert. Es akzeptiert zwei $$$N \ mal N$Matrizen als Eingabe und Ausgabe ihres Matrix-Matrix-Produkts.


Dieses Modul enthält eine Instanz des Matrixtransponierungsmoduls. Dies ermöglicht es, Spalten in der zweiten Eingabematrix aufeinanderfolgende Indizes zuzuweisen. Jeder Eintrag in der Ausgabematrix wird dann der Ausgabe von a zugeordnet $$$N$-Eingabe xoder Gatter, dessen Eingabe die bitweise und der entsprechenden Zeile aus der ersten Matrix und Spalte aus der zweiten ist.


Genau $$$N ^ 3$Zwei-Eingang und Tore und $$$N ^ 2$$$$N$-input xor werden in dieser Implementierung verwendet.


Matrix-Multiplikationsmodul

Matrixexponentiation

Dieses Modul erhöht eine Matrix auf eine ganzzahlige Potenz. Es akzeptiert als Eingabe ein $$$N \ mal N$Matrix und a $$$K$-bit Ganzzahl. Seine Ausgabe ist die Matrix, die auf die angegebene ganzzahlige Potenz angehoben wird.


Matrix-Exponentiationsmodul

Steuereinheit

Dieses Modul implementiert die $$$N$-bit control LFSR. Es ist eines der beiden taktgesteuerten Module in unserem Design.


Es enthält eine statische $$$N \ mal N$LFSR-Transformationsmatrix und eine Variable $$$N$-bit Zustand. Sein Eingang enthält eine Uhr, eine $$$N$-bit state reset und ein Reset-Signal. Seine Ausgabe ist ein einzelnes Bit, das das letzte Bit des LFSR ist.


Nach jeder positiven Flanke des Taktsignals wird der Zustand gemäß der Transformationsmatrix unter Verwendung eines Matrixvektormultiplikationsmoduls aktualisiert. Das Zurücksetzen des Zustands wird nach jeder positiven Flanke des Rücksetzsignals dem internen Zustand zugewiesen.





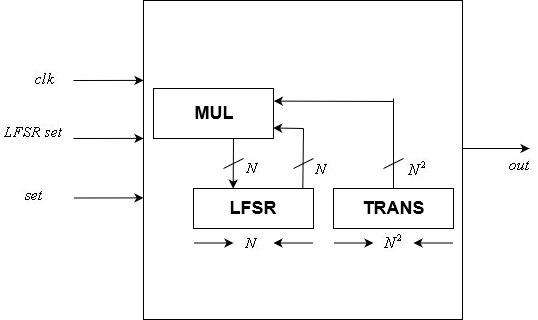Steuergerätemodul

Dateneinheit

Die $$$N$Daten LFSR wird mit diesem Modul implementiert. Wie das Steuergerätemodul ist es taktgesteuert


Das Modul enthält zwei $$$N \ mal N$Transformationsmatrizen und eine $$$N$-bit LFSR-Status. Es akzeptiert als Eingang ein Taktsignal, ein Steuersignal, ein $$$N$-bit LFSR-Status zurückgesetzt, zwei $$$N \ mal N$Matrixtransformation wird zurückgesetzt und ein Rücksetzsignal. Es hat eine Ein-Bit-Ausgabe, das letzte Bit des internen LFSR.


Da der Startwert geändert werden kann, können auch die Transformationsmatrizen geändert werden, im Gegensatz zu der Steuereinheit, deren Transformationsmatrix fest ist.




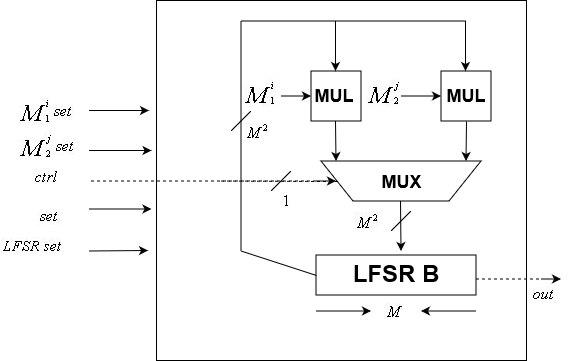\ Dateneinheit

Der Schaltgenerator

Dies ist das Hauptmodul unseres Designs. Es wird durch ganze Zahlen parametrisiert $$$N, M$Dies sind die Größen der Steuer- bzw. Dateneinheiten.


Der Eingang zu diesem Modul ist ein Taktsignal, a $$$N + 3M$-bit Seed und ein gesetztes Signal. Der Startwert ist einfach eine Verkettung des Steuer-LFSR-Resets, des Daten-LFSR-Resets und der Ganzzahlen $$$i, j$Sein Ausgang ist ein Bit, das vom Schaltgenerator erzeugte Pseudozufallsbit.


Dieses Modul enthält zwei $$$M \ mal M$Matrizen $$$\ mathop M \ nolimits_1, \ mathop M \ nolimits_2$. Diese Matrizen sind während der gesamten Implementierung festgelegt.


Zwei Instanzen von Matrixexponentiationsmodulen werden verwendet, um die Eingabematrizen für die Dateneinheit zu berechnen, wobei ihre Eingabe die festen Transformationsmatrizen und ganzen Zahlen sind $$$i, j$, aus dem Samen extrahiert.


Das Schaltgeneratormodul

Schlussfolgerungen und Empfehlungen

In diesem Projekt haben wir ein Design des Schaltgenerators mit Verilog HDL vorgestellt. Dieses Design konzentriert sich ausschließlich auf Hardware und macht die Verwendung von Verfahrensblöcken überflüssig. Ein solcher Ansatz ermöglicht maximale Leistung auf Kosten von Logik- und Speicherelementen. Bei einigen Anwendungen mit Einschränkungen in Bezug auf Logik und Speicherelemente kann es vorteilhaft sein, die Leistung zu beeinträchtigen und die Verwendung von Prozedurblöcken zu erhöhen, um die Verwendung elektronischer Elemente zu reduzieren.


Ein Nachteil des Projekts ist, dass es die Verantwortung für die Auswahl guter Schaltindizes beim Benutzer trägt. Ein möglicher Fortschritt ist das Hinzufügen einer Hardwarekomponente, um die Gültigkeit des verwendeten Schaltindex zu überprüfen. Dies erfordert eine Hardware-Implementierung komplexer Algorithmen, z. B. das Auffinden des Charakteristikpolynoms einer bestimmten Matrix und das Überprüfen auf Primitivität.


Ein möglicher Fortschritt besteht darin, einen echten Zufallszahlengenerator hinzuzufügen, um zufällige Schaltindizes zu überprüfen, und ein gültiges Paar auszugeben, sobald es gefunden wurde. Es kann nachgewiesen werden, dass dieser Prozess mit kurzer Wahrscheinlichkeit nach kurzer Zeit anhält.

Referenzen

1. Katz, Jonathan et al. Handbuch der angewandten Kryptographie. CRC Press, 1996.
2. Choi, Jun et al. "Der Schaltgenerator: Neuer taktgesteuerter Generator mit Widerstand gegen algebraische und Seitenkanalangriffe." Entropy 17.6 (2015): 3692 & ndash; 3709.
3. Shamir, Adi. "Stream-Chiffren: tot oder lebendig?" ASIACRYPT. 2004.
4. LFSRs für Uneingeweihte