Ein bisschen Theorie, die ich über Sound kenne - Sound ist:
eine Welle, Schwingungen, gedämpfte Schwingungen, eine Welle kann physikalisch beschrieben werden, eine Welle kann mathematisch beschrieben werden.
Laden Sie das Programm herunter und testen Sie es
Da wir auf einem Computer modellieren, wird unsere Welle unter Verwendung einer Folge (Fourier-Reihe) von Bytes (Zahlen von -128 bis 127 und Null) beschrieben, dh einer Anordnung von Bytes.
Die Schwingungsgleichung wird am besten durch die SIN-Funktion beschrieben.
Stimmen Sie zu, es wäre zu einfach, wenn wir nur die SIN-Funktion über das Array ausführen würden.
Aus diesem Grund habe ich anhand von Artikeln zur Beschreibung des Yamaha-Synthesizer-Geräts den folgenden Algorithmus geschrieben:
1. Mit der SIN-Funktion wird eine Haupt- oder Modellierungswelle erstellt. Hier ist eine Formel, die für andere Entwickler nützlich sein kann:
for(int k = 0; k < SoundLabVisual.player.data.length;k++){ double sinusoid = amplitude1 * Math.sin(2 * (3.14/1 ) * k * frequency1 + faza); }
Wo:
Amplitude1 - Amplitude
Frequenz1 - Schwingungsfrequenz
Faza - die Anfangsphase der Schwingungen
2. Mit der zweiten SIN-Funktion wird eine Hauptwelle erzeugt, deren Amplitude der Wert der ersten Welle ist:
Screenshot programmieren
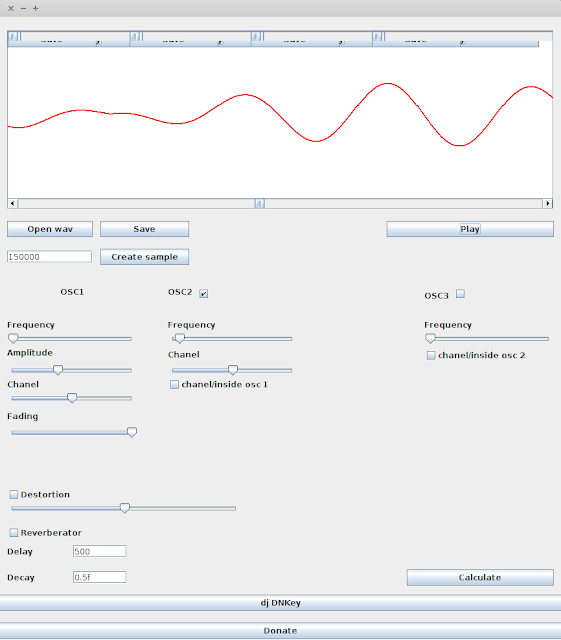
Ich habe die Test-Sounds in das lmms-Programm geladen.
 Hören Sie mp3
Hören Sie mp3Ein weiterer Algorithmus wird implementiert, der auf den Kanälen funktioniert. Wenn möglich, werde ich im zweiten Artikel darüber schreiben.
Update:
Nach den Kommentaren von Kommentatoren können Algorithmen nun für sich und untereinander multipliziert werden.
if(jCheckBox8.isSelected()){ sinusoid = (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))) * (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))); }else{ sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 )); }
Update 2: Das Programm wurde aktualisiert, jetzt kann die Welle mit dem Sound gemischt werden.