Der Artikel befasst sich mit der Analyse und Untersuchung von Materialien des Wettbewerbs für die Suche nach Schiffen auf See.

Versuchen wir zu verstehen, wie und wonach das Netzwerk sucht und was es findet. Dieser Artikel ist einfach das Ergebnis von Neugier und müßigem Interesse, nichts davon ist in der Praxis zu finden und für praktische Aufgaben gibt es nichts zum Kopieren und Einfügen. Das Ergebnis wird jedoch nicht vollständig erwartet. Das Internet ist voll von Beschreibungen des Betriebs von Netzwerken, in denen die Autoren schön beschreiben und mit Bildern, wie Netzwerke Primitive bestimmen - Winkel, Kreise, Whisker, Schwänze usw. -, dann werden sie nach Segmentierung / Klassifizierung gesucht. Viele Wettbewerbe werden mit Gewichten aus anderen großen und breiten Netzwerken gewonnen. Es ist interessant zu verstehen und zu sehen, wie und welche Grundelemente ein Netzwerk aufbaut.
Wir werden eine kleine Studie durchführen und die Optionen prüfen - die Argumentation und der Code des Autors werden vorgestellt, Sie können alles selbst überprüfen / ergänzen / ändern.
Der Kaggle Marine Search Wettbewerb ist vor kurzem beendet. Airbus schlug vor, Satellitenbilder des Meeres mit und ohne Schiffe zu analysieren. Insgesamt 192555 Bilder 768x768x3 - es sind 340 720 680 960 Bytes, wenn uint8 und viermal so viel, wenn float32 (übrigens float32 ist schneller als float64, weniger Speicherzugriff) und auf 15606 Bildern müssen Sie Schiffe finden. Wie üblich wurden alle wichtigen Plätze von Personen eingenommen, die an ODS (ods.ai) beteiligt sind, was natürlich und zu erwarten ist, und ich hoffe, dass wir bald den Gedankengang und den Kodex der Gewinner und Preisträger studieren können.
Wir werden ein ähnliches Problem betrachten, es aber erheblich vereinfachen - nehmen Sie das Meer np.random.sample () * 0.5, wir brauchen keine Wellen, Wind, Strände und andere versteckte Muster und Gesichter. Lassen Sie uns das Bild des Meeres im RGB-Bereich von 0,0 bis 0,5 wirklich zufällig machen. Wir werden die Gefäße auch in der gleichen Farbe bemalen und sie vom Meer unterscheiden. Wir werden sie in den Bereich von 0,5 bis 1,0 bringen und sie werden alle die gleiche Form haben - Ellipsen unterschiedlicher Größe und Ausrichtung.

Nehmen Sie eine sehr verbreitete Version des Netzwerks (Sie können Ihr Lieblingsnetzwerk verwenden) und wir werden alle Experimente damit durchführen.
Als nächstes werden wir die Parameter des Bildes ändern, Interferenzen erzeugen und Hypothesen erstellen - also werden wir die Hauptmerkmale hervorheben, anhand derer das Netzwerk Ellipsen findet. Vielleicht wird der Leser seine Schlussfolgerungen ziehen und den Autor widerlegen.
Wir laden Bibliotheken, wir bestimmen die Größe eines Arrays von Bildernimport numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm_notebook, tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau from keras.models import load_model from keras.optimizers import Adam from keras.layers import Input, Conv2D, Conv2DTranspose, MaxPooling2D, concatenate, Dropout from keras.losses import binary_crossentropy import tensorflow as tf import keras as keras from keras import backend as K from tqdm import tqdm_notebook w_size = 256 train_num = 8192 train_x = np.zeros((train_num, w_size, w_size,3), dtype='float32') train_y = np.zeros((train_num, w_size, w_size,1), dtype='float32') img_l = np.random.sample((w_size, w_size, 3))*0.5 img_h = np.random.sample((w_size, w_size, 3))*0.5 + 0.5 radius_min = 10 radius_max = 30
Bestimmen Sie die Verlust- und Genauigkeitsfunktionen def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
Wir verwenden die klassische Metrik bei der Bildsegmentierung. Es gibt viele Artikel, Code mit Kommentaren und Text zu der ausgewählten Metrik. Auf derselben Ebene gibt es viele Optionen mit Kommentaren und Erklärungen. Wir werden die Maske des Pixels vorhersagen - dies ist das "Meer" oder "Boot" und die Wahrheit oder Falschheit der Vorhersage bewerten. Das heißt, Die folgenden vier Optionen sind möglich: Wir haben richtig vorausgesagt, dass ein Pixel ein „Meer“ ist, richtig vorausgesagt, dass ein Pixel ein „Schiff“ ist, oder einen Fehler bei der Vorhersage eines „Meeres“ oder eines „Schiffs“ gemacht. Daher schätzen wir für alle Bilder und alle Pixel die Anzahl aller vier Optionen und berechnen das Ergebnis - dies ist das Ergebnis des Netzwerks. Und je weniger fehlerhafte Vorhersagen und wahrer, desto genauer das Ergebnis und desto besser das Netzwerk.
Nehmen wir für die Forschung das gut untersuchte U-Net, ein hervorragendes Netzwerk für die Bildsegmentierung. Das Netzwerk ist in solchen Wettbewerben sehr verbreitet und es gibt viele Beschreibungen, Feinheiten der Anwendung usw. Es wurde eine Variante des klassischen U-Netzes gewählt und es war natürlich möglich, es zu aktualisieren, Restblöcke hinzuzufügen usw. Aber „Sie können die Unermesslichkeit nicht annehmen“ und alle Experimente und Tests gleichzeitig durchführen. U-net führt eine sehr einfache Operation mit Bildern durch - es reduziert die Größe des Bildes mit einigen Transformationen Schritt für Schritt und versucht dann, die Maske aus dem komprimierten Bild wiederherzustellen. Das heißt, Die Dimension des Bildes wird in unserem Fall auf 32 x 32 gebracht, und dann versuchen wir, die Maske mithilfe der Daten aller vorherigen Komprimierungen wiederherzustellen.
Im Bild stammt das U-Net-Schema aus dem Originalartikel, aber wir haben es ein wenig überarbeitet, aber das Wesentliche bleibt gleich - wir komprimieren das Bild → erweitern es zu einer Maske.
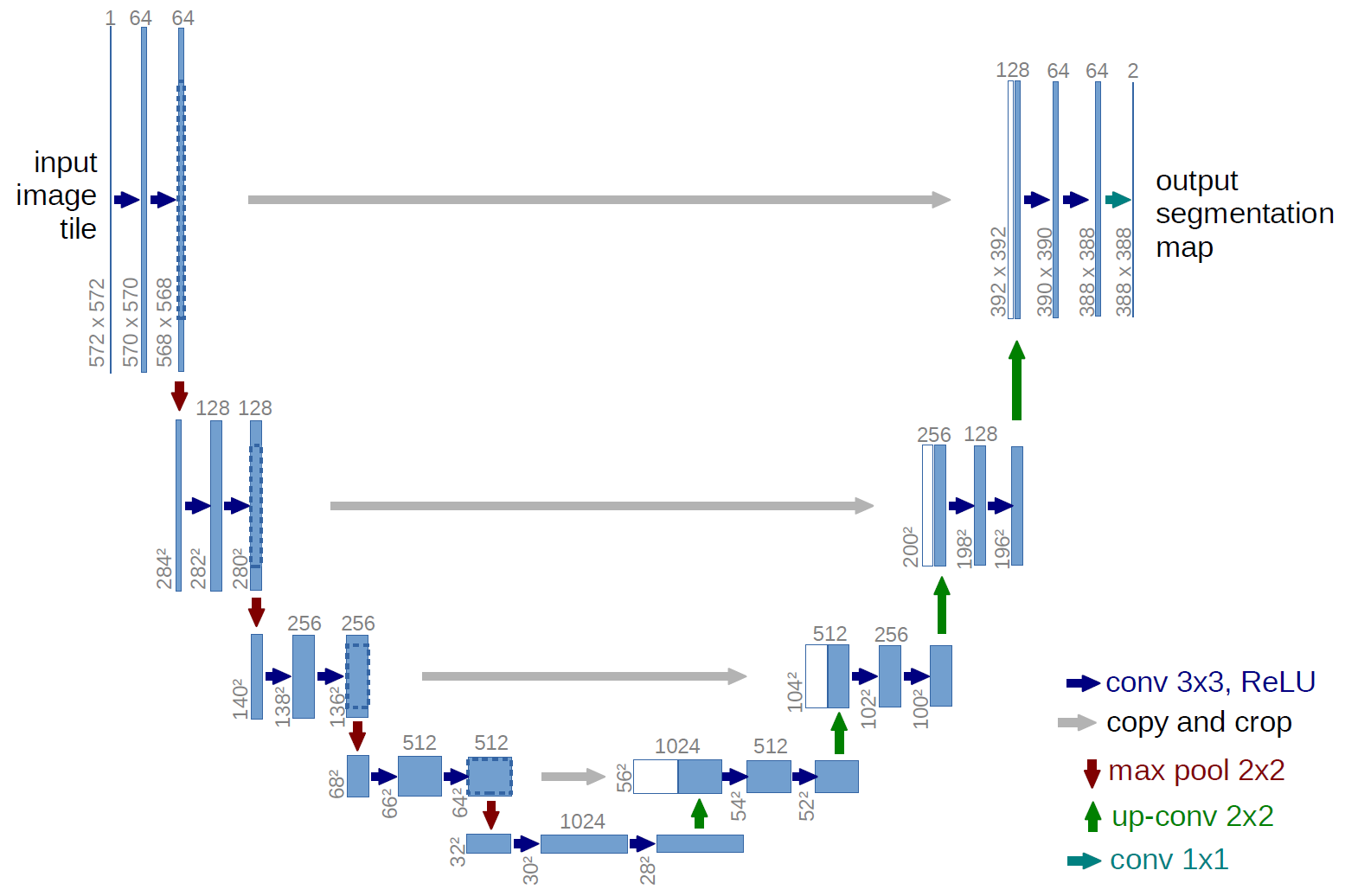
Nur U-net def build_model(input_layer, start_neurons): conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(input_layer) conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(conv1) pool1 = MaxPooling2D((2, 2))(conv1) pool1 = Dropout(0.25)(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(conv2) pool2 = MaxPooling2D((2, 2))(conv2) pool2 = Dropout(0.5)(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(conv3) pool3 = MaxPooling2D((2, 2))(conv3) pool3 = Dropout(0.5)(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(conv4) pool4 = MaxPooling2D((2, 2))(conv4) pool4 = Dropout(0.5)(pool4)
Erstes Experiment. Am einfachsten
Die erste Version unseres Experiments wurde der Einfachheit halber sehr einfach gewählt - das Meer ist heller, Schiffe sind dunkler. Alles ist sehr einfach und offensichtlich. Wir gehen davon aus, dass das Netzwerk Schiffe / Ellipsen ohne Probleme und mit Genauigkeit finden wird. Die Funktion next_pair generiert ein Bild- / Maskenpaar, in dem Ort, Größe und Drehwinkel zufällig ausgewählt werden. Ferner werden alle Änderungen an dieser Funktion vorgenommen - eine Änderung der Farbe, Form, Interferenz usw. Aber jetzt, als einfachste Option, testen wir die Hypothese von dunklen Booten auf hellem Hintergrund.
def next_pair(): p = np.random.sample() - 0.5
Wir erzeugen den ganzen Zug und sehen, was passiert ist. Es sieht aus wie Boote auf See und sonst nichts. Alles ist klar sichtbar, klar und verständlich. Die Position ist zufällig und es gibt nur eine Ellipse in jedem Bild.
for k in range(train_num):
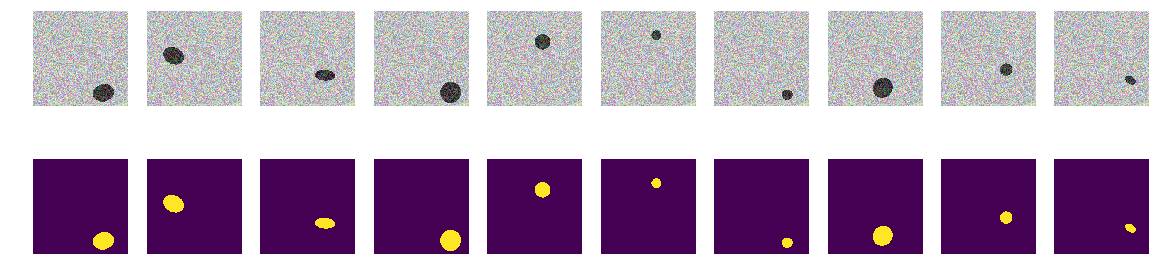
Es besteht kein Zweifel, dass das Netzwerk erfolgreich lernen und Ellipsen finden wird. Testen wir jedoch unsere Hypothese, dass das Netzwerk darauf trainiert ist, Ellipsen / Schiffe zu finden und gleichzeitig mit hoher Genauigkeit.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.save_weights('./keras.weights') while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.2272 - my_iou_metric: 0.7325 - val_loss: 0.0063 - val_my_iou_metric: 1.0000
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0090 - my_iou_metric: 1.0000 - val_loss: 0.0045 - val_my_iou_metric: 1.0000
Das Netzwerk findet erfolgreich Ellipsen. Es ist jedoch keineswegs bewiesen, dass sie nach Ellipsen im Verständnis des Menschen sucht. Als Region, die durch die Ellipsengleichung begrenzt und mit Inhalten gefüllt ist, die sich vom Hintergrund unterscheiden, gibt es keine Gewissheit, dass es Netzwerkgewichte gibt, die den Koeffizienten der quadratischen Ellipsengleichung ähnlich sind. Und es ist offensichtlich, dass die Helligkeit der Ellipse geringer ist als die Helligkeit des Hintergrunds und kein Geheimnis oder Rätsel - wir gehen davon aus, dass wir nur den Code überprüft haben. Lassen Sie uns das offensichtliche Gesicht korrigieren und den Hintergrund und die Farbe der Ellipse ebenfalls zufällig festlegen.
Zweite Option
Jetzt sind die gleichen Ellipsen auf dem gleichen Meer, aber die Farbe des Meeres und dementsprechend das Boot wird zufällig ausgewählt. Wenn das Meer dunkler ist, ist das Schiff heller und umgekehrt. Das heißt, Durch die Helligkeit der Punktgruppe ist es unmöglich zu bestimmen, ob sie sich außerhalb der Ellipse befinden, d. h. des Meeres, oder ob es sich um Punkte innerhalb der Ellipse handelt. Wieder testen wir unsere Hypothese, dass das Netzwerk Ellipsen unabhängig von der Farbe findet.
def next_pair(): p = np.random.sample() - 0.5
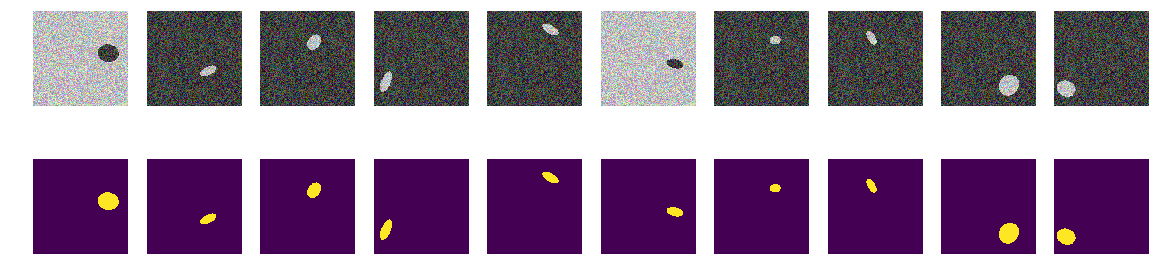
Anhand des Pixels und seiner Umgebung ist es nun unmöglich, den Hintergrund oder die Ellipse zu bestimmen. Wir generieren auch Bilder und Masken und schauen uns die ersten 10 auf dem Bildschirm an.
Masken bauen for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.4652 - my_iou_metric: 0.5071 - val_loss: 0.0439 - val_my_iou_metric: 0.9005
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.1418 - my_iou_metric: 0.8378 - val_loss: 0.0377 - val_my_iou_metric: 0.9206Das Netzwerk kann alle Ellipsen problemlos verarbeiten und finden. Aber hier gibt es einen Fehler in der Implementierung, und alles ist offensichtlich - der kleinere der beiden Bereiche im Bild ist eine Ellipse, ein weiterer Hintergrund. Vielleicht ist dies eine falsche Hypothese, aber korrigieren Sie sie trotzdem. Fügen Sie dem Bild mit der gleichen Farbe wie die Ellipse ein weiteres Polygon hinzu.
Dritte Option
In jedem Bild wählen wir zufällig die Farbe des Meeres aus den beiden Optionen aus und fügen eine Ellipse und ein Rechteck hinzu, die sich beide von der Farbe des Meeres unterscheiden. Es stellt sich das gleiche "Meer" heraus, auch ein gemaltes "Boot", aber im gleichen Bild fügen wir ein Rechteck der gleichen Farbe wie das "Boot" und auch mit einer zufällig ausgewählten Größe hinzu. Jetzt ist unsere Annahme komplizierter, auf dem Bild gibt es zwei identisch gefärbte Objekte, aber wir nehmen an, dass das Netzwerk immer noch lernen wird, das richtige Objekt auszuwählen.
Programm zum Zeichnen von Ellipsen und Rechtecken Nach wie vor berechnen wir Bilder und Masken und schauen uns die ersten 10 Paare an.
Gebäudemaskenbilder Ellipsen und Rechtecke for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 57s 8ms/step - loss: 0.7557 - my_iou_metric: 0.0937 - val_loss: 0.2510 - val_my_iou_metric: 0.4580
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.0719 - my_iou_metric: 0.8507 - val_loss: 0.0183 - val_my_iou_metric: 0.9812Es war nicht möglich, die Rechtecke des Netzwerks zu verwechseln, und unsere Hypothese wird bestätigt. Nach Beispielen und Diskussionen zu urteilen, hatten alle Teilnehmer des Airbus-Wettbewerbs einzelne Schiffe, und mehrere Schiffe befanden sich ziemlich genau in der Nähe. Die Ellipse aus dem Rechteck - d.h. Das Schiff ist vom Haus am Ufer, das Netzwerk wird unterschieden, obwohl die Polygone die gleiche Farbe wie die Ellipsen haben. Es ist keine Frage der Farbe, denn sowohl die Ellipse als auch das Rechteck werden gleichermaßen zufällig gemalt.
Vierte Option
Vielleicht unterscheidet sich das Netzwerk durch Rechtecke - richtig, verzerren Sie sie. Das heißt, Das Netzwerk findet leicht beide geschlossenen Bereiche unabhängig von ihrer Form und verwirft den Rechteckbereich. Dies ist die Hypothese des Autors - wir werden sie überprüfen, für die wir keine Rechtecke, sondern viereckige Polygone beliebiger Form hinzufügen. Unsere Hypothese ist wiederum, dass das Netzwerk eine Ellipse von einem beliebigen viereckigen Polygon derselben Farbe unterscheidet.
Sie können natürlich in das Innere des Netzwerks eindringen und dort die Ebenen betrachten und die Bedeutung von Gewichten und Verschiebungen analysieren. Der Autor interessiert sich für das resultierende Verhalten des Netzwerks, das Urteil basiert auf dem Ergebnis der Arbeit, obwohl es immer interessant ist, nach innen zu schauen.
Nehmen Sie Änderungen an der Bilderzeugung vor def next_pair(): p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min) p1 = np.rint(np.random.sample()*(w_size-radius_max)) p2 = np.rint(np.random.sample()*(w_size-radius_max)) p3 = np.rint(np.random.sample()*2.*radius_min - radius_min) p4 = np.rint(np.random.sample()*2.*radius_min - radius_min) p5 = np.rint(np.random.sample()*2.*radius_min - radius_min) p6 = np.rint(np.random.sample()*2.*radius_min - radius_min) p7 = np.rint(np.random.sample()*2.*radius_min - radius_min) p8 = np.rint(np.random.sample()*2.*radius_min - radius_min) poly = np.array(( (p1, p2), (p1+p3, p2+p4+p0), (p1+p5+p0, p2+p6+p0), (p1+p7+p0, p2+p8), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc = list(set(rr) & set(rr_p)) if len(in_sc) > 0: if np.mean(rr_p) > np.mean(in_sc): poly += np.max(in_sc) - np.min(in_sc) else: poly -= np.max(in_sc) - np.min(in_sc) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img = img_l.copy() img[rr, cc] = img_h[rr, cc] img[rr_p, cc_p] = img_h[rr_p, cc_p] else: img = img_h.copy() img[rr, cc] = img_l[rr, cc] img[rr_p, cc_p] = img_l[rr_p, cc_p] msk = np.zeros((w_size, w_size, 1), dtype='float32') msk[rr, cc] = 1. return img, msk
Wir berechnen Bilder und Masken und schauen uns die ersten 10 Paare an.
Wir bauen Bilder, Masken, Ellipsen und Polygone for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

Wir starten unser Netzwerk. Ich möchte Sie daran erinnern, dass dies für alle Optionen gleich ist.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.6815 - my_iou_metric: 0.2168 - val_loss: 0.2078 - val_my_iou_metric: 0.4983
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.1470 - my_iou_metric: 0.6396 - val_loss: 0.1046 - val_my_iou_metric: 0.7784
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0642 - my_iou_metric: 0.8586 - val_loss: 0.0403 - val_my_iou_metric: 0.9354
Die Hypothese wird bestätigt, Polygone und Ellipsen sind leicht zu unterscheiden. Ein aufmerksamer Leser wird hier bemerken - natürlich sind sie anders, eine Unsinnsfrage, jede normale KI kann eine Kurve zweiter Ordnung von der Linie der ersten unterscheiden. Das heißt, Das Netzwerk bestimmt leicht das Vorhandensein einer Grenze in Form einer Kurve zweiter Ordnung. Wir werden nicht streiten, das Oval durch ein Siebeneck ersetzen und prüfen.
Fünftes Experiment, das schwierigste
Es gibt keine Kurven, nur glatte Flächen mit regelmäßig geneigten und gedrehten Heptagonen und beliebige viereckige Polygone. Wir führen in die Funktion den Bild- / Maskengenerator ein - nur Projektionen von regulären Heptagonen und beliebigen viereckigen Polygonen derselben Farbe.
endgültige Überarbeitung der Bilderzeugungsfunktion def next_pair(_n = 7): p = np.random.sample() - 0.5 c_x = np.random.sample()*(w_size-2*radius_max) + radius_max c_y = np.random.sample()*(w_size-2*radius_max) + radius_max radius = np.random.sample()*(radius_max-radius_min) + radius_min d = np.random.sample()*0.5 + 1 a_deg = np.random.sample()*360 a_rad = np.deg2rad(a_deg) poly = []
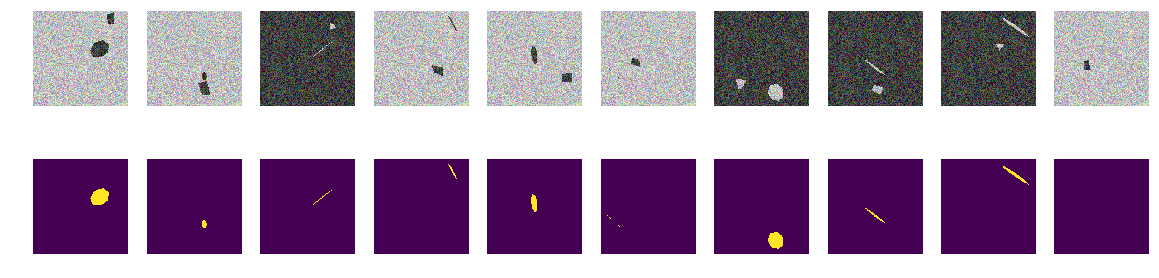
Nach wie vor bauen wir Arrays und schauen uns die ersten 10 an.
Masken bauen for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 54s 7ms/step - loss: 0.5005 - my_iou_metric: 0.1296 - val_loss: 0.1692 - val_my_iou_metric: 0.3722
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.1287 - my_iou_metric: 0.4522 - val_loss: 0.0449 - val_my_iou_metric: 0.6833
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0759 - my_iou_metric: 0.5985 - val_loss: 0.0397 - val_my_iou_metric: 0.7215
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0455 - my_iou_metric: 0.6936 - val_loss: 0.0297 - val_my_iou_metric: 0.7304
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0432 - my_iou_metric: 0.7053 - val_loss: 0.0215 - val_my_iou_metric: 0.7846
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0327 - my_iou_metric: 0.7417 - val_loss: 0.0171 - val_my_iou_metric: 0.7970
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0265 - my_iou_metric: 0.7679 - val_loss: 0.0138 - val_my_iou_metric: 0.8280Zusammenfassung
Wie Sie sehen können, unterscheidet das Netzwerk zwischen Projektionen von regulären Heptagonen und beliebigen viereckigen Polygonen mit einer Genauigkeit von 0,828 auf dem Testsatz. Das Netzwerktraining wird durch einen beliebigen Wert von 0,75 gestoppt, und die Genauigkeit sollte höchstwahrscheinlich viel besser sein. Wenn wir von der These ausgehen, dass das Netzwerk Primitive findet und deren Kombinationen das Objekt bestimmen, dann gibt es in unserem Fall zwei Bereiche mit einem anderen Durchschnitt als dem Hintergrund, es gibt keine Primitiven im Verständnis des Menschen. Es gibt keine offensichtlichen einfarbigen Linien und keine Ecken, nur Bereiche mit sehr ähnlichen Rändern. Selbst wenn Sie Linien erstellen, werden beide Objekte im Bild aus denselben Grundelementen erstellt.
Eine Frage für Kenner - Was betrachtet das Netzwerk als Zeichen, anhand dessen es „Boote“ von „Störungen“ unterscheidet? Offensichtlich ist dies nicht die Farbe oder Form der Ränder der Boote. Natürlich können wir diese abstrakte Konstruktion der "See" / "Schiffe" weiter untersuchen, wir sind nicht die Akademie der Wissenschaften und können ausschließlich aus Neugier forschen. Wir können die Heptagone in Achtecke ändern oder das Bild mit regulären fünf und sechs Winkeln füllen und sehen, ob sich ihr Netzwerk unterscheidet oder nicht. Ich überlasse dies den Lesern - obwohl ich mich auch gefragt habe, ob das Netzwerk die Anzahl der Ecken des Polygons zählen und für den Test nicht reguläre Polygone im Bild anordnen kann, sondern deren zufällige Projektionen.
Es gibt andere, nicht weniger interessante Eigenschaften solcher Boote, und solche Experimente sind nützlich, da wir selbst alle probabilistischen Eigenschaften des untersuchten Satzes festlegen und das unerwartete Verhalten gut untersuchter Netzwerke Wissen hinzufügen und Vorteile bringen wird.
Hintergrund zufällig ausgewählt, Farbe zufällig ausgewählt, Boots- / Ellipsenposition zufällig ausgewählt. Es gibt keine Linien in den Bildern, es gibt Bereiche mit unterschiedlichen Eigenschaften, aber es gibt keine einfarbigen Linien! In diesem Fall gibt es natürlich Vereinfachungen und die Aufgabe kann noch komplizierter sein - wählen Sie beispielsweise Farben wie 0,0 ... 0,9 und 0,1 ... 1,0 -, aber für das Netzwerk gibt es keinen Unterschied. Das Netzwerk kann und findet Muster, die sich von denen unterscheiden, die eine Person klar sieht und findet.
Wenn einer der Leser interessiert ist, können Sie weiter in den Netzwerken recherchieren und auswählen, wenn dies nicht funktioniert oder nicht klar ist oder plötzlich ein neuer und guter Gedanke auftaucht und mit seiner Schönheit beeindruckt, können Sie ihn jederzeit mit uns teilen oder die Meister (und auch die Großmeister) fragen. und bitten Sie um qualifizierte Hilfe in der ODS-Community.