Die neuen Beweise, die vom australischen Science-Fiction-Autor Greg Egan verfasst wurden, und der anonym online veröffentlichte Beweis von 2011 wurden als bedeutende Durchbrüche bei der Untersuchung des Geheimnisses anerkannt, das Mathematiker seit 25 Jahren erforschen.

Am 16. September 2011 veröffentlichte ein Anime-Fan im Forum eine 4-Kanal-Mathematikfrage zur Kult-Serie „Die
Melancholie von Haruhi Suzumiya “. Die erste Staffel der Show, in der es Zeitreisen gab, wurde in einer anderen Reihenfolge als die chronologische gezeigt, und während der anschließenden Show und Veröffentlichung auf DVD wurde die Reihenfolge der Episoden erneut geändert. Im Internet diskutierten die Fans in welcher Reihenfolge es besser ist, die Serie zu sehen, und der Autor der Frage fragte: Wenn das Publikum die Serie in allen möglichen Reihenfolgen sehen wollte, wie viele Folgen wären auf ihrer kürzesten Liste? [
bezieht sich auf eine Liste, in der Sie eine beliebige Folge von Folgen finden können / ca. perev. ]]
In weniger als einer Stunde gab ein anonymer Autor eine
Antwort auf die Frage - keine vollständige Lösung, sondern eine Untergrenze für die erforderliche Anzahl von Episoden. Aus seiner Überlegung, die auf eine beliebige Anzahl von Episoden anwendbar ist, folgte, dass die Zuschauer für die erste Staffel von Haruhi, die aus 14 Episoden besteht, mindestens 93.884.313.611 Episoden hintereinander sehen müssten, um alle möglichen Permutationen zu untersuchen. "Untersuchen Sie die Beweise auf Fehler, die ich möglicherweise übersehen habe", schrieb der Autor der Antwort.
Sieben Jahre lang blieb der Beweis in der mathematischen Gemeinschaft unbemerkt - es stellte sich heraus, dass ihn in diesem Moment nur ein professioneller Mathematiker bemerkte und er ihn nicht gründlich genug studierte. Der australische Science-Fiction-Autor
Greg Egan hat jedoch im vergangenen Monat plötzlich eine neue
Obergrenze für die Anzahl der benötigten Folgen festgelegt. Die Entdeckung von Egan weckte erneut das Interesse an der Aufgabe und machte auf die Aufzeichnung über die Untergrenze von 2011 aufmerksam. Beide Beweise gelten heute als bedeutende Durchbrüche bei der Erforschung des Rätsels, das Mathematiker seit mindestens 25 Jahren erforschen.
Mathematiker überprüften schnell die Obergrenze von Egan, die wie die Untergrenze auf Sequenzen beliebiger Länge anwendbar ist. Dann bestätigten Robin Houston, Mathematiker bei Kiln, einem Unternehmen für Datenvisualisierung, und
Jay Panton von der Marquette University in Milwaukee unabhängig voneinander die Arbeit eines anonymen Autors mit 4chan. "Es wurden große Anstrengungen unternommen, um die Gültigkeit dieser Hypothese zu überprüfen", sagte Panton, da die Schlüsselideen des Beweises nicht klar genug ausgedrückt wurden.
Und jetzt haben Houston und Panton zusammen mit
Vince Vater von der University of Florida eine
formelle Arbeit geschrieben . Darin gaben sie den Erstautor als „anonymes 4-Kanal-Poster“ an.
"Das Seltsame ist, dass dieser sehr elegante Beweis einer zuvor unbekannten Tatsache an einem so unwahrscheinlichen Ort erschien", sagte Houston.
Städte mit Permutationen
Wenn die Serie nur drei Folgen enthält, gibt es sechs Möglichkeiten, sie anzusehen: 123, 132, 213, 231, 312 und 321. Sie können zusammengeklebt werden und eine Liste mit 18 Folgen erstellen, einschließlich jeder Version der Bestellung. Es gibt jedoch auch eine effizientere Klebemethode: 123121321. Eine solche Sequenz, die alle Permutationen eines Satzes von n Zeichen enthält, wird als Superpermutation bezeichnet.
Im Jahr 1993 entdeckten Daniel Ashlock und Janet Tilotson, dass beim Studium der kürzesten Superpermutationen für verschiedene Werte von n schnell Fakultäten auftreten - dieselben Werte, die in der Form n! Geschrieben sind, d. H. Alle Zahlen von 1 bis n multiplizieren (zum Beispiel 4) ! = 4 * 3 * 2 * 1).
Wenn Ihre Serie nur 1 Episode enthält, beträgt die Länge der kürzesten Superpermutation 1! (auch als die gute alte Einheit bekannt). Für eine Serie von zwei Episoden hat die kürzeste Superpermutation (121) eine Länge von 2! + 1! .. Für drei Folgen (Beispiel oben) beträgt die Länge 3! + 2! + 1! Und für vier Folgen (123412314231243121342132413214321) ist es 4! + 3! + 2! + 1! .. Die Fakultätsregel wurde allgemein akzeptiert (obwohl niemand beweisen konnte, dass sie für alle n gilt), und spätere Mathematiker bestätigten sie für n = 5.
Dann beeindruckte Houston 2014 Mathematiker und
zeigte, dass für n = 6 die Regel nicht mehr funktionierte. Die Regel sagt voraus, dass 873 Episoden benötigt werden, um sechs Episoden auf jede mögliche Weise anzusehen, aber Houston hat 872 einen Weg gefunden, dies zu tun. Und da es eine einfache Möglichkeit gibt, eine kurze Superpermutation für n Zeichen in eine kurze Superpermutation für n + 1 Zeichen umzuwandeln, bedeutete das Houston-Beispiel, dass die Regel Fakultäten funktionieren nicht für alle n> 6.
Der Bau von Houston verwandelt die Aufgabe der Superpermutation in das berühmte Problem der reisenden Verkäufer, das nach dem kürzesten Weg durch mehrere Städte sucht. Insbesondere sind Superpermutationen mit dem „asymmetrischen“ Verkäuferproblem verbunden, bei dem jeder Weg zwischen zwei Städten seinen eigenen Preis hat (nicht unbedingt in beide Richtungen gleich) und das Ziel darin besteht, den günstigsten Weg durch alle Städte zu finden.
Diese Transformation ist leicht zu verstehen: Stellen Sie sich vor, dass jede Permutation eine Stadt ist, und stellen Sie sich den Weg von jeder Permutation zu jeder anderen Permutation vor. Im Superpermutationsproblem benötigen wir die kürzeste Ziffernfolge, in der alle Permutationen vorhanden sind. Unser Ziel ist es daher, alle Permutationen durchzugehen, um der anfänglichen Permutation so wenig Zahlen wie möglich hinzuzufügen. Wir geben bekannt, dass die Kosten für jeden Pfad einfach die Anzahl der Stellen sind, die wir an das Ende der ersten Permutation anhängen müssen, um die zweite zu erhalten. Im Beispiel mit n = 3 kostet der Pfad von 231 zu 312 1 USD, da wir nur 2 zum Ende von 231 addieren müssen, um 312 zu erhalten, und der Pfad von 231 zu 132 kostet 2 USD, da 32 addiert werden müssen. In einer solchen Formulierung ist dies der billigste Weg Alle Städte entsprechen direkt der kürzesten Superpermutation.
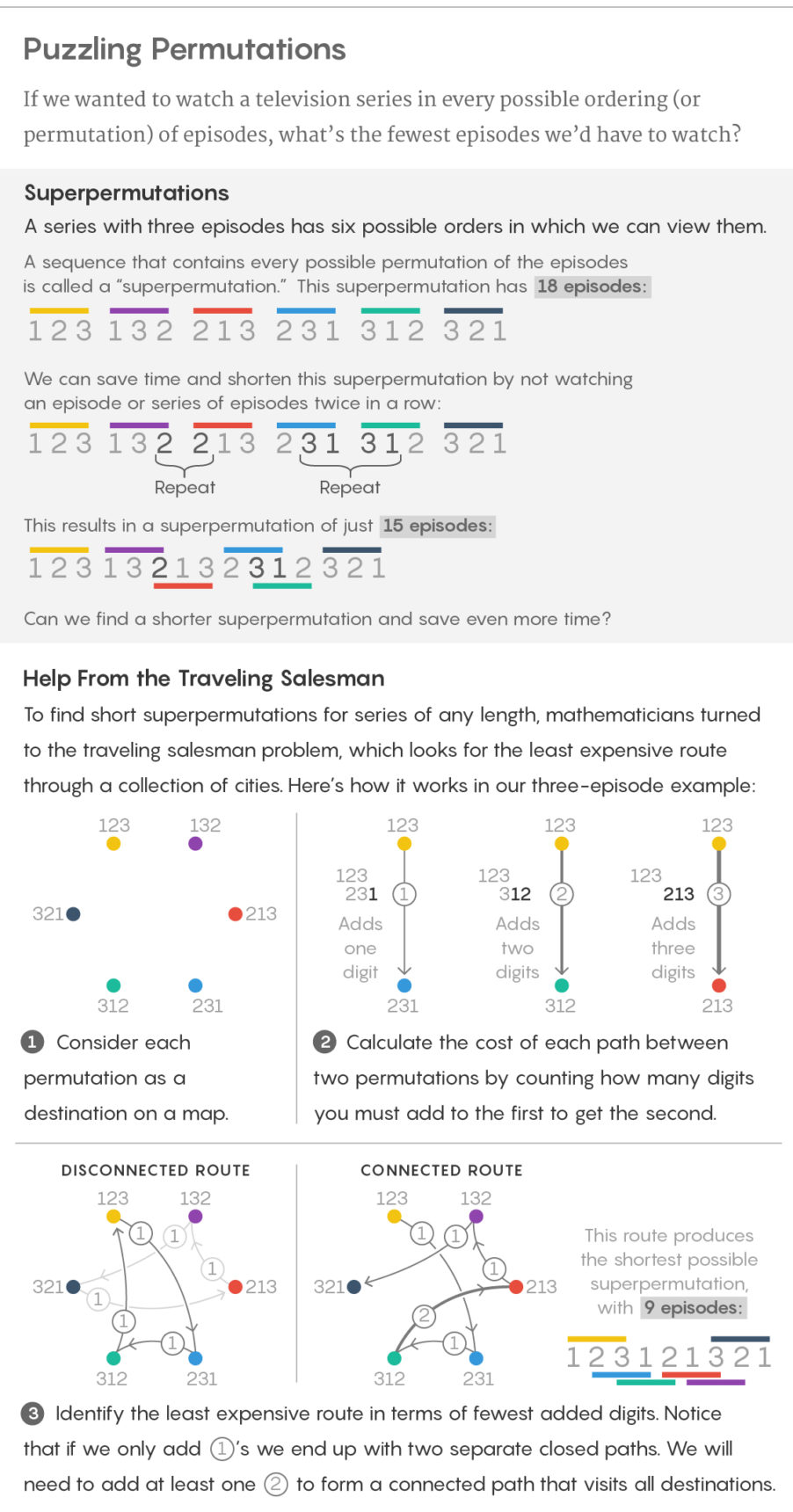
Eine solche Transformation bedeutete, dass Houston alle Fähigkeiten der Algorithmen zur Lösung des Problems der reisenden Verkäufer auf das Problem der Superpermutation lenken konnte. Dieses Problem ist bekannt für seine Zugehörigkeit zur Klasse der NP-komplexen, was das Fehlen eines effektiven Algorithmus bedeutet, der es im allgemeinen Fall lösen kann. Es gibt jedoch Algorithmen, die einige Varianten des Problems effektiv lösen können, und andere Algorithmen können gute Näherungslösungen liefern. Houston verwendete eine der letzteren, um eine Superpermutation mit einer Länge von 872 Stellen auszugeben.
Da er nur eine ungefähre Lösung angegeben hat, ist dies möglicherweise nicht einmal die idealste Superpermutation. Mathematiker führen jetzt eine umfangreiche rechnerische Suche nach der kürzesten Permutation mit 6 Zeichen durch, sagte Panton. "Wir wissen, dass unsere Suche in einer begrenzten Zeit enden wird, aber wir wissen nicht, ob es eine Woche oder eine Million Jahre dauern wird", sagte er. "Es gibt keinen Fortschrittsbalken."
Falsche Reihenfolge
Als Houstons Arbeit erschien, war ein anonymer Beitrag über 4chan fast drei Jahre lang in seiner Internetecke. Ein Mathematiker,
Nathaniel Johnston von der Mount Ellison University, bemerkte einige Tage nach Erscheinen dieses Beitrags eine Kopie dieses Beitrags auf einer anderen Website - und zwar nicht, weil er ein Anime-Liebhaber war, sondern weil er verschiedene Anfragen bei Google einging. verbunden mit Superpermutationen.
Johnston las die Beweise und es schien ihm zuverlässig, aber er verschwendete seine Energie nicht für eine gründliche Untersuchung. Zu dieser Zeit glaubten Mathematiker, dass die Fakultätsformel für Superpermutationen höchstwahrscheinlich korrekt war, und wenn Sie glauben, die genaue Antwort auf die Frage zu kennen, interessiert Sie die untere Grenze der Schätzung nicht. Mit anderen Worten, die Episoden der Serie über Superpermutationen verliefen in der falschen Reihenfolge.
Danach erwähnte Johnston die Untergrenze auf
zwei Websites , aber "Ich glaube, niemand hat dem besondere Aufmerksamkeit geschenkt", sagte er.
Dann, am 26. September 2018, twitterte der Mathematiker
John Baez von der University of California in Riverside einen
Beitrag über Houstons Entdeckung von 2014 als Teil einer Reihe von Tweets über offensichtliche mathematische Muster, die nicht mehr funktionieren.
Hinweis perev .: Es gab keine so große Serie von Tweets, nur drei. Die anderen beiden sind auch an sich interessant, obwohl sie nicht mit diesem Artikel verwandt sind. Man sagt, dass 6 der beliebteste Abstand zwischen zwei benachbarten Primzahlen für alle Primzahlen ist, die kleiner als 17.427.000.000.000.000.000.000.000.000.000 sind. Und dann funktioniert dieses Muster plötzlich nicht mehr! Die zweite zeigt die folgende Verbindung von Integralen, trigonometrischen Funktionen und der Zahl π

Aber nur für n <9,8 × 10 42 !Sein Tweet erregte die Aufmerksamkeit von Egan, der vor einigen Jahrzehnten Mathematik studierte, bevor seine Karriere als anerkannter Science-Fiction-Autor begann (seine erste erfolgreiche Geschichte hieß glücklicherweise „Die Stadt der Permutationen“). "Ich habe nie aufgehört, mich für Mathematik zu interessieren", schrieb Egan in der Mail.
Egan fragte sich, ob es möglich war, eine Superpermutation zu erzeugen, die noch kürzer war als die von Houston. Er tauchte in das Studium der Literatur ein, wie man Verknüpfungen in Permutationsnetzwerken erstellt, und fand nach einigen Wochen, was er brauchte. In ein paar Tagen folgerte er eine neue Obergrenze für die Länge der kürzesten Superpermutation von n Zeichen: n! + (n - 1)! + (n - 2)! + (n - 3)! + n - 3. Es ähnelt der Fakultätsformel, von der viele Mitglieder ausgeschlossen wurden.
"Es hat die vorherige Obergrenze vollständig überschritten", sagte Houston.
Die Untergrenze des Autors des Beitrags auf 4chan lag verführerisch nahe an der neuen Obergrenze: n! + (n - 1)! + (n - 2)! + n - 3. Nach der Veröffentlichung des Ergebnisses erinnerte Egan Johnston die Mathematiker an den Beweis eines anonymen Autors, und Houston und Panton bewiesen bald seine Richtigkeit. Wie in Houstons Arbeit eignen sich die neuen Unter- und Obergrenzen aus Sicht des Problems der reisenden Verkäufer für Superpermutationen: Die Untergrenze zeigt, dass der Pfad durch alle Städte eine Mindestanzahl von Pfaden im Wert von mehr als 1 USD durchlaufen muss, und die Obergrenze erstellt einen speziellen Pfad für jedes n. Verwenden Sie nur Verbindungen im Wert von 1 USD und 2 USD.
Jetzt versuchen Forscher, die oberen und unteren Grenzen zusammenzubringen und eine einzige Formel zu finden, die das Problem der Superpermutation löst. "Wahrscheinlich werden die Leute dieses Rätsel am Ende noch lösen", sagte Baez voraus. "Jetzt sieht alles gut aus."
Für Fans von Haruhi bietet Egans Lösung genaue Anweisungen zum Anzeigen aller möglichen Optionen für die erste Staffel mit insgesamt 93.924.230.411. Sie können heute mit dem Anschauen beginnen oder warten, bis die Mathematiker diese Zahl sogar senken können. Die Untergrenze eines anonymen Autors beweist, dass diese Kürzung nicht mehr als 40 Millionen Folgen retten wird - dies reicht jedoch aus, um sich auf die zweite Staffel vorzubereiten.