MEMS-Beschleunigungsmesser und Gyroskope - Verstehen der Spezifikationen

"Houston, wir haben Probleme", kam eine müde Stimme in meinem Gehirn und versuchte, nachts durch das InvenSense-Datenblatt IMU MPU-9250 zu gelangen. Wenn alle Wörter einzeln verständlich sind, aber ihre Beziehung mit Unmöglichkeit verwechselt wird. Alles begann mit dem LSB-Parameter, an den ich mich nur vage erinnerte, dass es sich bei der Übersetzung um das am wenigsten signifikante Bit handelte. Dann ging es zu „Auflösung“, „Empfindlichkeit“ und noch weiter wurde mir klar, dass der resultierende Text bereits den Titel „Datenblatt für Dummies“ tragen kann.

Ein wenig über die Hauptblöcke des Trägheitsmoduls.

MEMS-Gyroskop

Die MPU-9250 besteht aus drei unabhängigen einachsigen Schwingungswinkelgeschwindigkeitssensoren (MEMS-Gyroskopen), die auf eine Drehung um die X-, Y-, Z-Achse reagieren. Zwei schwebende Massen schwingen in entgegengesetzten Achsen. Mit dem Aufkommen der Winkelgeschwindigkeit bewirkt der Coriolis-Effekt eine Änderung der Schwingungsrichtung ( $$$\ vec {F} _K = -2m [\ vec {\ omega} \ times \ vec {v} _r]$ welches durch einen kapazitiven Sensor fixiert wird. Die gemessene kapazitive Differenzkomponente ist proportional zum Bewegungswinkel [Elektronikzeit]. Das resultierende Signal wird verstärkt, demoduliert und gefiltert, was zu einer Spannung führt, die proportional zur Drehgeschwindigkeit ist. Dieses Signal wird mit dem integrierten 16-Bit-ADC digitalisiert. Die Abtastrate kann programmgesteuert zwischen 3,9 und 8000 Abtastungen pro Sekunde (Abtastungen pro Sekunde, SPS) variieren, und benutzerdefinierte Tiefpassfilter (LPF) bieten einen weiten Bereich möglicher Grenzfrequenzen. Das Tiefpassfilter wird insbesondere benötigt, um Vibrationen von Motoren zu entfernen (in der Regel über 20-25 Hz).

Dreiachsiger MEMS-Beschleunigungsmesser

Verwendet für jede Achse eine separate Testmasse, die sich verschiebt, wenn entlang dieser Achse eine Beschleunigung auftritt (durch kapazitive Sensoren festgelegt). Die MPU-9250-Architektur reduziert die Exposition gegenüber Temperaturdrift und Schwankungen der elektrischen Parameter. Wenn sich das Gerät auf einer ebenen Fläche befindet, misst es 0 g entlang der X- und Y-Achse und + 1 g entlang der Z-Achse. Der Skalierungsfaktor (Skalierungsfaktor - das Verhältnis der Änderung des Ausgangssignals zur Änderung des gemessenen Ausgangssignals) ist werkseitig kalibriert und hängt nicht von der Versorgungsspannung ab. Jeder Sensor ist mit einem individuellen Sigma-Delta-ADC ausgestattet (besteht aus einem Modulator und einem digitalen Tiefpassfilter, mehr über das Gerät in [Easyelectronics]), dessen digitaler Ausgang einen einstellbaren Messbereich hat.

Und fast das dreiachsige MEMS-Magnetometer

Basierend auf hochpräziser Hall-Effekt-Technologie. Es umfasst Magnetsensoren, die die Magnetfeldstärke der Erde entlang der Achsen bestimmen, eine Steuerschaltung, eine Signalverstärkungsschaltung und eine Rechenschaltung zur Verarbeitung von Signalen von jedem Sensor. Jeder ADC hat eine Auflösung von 16 Bit, einen Messbereich $$$\ pm 4800 \ mu T$ . Zur Messung schwacher Magnetfelder wird entweder eine Einheit im Mikrotesla-SI-System (μT) oder eine Gauß-Einheit (G, GHS-System) verwendet: $$$1 G. = 100 \ mu T$ , [Funkpilot]).

Was ist LSB und wie berechnet man es? Produktionsanweisung

Nehmen wir an, unser Beschleunigungsmesser arbeitet jetzt im Messbereich $$$FS = \ pm 2g$ Das heißt, der gesamte Bereich möglicher Werte wird sein $$$2 \ cdot FS = 4g$ . Die entsprechenden Spannungswerte werden von einem 16-Bit-ADC digitalisiert, der das gesamte Intervall so weit wie möglich aufteilen kann $$$2 ^ {16} = 65536$ Schritte. Das minimale Inkrement, das erkannt werden kann, ist nur ein Schritt $$$LSB = 2 \ cdot FS / 65536$ . Hier müssen wir uns daran erinnern, dass das Konto von Grund auf neu geführt wird, so dass tatsächlich der maximale Messwert sein wird $$$2 \ cdot FS_ {true} = (2 ^ {16} - 1) * LSB = 65535 * LSB = 2 \ cdot FS - LSB$ . Das heißt, je mehr Bits in einem digitalen ADC- oder DAC-Wort enthalten sind, desto geringer ist die Diskrepanz. In diesem Fall wird die Empfindlichkeit (manchmal als Skalierungsfaktor, Empfindlichkeitsskalierungsfaktor bezeichnet) des Sensors in einem bestimmten Bereich als Verhältnis des elektrischen Ausgangssignals und der mechanischen Auswirkung bestimmt. Traditionell angezeigt für eine Signalfrequenz von 100 Hz und Temperatur $$$T = + 25 ^ {\ circ} C.$ Für die MPU-9250 beträgt die Empfindlichkeit $$$2 ^ {16} / (2 \ cdot FS)$ Schritte für jedes g oder $$$^ {\ circ} / s$ ( $$$LSB / g$ , $$$LSB / (^ {\ circ} / s)$ ), für eine andere IMU, BMI088 von Bosch Sensortec, wird die Kreiselempfindlichkeit auf die gleiche Weise berechnet und für den Beschleunigungsmesser verwendet $$$(2 ^ {16} -2 ^ 4) / (2 \ cdot FS)$ Schritte für jedes g.



Wir ziehen die FS-Varianten aus der Spezifikation für Gyroskope und, um nicht zweimal aufzustehen, Beschleunigungsmesser heraus.





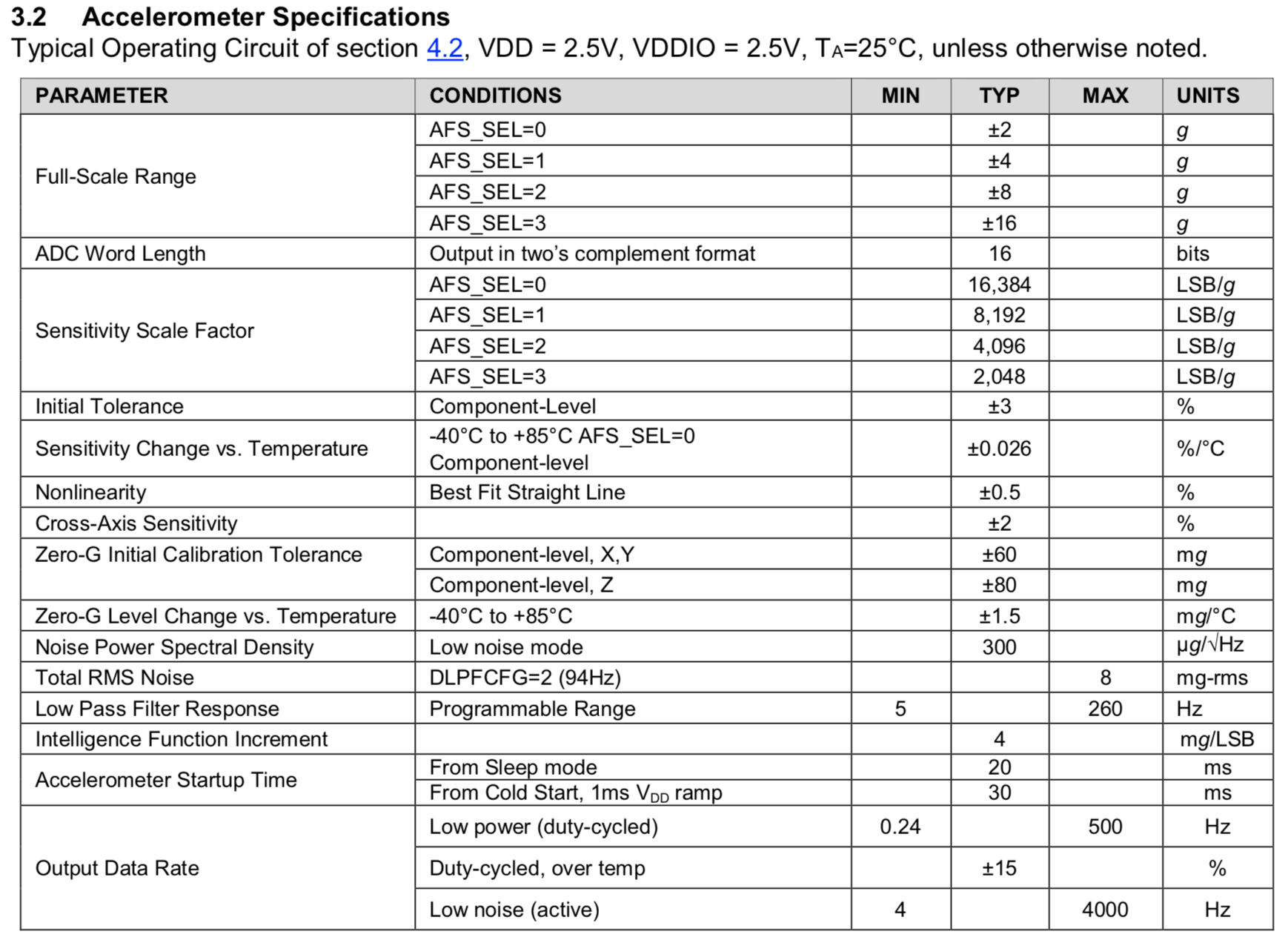
Ich habe auch FS für Beschleunigungsmesser aus der Dokumentation für BMI088 genommen (siehe unten).

Gyroskop, 16 Bit $$$(2 ^ N = 65535)$		Beschleunigungsmesser, 16 Bit $$$(2 ^ N = 65535)$
Reichweite (FS) $$$^ {\ circ} / s$ (dps)	LSB, $$$^ {\ circ} / s$ (dps)	Bereich (FS), g	LSB mg
$$$\ pm 125$ (FS = 250)	0,004	$$$\ pm 2$ (FS = 4)	0,06
$$$\ pm 250$ (FS = 500)	0,008	$$$\ pm 3$ (FS = 6)	0,09
$$$\ pm 500$ (FS = 1000)	0,0015	$$$\ pm 4$ (FS = 8)	0,12
$$$\ pm 1000$ (FS = 2000)	0,03	$$$\ pm 6$ (FS = 12)	0,18
$$$\ pm 2000$ (FS = 4000)	0,06	$$$\ pm 8$ (FS = 16)	0,24
		$$$\ pm 12$ (FS = 24)	0,37
		$$$\ pm 16$ (FS = 32)	0,48
		$$$\ pm 24$ (FS = 48)	0,73

Alles, so scheint es, ist zusammengekommen, man kann weitermachen. In einigen Fällen (unten beispielsweise ein Ausschnitt aus der Dokumentation zu BMI088) wird ein Parameter wie die Auflösung separat angegeben.

In der Tat scheint es, dass es ein LSB sein sollte. Aber warum sehen wir dann einen Wert anstelle von mehreren, die an bestimmte Bereiche gebunden sind? Ich musste die Liste der Quellen erweitern, die auf der Suche nach Antworten untersucht wurden.

Was ist Auflösung?

Der Mindestwert, den der Sensor zuverlässig erkennt, ist äußerst wichtig, wenn versucht wird, ein Gleichgewicht zwischen Preis und Leistung herzustellen. Dies ist keine Genauigkeit - ein hochauflösender Sensor ist möglicherweise nicht besonders genau, ebenso wie ein niedrigauflösender Sensor in bestimmten Bereichen möglicherweise eine ausreichende Genauigkeit aufweist. Leider definiert das LSB nur den theoretischen unterscheidbaren Mindestwert, vorausgesetzt, wir können alle 16 Bits des ADC verwenden. Dies ist eine Lösung in der digitalen Welt. In analoger Weise sind einige der Schritte verrauscht und die Anzahl der effektiven Bits ist geringer.

Was sind die Eigenschaften von Lärm und woher kommt das?

Rauschquellen können im Allgemeinen in elektronisches Rauschen einer Schaltung unterteilt werden, die Bewegung in ein Spannungssignal (Johnson-Thermorauschen, Schussrauschen, rosa 1 / f-Flimmerrauschen usw.) und mechanisch-mechanisch (Brownsch aufgrund des Vorhandenseins kleiner beweglicher Teile) umwandelt. vom Sensor selbst. Die Eigenschaften des letzteren hängen von der Resonanzfrequenz des mechanischen Teils des Systems ab $$$f_0$ (Eigenschwingungsfrequenz des Sensors $$$\ omega_0 = 2 \ pi / f_0$ )

RMS-Rauschen über den gesamten Spektralbereich - Gesamt-RMS-Rauschen (Root Mean Square)

Der Geräuschpegel kann auf verschiedene Arten bestimmt werden. Sie können sie im Zeit- oder Frequenzbereich (nach der Fourier-Transformation) berücksichtigen. Im ersten Fall wird das Restrauschen als Effektivwert der Signale vom festen Sensor verwendet (tatsächlich ist dies die Standardabweichung für die Abtastung bei $$$\ overline x = 0$ ) für einen bestimmten Zeitraum:

$$

$$x_ {RMS} = \ sigma_X = \ sqrt {\ sum_ {i = 1} ^ n {(x_i - \ overline x)} ^ 2 \ over {n-1}}$$

Beschleunigungen oder Winkeldrehzahlen, die unter dem Breitbandrauschen liegen, sind nicht zu unterscheiden - dies ist die tatsächliche Auflösung. Der Effektivwert einer Wechselspannung oder eines Wechselstroms (oft als aktiv oder effektiv bezeichnet) ist gleich dem Wert eines konstanten Signals, dessen Aktion während des Zeitraums die gleiche Arbeit in einer aktiven (ohmschen) Last ausführt. Dieser Ansatz ist am effektivsten bei der Bewertung von Breitbandrauschen, bei dem weißes Rauschen dominiert.

Für weißes Rauschen beträgt das Verhältnis von Amplitude (momentaner Spitzenwert) zu Effektivwert mit einer Wahrscheinlichkeit von 99,9% $$$N_ {PP} / N_ {RMS} = 6.6.$ Dieses Verhältnis wird als Kreuzfaktor (Crest-Faktor, Kreuzverhältnis) bezeichnet. Sie können eine Wahrscheinlichkeit von 95,5% wählen - der Kreuzfaktor beträgt 4.



Tatsächlich verhalten sich Rauschsignale nicht so gut und können Spitzen erzeugen, die den Kreuzfaktor um das Zehnfache erhöhen. In einigen Spezifikationen finden Sie die Werte $$$N_ {PP}$ oder der Multiplikator selbst.

In einem engen Niederfrequenzband von 0,1–10 Hz spielt das Flimmerrauschen „1 / f“ die Hauptrolle, das anhand der Signalamplitude von Spitze zu Spitze geschätzt wird.

Spektraldichte

Manchmal ist es bequemer, ein Signal im Frequenzbereich zu betrachten, wo seine Beschreibung als Spektrum bezeichnet wird (die Abhängigkeit von Amplitude und Phase von der Frequenz). Eine der möglichen Eigenschaften von Rauschen in den Spezifikationen wird als spektrale Leistungsdichte des Rauschens (PSD), spektrale Rauschdichte, Rauschleistungsdichte oder einfach Rauschdichte bezeichnet . Beschreibt die Verteilung der Rauschleistung über einen Frequenzbereich. Unabhängig von der Darstellung des elektrischen Signals durch Strom oder Spannung kann die an der Last abgegebene Momentanleistung normalisiert (R = 1 Ohm) und ausgedrückt werden als $$$p (t) = {\ nu} ^ 2 (t) / R = i ^ 2 (t) R = x ^ 2 (t).$ Durchschnittliche Verlustleistung des Signals über einen bestimmten Zeitraum $$$(- T / 2, T / 2),$

$$

$$P_x ^ T = \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$$

Leistung ist die Rate des Energieeintrags. Bestimmte und nichtperiodische Signale werden durch Energie bestimmt. Periodische und zufällige Signale werden als Leistung ausgedrückt, da sie nicht zeitlich und dementsprechend energetisch begrenzt sind und zu einem bestimmten Zeitpunkt ihre durchschnittliche Leistung ungleich Null ist

$$

$$P_x = \ lim_ {T \ to \ infty} \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$$

Sie können sich an [Sklyar] erinnern, dass ein beliebiges periodisches Signal durch eine Kombination einer unendlichen Anzahl von Harmonischen mit zunehmenden Frequenzen ausgedrückt wird:

$$

$$x (\ lambda) = \ frac {a_0} {2} + \ sum_ {n = 1} ^ {\ infty} (a_n \ cos n \ lambda + b_n \ sin n \ lambda),$$

das nach Darstellung des Kosinus und Sinus in Exponentialform

$$

$$\ cos \ lambda = \ frac {e ^ {i \ lambda} + e ^ {- i \ lambda}} {2}, \ sin \ lambda = \ frac {e ^ {i \ lambda} - e ^ {- i \ lambda}} {2i}$$

und Ersatz $$$\ lambda = \ omega t = 2 \ pi f_0 t = \ frac {2 \ pi t} {T_0}$ kann geschrieben werden als

$$

$$x (t) = \ frac {a_0} {2} + \ frac {1} {2} \ sum_ {n = 1} ^ {\ infty} [(a_n - ib_n) e ^ {in \ omega t} + (a_n + ib_n) e ^ {- in \ omega t}] = \ sum_ {n = - \ infty} ^ {\ infty} c_n e ^ {in \ omega t},$$

wo sind die komplexen Koeffizienten (Spektralkomponenten) der Fourier-Reihe für $$$x (t)$ ,

$$$$ display $$ \ begin {Gleichung} c_n = \ frac {1} {T_0} \ int ^ {T_0 / 2} _ {- T_0 / 2} x (t) e ^ {- in \ omega t}, dt = \ begin {Fälle} \ frac {1} {2} (a_n-ib_n), & n> 0 \\ \ frac {a_0} {2}, & n = 0 \\ \ frac {1} {2} ( a_n + ib_n), & n <0 \ Ende {Fälle} \ Ende {Gleichung} $$ Anzeige $$

Im allgemeinen Fall sind diese Koeffizienten wie folgt darstellbar:

$$

$$c_n = | c_n | e ^ {i \ theta_n},$$

$$

$$| c_n | = \ frac {1} {2} \ sqrt {a_n ^ 2 + b_n ^ 2}, \ theta_n = \ arctan \ left (\ frac {b_n} {a_n} \ right), b_0 = 0, c_0 = \ frac {a_0} {2}.$$

Amplituden- und Phasenspektrum werden als Abhängigkeitsgraphen bezeichnet. $$$| c_n |$ und $$$\ theta_n$ von der Frequenz. Leistungsspektraldichte $$$PSD (f)$ periodisches Signal $$$x (t)$ gibt die Verteilung der Signalleistung über einen Frequenzbereich an:

$$

$$PSD (f) = \ sum ^ {\ infty} _ {n = - \ infty} | c_n | ^ 2 \ delta (f-nf_0)$$

und hat Dimension $$$[W / Hz] = [x ^ 2 / Hz].$ Die durchschnittliche normalisierte Leistung des tatsächlichen Signals beträgt

$$

$$P_x = \ int ^ {\ infty} _ {- \ infty} PSD (f), df.$$

Nichtperiodische Zufallssignale (insbesondere Rauschen) können im begrenzenden Sinne als periodisch beschrieben werden. Wenn $$$T_0$ neigt zur Unendlichkeit, die Folge von Impulsen verwandelt sich in einen separaten Impuls $$$x (t)$ Wenn die Anzahl der Spektrallinien gegen unendlich tendiert, verwandelt sich der Spektraldiagramm in ein glattes Frequenzspektrum $$$X (f).$ Für diesen Grenzfall können wir ein Paar integraler Fourier-Transformationen bestimmen

$$

$$X (f) = \ int ^ {\ infty} _ {- \ infty} x (t) e ^ {- i 2 \ pi f t}, dt$$

und

$$

$$x (t) = \ int ^ {\ infty} _ {- \ infty} X (f) e ^ {i 2 \ pi f t}, df,$$

wo $$$X (f)$ - Fourierbild.

Die spektrale Leistungsdichte eines Zufallssignals wird durch die Grenze bestimmt

$$

$$PSD (f) = \ lim_ {T \ to \ infty} \ frac {1} {T} | X_T (f) | ^ 2.$$

und beschreibt die Verteilung der Signalleistung im Frequenzbereich.

Da wir davon ausgehen, dass der Durchschnitt für das weiße Rauschen der Sensoren im stationären Zustand Null ist ( $$$\ overline x = \ overline x ^ 2 = 0$ ), dann ist das Quadrat des Effektivwerts gleich der Varianz und repräsentiert die Gesamtleistung in der normalisierten Last:

$$

$$Noise_ {RMS} ^ 2 = \ sigma_x ^ 2 = P_x = \ int ^ {\ infty} _0 PSD (f), df = \ int ^ {Bandbreite} _0 PSD (f), df = PSD (Badnwidth - 0)$$

$$

$$Noise RMS = \ sqrt {Rauschdichte \ mal Bandbreite}$$

Wir schauen in die Spezifikation - dort wird tatsächlich die Quadratwurzel mit der entsprechenden Dimension unter dem Namen der Spektraldichte angegeben $$$[^ {\ circ} / s / \ sqrt {Hz}]$ oder $$$[\ mu g / \ sqrt {Hz}].$ Das heißt, der Wert des RMS-Rauschens ohne Angabe des Frequenzbandes, auf dem es gelesen wurde (Bandbreite), ist bedeutungslos.

Ein bisschen mehr über die Wahl der Bandbreite

Am Ausgang des MEMS-Sensors erhalten wir Signale mit unterschiedlichen Frequenzen. Es wird davon ausgegangen, dass wir eine bestimmte Vorstellung von den Prozessen haben, die wir im Voraus messen. Wenn beispielsweise der Beschleunigungsvektor einer Drohne bestimmt wird, ist das Geräusch die Vibration des Geräts. Sie können sie mit einem Tiefpassfilter vom Nutzsignal trennen, das alle Frequenzen über dem angegebenen Wert abschneidet (z. B. 200 Hz). Die MPU-9250 bietet die Möglichkeit, die Grenzfrequenz des Tiefpassfilters mithilfe des Parameters mit dem magischen Namen DLPFCFG anzupassen . Es steht für Digital Low Pass Filter Configuration. Weiter in der Spezifikation tauchten hier und da nicht weniger mysteriöse Ausdrücke des Typs (DLPFCFG = 2, 92 Hz) auf, aber zum Dekodieren musste ich in ein anderes Dokument klettern, "Karte und Beschreibungen registrieren". Es zeigt, welche Sätze von Bits in welche Register geschrieben werden sollten, um die gewünschten Effekte zu erzielen:



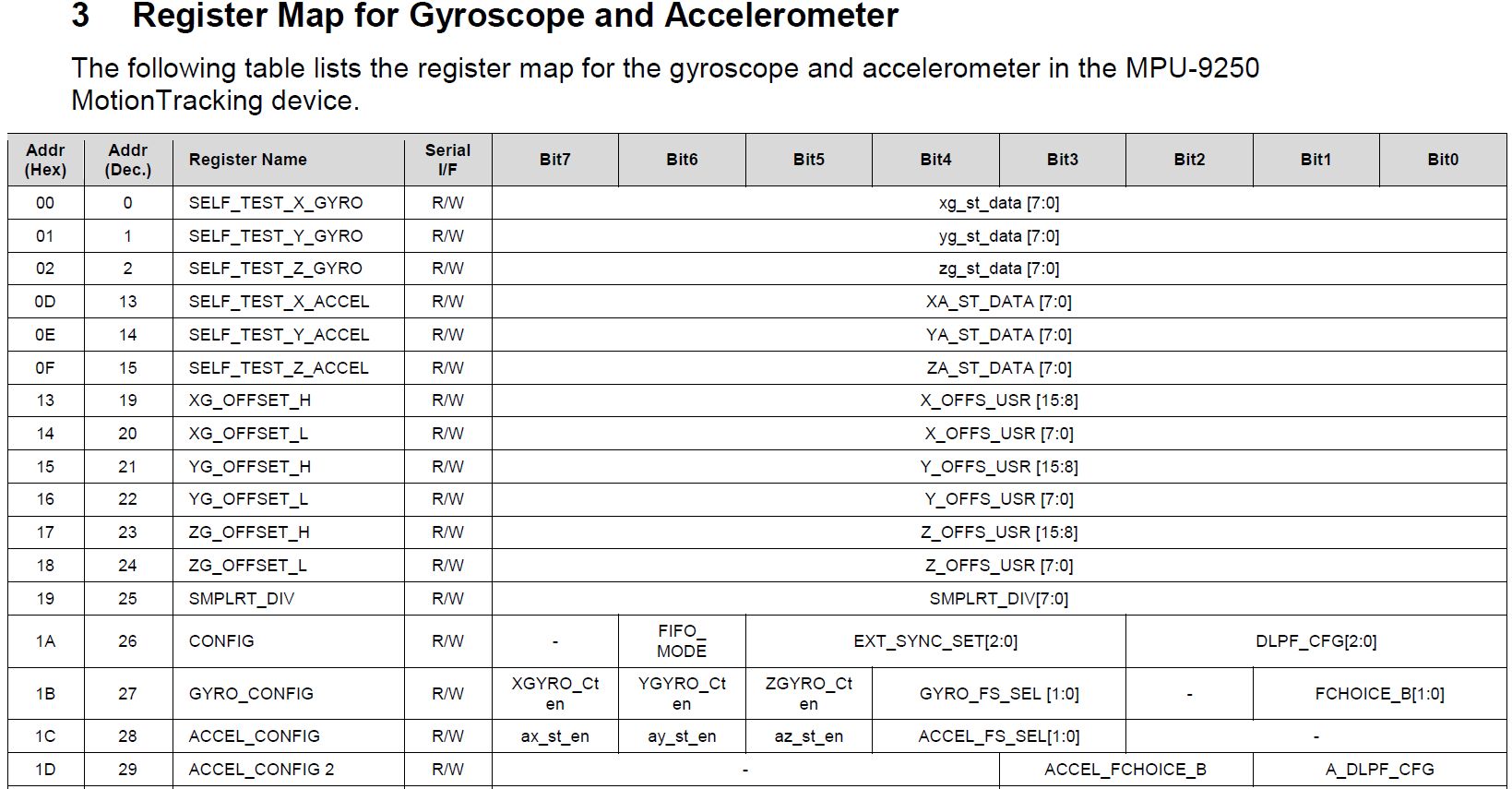
Ohne die technischen Details der Konfiguration kann Folgendes gesagt werden. Bei diesem Sensor wird eine anpassbare Filterung der Messwerte nicht nur von Beschleunigungsmessern, Gyroskopen, sondern auch des Temperatursensors durchgeführt. Für jeden gibt es insgesamt 7 bis 10 Modi, die durch Konzepte wie Bandbreite in Hz, Verzögerung in ms, Abtastfrequenz (Fs) in kHz gekennzeichnet sind.



Die Spalte "Rauschdichte" in $$$\ mu g / rtHz = \ mu g / \ sqrt {Hz}$ und die Spalte "Bandbreite" wurde mit dem Wert "3dB" ergänzt.



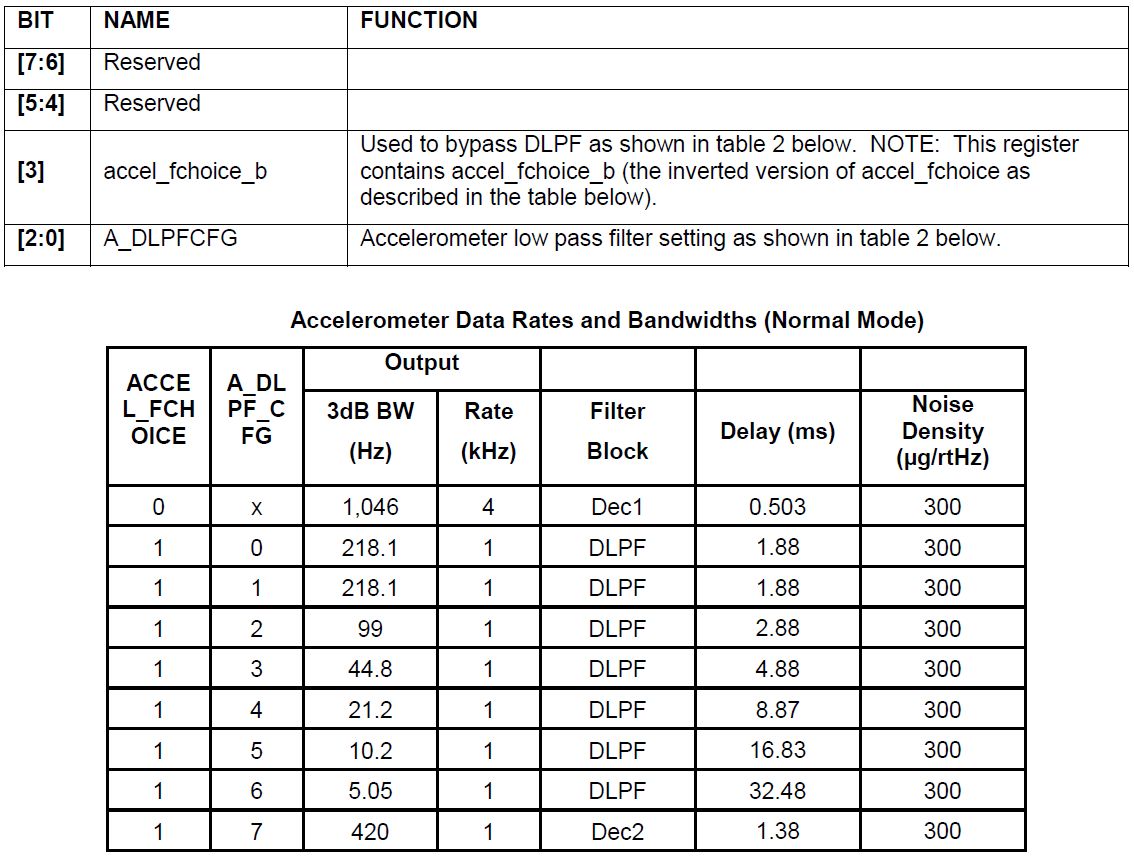
Es ist nicht einfacher, also gehen wir die Liste durch.

Vermächtnis des alten Roms

Abtastrate + Dezimierung $$$\ Delta \ Sigma$ ADC = Digital Output Data Rate (ODR)

Mit der Abtastfrequenz (es ist die Abtastfrequenz) ist alles klar - dies ist die Anzahl der Punkte eines zeitkontinuierlichen Signals, das pro Sekunde während seiner Abtastung durch den ADC aufgenommen wird. Gemessen in Hertz.

$$

$$Fs = \ frac {1} {\ delta t}$$

Um einen Wert nahe der Spitzenamplitude des Signals zu erhalten, ist es wichtig, eine Abtastfrequenz von mindestens dem Zehnfachen der Frequenz des Nutzsignals zu verwenden. Die MPU-9250 bietet drei Optionen: Fs = 32 kHz, 8 kHz, 1 kHz.

Dies bedeutet jedoch absolut nicht, dass das Signal am Ausgang des Beschleunigungsmessers oder Gyroskops mit derselben Periode erscheint.

Wenn Sie dieselben Drohnen nehmen, hängt alles vom Kampf ab, den Energieverbrauch zu senken, die Berechnungsgeschwindigkeit zu erhöhen und das Rauschen der Ausgabedaten zu reduzieren. Sie können die Häufigkeit der Aktualisierung von Ausgabedaten verringern, indem Sie internen Algorithmen erlauben, Eingabeinformationen über einen bestimmten Zeitraum zu integrieren. Der RMS-Wert nimmt ab, aber auch die Bandbreite wird schmaler (der Sensor kann nur Prozesse erkennen, deren Frequenz weniger als 50% der Datenaktualisierungsrate beträgt).

Hier ist es besser, sich sofort an Kotelnikovs Theorem zu erinnern. Sie verspricht, dass beim Abtasten eines analogen Signals ein Informationsverlust vermieden werden kann (dh um das Signal ohne Verzerrung wiederherzustellen), wenn die Frequenz des Nutzsignals nicht mehr als die Hälfte der Abtastfrequenz beträgt, die auch als Nyquist-Frequenz bezeichnet wird . In der Praxis erfordert ein klassisches Anti-Aliasing-Filter (ein Tiefpassfilter, das den Beitrag von Sekundärfrequenzkomponenten im Ausgangssignal auf vernachlässigbare Pegel reduziert - GOST R 8.714-2010) in den meisten Fällen eine Differenz von mindestens dem 2,5-fachen [Siemens].

Für Fs = 32 kHz beträgt die Nyquist-Frequenz 16 kHz. Gleichzeitig ist es unwahrscheinlich, dass ein Nutzsignal das Band fa = 20 Hz überschreitet (nur wenige können die Bewegungsrichtung mehr als 20 Mal pro Sekunde ändern). Insgesamt ist die Abtastfrequenz signifikant höher als die Frequenz, die zum Speichern der im Fa-Band enthaltenen Informationen erforderlich ist (40 Hz, 400-mal höher), dh das Nutzsignal wird überabgetastet. Das Band zwischen den Frequenzen fa und fs-fa enthält keine nützlichen Informationen. Sie können die Abtastrate reduzieren (im Diagramm wurde dies mit dem Koeffizienten M [7] durchgeführt), indem Sie die Reihenfolge der Stichproben (Stichproben) ausdünnen. Dieser Vorgang wird als Dezimierung bezeichnet .



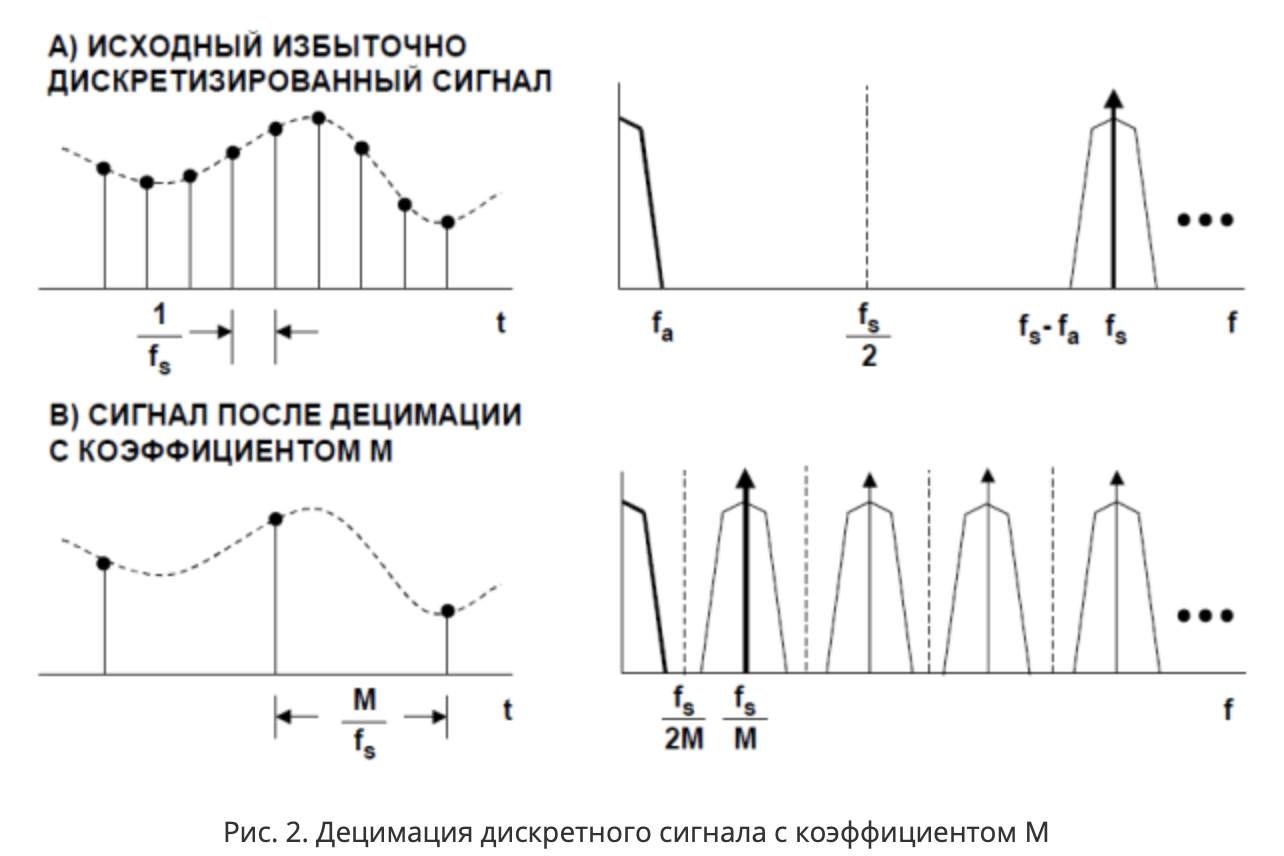
Gemäß der Spezifikation der MPU-9250 sind Beschleunigungsmesser mit einem Sigma-Delta-ADC ausgestattet . Darauf basierende Schemata verbrauchen nur minimalen Strom. Es ist zu beachten, dass die Bandbreite dieser Wandler sehr eng ist, den Schallbereich [Easyelectronics] nicht überschreitet, für einen Standard-Quadrocopter jedoch nicht mehr erforderlich ist. Sie bestehen aus zwei Blöcken: $$$\ Sigma \ Delta$ -Modulator und digitales Dezimations-Tiefpassfilter.

Warum Tiefpassfilter und Dezimierung kombinieren?

Ehrlicher Auszug aus dem Wiki:

Wenn das ursprüngliche Signal keine Frequenzen enthält, die höher als die Nyquist-Frequenz des dezimierten Signals sind, stimmt die Spektrumsform des empfangenen (dezimierten) Signals mit dem niederfrequenten Teil des Spektrums des ursprünglichen Signals überein. Die der neuen Abtastsequenz entsprechende Abtastrate ist N-mal niedriger als die Abtastfrequenz des ursprünglichen Signals.
Wenn das ursprüngliche Signal Frequenzen enthält, die höher als die Nyquist-Frequenz des dezimierten Signals sind, führt die Dezimierung zu einem Aliasing (Überlagerung von Spektren).

Um das Spektrum zu erhalten, ist es daher vor der Dezimierung erforderlich, aus den ursprünglichen Signalfrequenzen zu entfernen, die höher sind als die Nyquist-Frequenz des dezimierten Signals. Die MPU-9250-Spezifikation enthält nicht viele Informationen über die Eigenschaften von DLPF, aber Forschungen von Enthusiasten können gefunden werden [9].

Bandbreite, es ist Frequenzgang (Frequenzgang)

Der Frequenzbereich, in dem der Sensor Bewegungen erkennt und ein gültiges Ausgangssignal liefert. In einigen Spezifikationen ist der Frequenzgang des Sensors angegeben - die Abhängigkeit der elektrischen Leistung des Beschleunigungsmessers von externen mechanischen Beanspruchungen mit fester Amplitude, aber unterschiedlichen Frequenzen. Innerhalb der Bandbreite überschreitet die Ungleichmäßigkeit des Frequenzgangs keinen bestimmten Wert. Bei Verwendung eines digitalen Tiefpassfilters können Sie durch Auswahl der Bandbreite lediglich die Grenzfrequenz ändern, was sich zwangsläufig auf die Reaktionsgeschwindigkeit des Sensors bei Positionsänderungen im Raum auswirkt. Die Grenzfrequenz muss weniger als die Hälfte der digitalen Ausgangsdatenrate (ODR) betragen, die auch als Nyquist-Frequenz bezeichnet wird.

Bei MPU-9250-Beschleunigungsmessern werden die Bandbreitengrenzen so bestimmt, dass sich die spektrale Dichte des Signals innerhalb des Bereichs von der Spitze (bei einer Frequenz von 0 Hz) nicht mehr als -3 dB unterscheidet. Dieser Pegel entspricht ungefähr einem Abfall auf die Hälfte der spektralen Dichte (oder 70,7% der spektralen Spitzenamplitude). Ich möchte Sie daran erinnern, dass für Energiemengen (Leistung, Energie, Energiedichte), die proportional zu den Quadraten der Feldstärke sind, ausgedrückt in Dezibel, das Verhältnis

$$

$$D_P = 10 \ lg {P_2 \ über {P_1}}$$

.
Fazit: Die Signale, die durch das Tiefpassfilter geleitet werden, sind weniger verrauscht, haben eine bessere Auflösung, aber weniger Bandbreite. Daher ist es nicht sinnvoll, die Auflösung in der Spezifikation ohne Bezugnahme auf die Bandbreite anzugeben.

Zurück zur Auflösung

In der Spezifikation für die MPU-9250 gibt es grundsätzlich keine Informationen zur Auflösung, für den BMI088 werden unter dem Namen "Auflösung" digitale Auflösung (LSB) und Empfindlichkeit dargestellt ":



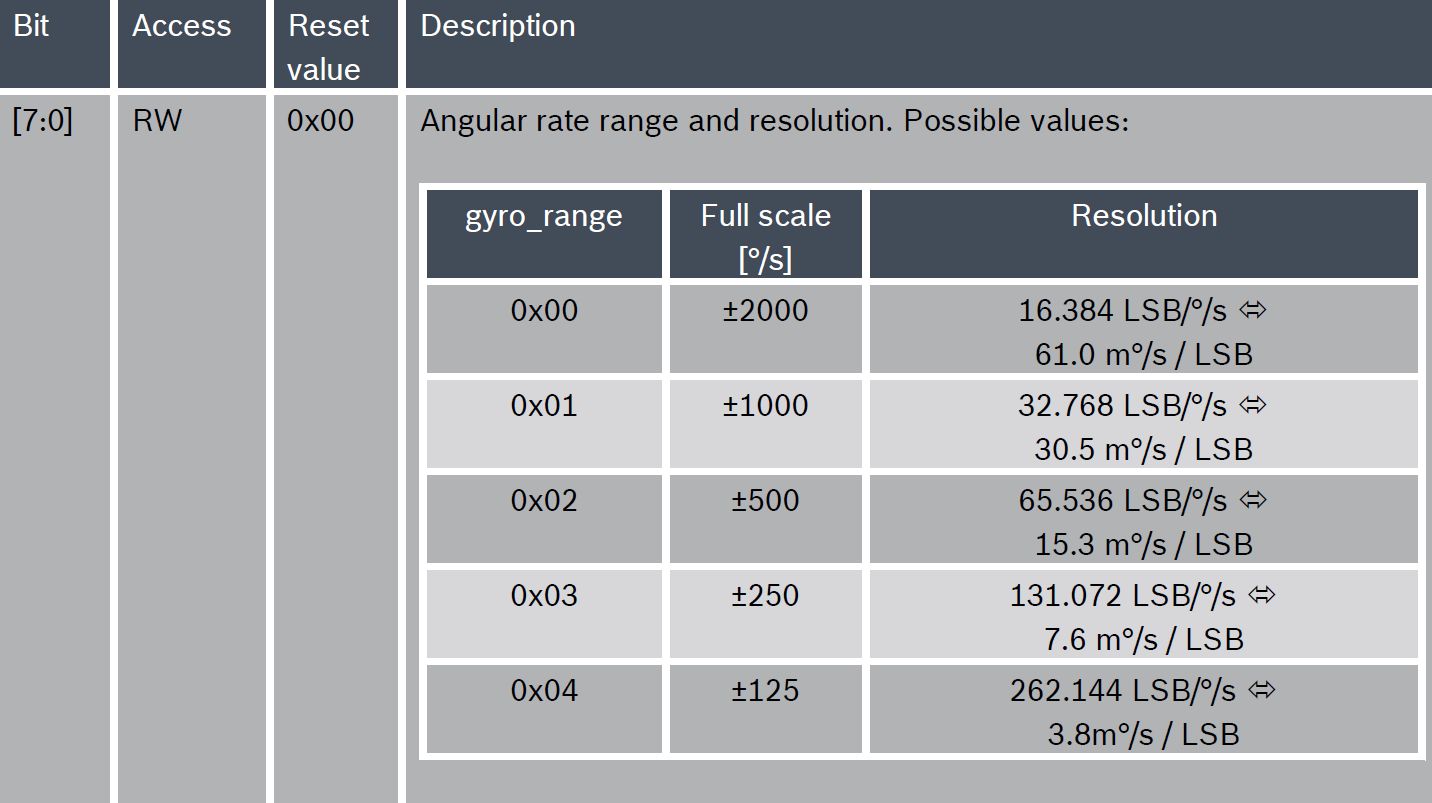
Die Auflösung für jede Bandbreite kann durch Spitzenrauschen geschätzt werden. $$$Noise_ {pk-pk} = Total Noise_ {RMS} \ times CrestFactor = Total Noise_ {RMS} \ times 4.$ Der quadratische Mittelwert des Rauschens am Ausgang bezieht sich auf die in der Spezifikation angegebene spektrale Dichte (oder besser gesagt auf die Wurzel davon) und die äquivalente Rauschbandbreite (äquivalente Rauschbandbreite, ENBW) - das Durchlassband eines äquivalenten Systems mit einem rechteckigen Frequenzgang und demselben Wert bei der Nullfrequenz wie das ursprüngliche System und die Streuung am Ausgang, wenn sie den Eingängen von Systemen mit weißem Rauschen ausgesetzt ist):

$$

$$N_ {RMS} = PSD \ times \ sqrt {ENBW}$$

Und die Rauschbandbreite ist mit dem 3dB-Band durch Koeffizienten verbunden, die der Reihenfolge des Tiefpassfilters entsprechen:

$$

$$ENBW = 1.57 \ cdot f_ {3dB} \ textrm {für 1. Ordnung}$$

$$

$$ENBW = 1.11 \ cdot f_ {3dB} \ textrm {für 2. Ordnung}$$

$$

$$ENBW = 1.05 \ cdot f_ {3dB} \ textrm {für 3. Ordnung}$$

$$

$$ENBW = 1.025 \ cdot f_ {3dB} \ textrm {für 4. Ordnung}$$

Nach der Studie in [MPU9250_DLPF] haben wir eine Wahl von 1,57. Der erhaltene Effektivwert berücksichtigt den Beitrag des weißen Rauschens (dort gibt es kein Quantisierungsrauschen oder mechanisches Rauschen). Zum Beispiel für den Beschleunigungsmesser der berechnete Wert für $$$BW = 99 Hz, PSD = 300 \ mu g / \ sqrt {Hz}$ es stellt sich heraus $$$N_ {RMS} = 4 mg$ . In diesem Fall enthält die Spezifikation das gesamte Effektivrauschen $$$Total RMS Noise = 8 mg.$ Die Diskrepanz ist signifikant. Leider ist es nur für ein Band angegeben, und für den BMI088-Beschleunigungsmesser ist in der Spezifikation nur PSD angegeben. Also werden wir verwenden, was ist. Nehmen Sie den Kreuzfaktor 4. Jetzt der interessanteste. Haltung $$$FS / Noise_ {pk-pk}$ gibt eine ungefähre Reihenfolge der effektiven Bits in diesem Messbereich an, die deutlich unter der 16-Bit-Auflösung des ADC liegt.

MPU-9250			BMI088
Gyroskop
$$$\ small N ^ {Total} _ {RMS} = 0,1 ^ {\ circ} / s (BW = 92 Hz)$			$$$\ small N_ {RMS} = 0,1 ^ {\ circ} / s (BW = 47 Hz)$
$$$\ small PSD = 0,01 ^ {\ circ} / s / \ sqrt {Hz}$			$$$\ small PSD = 0.014 ^ {\ circ} / s / \ sqrt {Hz}$
$$$\ small BW, Hz$	$$$\ small N_ {RMS}, ^ {\ circ} / s-rms$	$$$\ small N_ {PP}, ^ {\ circ} / s$	$$$\ small BW, Hz$	$$$\ small N_ {RMS}, ^ {\ circ} / s$	$$$\ small N_ {PP}, ^ {\ circ} / s$
			523	0,41	1.6
250	0,2	0,8	230	0,27	1.1
184	0,17	0,69	116	0,19	0,76
92	0,12	0,49	64	0,14	0,57
41	0,08	0,32	47	0,12	0,49
20	0,06	0,23	32	0,1	0,4
10	0,04	0,16	23	0,09	0,34
5	0,03	0,11	12	0,06	0,25
Beschleunigungsmesser
$$$\ small N ^ {Total} _ {RMS} = 8 mg \ textrm {(BW = 99 Hz)}$			$$$\ small PSD_ {XY} = 160 \ mu g / \ sqrt {Hz}$
$$$\ small PSD = 300 \ mu g / \ sqrt {Hz} \ textrm {(Gyro off)}$			$$$\ small PSD_Z = 190 \ mu g / \ sqrt {Hz} (g_ {FS3g}, \ textrm {Normalmodus})$
$$$\ small BW, Hz$	$$$\ small N_ {RMS}, mg$	$$$\ small N_ {PP}, mg$	$$$\ small BW, Hz$	$$$\ small N_ {RMS_XY}, mg$	$$$\ small N_ {PP_XY}, mg$
218.1	5.6	22	280	3.4	14
99	3.8	15	145	2.4	10
44.8	2.5	10	80	1.8	7
21.2	1.7	7	40	1.3	5
10.2	1.2	4.9	20	0,9	4
5.05	0,9	3.4	10	0,6	2.6
420	7.8	31	5	0,5	1.8
1046	12.3	49

Verzögerung (ms) oder woher kommt die Verzögerung?

Aufgrund der Notwendigkeit, Variablen im internen Puffer zu speichern, um das Signal durch das Filter bei verschiedenen Frequenzen zu teilen

Insgesamt Je niedriger die Grenzfrequenz des Filters ist, desto weniger Rauschen im Signal. Aber hier müssen wir vorsichtig sein, denn gleichzeitig wächst die Verzögerung. Außerdem können Sie das Nutzsignal überspringen [8].

MPU-9250		BMI088
Gyroskop, 16 Bit
Reichweite (FS) $$$^ {\ circ} / s$ (dps)	Auflösung, Bit (BW = 92 Hz)	Reichweite (FS) $$$^ {\ circ} / s$ (dps)	Auflösung, Bit (BW = 64Hz)
		$$$\ pm 125$	8
$$$\ pm 250$	9	$$$\ pm 250$	9
$$$\ pm 500$	10	$$$\ pm 500$	10
$$$\ pm 1000$	11	$$$\ pm 1000$	11
$$$\ pm 2000$	12	$$$\ pm 2000$	12
Beschleunigungsmesser
Bereich (FS), g	Auflösung, Bit $$$(N_ {PP} = 32 mg)$	Bereich (FS), g	Auflösung (X, Y), Bit $$$(N_ {PP} ^ XY = 14 mg)$
$$$\ pm 2$	6	$$$\ pm 3$	8
$$$\ pm 4$	7	$$$\ pm 6$	9
$$$\ pm 8$	8	$$$\ pm 12$	10
$$$\ pm 16$	9	$$$\ pm 24$	11

Und dies sind nur die grundlegendsten Parameter.

Woher kam das:

1. Das unterhaltsamste Dokument von Freescale Semiconductor ist "Wie viele Bits sind genug?"
2. [EE] - "Auflösung gegen Genauigkeit gegen Empfindlichkeit, die die Verwirrung durchschneidet"
3. [Elektronikzeit] - „MEMS-Bewegungssensoren von STMicroelectronics: Beschleunigungsmesser und Gyroskope“
4. [LSB] - "Ein ADC und DAC Least Significant Bit (LSB)"
5. [Measurement Computing] - „TechTip: Genauigkeit, Präzision, Auflösung und Empfindlichkeit“
6. [KIT] - "Beschleunigungsmesser für analoge Geräte - Gerät und Anwendung"
7. [Easyelectronics] - "Sigma-Delta ADC"
8. [Radiolotsman] - "Magnetometer: Funktionsprinzip, Fehlerkompensation"
9. [SO] - "Rauschmessung"
10. [Mide] - "Beschleunigungsmesserspezifikationen: Entschlüsseln des Datenblatts eines Beschleunigungsmessers"
11. [CiberLeninka] - Delta-Sigma ADC-Filter
12. [SciEd] - "Merkmale der Implementierung der digitalen Filterung mit einer Änderung der Abtastfrequenz"
13. [MPU6050] - „Verwenden des DLPF der MPU6050“
14. [MPU9250_DLPF] - MPU9250 Gyro Noise DLPF-Arbeitsuntersuchung
15. Grundlegendes zu den Spezifikationen für die Sensorauflösung
16. Digitale Signalverarbeitung von Siemens
17. MEMS-Bewegungssensoren von STMicroelectronics
18. [TMWorld] - "Auswertung von Trägheitsmesseinheiten"
19. [Sklyar] - Sklyar B. Digitale Kommunikation. Theoretische Grundlagen und praktische Anwendung.